Тевяшев А.Д., Литвин О.Г. Вища математика у прикладах та задачах. Ч 1
Подождите немного. Документ загружается.


§3.
Системи лінійних алгебраїчних рівнянь
Метод повного виключення може бути використаний для обернення мат-
риць (відомий також під назвою метод елементарних перетворень). Для даної
матриці А п -го порядку будується прямокутна матриця {а
|
е) розміру п х 2п ,
до якої застосовуються перетворення за алгоритмом повного виключення , в
результаті чого матриця зводиться до вигляду (£| в), де В = А~
1
. Це завжди
можливо, якщо матриця А невироджена.
//. Контрольні питання та завдання
1.
Яка система рівнянь називається лінійною?
2.
Що називається основною матрицею системи та розшире-
ною матрицею?
3.
Сформулюйте теорему Кронекера-Капеллі - критерій су-
місності системи.
4.
В якому випадку система лінійних рівнянь має єдиний роз-
в'язок; безліч розв'язків; не має розв'язків?
5.
Які невідомі сумісної системи лінійних рівнянь назива-
ються базисними, які - вільними?
6. Скільки базисних невідомих має система; скільки вільних
невідомих має система?
7.
Яка система лінійних рівнянь називається однорідною?
8. Сформулюйте критерій нетривіальної розв'язності од-
норідної системи лінійних рівнянь.
9. Що називається фундаментальною системою розв'язків
лінійної системи однорідних рівнянь?
10.
Запишіть структуру загального розв'язку однорідної сис-
теми лінійних рівнянь; неоднорідної.
11.
Викладіть матричний метод розв'язання невироджених
систем лінійних рівнянь.
12.
Викладіть правило Крамера розв'язання невироджених
систем лінійних рівнянь.
13.
Викладіть метод Гаусса розв'язання систем лінійних рівнянь.
14.
Викладіть метод Жордана - Гаусса (метод повного вик-
лючення) розв'язання систем лінійних рівнянь.

1
1
2 Глава 3. Визі і а чники та матриці. Системи лінійних алгебраїчних рівнянь
///. Приклади розв'язання задач
Приклад 1. Записати в матричному вигляді систему рівнянь:
Зх] + 2х
2
- х
3
= 1;
Х| "Ь х
3
х^
—
2 і
2х| -і
-
2х
2
~""
Зх
3
х^
—
5 .
• Для даної системи
або
А =
3 2-1 0
10 1-1
2 2 3 -І
X
X,
х
2
х
3
\
х
4у
ч5у
Отже, в матричному вигляді система запишеться так:
АХ = В
3 2-10
10 1-1
2 2 3 -1
( г >
X]
ґ-1
х
2
_
2
,5; ,5;
Приклад 2. Розв'язати задану систему трьома методами:
1) матричним методом; 2) за формулами Крамера; 3) методом
Гаусса:
З.ї] + 2х
2
~
х
3
= _
3 '
2х) - х
2
+ 2х
3
= 11;
-Х\ + Зх
2
+ х
3
= 0.
• 1. Розв'язання системи матричним методом
Запишемо систему рівнянь у вигляді матричного рівняння А X = В, де
' 3
2 -]Л
'
_3
1
А =
2 -1 2
5 =
11
,-1
з
і,

§3.
Системи лінійних алгебраїчних рівнянь 113
Із матричного рівняння АХ = В
=>
X = А~ В .
Розв'язок матричним методом можливий, якщо с!еі А = А * 0
,
тобто якщо
матриця А невироджена:
3 2-1
0 11 2
А =
2-12
=
0 5 4
= (-1)
-1 3 1
-1 3 1
11 2
5 4
= -(44-10) = -34*0,
тобто існує єдина обернена матриця, отже, і єдиний розв'язок системи.
Знайдемо обернену матрицю Л
-1
:
11
А
2\
Азі
12
А
32
13
А
23 А 33
де Ау=(-\)'
+
>-М
І;
, 1 < г, У < 3 .
Знайдемо алгебраїчні доповнення
А,,
=
Ац -
А
ЗІ
=
-1 2
З 1
2 -1
3 1
2 -1
-1 2
= -7,
= -5
= 3 .
42
і
22
•
Л32 = '
2 2
-1 1
3 -1
-1 1
З -1
2 2
= -Л.
= 2.
•із
*23
2 -1
-1 З
З 2
-1 З
= 5;
=
-11;
^зз -
З 2
2 -1
= -7:
Г-7 -5 З'
-4 2 -8
. 5 -11 -7,
Перевіримо правильність знаходження оберненої матриці шляхом пере-
А~
1
=-±
34
вірки виконання рівності А.
= Е:
АА~
=
2 -1
-1 2
3 1
34
-7
-4
5
-5 3^
2 -8
•11 -7,
34
'-34
0
о
4
'1
0 0^
0
-34
0
=
0 1 0
= Е
0
-34,
,0 0
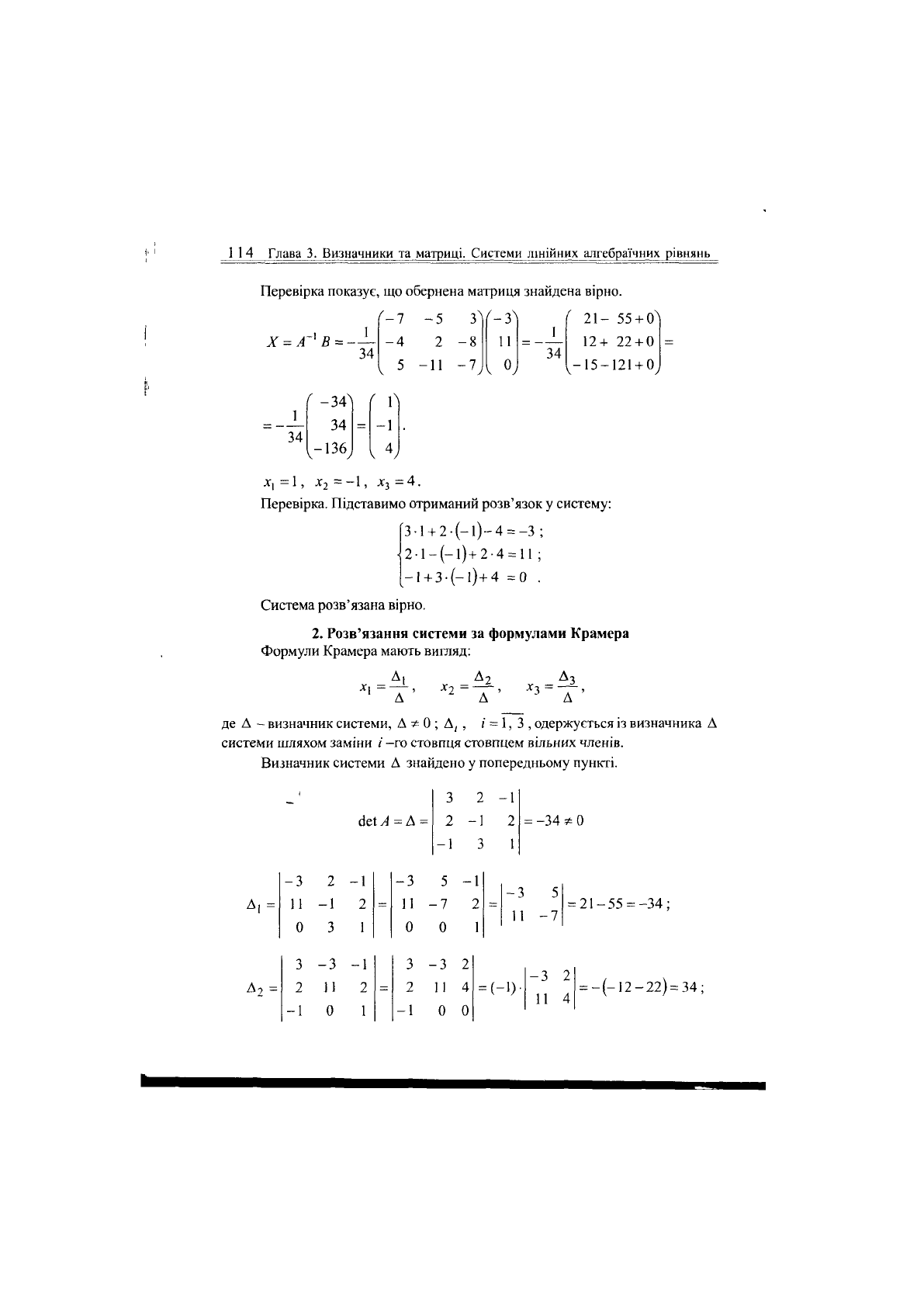
1
1
4 Глава 3. Визначники та матриці. Системи лінійних алгебраїчних рівнянь
Перевірка показує, що обернена матриця знайдена вірно.
34
(-1
-5
3
)
/
~
3
1
(
21
-
55 + 0'
-4
2
-8 11
І
12
+
22 + 0
~~34
, 5
-11
-ь
V
°,
,-15-
121
+ 0,
( -34^ ( \\
34
=
-1
,"136,
, \
х
2
=-
1,
х
3
=
___\_
34
Х\ =1,
Перевірка. Підставимо отриманий розв'язок у систему:
З
-1
+ 2
-
(-1)-4
= -3 ;
• 2-1-(-і)+2-4 = 11 ;
-1 + 3-(-і)+4 =0 .
Система розв'язана вірно.
2.
Розв'язання системи за формулами Крамера
Формули Крамера мають вигляд:
_Д,
_А2_ _Д
І
Х,_
Т'
Х2
"а'
ХЗ
~Д'
де А - визначник системи, А * 0 ; А, , і
—
1, 3 , одержується із визначника А
системи шляхом заміни / -го стовпця стовпцем вільних членів.
Визначник системи А знайдено у попередньому пункті.
дсіА = А =
3 2-1
2-12
-1 3 1
-34*0
-3
2 -1 -3
5 -
1
11
-1 2
=
11
-7
2
=
0 3 1
0
0
1
3 -3 -1 3 -3
2
А
2
= 2 11 2
=
2
11
4
=
(-
-1
0 1
-1
0 0
-З 2
11 4
•55 = -34:
= -(-12-22) = 34;
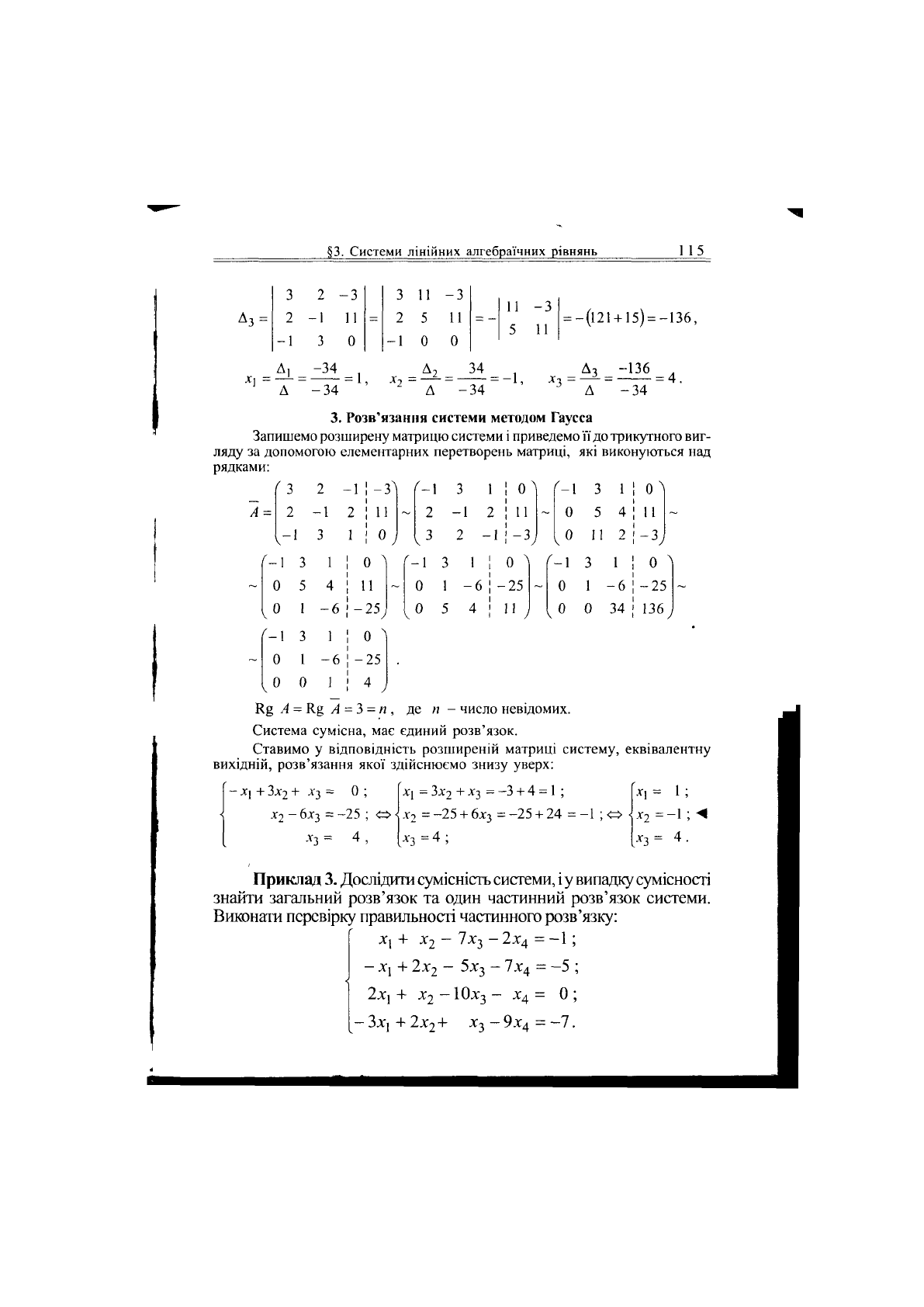
§3, Системи лінійних алгебраїчних рівнянь 115
3 2 -3 3 11
-3
2
-1 11 =
2
5
11
-1
3 0
-1
0
0
-
34
=1,
-34
Д
-
34
=1,
-34
х
2
Д
-
11
= —(121 + 15)=—136,
34
Ді
-136
-34
= 4.
3.
Розв'язання системи методом Гаусса
Запишемо розширену матрицю системи і приведемо її до трикутного виг-
ляду за допомогою елементарних перетворень матриці, які виконуються над
рядками:
-1 ! -3
Л
Гз
2
V"
-1
•1 З
о
1
4
-6
1
-6
2 ! 11
і
і о
о
^
11
25
0
25
4
)
Г-1
3 1
! о '-1
3
1
°1
2 -1 2
і її
~
0 5
4
11
2 -1
і
-з
) V
0
11 2
-з,
ґ _
-1
3
і ! 0 ^
ґ
-1
3
1
0
0
1
-6
і
-25
0
1 -6
-25
V
0 5
4 ;
Ч )
0 0
34
136
)
К§ А = К§ А = 3 = п , де п
—
число невідомих.
Система сумісна, має єдиний розв'язок.
Ставимо у відповідність розширеній матриці систему, еквівалентну
вихідній, розв'язання якої здійснюємо знизу уверх:
-
Х\
+ 3x2 +
х
5
=
0 ;
х
2
- 6x3 = -25 ; <=>
х
3
= 4,
Хі = Зх
2
+ х
3
=-3 + 4 =
1
;
х
2
=-25+ 6х
3
=-25 + 24
=
х
3
= 4 ;
-1 ;о
X] =
1
;
х
2
=-1;<
х
3
= 4.
Приклад
3.
Дослідити сумісність
системи,
і у випадку сумісності
знайти загальний розв'язок та один частинний розв'язок системи.
Виконати перевірку правильності частинного розв'язку:
х, + х
2
- 7х
3
•
•
Х^
"4" ^"^3
2х
4
=
-1;
- 7х
4
=:
—5
;
2х] + х
2
- Юх
3
- х
4
= 0 ;
•Зхі+2х
2
+ х
3
-9х
4
=-7.

1
1
6 Глава 3. Визначники та матриці. Системи лінійних алгебраїчних рівнянь
• Запишемо розширену матрицю системи і за допомогою елементарних
перетворень, що виконуються над рядками матриці, зведемо її до східчастого
вигляду:
( 1
1
-7
-2 !
-Г|
ґ
\ 1 - 7 2
!
~м
-1 2 -5
-7
-5
0 3
-12
•9
!
-6
2 1 -10 -1 0 0 -1 4
3
1
2
2
1
-9 |
5
-20 -
15
і -
-10,
ґ
1 1
-7
-2
-г
(\
1
„7 _
2
-г
0
1
-4
-3
-2
0 1
_4 _
3 | -
2
0
1
-4
-3
-2
0 0 0 0
0
,о
1
-4
-3
-2,
,0
0
0
0
[
0;
Отримали:
К§ А =
К§,
А = г = 2<4 = п, л - число змінних. Згідно з теоремою
Кронекера - Капеллі система сумісна; система має безліч розв'язків, бо
г <п . Розв'язання здійснюємо методом Гаусса. Базисні змінні - х\, х
2
;
вільні змінні - х
3
, х
4
.
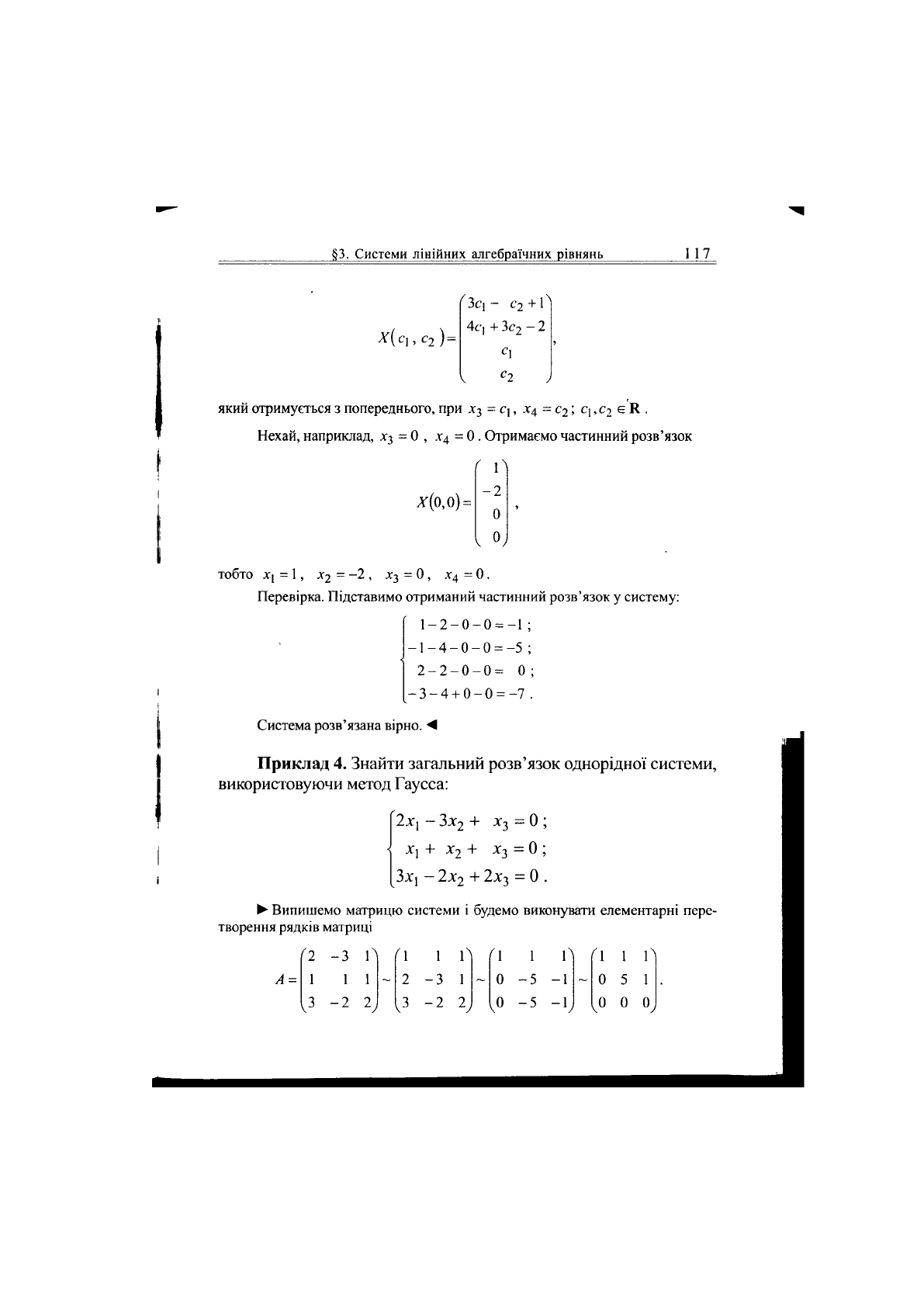
Ставимо у відповідність перетвореній розширеній матриці системи
скорочену систему, яку розв'язуємо знизу уверх:
|х[ + х
2
- 7х
3
-2x4 =
_
1 ; \
х
\
+
х
2
=
7
х
з
+
2*4 ~
1 »
х
2
- 4х
3
- Зх
4
= -
2
,
х
2
= 4х
3
+ Зх
4
- 2 ,
X] = -х
2
+ 7х
3
+ 2x4 ~
1
=
~4х
3
- Зх
4
+ 2 + 7х
3
+ 2x4
_
1
'>
х
2
=
4х
3
+ Зх
4
- 2 ,
де х
3
, х
4
є К , або у вигляді
§3.
Системи лінійних алгебраїчних рівнянь 117
Х{с
и
с
2
) =
(Зс
{
- с
2
+\
л
4с,
+ Зс
2
- 2
с
\
сі
ЯКИЙ ОТРИМУЄТЬСЯ 3 ПОПЕРЕДНЬОГО, ПРИ Х
3
= С), Х
4
= С
2
; С], с
2
Є К .
Нехай, НАПРИКЛАД, х
3
= 0 , х
4
= 0. Отримаємо ЧАСТИННИЙ РОЗВ'ЯЗОК
ЛЧ0,0) =
тобто
X]
= 1, х
2
= -2, х
3
= 0, х
4
= 0.
Перевірка. Підставимо отриманий частинний розв'язок у систему:
1-2-0-0
= -1;
-1-4-0-0 = -5 ;
2-2-0-0= 0;
-3-4 + 0-0 = -7 .
Система розв'язана вірно. -4
Приклад 4. Знайти загальний розв'язок однорідної системи,
використовуючи метод Гаусса:
2х, -
Зх->
+ 0
Х\ + х
2
+ х
3
= 0 ;
Зх] - 2х
2
+ 2х
3
= 0 .
• Випишемо матрицю системи і будемо виконувати елементарні пере-
творення рядків матриці
(2
-3
п
Ґ1
1
г
Ґ1
1 0
і Г
А =
1 1 1
~
2
-3
1
~ 0 -5
-1
~
0 5 1
,з
-2
2,
,з
-2
2,
-5 0 0
у

118 Глава 3. Визначники та матриці. Системи лінійних алгебраїчних рівнянь
К&А = г = 2<п = 3, п - число невідомих. Система має нетривіальні
1 1
розв'язки. Базисний мінор
0 5
Ставимо у відповідність матриці спрощену систему:
{
х
\ +
х
2
+
х
3
=
0
>
5х
2
+ х
3
= 0 ,
де х\, х
2
- базисні змінні, х
3
- вільна змінна;
Х
\+х
2
=
—х$
;
5х
2 = ~*3 >
х
3
А
х, --х
3
+ — -- — х
3
;
Х2
~ 5 '
Загальний розв'язок: х
х
=-ух
3
,
х
2
=
~~~^~>
х
з
є
^-
Якщо перепозначити вільну змінну х
3
= с, отримаємо загальний розв'я-
зок у вигляді
'-Ас
15"
Х
Х= -с/5 УсєК.
,
с
,
Підставивши отриманий розв'язок у систему, переконаємося у правиль-
ності отриманого розв'язку.
Приклад 5. Дослідити, чи має нетривіальні розв'язки одно-
рідна система рівнянь. У випадку позитивної відповіді, знайти її
загальний розв'язок. Записати також фундаментальну систему роз-
в'язків.
Х[ + 2х
2
+ 4*3 - Зх
4
= 0 ;
ЗдГ] + 5х
2
+ 6х
3
- 4х
4
= 0 ;
4*і + 5х
2
- 2х
3
+ Зх
4
= 0 ;
Зх, + 8х
2
+ 24х
3
- \9х
4
= 0 .

<=>
ґ
\
2 4
~
3
]
'1 2 4
-
3^
Гі
2 4
~
3
)
3
5
6
-
4
0 -1
-6
5 0 -1
-6
5
—
4 5 -2
3
0
-3
-18 15 0 0 0 0
,з
8 24
-19,
,о
2 12
-іо;
,0
0 0
К$А = г = 2<п = 4 ,система має нетривіальні розв'язки.
2
Базисний мінор
.
Базисні змінні - х
х
, х
2
; вільні змінні - х
3
, х
4
.
0
-1
Скорочена система має вигляд:
\х\+ 2х
2
+
4х
3 ~ 3*4 =0 \х\+ 2х
2
=
-4хз + 3*4
|
-х
2
-6х
3
+ 5*4 =0 |х
2
=
-6х
3
+ 5х
4
\х\ = -4х
3
+ Зх
4
-
2(-6х
3
+ 5х
4
) = -4хз + Зх
4
+12х
3
- 10х
4
= 8х
3
- 7х
4
|х
2
= -6х
3
+ 5х
4
X] —
8х
3
—
7х
4
[х
2
= -6х
3
+5х
4
.
Загальний розв язок: х,
—
8х
3
—
7x4,
х
2
—
—6х
3
+ 5х
4
, Х3, х
4
є К .
Перепозначимо змінні х
3
=
С],
х
4
= с
2
.
Загальний розв'язок запишемо у вигляді:
Х(
С]
,с
2
) =
8с,
-7с
2
^
- 6с[
+ 5с
2
С
1
с
2
\/С],с
2
є К.
Поклавши
С]
= 1, с
2
= 0 та
С)
= 0, с
2
= 1, з загального розв'язку одер-
жуємо фундаментальну систему розв'язків:
Е
1
=Х(\,0) =
Е
2
=Х{0,\) =
Таким чином, фундаментальна система розв'язків:
{(8,-6,1,0),(-7,5,0,1)}.^

120 Глава 3. Визначники та матриці. Системи лінійних алгебраїчних рівнянь
Приклад
6.
Дослідити систему на сумісність та знайти її загаль-
ний розв'язок методом Жордана-Гаусса (повного виключення).
X] + 2х
2
+ Зх
ЗХ|
~ь
2х
2
~ь
х
3
х^
—
1
х
4
= 1
2х, + Зх
2
+ х
3
+ х
4
= 1
= 2.
• Скористаємося алгоритмом методу повного виключення:
А =
ГИ
2 3 -1
(\
2 3
-1
п
(
-4
0
4
0
°1
3
2
1
-1
і
о,
-4|
- 8
2
-2 0 -4
-8 2 -2
2 3
1 1
і
0
-] - 5 3
-1 0 0 12
-10
2
,
5
5
2 0
2
)
1°
-5
-13
5
1
0
0 12
-10
2
,
10-1 о
0 2 4 -1
0
0 І6
6 0 0 -5
0 12 0 14
0 0 6 -5
К\уА
= К§,А = 3<4 =
п,
система сумісна, має безліч розв'язків.
• Поставимо у відповідність матриці А спрощену систему рівнянь. Вва-
жатимемо,
X],
х
2
, хз - базисні змінні, х
4
- вільна змінна.
6х) - 5х
4
= 1
12х
2
+ 14х
4
= 2
6х
3
- 5х
4
= 1
6х) =
1
+ 5х
4
;
6х
2
=
1
- 7х
4
;
6х
3
=
1
+ 5х
4
,
Загальний розв'язок системи представиться так:
(\
5
6
+—х
4
6
4
1
7
6
~6*
4
1
5
6
+ —Хд
6
4
V
х
4
х
4
є К .
1
+ 5х
4
1-7*4
Х2=
~Т"'
1
+ 5х
4
х
3
= —-— .
