Владимирский С.Р. Механизация строительства мостов
Подождите немного. Документ загружается.

Вибромолоты характеризуются теми же параметрами, что и вибропогружатели, а
также энергией и частотой ударов.
Энергия удара (Дж)
E = mv
2
/ [2(l-R)], (22)
где m — масса ударной части молота, кг; v — ударная скорость вибромолота, м/с (v ≤
2 м/с); R — условный коэффициент восстановления скорости при ударе (-1 ≤ R ≤ +1).
За рубежом выпускают вибромолоты (как навесное оборудование к гидравлическим
экскаваторам) с электроприводом (модель РЕ26.02) и с гидроприводом (модель
HVB40/26). Характеристики названных моделей приведены в табл. 16.
Гидровибромолоты более компактны, не потребляют электроэнергии, но менее мощные.
Погружение и извлечение шпунта вибромолотами связаны с неизбежными
сотрясениями грунта, которые крайне нежелательны по экологическим соображениям и
недопустимы при работе вблизи существующих сооружений. Гидравлический агрегат
Tiewood английской фирмы BSP работает почти бесшумно, используя принцип
статического группового задавливания металлических шпунтовых свай (рис. 31). Длина
хода штоков гидродомкратов — 0,75 м.
Эффективным средством улучшения погружения свай и свай-оболочек является
подмыв водой. Для этого применяют высоконапорные иглы и многоступенчатые
центробежные насосы типа ЦНС с расходом воды до 5 м
3
/мин и давлением до 33 МПа. В
сваях-оболочках малого диаметра подмывная труба вставляется внутрь («центральный
подмыв» — рис. 32). На время ее работы погружение сваи прекращают, включают
высоконапорную иглу, подмывную трубу опускают в прорези наголовника, так что она
выходит вниз из наконечника сваи. По окончании подмыва трубу втягивают обратно.
Таблица 16
Техническая характеристика вибромолотов для погружения и извлечения
шпунта
Показатели
МШ-2М В-11/44 В-402 СП-83 РЕ 26.02
HVB40/2
6
отечественного производства фирмы D?nkers
Статический момент
массы дебалансов, кН · м
0,091;
0,113
0,084 0,1;
0,11
0,11 0,1 0,07 0,054
Частота вращения деба-
лансов, об/мин
970 1475 1300 1000 1630 2600
Вынуждающая сила макс,
кН
94; 117 90-260 270 240 260 400
Мощность электродви-
гателя, кВт
2х30 2х22 55 2х17 100 -
Масса вибромашины, т 4,1 2,5 3,0 4,9 1,33 0,93

Рис. 31. Схема работы агрегата Tiewood по задавливанию стального шпунта (1—
8 — шпунтины):
а—г — схемы производства работ
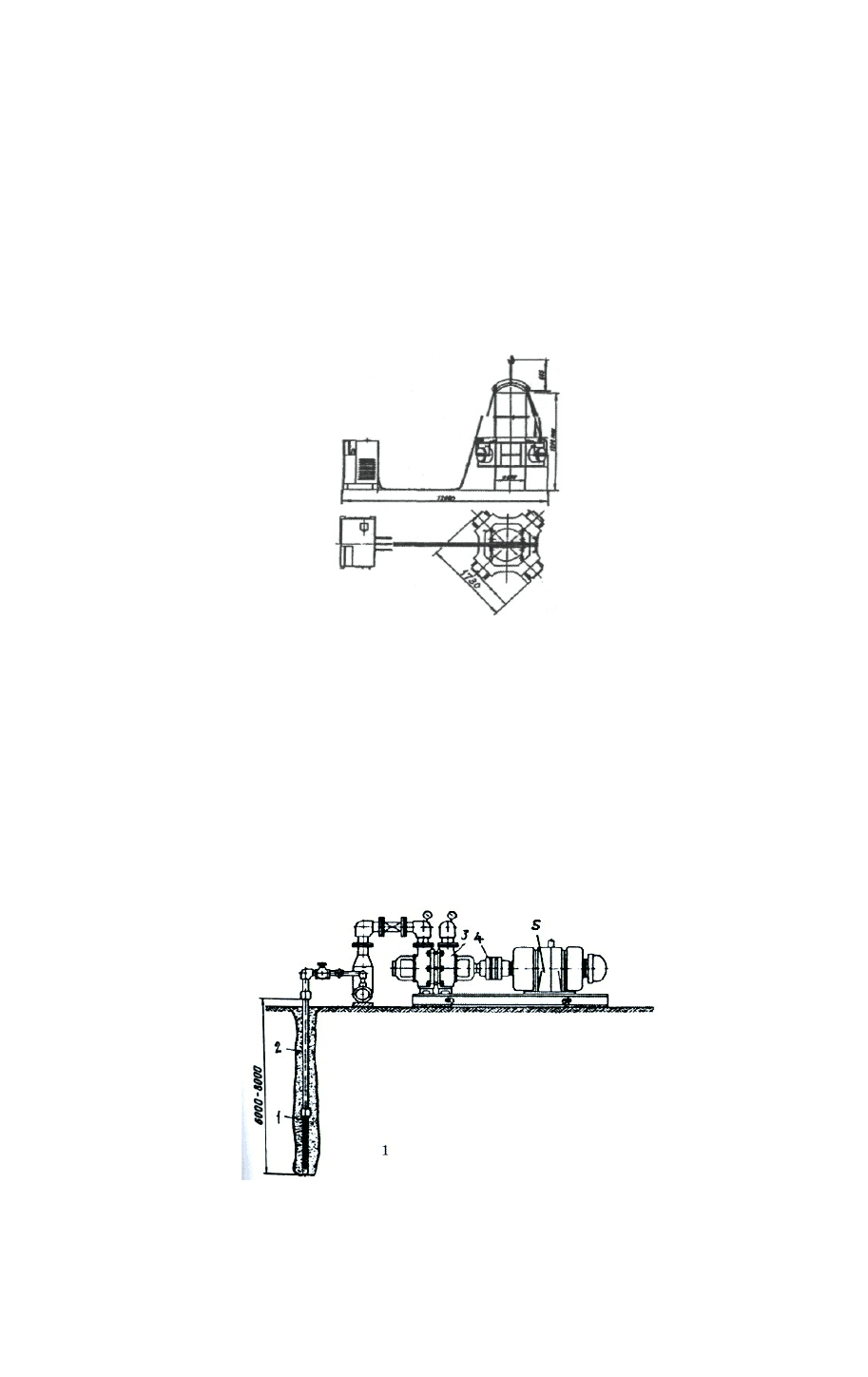
Рис. 32. Схема погружения сваи-оболочки с «центральным подмывом»:
1 - молот; 2 - наголовник; 3 - прорезь; 4 - подмывная труба; 5 - свая-оболочка; 6 -
центральное отверстие в наконечнике сваи; 7 — высоконапорная игла
Рис. 33. Схема погружения сваи-оболочки с наружным подмывом:
1 — нож; 2 — свая-оболочка; 3 — коллектор; 4 — резиновые шланги; 5 — пакет
подмывных труб
При подмыве оболочек большого диаметра используют пакет подмывных труб,
соединенный сверху коллектором (рис. 33). На время подмыва погружение оболочки
прекращают, включают подмывные иглы, пакет погружается в размываемый грунт. По
окончании подмыва пакет труб краном извлекают на поверхность. Работы по срезке
голов свай на сегодняшний день механизированы еще недостаточно. Для этих целей
может применяться навесное гидрооборудование («ножницы») на краны. Например,
гидрооборудование на рис. 34 предназначено для разрушения призматических свай
сечением до 45 х 45 см и свай-оболочек диаметром до 0,6 м. Усилие, развиваемое
гидроцилиндром, составляет 1100 кН, масса комплекта оборудования — 2,4 т.
Рис. 34. комплект гидрооборудования для разрушения голов свай
При небольшом объеме притока воды в котлован со шпунтовым ограждением
используют погружные центробежные моноблочные насосы типа ГНОМ
производительностью 10-40 м
3
/ч. При значительном притоке воды в котлован используют
центробежные самовсасывающие одноступенчатые насосы типа НЦС производитель-
ностью 18—130 м
3
/ч которыми можно откачивать и загрязненную воду.
Рис. 35. Иглофильтровая установка:
1 – иглофильтр; 2 – всасывающая труба; 3 – центробежный насос; 4 – муфта; 5 -
электродвигатель
При необходимости понижения уровня грунтовых вод в зоне котлована в несвязных
грунтах применяют иглофильтровые установки (см. рис. 35) .
5.5. Машины для фундаментов на вечномерзлых грунтах
При строительстве фундамента на вечномерзлых грунтах (ВМГ) их используют по
одному из двух основных принципов: по принципу I, предусматривающему сохранение
грунта в мерзлом состоянии весь период строительства и эксплуатации сооружения; по
принципу II, допускающему деградацию (частичное или полное размерзание) вечной
мерзлоты. Принятый принцип определяет выбор конструкции фундамента технологию и
механизацию его возведения.
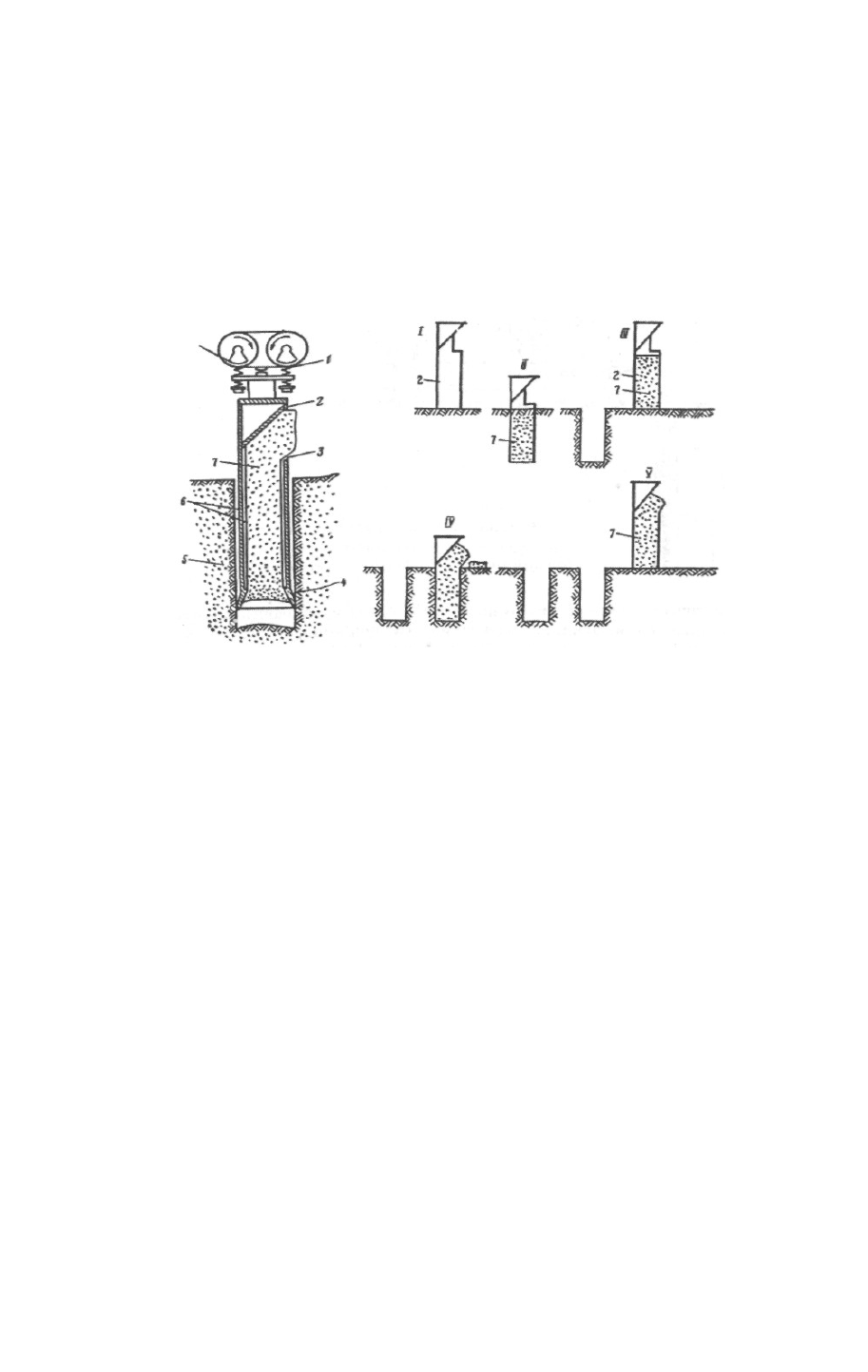
Рис. 36. Схема разработки скважин трубчатыми лидерами (I—V —
последовательность операций):
1 - вибромолот; 2 - лидер; 3 - отверстие для выхода грунта в лидерной скважине; 4 —
наконечник лидера; 5 — мерзлый грунт; 6 — зазоры между мерзлым грунтом и лидером;
7 — грунтовый керн
Из-за достаточно низких физико-механических характеристик ВМГ при
использовании обоих принципов, как правило, устраивают свайные фундаменты. В
случае применения принципа I сваи погружают забивкой в предварительно пробуренные
лидерные скважины меньшего диаметра или же устанавливают готовые свайные
элементы (буроопускные столбы) в скважины большего диаметра, заполняя полость
различными смесями (цементно-песчаным раствором, пескоцементом и др.).
Чтобы образовать лидерные скважины, используют обычную буровую технику для
скальных пород (см. п. 5.3), а также специальные трубчатые лидеры (рис. 36),
виброгрейферы, виброударные машины на базе тракторов, оборудованные
вибромолотами (рис. 37) [23].
При использовании принципа II в ряде случаев производят предварительное
оттаивание ВМГ с последующим сооружением свайного фундамента обычным способом.
Для оттаивания грунта применяют комплект оборудования, включающий источник пара,
паропровод, распределитель, паровые иглы (рис. 38, 39). В качестве источника пара

используют котлы с поверхностью нагрева от 8 до 32 м
2
. На одну иглу требуется
обеспечить 4-5 м
2
поверхности нагрева котла. Паровые иглы изготавливают из труб
диаметром 25-30 мм и длиной до 8 м.
Рис. 37. Виброударная машина для разработки скважин в мерзлых грунтах
Рис. 38. Паровая игла (а) и наконечники (б-г):
1 - заглушка; 2 - рукоятка; 3 - тройник; 4 - гибкий шланг; 5 - труба; 6 - наконечник; 7 -
вечномерзлый грунт; 8 - оттаянный грунт; 9 - сезонномерзлый грунт; 10 - лунка
Рис. 39. Перфорированная паровая игла:
1 — труба; 2 — отверстия; 3 — заглушка; 4 — рукоятка; 5 — гибкий шланг

6. ГРУЗОПОДЪЕМНЫЕ МАШИНЫ
Для отечественного мостостроения характерно создание и широкое применение
наряду с общестроительными кранами различных грузоподъемных кранов специального
назначения. Это объясняется особенностями технологии мостовых работ и
неблагоприятными условиями для применения в ряде случаев общестроительных кранов.
Основные типы и марки современных кранов рассмотрены в [10] —[14] и др. В данном
разделе приводятся дополнительные сведения о грузоподъемных машинах специального
назначения, которые обычно малодоступны студентам.
6.1. Типы грузоподъемных кранов
По области применения и эксплуатационным условиям краны для строительства
мостов можно разделить на три группы [24].
Первую группу составляют стреловые самоходные полноповоротные краны общего
назначения на спецшасси, автомобильном, пневмоколесном, гусеничном и
железнодорожном ходу. В отдельных случаях используют также башенные краны
(приставные, самоподъемные и передвижные). Краны этой группы применяют наиболее
широко. Их особенности — автономность работы, быстрота и низкая трудоемкость
приведения из транспортного в рабочее положение, но сравнительно высокая стоимость.
Во вторую группу входят специализированные универсальные краны: козловые и
жестконогие деррик-краны. Их отличительные особенности: более узкая область
применения, питание двигателей от внешних источников, меньшая стоимость, но и
повышенные трудозатраты, а также стоимость приведения в рабочее положение.
Третья группа - специальные краны, предназначенные для производства работ в
особых условиях. К ним относятся консольные, консольно-шлюзовые и кабельные краны,
специальные монтажные агрегаты.
Особую группу составляют плавучие краны — непременный атрибут строительства
любого большого моста. Сюда же можно отнести краны на самоподъемных платформах и
некоторые другие.
6.2. Стреловые самоходные краны общего назначения
Стреловые самоходные краны являются одним из наиболее универсальных средств
механизации строительно-монтажных работ. Многообразие существующих конструкций

и типоразмеров кранов дает возможность рационального выбора крана, наиболее соответ-
ствующего условиям его работы в конкретных условиях.
Основными факторами, определяющими грузоподъемные возможности стрелового
крана, являются устойчивость положения крана при действии опрокидывающего
грузового момента и высота подъема крюка крана относительно уровня его стоянки.
Влияние указанных факторов графически представляется в виде номограмм
грузовысотных характеристик, т. е. совмещенных графиков зависимостей G =f
1
(L) и H
=f
2
(L), где G - грузоподъемность крана, т; H -высота подъема крюка, м; L - вылет крюка,
м (рис. 40). Грузовысотные характеристики даны в справочниках для каждого крана при
работе его как без выносных опор (аутригеров), так и на них, для разных длин стрелы l
С
крана.
Кривые высоты подъема груза заданного габарита В рассчитаны по приведенной ниже
методике, пригодной для любого стрелового крана.
Высота подъема верхней кромки груза
,
)(2
)()(
)(
22
22
h
cL
lkfcLlB
cLlH
(23)
где l - расчетная длина стрелы крана; L - вылет крюка; с - расстояние от оси вращения
поворотной платформы крана до оси пяты стрелы; В - габарит груза; f- толщина стрелы в
месте предполагаемого соприкосновения с грузом; k-допустимый зазор между стрелой
крана и грузом; h — расстояние от опорной поверхности крана до оси пяты стрелы.
Рис. 40. Номограмма грузовысотных характеристик стрелового крана:
1— кривая грузоподъемности при работе крана без выносных опор; — то же, на
выносных опорах; 3 — кривая высоты подъема верхней кромки груза данного габарита; 4
— кривая высоты подъема крюка; 5 — дуга, описываемая концом стрелы

Расчетная длина стрелы крана складывается из следующих составляющих (см. рис.
40):
l = l
c
+ l
2
= l
1
+ l
2
+ l
3
cos α (24)
,
)(
)()(
22
2222222
2
ScL
cLlcLSSlSSl
l
ccc
(25)
где l
c
=
l
1
+ l
3
cos α — длина стрелы (расстояние между осью пяты и осью верхнего
блока грузового полиспаста основного подъема); S = l
3
sin α — расстояние от оси блока
полиспаста до продленной оси стрелы.
Определение высоты подъема груза по грузовысотным характеристикам производится
следующим образом:
1) зная массу груза G, находим соответствующую точку на кривой грузоподъемности
(см. рис. 40, график 2);
2) проводим вертикальную линию до пересечения с осью абсцисс и определяем
вылет стрелы L, соответствующий грузоподъемности;
3) продолжаем вертикаль до пересечения с кривой, соответствующей высоте
подъема крюка (см. рис. 40, график 4);
4) проводим горизонталь до пересечения с ординатой высоты подъема крюка и
определяем максимальную высоту подъема H, соответствующую вылету стрелы L.
Если задан габарит груза В, аналогично можно поступить с определением
максимальной высоты подъема верхней кромки груза (см. рис. 40, график 3). При этом в
задаче фигурируют толщина стрелы крана f и допустимый зазор между стрелой и грузом
k, которые в расчетах принимают приближенно по 1,0 м. Технолог-мостостроитель
занимается решением задачи о подборе грузоподъемного крана весьма часто. Причем
данная задача может решаться по крайней мере в двух постановках:
1. Для заданных технологических условий, т. е. H
3
, G
3
, В и параметрах
строповочных устройств, необходимо определить необходимые вылет L, длину стрелы l
с
и подобрать по справочнику марку крана.
2. Проверить возможности конкретного крана по установке груза с параметрами
G
3
и В на высоту H
3
.
В любом случае должны соблюдаться условия
G(L) ≥ G
3
; (26)
H(L) ≥ H
3
(27)
k ≥1м; (28)
L
min
≤ L ≤ L
max
; (29)

H ≤ H
mах
, (30)
где L
min
, L
max
— соответственно минимально и максимально допустимый вылет стрелы
по техническим характеристикам крана; H
mах
— максимально допустимая высота подъема
крюка.
Решение задачи типа 1 осложняется тем, что вокруг точки, отстоящей на расстоянии
k +f/2 от крайней точки груза (конструкции), может быть описано под разными углами к
горизонту бесчисленное множество стрел с параметрами L и l (l
с
). Причем уменьшение
вылета L, при котором увеличивается грузоподъемность G(L), приводит к возрастанию
длины стрелы l, а значит, к обратному эффекту — снижению грузоподъемности крана.
Как видим, эти два искомых параметра одновременно присутствуют в выражениях (23)—
(25), поэтому аналитически выразить один из них невозможно.
Во многих учебниках и справочниках приводятся формулы для определения
расчетных параметров подбираемого крана. Но в силу изложенных выше особенностей,
практический расчет по формулам вызывает затруднения и приводит к неверным
результатам. Поэтому более просто и реально решается задача 2, причем лучше всего ее
решать графическим построением схемы монтажа в масштабе.
При решении этой задачи известны: масса груза со строповочными приспособлениями
G = G
3
, габарит груза В и требуемая высота его подъема H = H
3
(см. рис. 40). Берем
конкретный кран и принимаем для начала длину его стрелы приближенно (1,3...1,5) H
3
.
Выбираем по справочнику ближайшую (в большую сторону) длину стрелы l (l
с
).
Далее производим графические построения: из точки, отстоящей на расстоянии k +f/2
от крайней точки груза (конструкции), проводим наклонную прямую, добиваясь того,
чтобы между точкой ее пересечения с уровнем расположения шарнира пяты стрелы h и
точкой пересечения с осью подвешивания груза длина отрезка была равна длине стрелы.
При этом стремимся достичь минимума вылета стрелы L. Если стрела не укладывается
между указанными точками, то либо k > 1 м, что вполне приемлемо, либо можно
уменьшить длину стрелы. Если же наоборот — стрела «режет» груз, необходимо
увеличить ее длину.
При полученном таким образом вылете стрелы L по грузовысотным характеристикам
крана проверяем условия (26)—(30). При несоблюдении хотя бы одного из них кран «не
проходит», необходимо выбрать из числа имеющихся кранов приемлемый, повторив
заново всю описанную схему решения задачи.
Пример 4. Проверим возможность установки балки пролетного строения массой G
3
=
12 т на опоры путепровода пневмоколесным краном КС-6362 грузоподъемностью 40 т.
Исходные данные (рис. 41): h
0
= 7 м; h
3
= 1 м; h
K
= 2 м; h
c
= 3 м; В = 4 м; h = 1,5 м; с =

2,5 м; d ≥ 0,5 + 1 = 1,5 м.
Решение: определяем заданную высоту подъема крюка
H
3
= h
0
+ h
3
+ h
K
+ h
c
= 7 + 1 + 2 + 3 = 13 м.
Рис. 41. Схема монтажа конструкции (к примеру 4)
Необходимая длина стрелы l
с
1,5 · 13 = 19,5 м. По справочнику [24] принимаем
кран с длиной стрелы 20 м (с. 57, рис. 3.26).
Путем графического построения при выполнении условия (28) получен минимально
возможный вылет стрелы L = 9 м.
Условие (29) соблюдается: L
min
= 5,5 м ≤ L≤ L
max
= 17 м.
По грузовысотным характеристикам (рис. 3.27, кривая 11) G(L) = 13 т, т. е. условие
(26) соблюдено. По кривой 10 — H(L) = 19 м > H
3
= 13 м, т. е. выполняются и условия
(27), (30).
Таким образом, пневмоколесный кран КС-6362 с длиной стрелы 20 м может
выполнить требуемую монтажную операцию.
В России и странах ближнего зарубежья серийно выпускаются автомобильные краны
грузоподъемностью 4—16 т, пневмоколесные — 16-100 т, гусеничные — 16—150 т, на
спецшасси автомобильного типа — 25—160 т. Имеются опытные образцы кранов на
спецшасси грузоподъемностью до 250 т. Довольно широко применяются также краны
японских фирм на специальном шасси нормальной базы фирмы Kato грузоподъемностью
16—120 т, гусеничные краны фирм Hittachi и Sumitomo, германские краны Liebherr,
финские Lokomo — грузоподъемностью до 250 т. Известны случаи осуществления
уникальных монтажных операций кранами на спецшасси грузоподъемностью до 650 т.
При монтаже пролетных строений железнодорожных мостов и строительстве
