Волков В.Л. Моделирование процессов и систем
Подождите немного. Документ загружается.

20
F e I Adt A
dt
A
dt
T dtI Adt A
dt
A
dt
D
G dtI Adt A
dt
A
dt
B
Adt
= = + + + +
= + + + +
= + + + +
2
2
3
3
2 2
3
3
4
2 2
3
3
4
2 3
2 3
2 3
!
...,
(
!
...),
(
!
...),
(3.3)
где I - единичная матрица; dt - период дискретизации системы (процесса).
Период дискретизации dt выбирается исходя из полосы пропускания ДС в
соответствии с импульсной теоремой (полоса пропускания определяется по
амплитудно-частотной характеристике).
Детерминированной является ДС, у которой отсутствуют шумы
возмущения и нет стохастических процессов (или всеми этими факторами
можно пренебречь). У стохастической ДС отсутствует детерминированный
вектор входных сигналов.
Объектами наблюдения в ДС, заданными уравнениями (3.1) или (3.2),
являются информационные процессы, объекты управления, датчики
первичной информации (ДПИ), исполнительные устройства. Объект
наблюдения может быть также задан передаточными функциями,
связывающими входы и выходы. Модель объекта наблюдения или в более
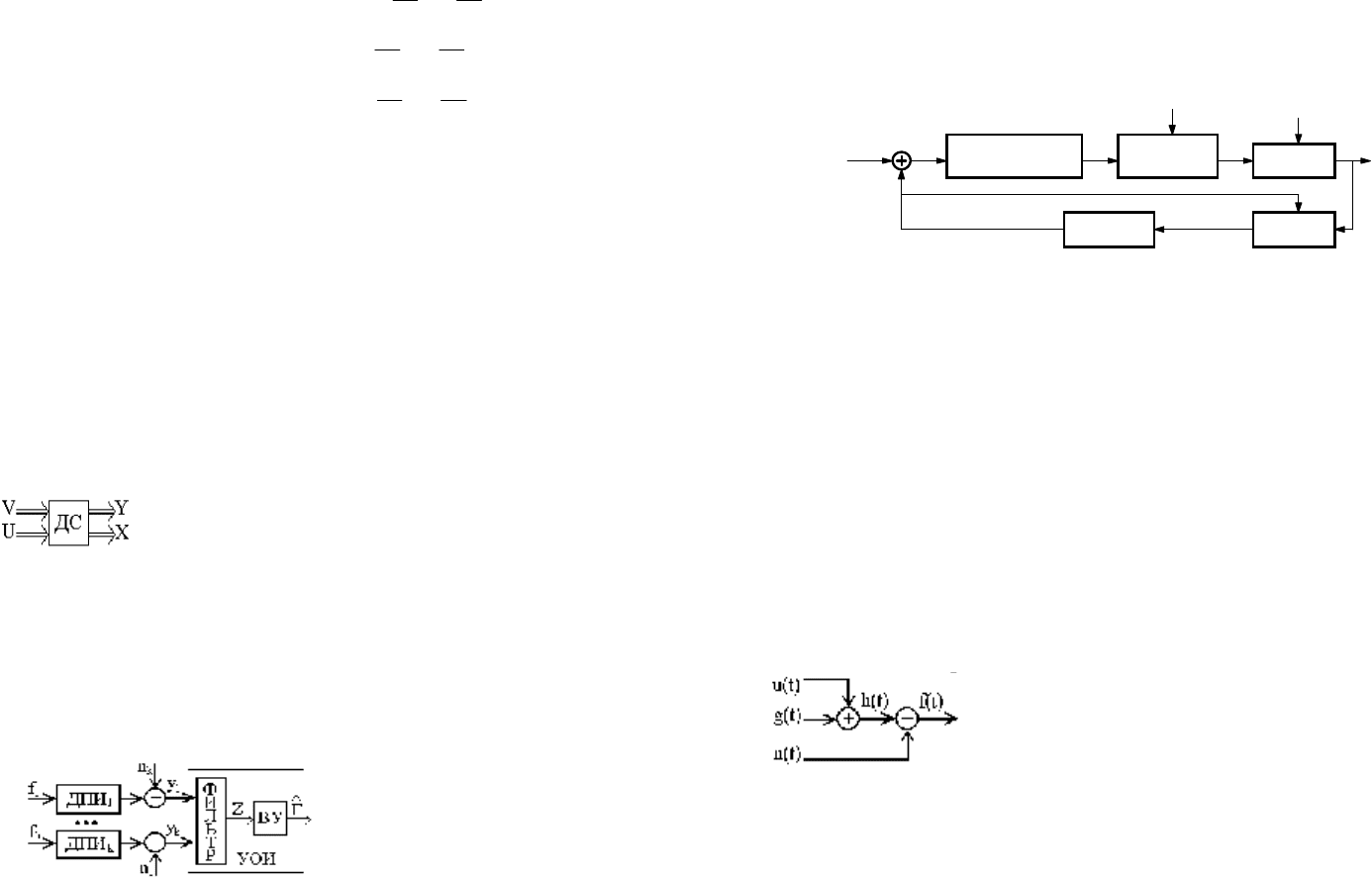
общем случае ДС определяется структурной схемой,
приведенной на рис.3.1, где X - вектор состояния системы;
U - вектор входа; V - вектор возмущения (или
формирующих белых шумов для стохастических сигналов);
Y - вектор выхода. Связь векторов U, V, Y, X определяется соотношениями
(3.1), (3.2).
Информационно-измерительная система имеет ДПИ, измеряющие
физические величины; устройство обработки информации УОИ с фильтрами
и вычислительными устройствами ВУ (рис.3.2). На основе измерений f
1
,...,f
k
,
полученных
с аддитивными
шумами n
1
,...,n
k
,
ИИС определяет
оптимальные оценки
F^=(f^
1
,...,f^
k
).
Датчик первичной
информации - элемент
устройства, преобразую-щий
информацию о физической
величине в сигнал, удобный для исполь-зования и обработки. Он задается
Рис3.1
Рис.3.2
21
дифференциальным уравнением или передаточной функцией. Передаточной
функцией ДПИ является отношение преобразования Лапласа выходного
процесса ДПИ к преобразованию Лапласа входного процесса при нулевых
начальных условиях.
Система автоматического управления - это комплекс устройств,
Исполнительное
устройство
Объект
управления
Датчики
Регулятор Фильтр
Uoc=-LX(k/k) X(k/k)
U
з
V(k)
N(k)
Y(k)X(k)
Рис.3.3
предназначенный для автоматического изменения одной или нескольких
регулируемых величин объекта управления с целью поддержания желаемого
режима работы (цели управления). Целью управления может быть:
стабилизация регулируемых величин, программное и следящее управление
регулируемых величин, оптимизация регулируемых величин. В САУ (рис.3.3)
исполнительное устройство и объект управления составляют объект
наблюдения и представляют динамику системы.
3.1.1. Модели информационных процессов
Основные процессы систем: U(t) - детерминированный векторный
полезный процесс; G(t) - случайный векторный полезный процесс; N(t) -
шумы измерений; X(t) - компоненты вектора состояния системы; Y(t) -
выходные сигналы системы. Для одномерного случая взаимодействие
сигналов и шумов показано на рис.3.4. Случайная
составляющая g(t) информационного процесса
задана спектральной плотностью Sg(w).
Детерминированная составляющая задана сигналом
u(t); h(t)=g(t)+u(t) - полный информационный
процесс; f(t)=h(t)+n(t) - измерение процесса h(t) с
аддитивными шумами n(t) безынерционным ДПИ.
Параметры детерминированного сигнала задаются
в соответствии с описанием неслучайной составляющей входного сигнала.
Исходной моделью стохастического процесса является cпектральная
плотность, но для практического использования в алгоритмах обработки
информации, а также для численного и графического исследования при
Рис.3.4
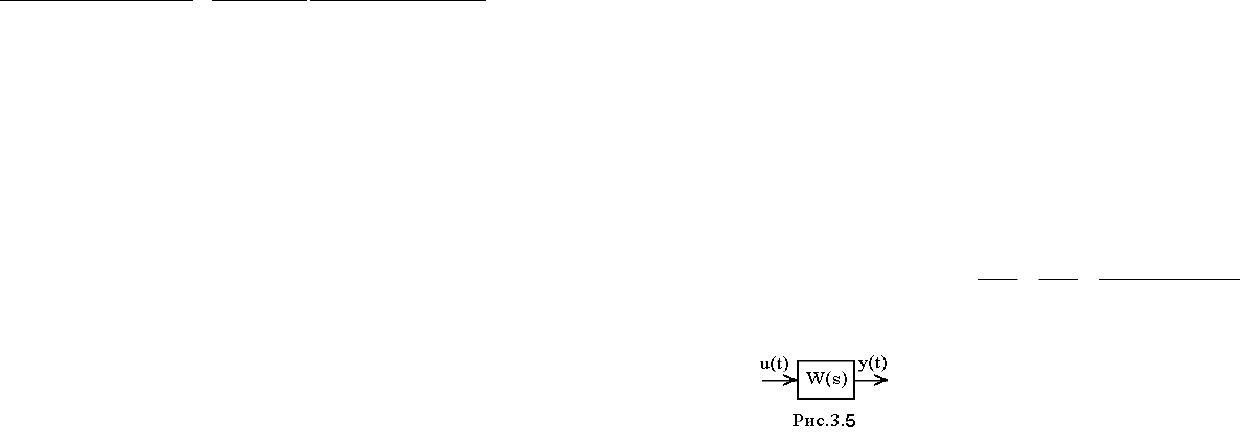
22
моделировании используют вторичные модели в виде передаточной функции
формирующего фильтра и матричных линейных уравнений [2].
Передаточная функция Wg(s) формирующего фильтра определяется при
факторизации исходной спектральной плотности Sg(s)=Wg(s)Wg(-s)Q, где Q -
интенсивность шума на входе формирующего фильтра; Wg(s),Wg(-s) -
дробно-рациональные функции, нули и полюсы которых лежат
соответственно в левой и правой комплексных полуплоскостях [2]. Учитывая
дробно-рациональность спектральной плотности, функцию Sg(w) записывают
Sg(w)=C(s/j)/D(s/j)=B(s)/A(s) B(-s)/A(-s). Из этого соотношения имеем
c cs c s
d ds d s
b bs
a as
b bs b s
a as a s
Q
m
m m
n
n n
m
m
n
n
m
mm
n
nn
0 1
2 2
0 1
2 2
0
0
0 1
0 1
1
1
1
1
− + + −
− + + −
=
+ +
+ +
− + + −
− + + −
... ( )
... ( )
...
...
... ( )
... ( )
.
(3.4)
При факторизации спектральной плотности используется следующий
алгоритм. Поскольку выражение Sg(s/j) представляется в виде (3.4), где
Q=Cm/Dn - интенсивность входного белого шума фильтра, задача
факторизации решается составлением аналитических выражений B(s)B(-s),
A(s)A(-s) и систем уравнений относительно Bj и Aj путем сравнения коэф-
фициентов выражений C(s/j) и B(s)B(-s), а также D(s/j) и A(s)A(-s). При n=1
a[0]=(d[0])
1/2
, a[1]=1. При n=2 a[0]=(d[0])
1/2
, a[1]=(2a[0]-d[1])
1/2
, a[2]=1. При
n>2 система уравнений решается итерационным методом. При n=3
a[2]=(d[2]+2a[1])
1/2
, a[1]=(2a[0]a[2]-d[1])
1/2
. При n=4 a[3]=(2d[2]-d[3])
1/2
,
a[1]=(2d[0]a[2]-d[1])
1/2
, a[2]=(d[2]-2a[0]+2a[1]a[3])
1/2
. Для коэффициентов Bj
составляются и решаются аналогичные уравнения при m=1,2,...,4. Для
представления модели формирующего фильтра в пространстве состояний
переходят от передаточной функции к дифференциальному уравнению g(t)
при входном формирующем белом шуме V(t):
a
n
g
(n)
(t)+...+a
0
g(t)=b
m
V
(m)
(t)+...+b
0
V(t).
Пример. Измерение аэродинамических характеристик вращающихся
лопастей вертолета в условиях полета. Измеряется перепад давлений между
верхней и нижней поверхностями лопасти вертолета в n точках, при этом
осуществляется суммирование сигналов датчиков, установленных в каждом
сечении (m датчиков), опрашивается m/n каналов с определенной частотой и
регистрируются результаты. Элементом, воспринимающим информацию, в
данной схеме является дифференциальный индуктивный датчик. На датчик
действует неслучайный полезный сигнал u(t)=U
11
+A
1
sin(w
1
t), где U
11
-
постоянная составляющая полезного сигнала, определяемая подъемной силой
лопасти; A
1
sin(w
1
t) - переменная составляющая, возникающая за счет того,
23
что лопасть в процессе вращения поочередно движется то навстречу
набегающему потоку, то по нему; U
11
=13,5 Н/см
2
; A
1
=0,784 Н/см
2
; W
1
=240 с
-
1
, и случайная помеха n(t), которая образуется при наличии флюгерного
винта, большая скорость вращения которого образует местные искажения
потока. Помеха n(t) задана спектральной плотностью
Sn(w)=7000/(w
2
+12220000). Соответствующая передаточная функция
формирующего фильтра, найденная путем факторизации спектральной
плотности, имеет вид W(s)=84/(s+3500).
3.2. Методы формирования матричных моделей
Для составления алгоритмов обработки информации, а также для
численного и графического исследования движения ДС модель типа
передаточной функции преобразуют в матричную модель в пространстве
состояний (3.1) или (3.2). Модели ДС и процессов в виде матричных
уравнений на основе передаточной функции могут быть получены методами
[5,6,12] вспомогательной переменной, нормальной формы Коши,
интегрированием дифференциального уравнения, разложением передаточной
функции на сумму или произведение простых дробей. Для всех методов
рассматриваем передаточную функцию ДС
Ws
Ys
Us
Bs
Ds
b bs bs
d ds ds
m
m
n
n
()
()
()
()
()
...
...
,= = =
+ + +
+ + +
0 1
0 1
(3.5)
которая связывает вход и выход ДС линейным
преобразованием (рис.3.5) Соответствующее
дифференциальное уравнение определяется на
основе свойств преобразования Лапласа.
d
n
y
(n)
(t)+...+d
0
y(t)=b
m
u
(m)
(t)+...+b
0
u(t).
3.2.1. Метод вспомогательной переменной
Модель в пространстве состояний методом вспомогательной переменной
формируем на основе передаточной функции (3.5). Выразим y(s) из заданной
передаточной функции y(s)=B(s)/D(s) и введем замену переменной
R(s)=u(s)/D(s), откуда получим дифференциальное уравнение относительно
R(t) без производных в правой части d
n
R
(n)
+...+d
0
R=u(t). При этом выражение
для y(t) также не содержит производных в правой части: b
m
R
(m)
+...+b
0
R=y(t).
Матричная модель методом вспомогательной переменной для
стохастической составляющей представляется уравнением состояния и
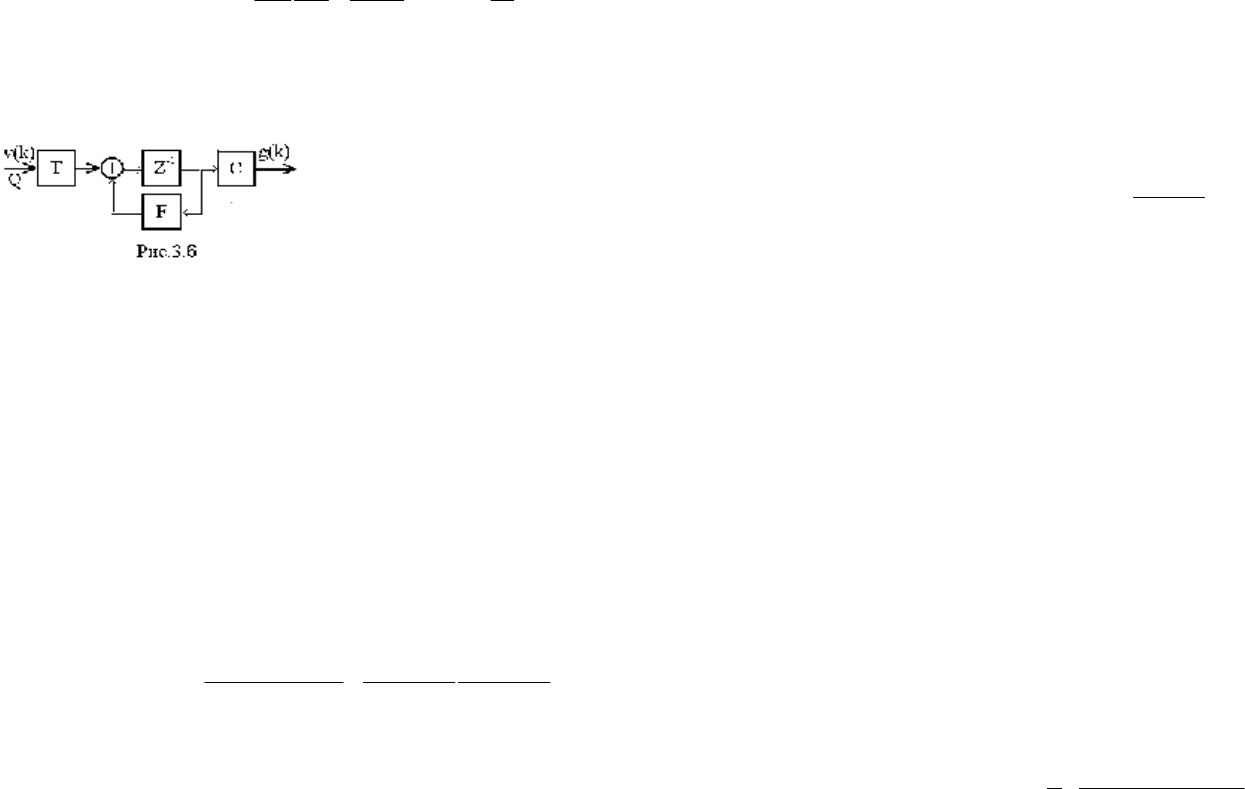
24
уравнением выхода: X′=AX+Du, y(t)=CX, где матрицы A, D, C
cоответственно равны:
A
d
d
d
d
d
d
D
d
n n
n
n n
=
− − −
=
−
0 1 0 0
1
0 1 1
...
...
...
, ...,
(3.6)
[
]
C b b
m
=
0
0 0... , ..
.
Дискретная модель (уравнение состояния и уравнение выхода)
Х(k+1)=FХ(k)+GU(k), y(k)=CX(k).
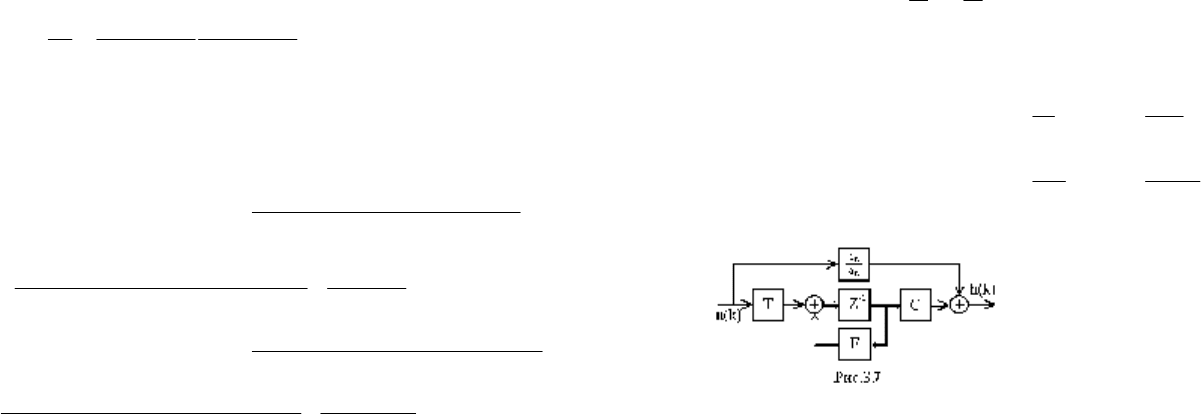
Схема дискретной матричной модели для
метода вспомогательной переменной
(рис.3.6) имеет входной сигнал u(k) и
выходной y(k), квантованные по времени с
периодом дискретизации dt.
Алгоритм формирования модели.
1. Определить передаточную функцию формирующего фильтра случайного
процесса на основе заданной спектральной плотности.
2. Определить частоту спектра информационного процесса (ИП) и
вычислить период дискретизации.
3. Составить непрерывные матричные модели ИП и выхода методом
вспомогательной переменной.
4. Сформировать дискретную матричную модель векторной случайной
последовательности при найденном периоде дискретизации.
5. Вычислить дисперсию и среднеквадратическое отклонение ИП.
Пример. Формирование модели стохастического процесса. Исходные
данные: Sg(w)=(w
2
+0,25)/(w
4
+1,98w
2
+1,0201).
Результаты: 1. Передаточная функция фильтра ИП определяется при
факторизации спектральной плотности Sg(s)=Wg(s)Wg(-s), где s=jw.
Sgs
s
s s
b bs
a as s
b bs
a as s
()
,
, ,
.=
−
− +
=
+
+ +
−
− +
025
198 10201
2
4 2
0 1
0 1
2
0 1
0 1
2
Находим коэффициенты bj, aj из систем нелинейных алгебраических
уравнений, получаемых при сравнении полиномов левой и правой части:
b bs s a a a s s s s
0
2
1
22 2
0
2
0
1
2 2 4 4 2
025 2 198 10201− =− + + − + = − +, , ( ) , , .
25
Системы уравнений имеют вид
b
b
a
a a
0
2
1
2
0
2
0 1
2
025
1
10201
2 198
=
=
=
− =−
, ,
,
, ,
, .
Получим: bo=0,5, b
1
=1, a
0
=1,01, a
1
=2, соответствующая передаточная
функция формирующего фильтра ИП Wg(s)=(s+0,5)/(s
2
+2s+1,01).
2. Максимальная частота спектра ИП определяется по полосе
пропускания формирующего фильтра ИП. В свою очередь, полоса
пропускания вычисляется как частота среза эквивалентной передаточной
функции разомкнутой системы (фильтра). Представим передаточную
функцию формирующего фильтра в виде
W(s)=0,495(2,02s+1)/(0,99s
2
+1,98s+1)=KWз(s). Определим передаточную
функцию разомкнутой системы по формуле
Wps
Wзs
Wзs
()
()
()
,=
−1
(3.7)
откуда Wp(s)=(2,02s+1)/(0,99s
2
-0,04s). Частота среза полученной
передаточной функции определяется в точке пересечения амплитудно-
частотной характеристики горизонтальной оси, т.е. при |Wр(jw)|
2
=1. Получим
выражение |Wр(jw)|
2
=(4,08w
2
+1)/(0,98w
4
+0,0016w
2
)=1, которое преобра-зуем
к виду 0,98w
4
-4,0784w
2
-1=0. Из полученного биквадратного уравне-ния
найдем частоту среза: Wc=4,4 рад/с. В соответствии с импульсной теоремой
период дискретизации ИП определяется dt=1/(2F
m
), где F
m
=Wc/2. Получим
dt=0,715 c.
3. Формирование модели ИП в матричной непрерывной форме
предполагает вычисление матриц уравнений состояния и выхода для
формирующего фильтра в соответствии с (3.6):
A B D=
−
=
=
0 1
-2
101
0
1
0
1,
, , ,
C=[1 0,5].
4. Дискретную модель ИП Х(k+1)=FХ(k)+GU(k)+TV(k), g(k)=CX(k)
рассчитываем на основании непрерывной по формулам (3.3).
F G T=
−
=
=
1 0,72
-0,44
073
0
072
0
072,
,
,
,
,
,
C=[1 0,5].
5. Дисперсия процесса определяется в соответствии со свойствами
спектральной плотности (2.5).
Dg
w
w w
dw=
+
+ +
∞
∫
1 025
198 10201
2
4 2
0
π
,
, ,
.
26
Используя факторизованное выражение спектральной плотности, получим
[ ]
Dg
j
s
s s
s
s s
ds s Sgs
k
k
n
j
=
+
+ +
−
− +
=
=
∞
∑
∫
1 05
101 2
05
101 2
2 2
1
0
π
,
,
,
,
Re ().
Интеграл вычислим через вычеты по левой комплексной полуплоскости.
Полюсы найдем из уравнения 1,01+2s+s
2
=0: s
1
=-1+0,1j, s
2
=-1-0,1j. Вычеты в
полюсах:
[
]
[
]
Res
k
s sk
k
Sgs s s Sgs() lim( ) ()= −
→
,
[ ]
Res
1
101
2
2
1 01
025
1 01 1 01 101 2
Sgs s j
s
s js j s s
s j
() lim ( , )
,
( , )( , )(, )
,
= +−
−
+− ++ − +
=
→−+
=
−
−
−
− −+ + − −
=
−
+
= +
025 1 02 001
02101 2 1 01 1 02 001
02 074
008 08
0155 0944
, ( , , )
, (, ( , ) ( , , ))
, ,
, ,
, ,
j
j j j
j
j
j
,
[ ]
Re () lim ( ,)
,
( ,)( , )(, )
,
sSgs s j
s
s js j s s
s j
2
101
2
2
1 01
025
1 01 1 01 101 2
= ++
−
++ +− − +
=
→−−
=
−
−
−
− −− + − −
=
−
−
−
= −
025 1 02 001
02101 2 1 01 1 02 001
02 074
008 08
0155 0944
, ( , , )
, (, ( ,)( , ,))
, ,
, ,
, ,
j
j j j
j
j
j
.
Получим дисперсию Dg=0,155+0,944j+0,155-0,944j=0,31 и по формуле (2.3)
среднеквадратическое отклонение σ
g
=0,557.
Выводы: Матричная модель случайного ИП является универсальной,
легко реализуемой при моделировании на ЦВМ. Недостатком метода
является необходимость того, что порядок числителя исходной спектральной
плотности ИП должен быть меньше порядка знаменателя.
3.2.2. Метод последовательного интегрирования
При формировании матричной модели ДС методом последовательного
интегрирования в соответствующем дифференциальном уравнении системы
n-го порядка перенесем в правую часть слагаемые левой части и объединим
их со слагаемыми, имеющими одинаковый порядок производной [7]: [a
n
y
(n)
(t)-
b
n
u
(n)
(t)]+...+[a
0
y(t)-b
0
u(t)]=0. Интегрируем полученное выражение [a
n
y(t)-
b
n
u(t)]
(n-1)
+...+[a
1
y(t)-b
1
u(t)]
(1)
+x
1
=0, где переменная x
1
определяется
соотношением x
1
'=a
0
y(t)-b
0
u(t). Интегрируем уравнение, содержащее
переменную x
1
:
[a
n
y(t)-b
n
u(t)]
(n-2)
+...+[a
2
y(t)-b
2
u(t)]
(1)
+x
2
=0, где переменная x
2
определяется соотношением x
2
'=a
1
y(t)-b
1
u(t)+x
1
. Повторим процесс
интегрирования еще n-2 раза, вводя вспомогательные пере-менные x
3
,...,x
n
.
Последнее уравнение системы примет вид a
n
y(t)-b
n
u(t)+
27
+x
n
=0, откуда
yt
a
x
b
a
ut
n
n
n
n
() ()=− +
1
. Из системы уравнений для x
j
получим
матричное уравнение состояния X’=AX+Du, где матрицы А, В соответственно
равны:
A
a
a
a
a
B
ba
a
b
ba
a
b
n
n
n
n
n
nn
n
n
=
=
−
−
−
−
0 0...0 -
0 0...0 -
0
-1
..... , ......
0
0
1
1
. (3.8)
Запишем уравнение выхода в
соответствии с полученным уравнением
y(t) в матричном виде y=CX, получим
C=[0,...,0,-1/a
n
]. Схема формирования
выходного сигнала ДС представлена на
рис.3.7.
Пример. Задана передаточная
функция ДС W(s)=(2s+12)/(3s
2
+24s+21). Для данного примера получим
непрерывную матричную модель X’=AX+BU по (3.8) и матрицу C уравнения
выхода:
A B=
=
−
0 -7
1 -8
-2
, ,
12
C=[0 0,33].
3.2.3. Метод нормальной матричной формы Коши
Формирование матричной модели ДС методом нормальной формы Коши
заключается в следующем. В дифференциальном уравнении n-го поряд-ка
обозначаем компоненты вектора состояния [6]: y
(j)
=x
j+1
для j=0,...,n-m-1,
y x C u
j
j jk
k
k
j nm
() ()
( )
= +
+ −
=
−
−
∑
1
0
для j=n-m,...,n-1.
Уравнения для переменных состояния x
1
,...,x
n
приобретают вид
x
j
'=x
j+1
(j=1,...,n-m-1), x
j
'=x
j+1
+C
j
U (j=n-m,...,n-1).
Найдем x
n
', полагая j=n-1,
y x C u x y C u
n
n n k
k
n
n
nk
k
k
m
k
n nm
( ) () () () ()
( )
, .
−
−− −
==
−
−
−
= + = −
∑∑
1
1
1
10
1
Из последнего уравнения выразим y
(n)
:
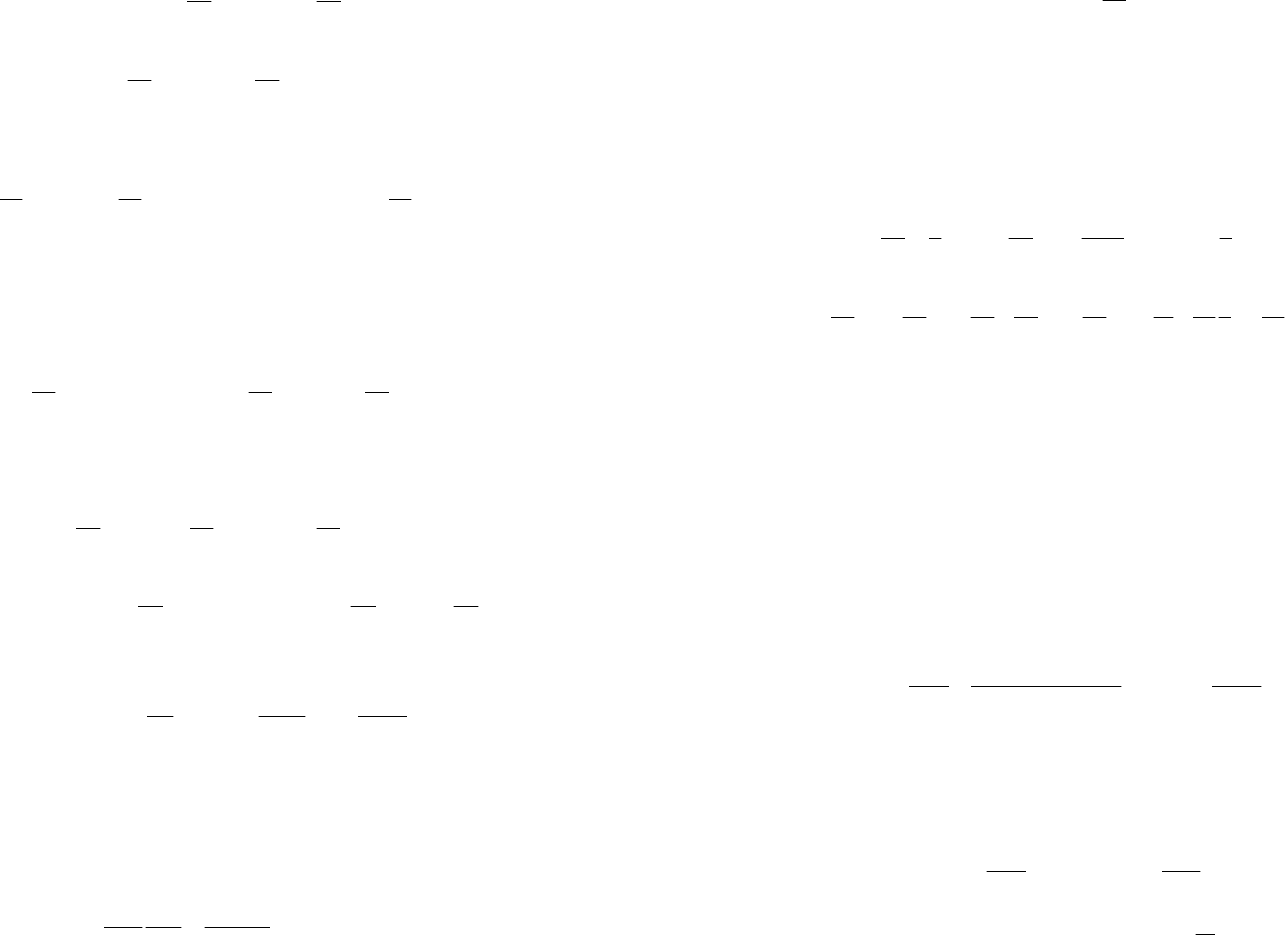
28
y
a
ay
a
bu
n
n
j
j
n
k
k
k
m
j
n
() () ()
,=− +
==
−
∑∑
1 1
01
1
x
a
ay
a
bu C u
n
n
j
j
n
k
k
k
m
j
n
nk
k
k
m
() () () ()
.
1
01
1
1
1 1
=− +
==
−
−
=
∑∑ ∑
-
Подставим y
(j)
, получим первую производную n-й компоненты X:
x
a
ax
a
a C u
a
bu C u
n
n
jj
j
n
n
j
jnm
n
jk
k
k
j nm
n
k
k
nk
k
k
m
() ()
( )
() ()
.
1
1
1
1 1
0 0
1 1 1
=− − + −
+
=
−
=−
−
−
=
− −
−
=
∑ ∑ ∑ ∑
Учтем равенство
a C u u aC
j jk
k k
k
m
k
j nm
jnm
n
j jk
jnmk
n
−
=
−
=
− −
=−
−
−
=−+
−
= =
∑∑∑ ∑
() ()
( )
0
1
0
1 1
и
получим
x
a
a
x u
a
a
C
b
a
u C u
n
j
n
j
j
n
k
k
m
j
n
jk
k
n
k
nk
k
k
m
k
m
jnmk
n
() () () ()
.
1
1
0
1
0
1
10
1
=− − + −
+
=
−
=
−
− −
===−+
−
∑ ∑ ∑∑∑
Полагая коэффициенты при производных входного сигнала равными нулю,
получим
C
b
a
C
b
a
a
a
C k m
nm
m
n
nk
k
n
j
n
jk
jnmk
n
− − −
=−+
−
= = −
= −
∑
, ( ... ), 1 1
1
x
a
a
x Cut C
b
a
a
a
C
n
j
n
j n n
j
n
n
j
n
j
jnm
n
()
(),
1
1
0
1
0
1
=− + = −
+
=
−
=−
−
∑ ∑
или в общем виде
C
b
a
C
b
a
a
a
C
n
n
j
n j
n
n j
n
k
k
j
0
0
1
= = −
− −
=
−
∑
,
. (3.9)
Матрицы A, B, C для нормальной канонической формы Коши (X′=AX+BU,
y=CX) имеют вид
[ ]
A
a
a
a
a
a
a
B C
C
C
ng ng
ng
ng
nm
n
=
− −
−
=
−
−
0 1 0
0
0 1
1
=1,0,...,0
...
...
...
,
....
....
, .
(3.10)
29
Выходной сигнал ДС в общем случае
yt
b
a
x ut
n
n
() ().= +
1
Пример. Передаточная функция датчика W(s)=(3s
2
+12s+15)/(2s
4
+
+20s
3
+50s
2
+60s+28). Найдем матрицы A, D, C в соответствии с (3.10).
Выходной сигнал ДС в общем случае y(t)=X
1
b
n
/a
n
+u(t). Найдем
коэффициенты матриц, учитывая данные передаточной функции (m=2, n=4,
b
2
=3, b
1
=12, b
0
=15, a
4
=2, a
3
=20, a
2
=50, a
1
=60, a
0
=28). Коэффициенты Сj
(j=n-m,...,n) в этом случае равны (3.9):
C
b
a
C
b
a
a
a
C
j
j
о2
2
4
3
1
4
1
4
0
2
3
2
610
3
2
9= = = − = − =−
+
=
∑
, ,
C
b
a
a
a
C
b
a
a
a
C
a
a
C
j
j
j4
0
4 4
0
3
0
4
2
4
2
3
4
3
15
2
50
2
3
2
9
20
2
60= − = − − = − + =
=
∑
.
Матрицы А, В, С соответственно равны:
[ ]
A B C=
− − −
=
−
=
1 0 0
0 1 0
0 0 1
-10
0 0 0
0
0
0
14 38 25
0
15
9
60
1,
,
, .
Уравнение выхода y(t)=X
1
(t).
3.2.4. Метод представления передаточной функции суммой дробей
Для получения матричной модели ДС методом разложения передаточной
функции на сумму простых дробей ее полюсы должны быть
действительными. Передаточная функция представляется [7]
Ws
Bs
As
b bs bs
a as as
C
C
s s
m
m
n
n
j
j
j
n
()
()
()
...
...
,= =
+ + +
+ + +
= +
−
=
∑
0 1
0 1
0
1
где C
j
- коэффициенты, которые могут быть найдены при сравнении
числителей передаточной функции левой и правой частей или при
использовании вычетов. При простых полюсах передаточной функции
коэффициенты
C
Bs
As
s s
Bs
As
j
s sj
j
=
= −
→
Res
()
()
lim( )
()
()
.
Коэффициент C
0
находится из условия
C Ws
b
a
s
n
n
0
= =
→∞
lim ()
.
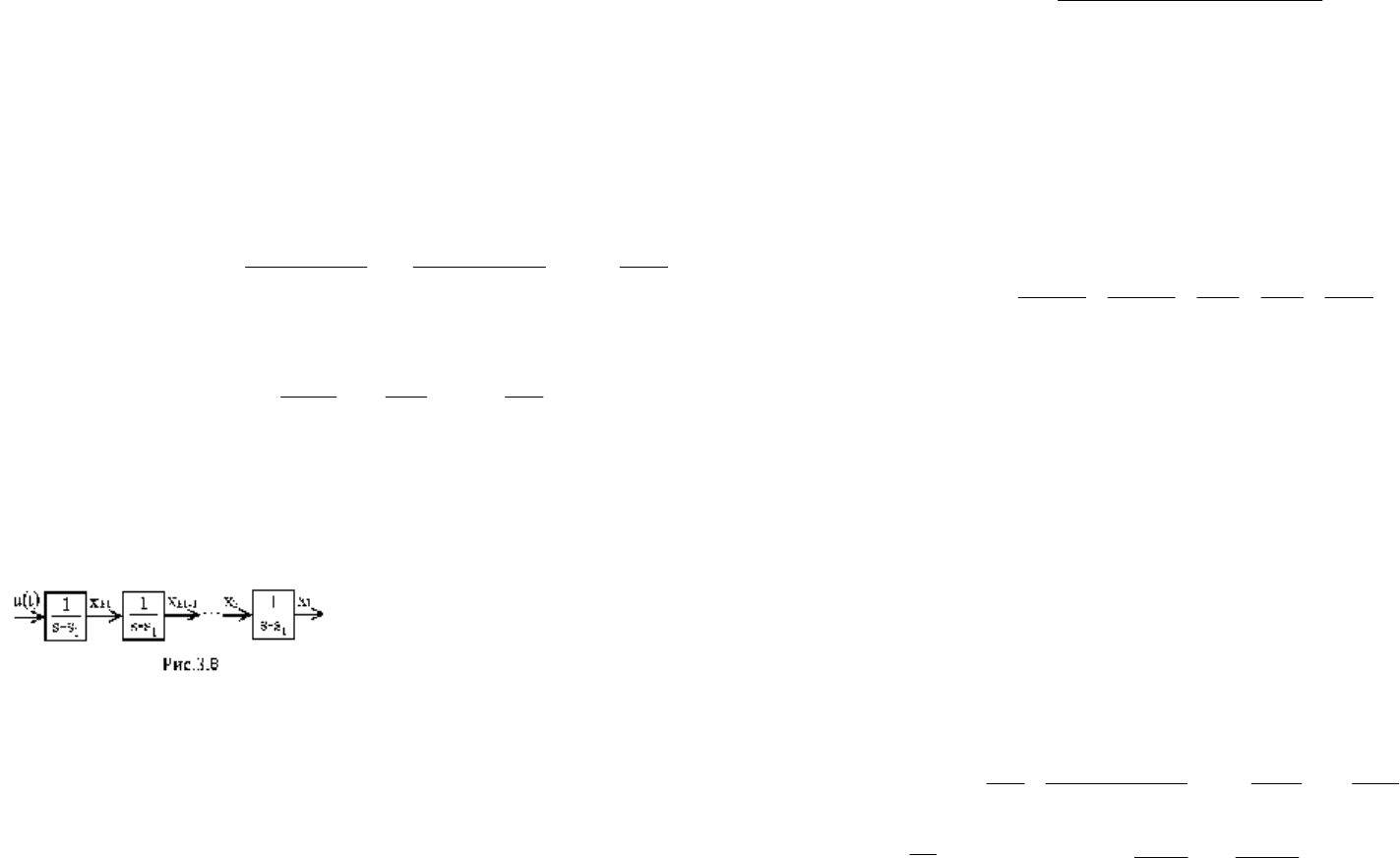
30
Обозначим компонентами вектора состояния
X s us s s
j j
() ()/( )= −
и
получим матрицы уравнения состояния
A
s
s
s
B
n
=
=
0 0
0 ...0
...
0
2
1
1
1
1
,
...
.
Из уравнения выхода
yt Cut CX
j j
j
n
() ()= +
=
∑
0
1
матрица C=[C
1
,...,C
n
].
При наличии кратных полюсов передаточной функции матрица А
приобретает форму Жордана. Отличие от предыдущего случая заключается в
представлении передаточной функции в виде
Ws C
C
s s
C
s s
C
s s
j
j
k j
j
k
Nj
Nj
kN j
j
kN
j
j
j N
n
()
( ) ( )
.= +
−
+
−
+
−
−+
=
−+
= = +
∑ ∑ ∑
0
1
1
1 1
1
1
1
1 1
Коэффициенты C
ij
вычисляются по вычетам в кратных полюсах. Например,
для k1-кратного полюса s
1
C
j
d
ds
s s
Bs
As
j
s s
j
k
1
1
1
1
1
1
1
=
−
−
→
−
( )!
lim ( )
()
()
.
Обозначим компоненты вектора состояния для кратного полюса s
1
X s us s s
X X s s
X X s s
k
k k
1 1
11 1 1
1 2 1
() ()/( ),
/( ),
...
/( ).
=
−
= −
= −
−
Формирование компонент (рис.3.8)
представляется последовательным
соединением звеньев. Матрицы А, В, С
соответственно равны:
A
s
s
s
s
s
B
m
n
=
=
1 0 0
0 1 ... 0
0 0 0 . 0
...
0 ... .0
...
0 ...
1
1
1
0
0
1
1
1
, ...
...
,
(3.11)
C=[C
1,1
...C
1,k1
,..., C
N,1
...C
N,kN
, C
N+1
...C
n
].
31
Уравнение формирования выходного сигнала y(t)=C
0
u(t)+CX(t).
Пример. Передаточная функция ДПИ имеет вид
Ws
s s
s
s
s
s
s
()
, ,
.=
+ +
+
+
+
+
+
2
5 4 3 2
08 012
14
75
194
244
120
Вычисляем полюсы передаточной функции и коэффициенты элементарных
дробей (вычеты). Полюсы: s
11
=-2, s
12
=-2, s
13
=-2, s
2
=-5, s
3
=-3. Вычеты для
кратных и простых полюсов: для полюса s
1
=-2 C
11
=0,84, C
12
=-2,19,
C
13
=2,97; для полюса s
2
=-5 С
2
=0,39; для полюса s
3
=-3 С
3
=-0,336. Полюсы
отрицательные, действительные, что соответствует устойчивому объекту
наблюдения. Действительность нулей и полюсов позволяет сформировать
матричную модель ДС путем разложения передаточной функции на сумму
простых дробей. С учетом найденных полюсов и коэффициентов разложения
получим разложение передаточной функции
Ws
s s
s s s
()
,
( )
,
( )
, , ,
.=
+
−
+
+
+
+
+
−
+
084
2
219
2
297
2
039
5
0336
3
3 2
Коэффициент С
0
=0. Уравнения для компонент вектора X:
x′
1
=-2x
1
+x
2
,
x′
2
=-2x
2
+x
3
,
x’
3
=-2x
3
+u (t), x′
4
=-5x
4
+u(t), x′
5
=-3x
5
+u(t).
Матрицы А, В, С из (3.11) соответственно равны
A B=
=
-2 1 0 0 0
0 -2 1 0 0
0 0 -2 0 0
0 0 0 -5 0
0 0 0 0 -3
, ,
0
0
1
1
1
C=[0,84 -2,19 2,97 0,39 -0,336].
Имеем выходной сигнал y(t)=0,84x
1
-2,19x
2
+2,97x
3
+0,39x
4
-0,336x
5
.
3.2.5. Метод представления передаточной
функции произведением дробей
Корни характеристического полинома должны быть действительными.
Передаточная функция при этом разлагается на произведение простых дробей
[5]
Ws
Bs
As
b bs bs
a as as
K
s p
s s s s
m
m
n
n
j
j
j
m
j
jm
n
()
()
()
...
...
.= =
+ + +
+ + +
=
−
− −
= = +
∏ ∏
0 1
0 1 1 1
1
где
K
b
a
m
n
=
. Учитывая тождество
s p
s s
s p
s s
j
j
j j
j
−
−
=+
−
−
1 ,
составим

32
структурную схему для передаточной функции (рис.3.9).
Рис.3.9
Уравнения состояния в этом случае приобретают вид
x sx s put
x sx s p x s put
x sx s p x x ut
x x x s x ut
x x s x
x x sx
m mm m m m
m m m m
m m m m
n n nn
1 11 1 1
2 22 2 2 1 2 2
1 1
1 1 1 1
2 1 2 2
1
'
'
'
'
'
'
( )(),
( ) ( )(),
...
( )( ... ()),
... (),
,
...
.
= + −
= + − + −
= + − + + +
= + + + +
= +
= +
−
+ + +
+ + + +
−
Уравнение выхода y(t)=Kx
n
.
В матричном виде система уравнений следующая
X
X
X
X
X
s
s p s
s-p s-p s
s
s
X
X
X
X
m
m
n
m m m m m
m+
n
m
m
1
2
1
1
2
1
1
2
'
'
...
'
'
...
'
'
'
...
'
+ +
=
−
0 ... 0
0 ... 0
...
... 0 ... 0
1 ... 1 1 ...0
...
0 .. . 1
2 2
1
1 1
2
1'
....
'
...
...
().
X
s p
p
ut
n
+
−
−
s
s -p
0
2
m m
(3.12)
Матрица С имеет вид C=[0, 0,...,K].
Пример. Передаточная функция ДПИ W(s)=(2s+12)/(3s
2
+24s+21).
Вычислим нули и полюсы передаточной функции: p
1
=-6, s
1
=-1, s
2
=-7.
Полюсы передаточной функции отрицательные, действительные, что
соответствует устойчивой динамической системе. Действительность нулей и
полюсов позволяет сформировать матричную модель ДС путем разложения
передаточной функции на произведение простых дробей:
Ws
b
a
s p
s ss s
s
s s
m
n
() , .=
−
− −
=
+
+ +
1
1 2
1
066
6
1
1
7
33
Уравнения для компонент вектора X в этом случае имеют вид
x′
1
=-x
1
+5u(t), x′
2
=-7x
2
+x
1
.
Уравнение выходного сигнала y=0,66x
2.
Матричный вид системы уравнений
по (3.12)
[ ]
x
x
x
x
ut C
'
'
(), .
1
2
1
2
1 5
0
0
=
−
+
=
0
1 -7
0,66
Результаты проектирования показывают, что матричная модель ДС
является универсальной, дискретное представление удобно для цифрового
моделирования на ПЭВМ, так как алгоритм моделирования не меняется при
изменении исходных данных.
3.3. Статистическое моделирование систем
Метод статистических испытаний, или метод Монте-Карло (МК), - это
численный метод решения математических задач при помощи моделирования
случайных величин. Этот метод позволяет исследовать любой процесс, на
протекание которого влияют случайные факторы. Для задач, не связанных со
случайностями, можно искусственно придумать вероятностные модели [23].
Общая схема применения метода состоит в том, что функцию, которую
нужно вычислить, представляют в виде математического ожидания f(x
1
,...,x
n
)
от n независимых случайных величин. Используя n случайных чисел,
моделируемых датчиками случайных чисел, получим реализацию функции.
Следующие n случайных чисел дают реализацию, независимую от
предыдущей, и т.д. Набрав достаточное число реализаций, в качестве
приближенного значения оцениваемой функции принимают среднее
арифметическое по реализациям. Среднеквадратическая погрешность
полученной статистической оценки с ростом числа реализаций N убывает
пропорционально 1/N
2
.
При статистическом моделировании систем производится
воспроизведение процессов, происходящих в системах, с искусственной
имитацией случайных величин, от которых зависят эти процессы, с помощью
датчиков случайных чисел. Комбинируя детерминированные и
стохастические зависимости, составляют алгоритм моделирования системы.
Применяя его, получают независимые реализации процесса в заданных
условиях использования системы. Характеристики, которые нужно
определить, оцениваются методом МК. Алгоритм моделирования
используется как для анализа, так и для оптимизации и синтеза систем.
34
3.3.1. Статистические испытания системы массового обслуживания
Система массового обслуживания (СМО) - это система, которая имеет
целью решение однотипных задач, поступающих в нее в виде запросов
(заявок). Система массового обслуживания имеет n каналов для
обслуживания, каждый из которых характеризуется временем обслуживания
(временем решения задачи). Моменты поступления запросов случайные. В
простейшем случае задача ставится по определению, сколько в среднем
заявок обслужит СМО за время Т и сколько она даст отказов [24].
Алгоритм функционирования СМО.
Исходными данными при испытаниях являются: Roj - время
обслуживания заявки в j-м канале (при однотипных каналах среднее время
обслуживания во всех каналах одинаково); Тc - общее время работы СМО в
одном статистическом испытании; закон формирования случайного времени
поступления заявки. Обозначим: Со, Сн - счетчики обслуженных и
необслуженных заявок; Rк - отрезок времени, через который поступает
очередная заявка относительно предыдущей; t
j
- момент времени
освобождения j-го канала после обслуживания находящейся в нем заявки; Тк
- момент поступления очередной заявки в СМО. Структурная схема
алгоритма функционирования СМО представлена на рис.3.10.
В начале работы СМО все каналы свободны, значит, t1=t2=,...,tn=0;
момент поступления заявки Т1=0. Первая заявка поступает на канал n1, и
этот канал в течение Ro1 будет занят, поскольку время его работы
t1=T1+Ro1. Так как первая заявка обслуживается, то к счетчику
выполненных заявок добавляется 1 (Со=Со+1). Затем СМО производит
обслуживание следующих заявок. Предположим, что k-1 заявок уже
рассмотрены, тогда вычисляется (разыгрывается) случайный период
поступления k-й заявки - Rк и вычисляется момент времени поступления k-й
заявки Тк=Тк-1+Rк. Свободен ли в данный момент времени какой-либо
канал обслуживания ?. Проверка этого условия производится
последовательно в цикле в пределах общего количества каналов. Свободный
канал j занимается поступившей заявкой. В этом случае вычисляется время
освобождения канала tj=Tк+Roj и добавляется 1 к счетчику выполненных
заявок Со=Со+1, затем процесс моделирования обслуживания заявок
повторяется.
35
Рис.3.10
Если нет свободного канала, то добавляется 1 к счетчику отказов
Сн=Сн+1 и опять производится моделирование очередной заявки. В процессе
моделирования очередной заявки проверяется время окончания работы СМО
Тк>Тс, и, когда это условие оказывается выполненным, отдельный опыт
статистического моделирования СМО заканчивается. Такой опыт повторяется
N раз, затем производится статистическая обработка результатов. Основные
показатели работы СМО индицируются на экране дисплея в виде гистограмм
или графиков. В ходе статистических испытаний может быть произведено
изменение характеристик СМО (число каналов, среднее значение и дисперсия
времени обслуживания j-го канала, характеристики потока заявок -
интенсивность и др.).
Рассмотрен алгоритм моделирования и статистических испытаний
простейшей СМО. На практике встречаются модели более сложных СМО.
Как правило, время обслуживания в реальных СМО в каждом канале имеет
свои характеристики (среднее значение, дисперсию, закон распределения).
Имеют место также СМО с ожиданием, где отказ выдается не сразу, а заявка
ставится в очередь при условии, что есть надежда на ее обслуживание до
окончания времени опыта. Учитываются среднее время обслуживания и
размер очереди, случайный выход из строя отдельных каналов и случайное
36
время восстановления отказавшего канала, а также интенсивности потока
заявок во времени.
n-канальная СМО с отказами обслуживания.
Это классическая задача теории массового обслуживания - задача Эрланга
[24]. Пусть имеется n-канальная СМО, на которую поступают заявки с
интенсивностью L; поток обслуживаний имеет интенсивность M, обратную
среднему времени обслуживания заявки to. Обозначим p=L/M - приведенная
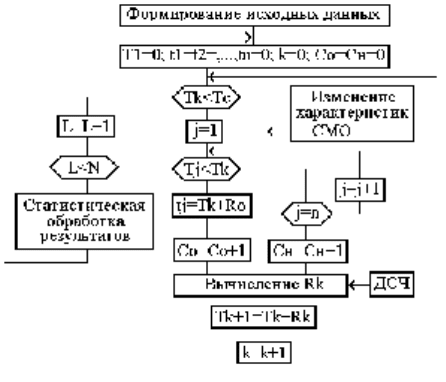
интенсивность потока заявок. Граф состояний СМО представлен на рис.3.11.
Рис.3.11
Характеристики эффективности данной СМО следующие:
p0, p1,...,pk - вероятности состояний СМО (при p<1):
p p
p p
k
p
n
k n
0 1
2
2
1
= + + + + + +
−
!
,...,
!
,...,
!
,
p pp pk
p
k
p pn
p
n
p
k n
1 0 0 0= = =,...,
!
,
!
;
Po - вероятность того, что поступившая заявка получит отказ (все каналы
заняты):
Po pn
p
n
p
n
= =
!
;0
Q - относительная пропускная способность СМО - вероятность того, что
заявка будет обслужена:
Q Po
p
n
p
n
=− =−1 1 0
!
;
А - абсолютная пропускная способность СМО получается при умножении
интенсивности потока заявок L на Q:
A=LQ L
p
n
p
n
= −
1 0
!
;
k - среднее число занятых каналов равно математическому ожиданию
дискретной случайной величины с возможными значениями 0,1,..., n и
вероятностями этих значений p0, p1,...,pn:
37
k=
A
M
p
p
n
p
n
= 1 0−
!
.
Одноканальная СМО с неограниченной очередью.
Пусть имеется одноканальная СМО с очередью, на которую не
наложено никаких ограничений (ни по длине очереди, ни по времени
ожидания). На эту СМО поступает простейший поток заявок с
интенсивностью L; поток обслуживаний имеет интенсивность M, обратную
среднему времени обслуживания заявки to. Обозначим p=L/M - приведенная
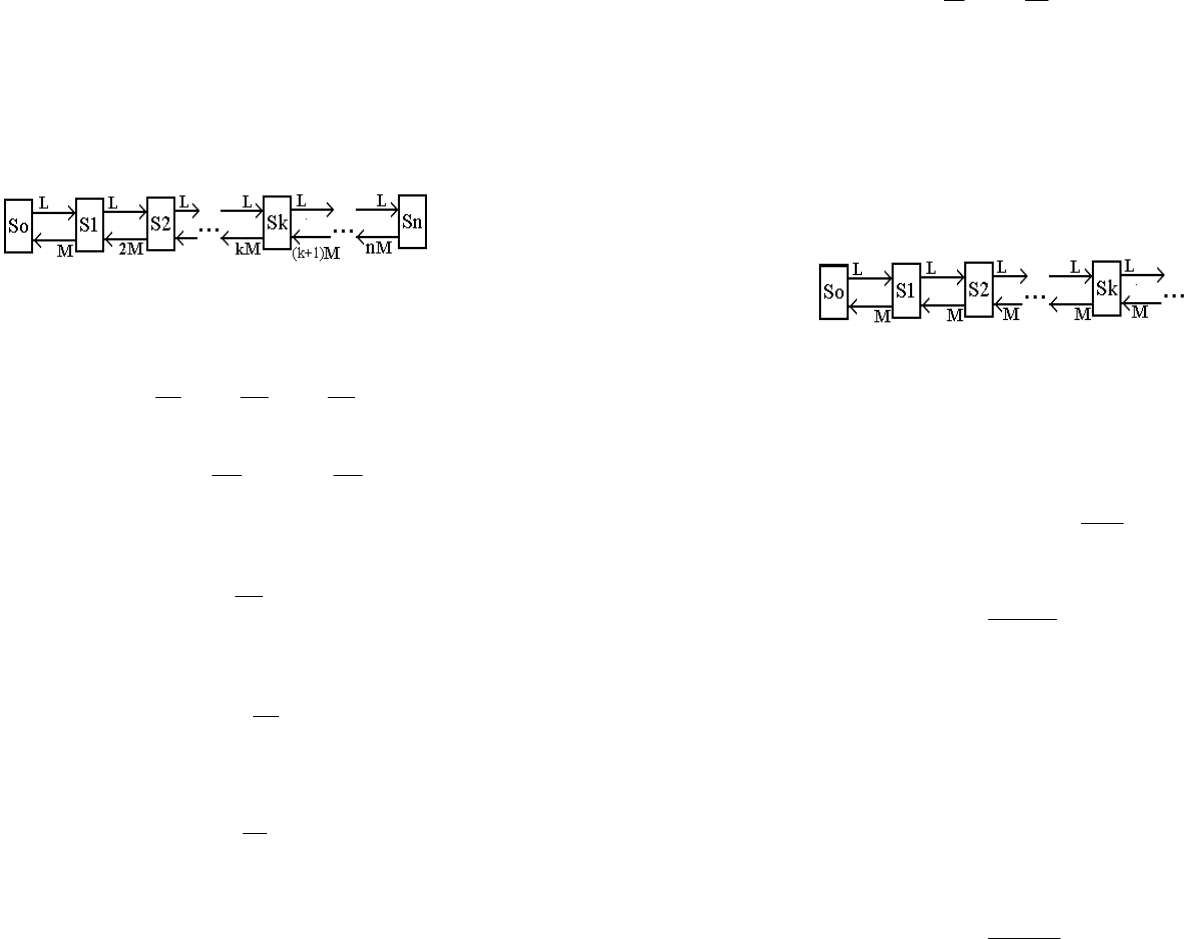
интенсивность потока заявок. Граф состояний СМО изображен на рис.3.12.
Рис.3.12
Характеристики эффективности данной СМО следующие:
p0, p1,...,pk - вероятности состояний СМО (при p<1):
p p p p p pk p p
k
0 1 1 1 1=− = − = −, ( ), ( );
Zc - среднее число заявок в системе:
Zc Mk kp
p
p
k
k
= = =
−
=
∞
∑
[] ;
0
1
Wc - среднее время пребывания заявки в системе по формуле Литтла:
Wc
L p
=
−
1
1( )
;
Zо - среднее число заявок в очереди: Zо=Zc-Z
oб
, где Zc - среднее число
заявок в системе; Z
oб
- среднее число заявок под обслуживанием. Число
заявок под обслуживанием в данной СМО может быть либо нулем (если
канал свободен), либо единицей (если канал занят). Математическое
ожидание (среднее значение Z
oб
) равно вероятности Pз того, что канал занят
(степень загрузки канала). Очевидно, что Pз=1-p0=p, где p0 - вероятность
того, что канал свободен. Следовательно, среднее число заявок под
обслуживанием Z
oб
=p, отсюда имеем Zo=Zc-Z
oб
=p/(1-p)-p=p
2
/(1-p);
Wо - среднее время пребывания заявки в очереди по формуле Литтла:
Wo
p
L p
=
−
2
1( )
;

38
А - абсолютная пропускная способность СМО: А=L, так как очередь не
ограничена и каждая заявка рано или поздно будет обслужена;
Q - относительная пропускная способность СМО: Q=1 также ввиду того,
что очередь не ограничена и каждая заявка будет обслужена.
3.3.2. Математическое обеспечение статистических испытаний
Пакет программ МК предназначен для проведения статистических
испытаний СМО и исследования качества стохастических систем.
Существуют трудности реализации метода статистических испытаний.
Стремление к достаточно адекватной модели системы для статистических
испытаний значительно увеличивает время моделирования в связи с
громоздкими, часто повторяющимися вычислениями.
Метод МК требует постоянного обращения к датчикам случайных чисел
(ДСЧ). Каждое обращение занимает длительное время (от микросекунд до
десятков миллисекунд, в зависимости от типа ПЭВМ). Таких обращений к
ДСЧ при моделировании достаточно реальных моделей систем может быть
миллионы. Сократить время, затрачиваемое на это, можно путем
предварительного накопления случайных чисел в некотором
вспомогательном массиве с последующей подкачкой из таблицы случайных
чисел с жесткого магнитного диска. Чтение очередного блока чисел с
магнитного диска (2000...5000) выполняется значительно быстрее, чем
вычисление тех же чисел программным путем. Особенно это проявляется,
когда закон распределения отличается от равномерного.
При моделировании сложных систем можно выделить в них ряд более
простых подсистем (провести декомпозицию) и предварительно
промоделировать эти подсистемы, заменив их затем в общей системе
результатами моделирования (таблицами полученных случайных чисел). Эти
таблицы могут быть записаны на жесткий магнитный диск и при проведении
моделирования всей системы читаться в требуемой последовательности, что
существенно сокращает время моделирования сложной системы [25].
При большом числе факторов, влияющих на функционирование
исследуемой системы, необходимо предварительно оценить вклад каждого из
них в суммарную дисперсию выходных параметров и при малом влиянии
исключить их варьирование (моделирование как случайных величин).
Кроме больших затрат времени метод МК требует и накопления
значительных массивов статистической информации для ее последующей
39
обработки и анализа. Можно ″сбрасывать″ накапливаемую информацию
блоками на жесткий магнитный диск, можно также проводить рекуррентное
вычисление статистических характеристик в процессе моделирования и
записывать на диск только некоторые прореженные значения статистических
характеристик [26].
Рекуррентное вычисление статистических характеристик особенно
необходимо при текущей индикации результатов статистических испытаний
на экране дисплея.
3.3.2.1. Моделирование процессов с заданным законом распределения
Любой язык программирования высокого уровня имеет программу-
функцию, дающую равномерно распределенную случайную величину в
диапазоне [0,1]. На основании этой величины формируются другие с
требуемым законом распределения и числовыми характеристиками [9].
Для получения случайной величины Е, распределенной в диапазоне [a,b] с
плотностью f(x), необходимо решить интегральное уравнение
fxdx q
a
b
() ,=
∫
где q - равномерно распределенная величина в диапазоне [0,1].
Для равномерно распределенной случайной величины Е в диапазоне [a,b]
плотность вероятности имеет вид
fx
b
a
()=
−
1
при a<x<b, а интегральное
уравнение относительно Е
1
b a
dx q
a
E
−
=
∫
дает выражение Е=a+q(b-a).
Нормально распределенная случайная величина формируется из
равномерно распределенных на основании центральной предельной теоремы.
Например, в библиотеке программ на языке Фортран имеется подпрограмма
GAUSS [9], которая вычисляет нормально распределенную случайную
величину в виде
E q
j
j
= −
=
∑
1
6
6
, где q
i
- равномерно распределенная
случайная величина в диапазоне [0,1], имеющая математическое ожидание m
и дисперсию σ
2
. Для получения нормально распределенной случайной
