Wai-Fah Chen.The Civil Engineering Handbook

Подождите немного. Документ загружается.

Simulation in Hydraulics and Hydrology 38-33

the Runoff Block is the origin of water quality constituents. The Runoff Block attempts to simulate the

buildup of pollutants on the watershed and the overland transport of these pollutants into the drainage

system. The mechanisms of urban runoff quality involve factors such as wind, erosion, trafﬁc, atmospheric

fallout, land surface activities, street cleaning, and many other complex processes. XP-SWMM attempts

to consider many of these factors; however the difﬁculties of modeling urban runoff quality are well

documented and cannot be completely overcome by XP-SWMM.

Water quality can be simulated in three different ways in the Runoff Block: (1) Buildup and Washoff,

(2) Rating Curve, and (3) Event Mean Concentration. The Buildup and Washoff method simulates

buildup of dust and dirt on the watershed as well as the subsequent washoff using exponential functions.

The second method is the use of a rating curve of concentration vs. ﬂow rate. The third method for

simulating water quality is using the event mean concentration (EMC). The Runoff Block can also include

water quality constituents in rainfall, catchbasin ﬂushing, and erosion of solids using the Universal Soil

Loss Equation.

Pollutants generated by the Runoff Block enter the drainage system as a pollutograph at the nodes,

which are shared by the Runoff and EXTRAN Block (the same way hydrographs enter the system).

Pollutographs may also be generated and enter the drainage system in the EXTRAN Block by simulating

dry weather ﬂow for simulation of combined sewer systems. Once in the sewer network, each pollutant

is individually routed through conduits in the EXTRAN Block by assuming complete mixing within the

conduit in the manner of a continually stirred tank reactor (CSTR). With this assumption, the concen-

tration of the pollutant leaving the pipe is equal to the concentration in the pipe. All subsequent

calculations are thus based on a mass balance, with pollutants being added or removed based on the

concentration in the conduit. These calculations include scour, deposition, and decay of each pollutant.

XP-SWMM Example Problem

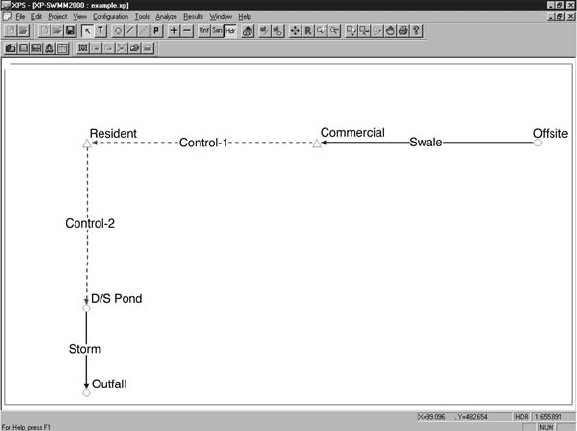
A simple XP-SWMM example watershed is shown in the following schematic (Fig. 38.19).

RUNOFF Block

The watershed will be analyzed using the National Resource Conservation Service (NRCS) TR-55 meth-

odologies and Illinois State Water Survey (ISWS) Bulletin 70 rainfall depths and the Huff 3

Quartile

design rainfall distribution. The watershed is broken into three subbasins as shown in Table 38.12.

FIGURE 38.19 Sample XP-SWMM model schematic.

38-34 The Civil Engineering Handbook, Second Edition

This information is entered into the Runoff Block of the XP-SWMM model at the appropriate node.

A hydrograph will be generated at these three “active” nodes in the Runoff Block based on this information

in Table 38.12 using the NRCS methodology. In this example, the Huff 3rd Quartile design rainfall

distribution and ISWS Bulletin 70 100-year 24-hour rainfall depth are entered in the Global Data database

and are referenced at each node in the Runoff Block. A starting and ending date and time must be selected

for a model run. For this example, the time period selected is July 18, 2001 to July 21, 2001.

EXTRAN Block

This watershed consists of farmland in the headwaters and commercial and residential development in

the downstream areas. The offsite area drains via open swale to the commercial area. A cross-section,

length, channel roughness, channel slope, bank stations, and upstream and downstream inverts of the

swale are entered into this link to route the offsite ﬂow to the commercial area. The commercial area

drains into a stormwater detention basin, which drains to a residential area that is also served by a

stormwater detention basin. The storm sewers within the commercial and residential area have been

omitted from this example, for it can be reasonably assumed that all of the runoff in these areas drains

to the detention basins via storm sewers and overland ﬂow routes with little attenuation. These runoff

processes can be simulated in the Runoff Block.

The stormwater detention basins for the commercial and residential areas are represented by a triangle

in XP-SWMM. An elevation-area relationship is entered at the commercial and residential nodes in the

EXTRAN Block. The control structure for each detention basin, represented by a dashed multi-conduit

in the EXTRAN block, is composed of an oriﬁce and an overﬂow weir. The relevant hydraulic properties

(elevation, area, discharge coefﬁcient, length) of the weir and oriﬁce are explicitly entered into each multi-

conduit. The residential detention basin drains into a storm sewer. Pipe size and shape, roughness, length,

slope, rim, and invert elevations are entered for each storm sewer. The downstream side of this storm

sewer is considered the outfall of the system. Several options exist for outfall conditions, but this example

will use a critical depth assumption.

Results

XP-SWMM presents results in tabular and graphical formats. Tabular output of numerous hydrologic

and hydraulic input parameters and results may be speciﬁed within XP-SWMM. This output can easily

be imported into spreadsheets for further analysis or graphing. However, the graphical capabilities of

XP-SWMM allow for the user to view discharge hydrographs of all links and stage hydrographs of all

nodes within XP-SWMM in the EXTRAN Block. Furthermore, runoff discharge hydrographs at each

node may also be viewed in the Runoff Block.

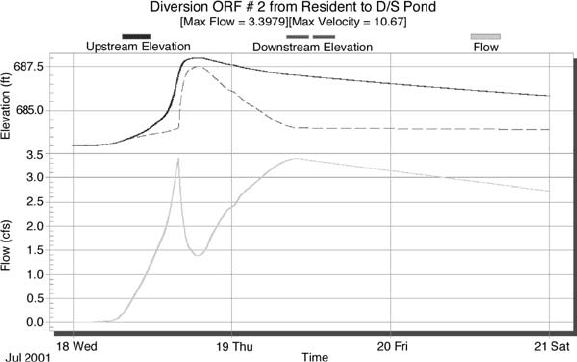
Figure 38.20 shows the discharge hydrograph of the oriﬁce in the control structure for the residential

development. The upstream elevation represents the water surface elevation in the residential stormwater

detention basin. The downstream elevation represents the water surface elevation downstream of the

residential stormwater detention basin control structure. In this example, the tailwater effect on the oriﬁce

from the downstream node can be clearly seen by the sharp drop in the hydrograph as the downstream

water surface elevation rises.

This graph may also be exported from XP-SWMM in a tabular format that can be imported into

spreadsheet programs for further analysis. XP-SWMM also produces an output ﬁle for each model run

that gives details of the hydrologic and hydraulic simulation.

TABLE 38.12 Hydrologic Model Subbasin Parameters

Subbasin Name

Area

(acres)

Runoff Curve

Number

Time of Concentration

(minutes)

Offsite 150 72 240

Commercial 20 94 15

Residential 40 83 45

Simulation in Hydraulics and Hydrology 38-35

References

Barkau, R.L. 1992. UNET, One Dimensional Unsteady Flow through a Full Network of Open Channels,

Computer Program, St. Louis, MO.

Bedient, P.B. and Huber, W.C., 1988. Hydrology and Floodplain Analysis. Addison-Wesley, Reading, MA.

Burke, C.B. and Burke, T.T. Jr., 1994. Stormwater Drainage Manual. Te ch Rept. H-94–6. Highway Exten-

sion and Research Project for Indiana Counties and Cities, Purdue University, West Lafayette, IN.

Hoggan, D.H., 1989. Computer Assisted Flood Plain Hydrology and Hydraulics. McGraw-Hill, New York.

Huber, W.C. and Dickinson, R.E., 1988. Storm Water Management Model, Version 4: User’s Manual.U.S.

Environmental Protection Agency, Athens, GA.

Huff, Floyd A. and Angel, James R., 1989. Frequency Distributions and Hydroclimatic Characteristics of

Heavy Rainfall in Illinois. Illinois State Water Survey, ISWS/BUL-70/89.

Hydrologic Engineering Center, 1983. HECDSS User’s Guide and Utility Program Manual, U.S. Army

Corps of Engineers, Davis, CA.

Hydrologic Engineering Center, 1990. HEC-1 Flood Hydrograph Package, User’s Manual, U.S. Army Corps

of Engineers, Davis, CA.

Hydrologic Engineering Center, 2001. HEC-RAS River Analysis System, User’s Manual, Version 3.0, U.S.

Army Corps of Engineers, Davis, CA.

Hydrologic Engineering Center, 2001. Hydrologic Modeling System HEC-HMS, User’s Manual, Version

2.1, U.S. Army Corps of Engineers, Davis, CA.

NRCS, 1982. TR-20 Computer Program for Project Formulation Hydrology, Te ch Release No. 20, Wash-

ington, D.C.

Further Information

Barkau, R.L., 1992. UNET, One Dimensional Unsteady Flow through a Full Network of Open Channels,

Computer Program, St. Louis, MO.

Bedient, P.B. and Huber, W.C., 1988. Hydrology and Floodplain Analysis. Addison-Wesley, Reading, MA.

Singh, V.P., 1995. Computer Models of Watershed Hydrology, Water Resources Publications, Highlands

Ranch, CO.

FIGURE 38.20 XP-SWMM graphical output.

Water Resources

Planning and

Management

39.1 Introduction

Water Resources Decision Making • Water Resources Modeling •

Optimization vs. Simulation Models • Deterministic vs.

Stochastic Models • Static vs. Dynamic Models • Investment vs.

Operations/Management Models • Lumped vs. Distributed

Data Models

39.2 Evaluation of Management Alternatives

39.3 Water Quantity Management Modeling

Deterministic Reservoir Models • Reservoir Storage

Requirements • Flood Control Planning • Water Supply

Objectives • Power Production Objectives • Flow Augmentation

and Navigation • Real-Time Operations • System Expansion •

Stochastic Reservoir Modeling • Water Quality Modeling •

Groundwater Modeling

39.4 Data Considerations

39.1 Introduction

Water resources planning and management engineering is concerned with conceptualizing, designing,

and implementing strategies for delivering water of sufﬁcient quality and quantity to meet societal needs

in a cost-effective manner. Alternatives that can be engineered to accomplish these functions include

development of new water supplies, regulation of natural sources of water, transfer of water over large

distances, and treatment of degraded water so that it can be reused. The challenges for water resources

engineers are: (1) to identify the essential characteristics of a given water resources problem, (2) to identify

feasible alternatives for resolving the problem, (3) to systematically evaluate all feasible alternatives in

terms of the goals and objectives of the decision makers, and (4) to present a clear and concise repre-

sentation of the trade-offs that exist between various alternatives.

Water Resources Decision Making

Because large-scale planning, development, and management of water resource systems generally take

place in the public sector, the individual responsible for making decisions about, or selecting from, a set

of development alternatives is usually not the engineer(s) who perform the technical analyses related to

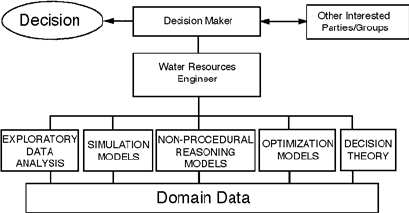
the given problem domain. The decision-making topology is rather more like that presented in Fig. 39.1.

At the top of the topology is the decision maker, usually an elected ofﬁcial or his or her appointee. This

individual assumes the responsibility for selecting a course of action that best achieves the goals and

J.R. Wright

University of California, Merced

M.H. Houck

George Mason University

-2

The Civil Engineering Handbook, Second Edition

objectives of his or her constituency. During the course of the decision-making process, the decision

maker interacts with other interested parties, such as local, state, and federal government agencies; non-

governmental organizations and groups; industry; and individuals.

At the bottom of the hierarchy are all data that pertain to the problem domain, including hydrologic

data, economic and other cost data, demographic and historic data, and information about relevant

structural and management technologies. The water resources engineer selects, from a wide range of

modeling and analysis technologies, those that can best evaluate these data and provide the decision

maker with information about the trade-offs that exist among and between multiple and conﬂicting

management objectives. In addition, the water resources engineer may interact with other interested

parties, including social scientists, economists, and environmentalists, to ensure a comprehensive con-

sideration of the system and its impacts. Consequently, the water resource systems analyst must be skilled

in problem identiﬁcation; proﬁcient in the use of different modeling methods and technologies; and

willing and able to interact with technical, and non-technical managers and decision makers.

Comprehensive water resource, planning and management is generally conducted in several separate

but related phases requiring input from a wide range of specialists including urban and regional planners,

economists and ﬁnancial planners, government agency personnel, citizen groups, architects, sociologists,

real estate agents, civil engineers, hydrologists, and environmental specialists. The National Environmen-

tal Policy Act of 1969 (NEPA) requires the preparation of an environmental impact statement for every

major federal action (program, project, on licensing action) “signiﬁcantly” affecting the quality of the

human environment. Most water projects fall under this legislation and most states have prepared regional

guidelines for complying with NEPA. Special-purpose developments often require the assistance of

specialists from disciplines such as soil scientists, agricultural specialists, crop experts, computer special-

ists, and legal experts. These individuals are involved in one or more of several planning and management

phases

• Establishment of project goals and objectives

•Collection of relevant data

•Identiﬁcation of feasible best-compromise alternative solutions

•Preliminary impact assessment

•Formulation of recommendation(s)

•Implementation (detailed structural design, construction, and/or policy implementation)

•Operation, management, and sustainment

Because most large-scale water resources projects involve many different constituencies having different

goals and objectives, a multiobjective perspective through this process is essential. Consider, for example,

the problem of developing an operating strategy for a large multipurpose reservoir designed to provide

water for irrigated agriculture, municipal and industrial water supply, water-based recreation, and power

FIGURE 39.1

The water resources engineer uses a wide range of analytical tools and techniques to identify and

evaluate alternative development plans and management strategies. The selection of a particular project or plan from

a set of alternatives identiﬁed by the engineer is the responsibility of the decision maker.

Water Resources Planning and Management

-3

generation (see Chapter 37 for a comprehensive discussion of water resource structures). The reservoir

may also be a critical component in a regional ﬂood control program. The decision maker in this context

might be a regional water authority which reports to a state water agency or to the state governor. Clearly,

the decision maker has responsibilities to a range of constituencies that might include the citizens at

large, industry special interest groups, the environment and future generations, and perhaps a present

political administration. The operating strategy that best meets the needs of one interest may prove

disastrous for another. (For a thorough discussion of multiple and conﬂicting objectives in water resources

planning and management, see Cohon and Rothley, 1997; Goodman, 1984; and Linsley et al., 1992.) The

selection among alternatives is thus the responsibility of the decision maker who represents these groups.

The role of the engineering analyst is to develop a clear and concise documentation of feasible alternatives.

The focus of this chapter is the use of analytical engineering management tools and techniques for

developing these alternatives.

Water Resources Modeling

The main tool of the water resources engineer is the computer model, which can be classiﬁed by:

(1) structure and function (optimization or simulation), (2) degree of uncertainty in system inputs

(deterministic or stochastic), (3) level of ﬂuctuation in economic or environmental conditions being

modeled (static or dynamic), (4) distribution of model data (lumped or distributed), and (5) type of

decision to be made (investment or operations/management). Each model conﬁguration has inherent

strengths and weaknesses, and each has its proper role in water resources planning. The challenge for

the water resources engineer is not to determine which is better, but which is most appropriate for a

particular situation given available resources including time, money, computer capability, and data.

Optimization vs. Simulation Models

A variety of water resources management and planning models can be formulated and solved as opti-

mization models. Optimization models have the following general structure:

(39.1)

Subject to:

(39.2)

(39.3)

…

(39.4)

(39.5)

Equation (39.1) is called the objective function and is speciﬁed as a mathematical criterion for

measuring the ‘goodness’ of any given solution. The objective function is a function of a set of non-neg-

ative variables known as decision variables (

, x

, …, x

), which typically represent the choices available

to the decision makers. The optimal solution to the optimization model is the set of values of the decision

variables that provides the “best” (e.g., maximum or minimum) value for the objective function.

The quality of the solution as measured by the objective function is constrained by a set of equations,

appropriately called constraint equations or constraints — Eqs. (39.2–39.4) above. The constraints

Optimize Zfxx x

=º

()

,,,

gxx x b

n11 2 1

,,,º

()

gxx x b

n21 2 2

,,,º

()

gxx x b

mnm12

,,,º

()

≥ =º012 , , , J

-4

The Civil Engineering Handbook, Second Edition

represent all the real-life restrictions on the values of the decision variables. The functions

, g

, … g

depend on the values of the decision variables, and are restricted to be less-than-or-equal-to a set of

constants

, b

…

, b

. This is the typical presentation of an optimization model; however, equalities and

greater-than-or-equal-to inequalities in the constraints are allowed.

Finally, the optimization model typically includes the requirement that all decision variables are non-

negative — Eq. (39.5). From an engineering management standpoint, decision variables represent those

factors of a problem over which the engineer has control, such as the amount of resource to allocate to

a particular activity the appropriate size of a component of a structure, the time at which something

should begin, or cost that should be charged for a service. Clearly negative values for such things have

no physical meaning. However, if there are decision variables that should be allowed to take on negative

values, then this can be accommodated within an optimization model.

If a water resources planning or management model can be constructed to adhere to the rigid structure

of the optimization model, a variety of solution methodologies are available to solve them [Hillier and

Lieberman, 1990; Sofer and Nash, 1995]. These techniques are continuously improving in scale and

efﬁciency with the ongoing improvements in information technology (e.g., object oriented programming,

increasing computational speeds of computer processors). New techniques such as artiﬁcial neural net-

works, or evolutionary computing — an offshoot of artiﬁcial intelligence — are offering an even greater

range of solution options (e.g., Wardlaw and Sharif, 1997).

Undoubtedly the most widely used analytical procedure employed in the area of water resources

systems engineering is simulation (or descriptive) modeling. The main characteristics of this modeling

methodology are: (1) problem complexities can be incorporated into the model at virtually any level of

abstraction deemed appropriate by the model designer or user (in contrast to the more rigid structure

required by optimization models), and (2) the model results do not inherently represent good solutions

to engineering problems. These models reﬂect the structure and function of the system being modeled

and do not attempt to suggest changes in design or conﬁguration towards improving a given scenario.

Simulation models may be time or event sequenced. In time-sequenced simulation, time is represented

as a series of discrete time steps (

= 0, 1, 2,…,

) of an appropriate length perhaps hours, days, weeks,

or months depending on the system being modeled. At the end of each time period

all model parameters

would be updated (recomputed) resulting in a new system state at the beginning of time step

+ 1. The

relationships among and between model parameters may be deterministic or stochastic through this

updating process, again depending on the design of the system and the level of abstraction assumed by

the model. Model inputs, both initially and throughout the simulation, may follow parameter distribu-

tions as discussed in the previous section or may be input from external sources such as monitoring

instrumentation or databases.

Models that simulate physical or economic water resource systems can also be event sequenced, wherein

the model is designed to simulate speciﬁc events or their impacts whenever they occur. These events

might be input as deterministic or stochastic events or they might be triggered by the conditions of the

system. In any case, the model responds to these events as they occur regardless of their timing relative

to simulated real time. Regardless of the treatment of time through the simulation process, these models

can be either deterministic or stochastic.

With increasingly powerful computer technology, extremely complicated simulation models can be

developed that emulate reality to increasingly high levels of accuracy. Very complicated systems can be

modeled through many time steps and these models can be “exercised” heavily (can be run many times

with different parameter settings and/or data inputs) to understand the system being modeled better. A

number of commercial vendors market simulation systems that can be used to design and develop

simulation models.

Historically, optimization models have been used as screening models in water resources planning and

management analyses. The gross level of abstraction required to “ﬁt’ a particular problem to this rigid

structure, coupled with the heavy computational burden required to solve these models, precluded the

construction of large and accurate systems representation. Once a general solution strategy or set of

alternatives was identiﬁed, simulation models could be constructed for purposes of more detailed analysis

Water Resources Planning and Management

-5

and “what-if” -type analyses. With the advent of increasingly powerful computing capability there is a

much tighter integration of these and other modeling technologies.

Deterministic vs. Stochastic Models

Water resources models can also be classiﬁed by the Ievel of uncertainty that is present in model

parameters and hydrologic inputs. A model is said to be deterministic if all input parameters and expected

future unregulated streamﬂows and other time series are assumed to be known with certainty and deﬁned

speciﬁcally within model constraint equations. If, on the other hand, only the probability distributions

of these streamﬂows are assumed to be known within the model, the model is said to be stochastic (see

Chapter 31 for a more complete discussion of statistical hydrologic analysis).

Both optimization and simulation models can be either deterministic or stochastic. Stochastic models

are generally more complex than deterministic models, having more variables and constraints or limiting

conditions. But deterministic models, having parameters and inputs based on average values over poten-

tially long time periods, are usually optimistic; system beneﬁts are usually overestimated, while costs and

system losses are generally underestimated. If sufﬁcient information and computational resources are

available, stochastic models (either optimization or simulation) are generally superior (Loucks et al.,

1981).

Static vs. Dynamic Models

Models vary in the manner in which changes to model parameters occur over time. In a particular

watershed, for example, while actual or predicted streamﬂows might vary over time, the probability

distribution for the streamﬂows may not change appreciably from one year to the next, and may thus

be considered static within the corresponding model. Dynamic models, on the other hand, assume

changing conditions over time and attempt to incorporate such changes into the analyses being conducted

(e.g., climate change models [Lane et al.

1999; Lettenmaier et al., 1999]). Dynamic models tend to be

more complex and require more computational effort to solve, but usually provide more accurate results,

assuming that adequate data are available to calibrate the models appropriately; this is particularly true

for investment models. Static models can be signiﬁcantly larger in scope. Models may be static in terms

of some factors (e.g., physical characteristics) but dynamic in terms of others (e.g., economies).

Investment vs. Operations/Management Models

Models may also be classiﬁed in terms of the time frame within which the analysis is being performed

and for which the resulting decision will be made. Long-term decisions dealing with selecting investment

strategies including things like physical changes to facilities (reservoir capacity expansion or hydroelectric

facility development, for example) are characteristically different from short-term decisions, such as

determining the appropriate reservoir release at a particular point in time. Models used to develop

operating or management strategies for a water resource system can generally be more detailed than

those designed to recommend longer-term investment decisions, which frequently consider actions taken

over multiple time periods.

Lumped vs. Distributed Data Models

Lumped data models are those that assume single values (e.g., average monthly rainfall or average

hydraulic conductivity for a 1 km

area) for parameters that might be represented better with a ﬁner

discretization of space or time. Distributed data models use a ﬁner resolution of parameters through

time or space (e.g., daily rainfall or hydraulic conductivity for each 100 m

area) to represent the same

system. Clearly, distributed data models require considerably more data and probably computational

effort while potentially providing a much more realistic representation of the physical system being

studied. Lumped parameter models are generally much more efﬁcient to solve and may be appropriate

-6

The Civil Engineering Handbook, Second Edition

in cases where insufﬁcient or incomplete data sources are available. With the explosive growth in the use

of geographic information systems and corresponding availability of spatial data, distributed data models

are becoming much more popular, at least within the research arena [Maidment, 1993].

39.2 Evaluation of Management Alternatives

For any given water resources problem, an alternative may be represented as a set of investment decisions,

each having a speciﬁc time-stream of costs and beneﬁts. The level of each investment is a variable, the

best value of which depends on the values of other variables and the goals and objectives of the decision

maker. Hence, each alternative may have many impacts that result in numerous economic gains and

losses (beneﬁts and costs) that occur at different times, different locations, and accrue to different

individuals or groups. The evaluation of the gains and losses associated with any particular alternative

may be complex. However, without this analysis, the selection of the best alternative will be impossible.

The questions that must be considered systematically by the water resources engineer in providing

meaningful guidance to the decision maker are: (1) how should each variable be evaluated economically?

(2) what is the set of values for these variables such that the resulting alternative best satisﬁes a given

objective? and (3) what is the best set of alternatives, and how can one be assured that there are no better

alternatives? A number of proven modeling techniques are available to address these questions.

Consider a set of alternate water resources projects

consisting of individual projects

. Each project

may be speciﬁed as a set of values for a discrete number of decision variables

= 1, 2, …,

. Each

project is fully speciﬁed by a vector of these decision variables and their values, represented by

. A

common goal of water managers is to identify that plan which maximizes net beneﬁts (NB):

(39.6)

When the beneﬁts (or costs) of a particular project alternative are most properly evaluated in economic

terms, the value of a particular investment component of any given project depends at least in part on

the timing of that particular investment. Because different water resources investment alternatives may

have different useful lives, it is important that they be compared using a common framework. While a

comprehensive treatment of engineering economic analysis is beyond the scope of this handbook, a brief

outline of an approach to valuing alternatives is offered. Basic understanding of the time value of money,

as well as ﬁnance principles, is important in an overall analysis of complex investment strategies. The

interested reader is referred to Jenkins et al. [2001]; Blanchard and Fabrycky [1990]; Fabrycky and

Blanchard [1991]; Grant et al. [1990]; and White et al. [1989] for additional information on performing

comprehensive engineering economic analysis.

Discount factors are used to determine the value of a particular investment over time.

Let PV = the present value of an amount of money (principal)

FV = the future value of an amount (or value) of money,

= the interest rate each period, and

= the life (in periods) of the investment.

Given an investment at the present time, the future value of that investment

time periods into the

future is given by the single-payment, compound-amount factor

(39.7)

The present value of costs (or beneﬁts) resulting from some future payment is computed using the

reciprocal of this factor, which is referred to as the single-payment, present-worth factor:

Maximize NB Xp

()

FV PV=+

()

1 i

Water Resources Planning and Management

-7

(

39.8)

Suppose that a particular investment (water resources project, for example) is anticipated to return a

stream of future net beneﬁts NB

over

discrete time periods,

= 1, 2, …,

. The present value of this

stream of beneﬁts is computed:

(39.9)

It is also possible to represent the present value of net beneﬁts (PV) of a project as an equivalent

uniform or constant stream of net beneﬁts over a horizon of T periods. Let A equal a constant amount

of money each period. Then,

(39.10)

where CR is the capital recovery factor deﬁned as:

(39.11)

As a supplement to using present value of net beneﬁts as a criterion to evaluate projects, the compu-

tation of a beneﬁt-cost ratio — present value of beneﬁts (PVB) divided by present value of costs (PVC) —

is often used to perform preliminary screening of alternatives:

(39.12)

Alternatives having a beneﬁt-cost ratio less than 1.0 should be removed from further consideration.

However, because costs are typically easier to identify and estimate, care should be used in itemizing and

valuing project beneﬁts for this purpose.

For public investments, the appropriate interest rate to be used in comparing projects is a matter of

public record and is based on the average yield on federal government bonds having approximately the

same maturity period, the economically useful life of the project being evaluated [Water Resources

Development Act of 1974 (P.L. 9302511)]. The assumption of a constant interest rate is standard practice

for these types of investments. A comprehensive discussion of inﬂationary considerations in project

evaluation is presented in Hanke et al. [1975].

39.3 Water Quantity Management Modeling

Among the largest public investments are those designed to stabilize the ﬂow of water in rivers and

streams. A stream that may carry little or no water during a signiﬁcant portion of the year may experience

extremely large (perhaps damaging) ﬂows during peak periods. A storage reservoir may be employed to

retain water from these peak ﬂow periods for conservation use during low-ﬂow periods (water supply,

low-ﬂow augmentation for environmental protection, irrigation, power production, navigation, recre-

ation, etc.) or to contain peak ﬂows for purposes of reducing downstream ﬂood damage (ﬂood control).

In this section, methods for managing surface-water quantity pursuant to the development of compre-

hensive management alternatives are presented.

The management of a reservoir or system of reservoirs is achieved through a set of operating rules,

that govern releases from the reservoir as a function of such things as inﬂows into the impoundment,

demand for water, storage volumes, and reservoir elevations. Design of the reservoir storage volume, the

spillway, and other reservoir components depends on these rules.

PV FV=+

()

1 i

PV NB

()

APVCR=*

CR =+

()

[]

()

[]

ii i

111

BC PVB PVC=