Wai-Fah Chen.The Civil Engineering Handbook

Подождите немного. Документ загружается.

Theory and Analysis of Structures 47-121

4. Joint: the collapse mode is associated with the rotation of joints of which the adjoining members

developed plastic hinges and deformed under an applied moment, as shown in Fig. 47.100e.

5. Combined: it can be a partial collapse mechanism, as shown in Fig. 47.100f, or it may be a complete

collapse mechanism, as shown in Fig. 47.100g.

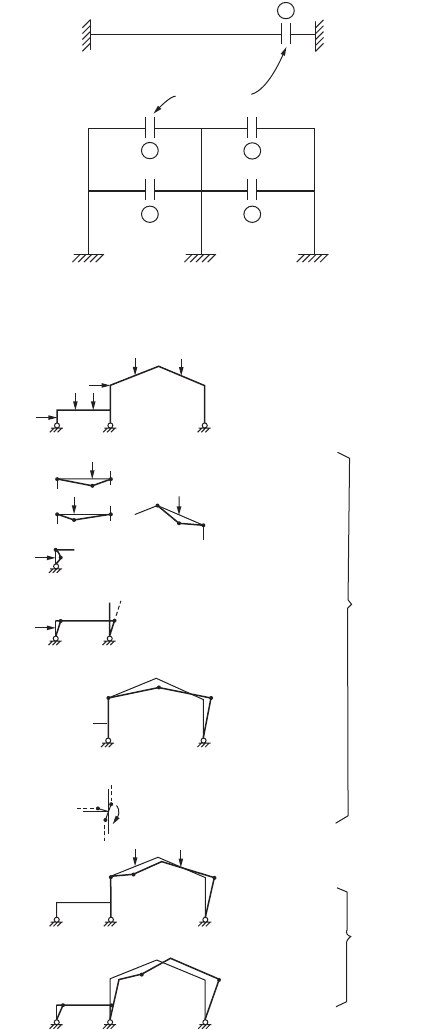
FIGURE 47.99 Number of redundants in: (a) a beam, (b) a frame.

FIGURE 47.100 Typical plastic mechanisms.

3 3

R = 2

R = 12

(a)

(b)

Cut section

(a)

Beam mechanisms

Panel mechanism

Gable mechanism

Joint mechanism

Partial collapse

Complete collapse

Combined

mechanisms

Independent

mechanisms

(b)

(c)

(d)

(e)

(f)

(g)

47-122 The Civil Engineering Handbook, Second Edition

The principal rule for combining independent mechanisms is to obtain a lower value of collapse load.

The combinations are selected in such a way that the external work becomes a maximum and the internal

work becomes a minimum. Thus the work equation would require that the mechanism involve as many

applied loads as possible and at the same time eliminate as many plastic hinges as possible. This procedure

is illustrated in the following example.

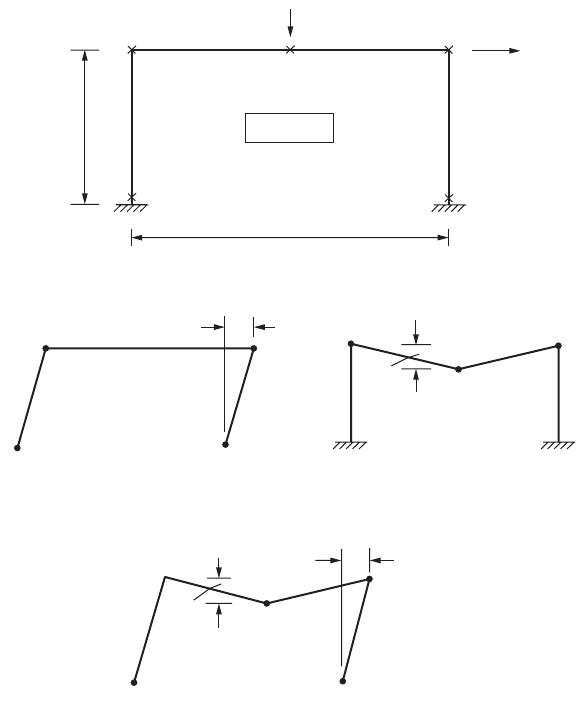
Example 47.13: Rectangular Frame

A ﬁxed-end rectangular frame has a uniform section with M

= 20 and carries the load shown in

Fig. 47.101. Determine the value of load ratio l at collapse.

Solution:

Number of possible plastic hinges: N = 5

Number of redundancies: R = 3

Number of independent mechanisms: N – R = 2

The two independent mechanisms are shown in Fig. 47.101b and c, and the corresponding work equations

are

Panel mechanism: 20l = 4(20) = 80 ﬁ l = 4

Beam mechanism: 30l = 4(20) = 80 ﬁ l = 2.67

FIGURE 47.101 Collapse mechanisms of a ﬁxed base portal frame.

3λ

2λ

(a)

= 20

(b)

10θ

2θ

(c)

(d)

Theory and Analysis of Structures 47-123

The combined mechanisms are now examined to see whether they will produce a lower l value. It is

observed that only one combined mechanism is possible. The mechanism is shown in Fig. 47.101c and

involves cancellation of the plastic hinge at B. The calculation of the limit load is described below:

Panel mechanism: 20l = 4(20)

Beam mechanism: 30l = 4(20)

Addition: 50l = 8(20)

Cancel of plastic hinge: –2(20)

Combined mechanism: 50l = 6(20) ﬁ l = 2.4

The combined mechanism results in a smaller value for l, and no other possible mechanism can produce

a lower load. Thus, l = 2.4 is the collapse load.

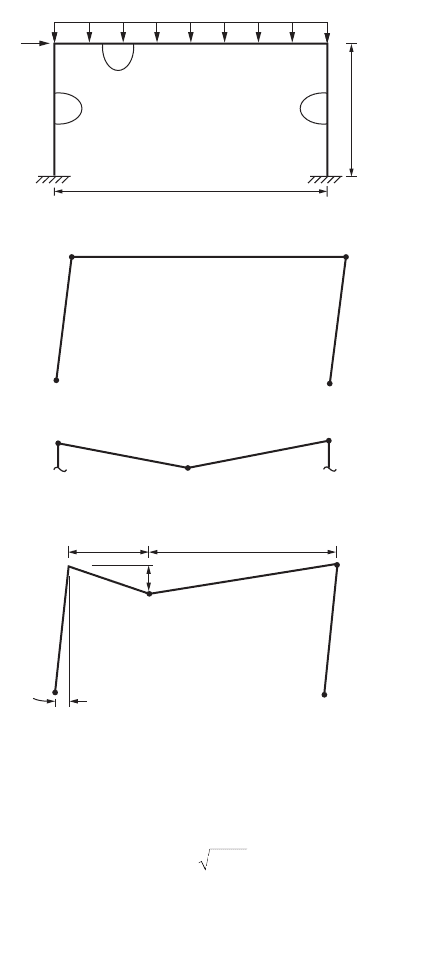
Example 47.14: Frame Subjected to Distributed Load

When a frame is subjected to distributed loads, the maximum moment and hence the plastic hinge

location is not known in advance. The exact location of the plastic hinge may be determined by writing

the work equation in terms of the unknown distance and then maximizing the plastic moment by formal

differentiation.

Consider the frame shown in Fig. 47.102a. The side sway collapse mode in Fig. 47.102b leads to the

following work equation:

which gives

The beam mechanism of Fig. 47.102c gives

which gives

In fact the correct mechanism is shown in Fig. 47.102d, in which the distance Z from the plastic hinge

location is unknown. The work equation is

which gives

To maximize M

, the derivative of M

is set to zero, i.e.,

42410M

()

= 60

10 32M

qq=

()

= 40

24 10

16 20 2 2

qq q

()

()()()

.zM

()

240 16 20

80 2

80 2 80 32 4800 80 16 2 0

()

++-

()

=zz zz

47-124 The Civil Engineering Handbook, Second Edition

which gives

and

In practice, uniform load is often approximated by applying several equivalent point loads to the member

under consideration. Plastic hinges thus can be assumed to form only at the concentrated load points,

and the calculations become simpler when the structural system is getting more complex.

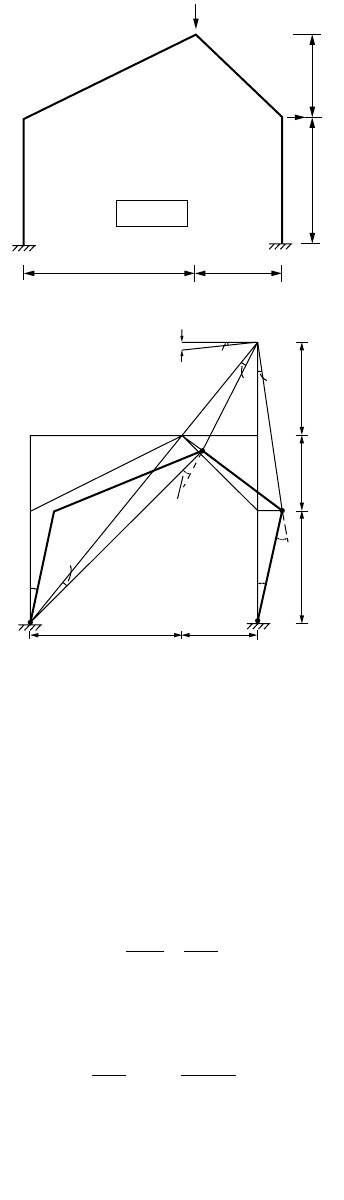
Example 47.15: Gable Frame

The mechanism method is used to determine the plastic limit load of the gable frame shown in Fig. 47.103.

The frame is composed of members with a plastic moment capacity of 270 kip-in. The column bases are

ﬁxed. The frame is loaded by a horizontal load H and vertical concentrated load V. A graph from which

V and H cause the collapse of the frame is to be produced.

FIGURE 47.102 Portal frame subjected to a combined uniform distributed load and horizontal load.

(a)

1.6

(b)

2θ

Zθ

10θ

20θ/(20 − Z)

20 − Z

(c)

(d)

z =- =40 1100 6 83.

= 69 34.

Theory and Analysis of Structures 47-125

Solution:

Consider the three modes of collapse as follows:

Mechanism 1: plastic hinges form at A, C, D, and E:

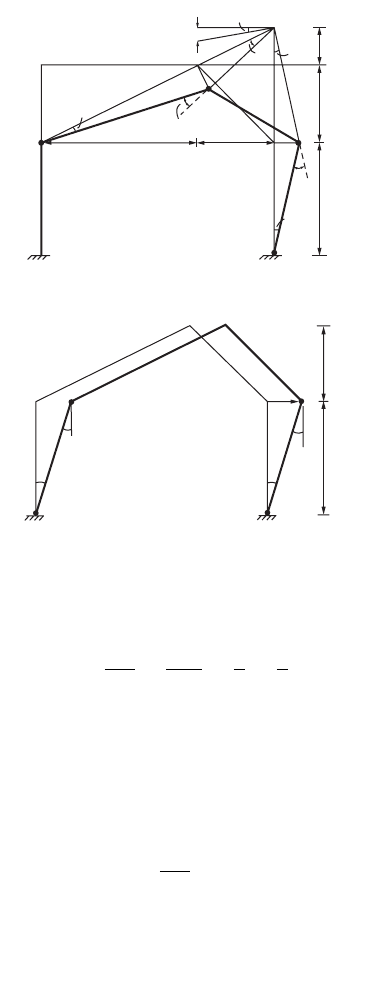
The mechanism is shown in Fig. 47.103b. The instantaneous center O for member CD is located at the

intersection of AC and

D extended. From similar triangles ACC1 and OCC2, we have

which gives

From triangles ACC¢ and CC¢O, we have

FIGURE 47.103 Collapse mechanisms of a ﬁxed base gable frame.

M = 270

(a)

13.5

C′

D′

(f + θ)

(ψ + θ)

9θ

11.25

13.5

(b)

CC ft

22 5 9

11 25==

()

AC OCfq

()

47-126 The Civil Engineering Handbook, Second Edition

which gives

Similarly, from triangles ODD¢ and EDD¢, the rotation at E is given as

which gives

From the hinge rotations and displacements, the work equation for this mechanism can be written as

Substituting values for y and f and simplifying, we have

V + 2.25H = 180

Mechanism 2: mechanism with hinges at B, C, D, and E:

Figure 47.103c shows the mechanism in which the plastic hinge rotations and displacements at the load

points can be expressed in terms of the rotation of member CD about the instantaneous center O.

FIGURE 47.103 (continued).

(f + θ)

(θ + ψ)

9θ

(c)

D′

C′

4.5

13.5

(d)

13.5

13.5θ

fq qqq== ==

DE ODY

()

Y= =

qq15.

VH M

9135qffqq

()

=++

()

[]

. YYY

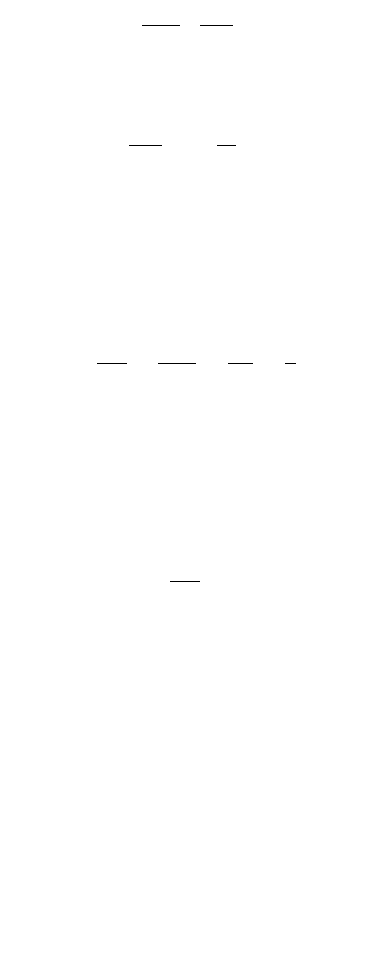
Theory and Analysis of Structures 47-127

From similar triangles BCC

and OCC

, we have

which gives

From triangles BCC¢ and CC¢O, we have

which gives

Similarly, from triangles ODD¢ and EDD¢, the rotation at E is given as

which gives

The work equation for this mechanism can be written as

Substituting values of y and f and simplifying, we have

V + 1.5H = 150

Mechanism 3: mechanism with hinges at A, B, D, and E:

The hinge rotations and displacements corresponding to this mechanism are shown in Fig. 47.103d. The

rotation of all hinges is q. The horizontal load moves by 13.5q, but the horizontal load has no vertical

displacement. The work equation becomes

H = 80

The interaction equations corresponding to the three mechanisms are plotted in Fig. 47.104. By carrying

out moment checks, it can be shown that mechanism 1 is valid for portion AB of the curve, mechanism

2 is valid for portion BC, and mechanism 3 is valid only when V = 0.

945==

()

= .

BC OCfq

()

fq qqq== ==

DE ODY

()

Y= =

VH M

9135qffqq

()

=++

()

[]

. YYY

13 5. q qqqq

()

= +++

()

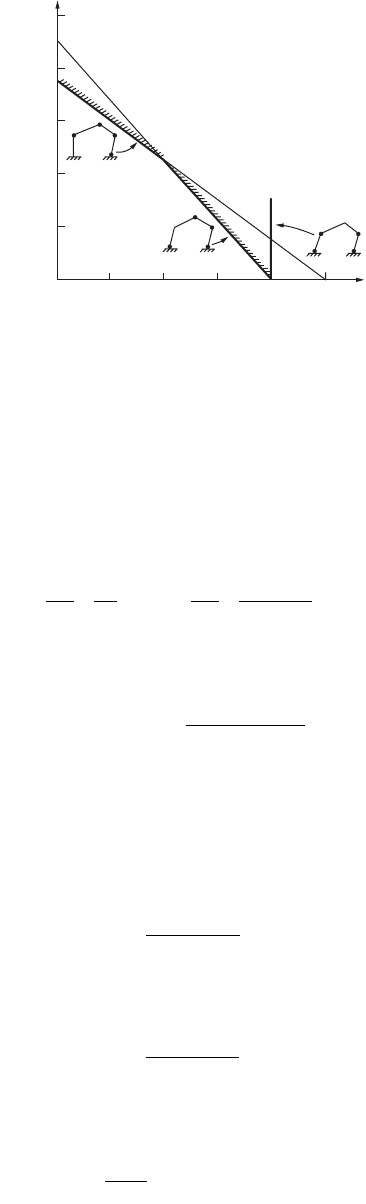
47-128 The Civil Engineering Handbook, Second Edition

Analysis Aids for Gable Frames

Pin-Based Gable Frames

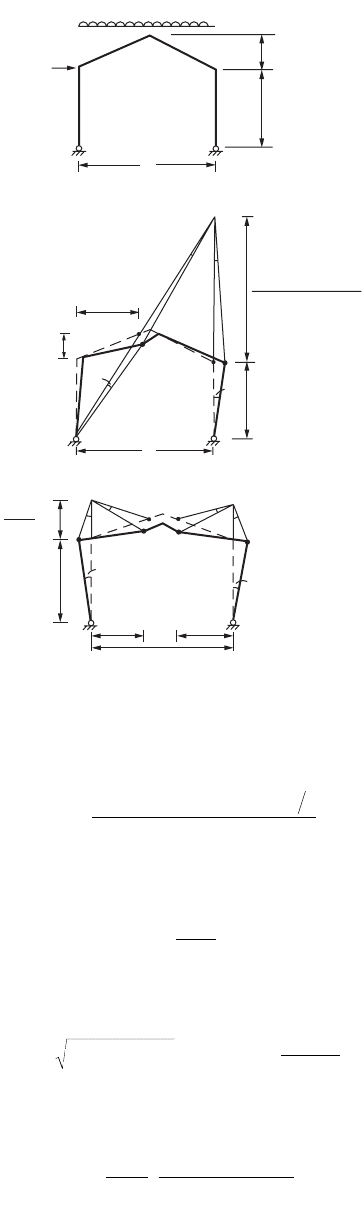
Figure 47.105a shows a pinned-end gable frame subjected to a uniform gravity load lwL and a horizontal

load l1H at the column top. The collapse mechanism is shown in Fig. 47.105b. The work equation is

used to determine the plastic limit load. First, the instantaneous center of rotation O is determined by

considering similar triangles,

(47.227)

and

(47.228)

From the horizontal displacement of D,

(47.229)

of which

(47.230)

where k = h

. From the vertical displacement at C,

(47.231)

The work equation for the assumed mechanism is

(47.232)

FIGURE 47.104 Vertical load and horizontal force interaction curve for collapse analysis of gable frame.

200

160

120

(2)

V + 1.5H = 150

V + 2.25H = 180

(1)

(3)

H = 80

100

20 40 60 80

and

hxh

OD OE h

xh xh

=-=

()

qfhOD

fq=

()

xxk12

bq=

()

xxk

fbfq

12Hh

()

=++

()

Theory and Analysis of Structures 47-129

which gives

(47.233)

Differentiating M

in Eq. (47.233) with respect to x and solving for x,

(47.234)

where

(47.235)

Substituting for x in the expression for M

gives

(47.236)

FIGURE 47.105 Pinned base gable frame subjected to a combined uniform distributed load and horizontal load.

(a)

= kh

λwL

1 − x

xL xL

(c)

2xh

(b)

(1 − x)h

+ 2xh

xHh xxwL

()

112

-1

AkUkand U

()

=11

AAUk

()

+- +

47-130 The Civil Engineering Handbook, Second Edition

In the absence of horizontal loading, the gable mechanism, as shown in Fig. 47.105c, is the failure mode.

In this case, letting H = 0 and U = 0 gives (Horne, 1964):

(47.237)

Equation (47.236) can be used to produce a chart, as shown in Fig. 47.106, by which the value of M

can be determined rapidly by knowing the values of

(47.238)

Fixed-Base Gable Frames

A similar chart can be generated for ﬁxed-base gable frames, as shown in Fig. 47.107. Thus, if the values

of loading, lw and l

H, and frame geometry, h

, h

, and L, are known, the parameters k and U can be

evaluated and the corresponding value of M

/(lwL

) can be read directly from the appropriate chart.

The required value of M

is obtained by multiplying the value of M

/(lwL

) by lwL

Grillages

Grillage is a type of structure that consists of straight beams lying on the same plane, subjected to loads

acting perpendicular to the plane. An example of such a structure is shown in Fig. 47.108. The grillage

consists of two equal simply supported beams of span length 2L and full plastic moment M

. The two

beams are connected rigidly at their centers, where a concentrated load W is carried.

The collapse mechanism consists of four plastic hinges formed at the beams adjacent to the point load,

as shown in Fig. 47.108. The work equation is

FIGURE 47.106 Analysis chart for pinned base gable frame.

0.6

Sway mechanism

0.16

0.14

0.12

0.10

0.08

0.06

0.04

0.02

λωL

U =

2λ

λωL

k = 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

Gable mechanism

0.5

0.4

0.3

0.2

0.1

U=0

++ +

and U

WL M

qq= 4