Weingast B.R., Wittman D. The Oxford Handbook of Political Economy

Подождите немного. Документ загружается.

392 a tool kit for voting theory

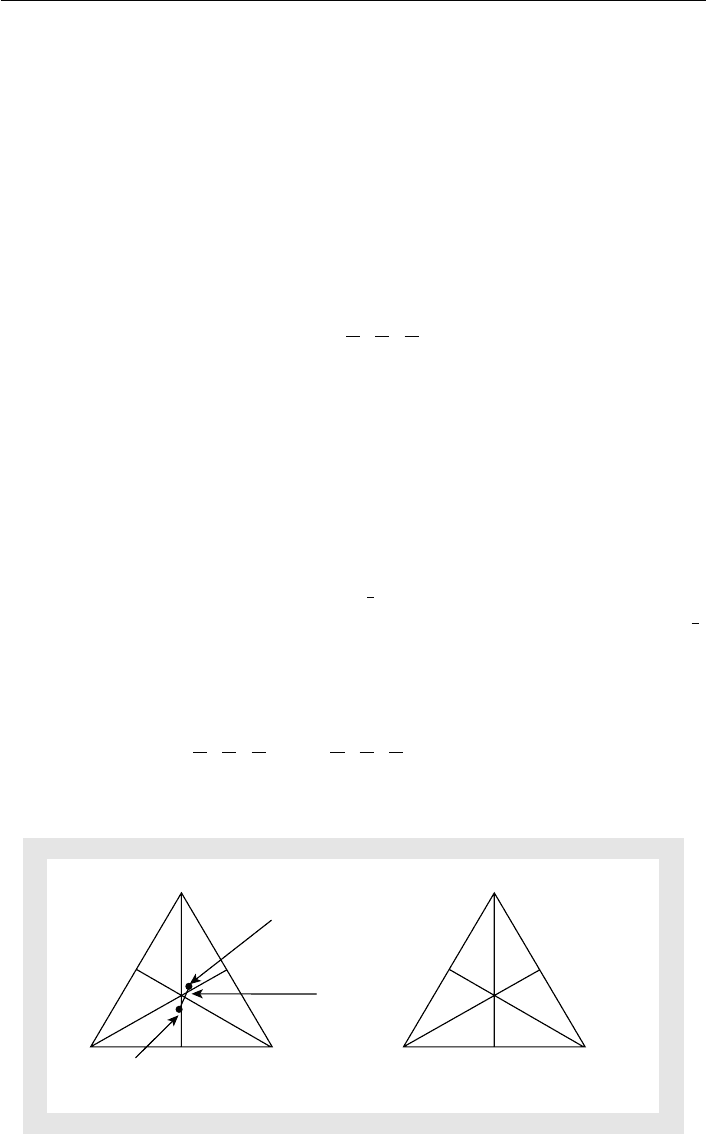
Figure 22.1a represent:

Label Ranking

Label Ranking Label Ranking

1 A  B  C 2 A  C  B 3 C  A  B

4 C  B  A

5 B  C  A 6 B  A  C

(1)

To represent a proﬁle for {Ann, Barb, Connie}:

Number Ranking

Number Ranking Number Ranking

6 A  B  C 0 A  C  B 6 C  A  B

3 C  B  A

2 B  C  A 6 B  A  C

(2)

to elect a departmental chair, place the number of voters with each ranking in the

appropriate ranking region: this equation 2 “Chair”proﬁleisinFigure22.1b.

As described in Saari (2001), the geometric representation sorts proﬁle entries in

a manner that simpliﬁes tallying elections; e.g. as all voters preferring A  B are to

theleftoftheverticalline,theirsum6+0+6=12isA’s tally in the {A, B} election.

This number, with B’s 3 + 2 + 6 = 11 tally from the right of the line, is listed under the

edge. All pairwise outcomes are similarly computed with the outcomes listed near the

appropriate triangle edge. According to these votes, Ann is the Condorcet winner—she

beats all others in pairwise majority votes.

Our standard voting system, where a voter votes for his favorite candidate and the

candidate with the most votes wins, is called the plurality vote. But rather than voting

just for one candidate, we might give 9, 7, 0 points, respectively, to a voter’s top-,

second-, and third-ranked candidate. This is called a “positional election:” it is where

the weights w

≥ w

= 0 are assigned, respectively, to a voter’s top, second, and

bottom “positioned” (ranked) candidates and the societal ranking is determined by

the sum of points each candidate receives. Without loss of generality, scale all weights

by dividing by w

to obtain (1, s, 0). So with the earlier 9, 7, 0 points assignment,

the rescaling assigns 1, s =

, 0 points to a voter’s top-, second-, and third-ranked

candidate. To use weights that play a major role in what follows, the Borda Count is

where 2, 1, 0 points are assigned to the candidates, so its scaled weights are (1,

, 0).

The antiplurality vote, 1, 1, 0 (called this because by voting for two, you are eﬀectively

voting against someone), already is in scaled form.

To compute tallies, notice that Ann’s outcome is [number of voters with A

top-ranked]+ s [number of voters with A second ranked]. In Figure 22.1b,theﬁrst

bracket’s value is A’s plurality outcome, or the sum of numbers in regions with A as a

vertex: 6 + 0 = 6. The second bracket—the number of voters with A second ranked—

involves the two triangles one step removed from where A is top ranked—the adjacent

regions that both contain 6.ThusA’s positional tally is [6 + 0] + s [6 + 6] = 6 + 12s.

All positional tallies are similarly computed and listed by the appropriate Figure 22.1b

vertex. Readers unfamiliar with this process should experiment by computing elec-

tion outcomes for other proﬁles.

According to Figure 22.1b the plurality (s =0)rankingisC  B  A with a 9 : 8 : 6

tally, so Connie, rather than Condorcet winner Ann, wins. But as the antiplurality sys-

tem (s =1)hastheoppositeoutcomeofA  B  C with a 18 : 17 : 11 tally, Condorcet

donald g. saari 393

winner Ann wins with some of the positional methods. Later I show the reader how

to construct this Chair proﬁle and many others.

3 Procedure Line and Hulls

.............................................................................

The above approach simpliﬁes computing tallies but it does not display the diﬀerent

outcomes. The next geometric approach that I developed (Saari 1994, which has been

used by Nurmi 2003, Tabarrok 2001, Tabarrok and Spector 1999 to analyze elections)

rectiﬁes this deﬁciency. To explain, re-express the (6, 8, 9) plurality outcome (in the

A, B, C order) of the Chair example as (

) describing each candidate’s frac-

tion of the vote: call this the normalized election tally.Asx, y, z represent, respectively,

the fraction of the vote received by Ann, Barb, and Connie, we have:

x, y, z ≥ 0, x + y + z =1. (3)

When the points in equation 3 are graphed on an x, y, z coordinate system, the

region connects the point on each positive axis that is one unit from the origin. As

a quick drawing will prove, the ﬁgure is an equilateral triangle (Figure 22.2a): points

in this triangle identify normalized tallies. For instance, the A-vertex corresponds to

x =1whereA receives all of the vote. The triangle’s midpoint, where all lines cross,

represents a complete tie with x = y = z =

, which means that each candidate re-

ceives a third of the vote. The midpoint on the right-side leg, where x =0, y = z =

represents a B ∼ C  A election outcome.

Procedure line. To ﬁnd all possible positional election outcomes for a proﬁle, plot

the normalized plurality and antiplurality outcomes and connect them with a straight

line (Saari 1994). To illustrate, the normalized plurality and antiplurality outcomes

of the Chair election (

)and(

) are plotted in Figure 22.2a.(Inan

equilateral triangle with leg length 2 where (u,v) represents the coordinates, the

(1, 0, 0), (0, 1, 0), (0, 0, 1) unanimity election outcomes are plotted in the ﬁgure as

2 + 6s

3 + 0s

3 + 2s

Plurality

Antiplurality

(a) Procedure line (b) Computing a profile

Procedure line

Fig. 22.2 Procedure lines

394 a tool kit for voting theory

the (u,v)points(0, 0), (2, 0), (1,

√

3). In general, plot the election point (x, y, z)

according to:

u =2y + z,v=

√

3z;

e.g. the Chair plurality point is at u =2≈

≈ 1.0870, while v =

√

3 ≈ 0.6777.) The importance of the line connecting the plurality and antiplurality

points, the procedure line, is that each point represents some positional procedure’s

normalized election tally, and all positional outcomes are represented on this line. To

explain, notice that the values listed by the vertices in Figure 22.1b,whichspecifyall

possible positional outcomes, deﬁne a linear equation (i.e. the exponent on s is one).

Thus the set of outcomes deﬁne a line: this is the procedure line.

All sorts of information comes from the positioning of this procedure line; e.g. in

Figure 22.2a, each candidate from the Chair election can “win” with an appropriate

positional method. As examples, Ann wins with the antiplurality method (s =1),

Barb with the earlier deﬁned Borda Count (s =

), and Connie with the plurality vote

(s = 0). This ambiguity raises an issue: who is the true “choice of the voters?” The fact

the procedure line crosses seven regions (three are line segments and four are open

triangles) means that this proﬁle deﬁnes the seven diﬀerent positional election rankings:

C  B  A, C ∼ B  A, B  C  A, B  A ∼ C,

B  A  C, A ∼ B  C, A  B  C.

Most of the procedure line is in regions where Barb wins, which means that most

positional methods elect B; e.g. we can argue that B is the appropriate choice.

Beyond cataloguing all positional outcomes allowed by a proﬁle, Tabarrok (2001;

Tabarrok and Spector 1999) uses the procedure line and hull (that is needed with

more than three candidates: Saari 2001a) to extract comparisons about elections and

the “true winner.”

Creating proﬁles and proﬁle lines. Can we construct proﬁles to illustrate particular

behaviors; e.g. is there a proﬁle with the plurality A ∼ C  B and antiplurality

B  C  A outcomes? If so, what happens with the other positional outcomes? To

answer such questions, place two points in the triangle for the desired plurality and

antiplurality outcomes, and connect them to deﬁne the procedure line. The points

must satisfy the following:

1.Plurality(x, y, z) can be any desired point with non-negative fractional compo-

nents that satisfy x + y + z =1.

. Antiplurality point (X, Y, Z) with non-negative fractional components must

satisfy:

(a)0≤ X, Y, Z ≤

, X + Y + Z =1.

(b) X ≥

, Y ≥

, Z ≥

example.

To illustrate, I will create an example where the A ∼ C  B plurality outcome

is accompanied by the antiplurality B  C  A.Let(x, y, z)=(

)deﬁnethe

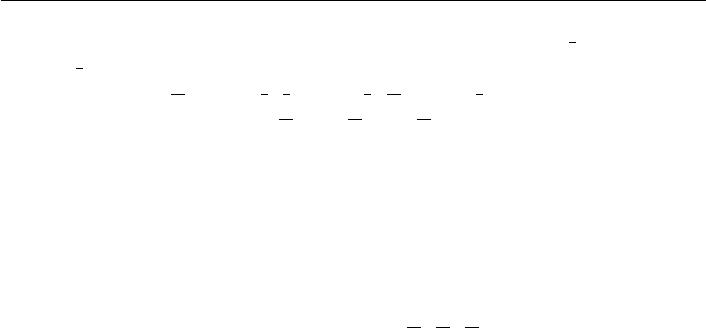
donald g. saari 395

desired A ∼ C  B plurality ranking. (So, A and C each receive

of the vote, B

receives

.) These normalized plurality tallies require the normalized antiplural-

ity tallies to satisfy

≤ X ≤

≤ Y ≤

≤ Z ≤

.TohavetheB  C  A

antiplurality outcome, let X =

, Z =

, Y =

. By plotting the (x, y, z)and

(X, Y, Z) point to create the procedure line, it follows that any supporting proﬁle

allows the six election rankings A ∼ C  B, C  A  B, C  A ∼ B, C  B  A,

C ∼ B  A, B  C  A.

To construct a supporting proﬁle, convert (x, y, z)and(X, Y, Z)tointegervalues

where the integer antiplurality outcomes sum to twice the plurality outcomes. (This

is because with the plurality and antiplurality votes, each voter casts, respectively, one

and two points.) With our example, multiply the plurality outcome by its common

denominator of eight to get (3, 2, 3), and the (

) outcome by its common

denominator of 16 to obtain the desired (3, 8, 5). (This approach always works if

the common denominator for the normalized antiplurality tally is twice that of the

normalized plurality tally.)

Now notice from Figure 22.1b that the s -coeﬃcient for each candidate is the dif-

ference between her plurality and antiplurality tallies. So a proﬁle satisfying our

example deﬁnes the A, B,andC positional outcomes of 3 + s (3 −3), 2+s (8 − 2),

and 3 + s (5 −3). These values are listed next to the appropriate Figure 22.2b vertex.

Compute the a through f integervaluesinFigure22.2b as above; e.g. Ann’s tally

of 3 + 0s =[a + b]+s[ f + c]. Ann has no “second-place votes,” so c = f =0. As

Barb’s plurality vote is 2 = (e + f )and f =0,wehavethate = 2. Similarly, d =3.

It remains to divide Ann’s a + b = 3 ﬁrst-place votes to satisfy the s -coeﬃcients for

Barb and Connie: the only choice is a = 3. Thus, the eight-voter supporting proﬁle

for the example has three voters preferring A 

B  C, two preferring B  C  A,

and three preferring C  B  A.

The missing technical condition is that a candidate’s s-coeﬃcient cannot exceed

the sum of the other two candidates’ plurality votes; e.g. as the s-coeﬃcient comes

from the other candidates’ ﬁrst-place votes, there must be enough of them.

This approach makes it easy to construct proﬁles to exhibit all sorts of interesting

behavior. In practical terms, just draw a line in the triangle. Almost any line suﬃces:

if the endpoints are close to the center, the above conditions will be satisﬁed. Often

just the positioning of the procedure line suﬃces to discover conclusions; e.g. in this

manner we now know the following. I leave the proofs to the reader; they just involve

drawinganappropriatelineinanequilateraltriangle:

For any ranking, there is a proﬁle where all normalized positional outcomes agree

and yield the selected ranking. (Select the normalized plurality and antiplurality

points to be the same; the procedure line becomes a point where all normalized

tallies agree.)

Select any ranking for the plurality and for the antiplurality outcomes. There

exists a proﬁle with these outcomes. In fact, select any two diﬀerent positional

methods and any two ranking: there exists a proﬁle so that the ﬁrst rule’s

outcome is the ﬁrst ranking while the second rule’s outcome is the second

ranking.

396 a tool kit for voting theory

For any number from {1, 2,...,7}, there exists a proﬁle with precisely that

number of diﬀerent positional outcomes.

Approval voting. To show how to compute outcomes for other rules, I illustrate

the approach with approval voting (AV). AV, analyzed and promoted by Brams and

Fishburn (1983), is where a voter votes “approval” for as many candidates as desired.

So a voter with A  B  C preferences could vote for Ann, or for Ann and Barbara.

While a vote for all three is admissible, Brams and Fishburn cogently argue that such

a vote is not rational because, by not distinguishing among the candidates, the voter’s

ballot has no eﬀect.

Obviously, if voters vote in diﬀerent ways, the AV outcome can change. Indeed,

Ann from the Chair election could receive thirteen diﬀerent AV election tallies ranging

from 6 to 18 votes! A quick way to determine all values a candidate can receive is to

recognize that the range is deﬁned by her plurality (vote for one) and antiplurality

(vote for two) tallies. As there are 13 diﬀerent AV tallies for Ann, 10 for Barb, and 3 for

Connie, the Chair proﬁle admits 13 × 10 ×3 = 390 diﬀerent AV election tallies! (It

is easy to create scenarios that support each outcome.)

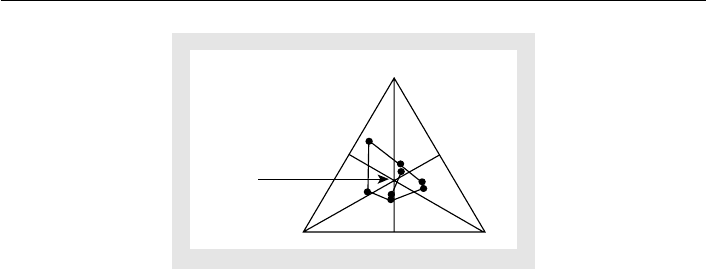
Plotting 390 points is not appealing, so to identify all AV outcomes plot the eight

extreme tallies constructed from the plurality (6, 8, 9) and antiplurality (18, 17, 11)

by interchanging values from each list. This selection represents where a candidate

receives only ﬁrst-place votes (plurality tally) or all possible second-place votes (an-

tiplurality tally). As the eight extreme tallies are:

(6, 8, 9) (18, 8, 9) (6, 17, 9) (6, 8, 11)

(18, 17, 11) (6, 17, 11) (18, 8, 11) (18,

17, 9),

(4)

plot (Figure 22.3) the eight normalized tallies:













(5)

Connect all points with straight lines: the enclosed region contains all 390 tallies

that are (essentially) equally spaced in this region. While “only” 390 points in this

Figure 22.3 AV hull are AV election tallies, because they are closely packed into a small

region, it is reasonable to view all points in this distorted rectangle as admissible AV

tallies.

The Figure 22.3 graph identiﬁes several conclusions: a partial sample follows. (For

more AV properties, see Saari 1994, 2001a; Saari and van Newenhizen 1988.)

1. If the reader ﬁnds it disturbing that the Chair proﬁle allows seven diﬀerent

positional outcomes, the reader will be more disturbed by Figure 22.3 showing

that any ranking can be a sincere AV outcome for this proﬁle! This is because

the AV hull meets all six short-line segments (representing a tie between candi-

dates), the center point (complete tie), and all six open regions (strict election

outcomes). This indeterminate phenomenon is not a peculiarity of the Chair

election example: multiple outcomes are to be expected. Indeed, even an una-

nimity proﬁle allows diﬀerent election rankings.

donald g. saari 397

Procedure line

Fig. 22.3 Approval Voting hull

2. For any proﬁle, every positional election ranking is a sincere AV election out-

come. This is because two of the plotted points are the procedure line’s end-

points. Consequently, for any proﬁle, the procedure line always is in the AV hull.

3.AsFigure22.3 demonstrates, most points in the AV hull (e.g. most AV tallies)

elect the Condorcet loser Connie! This geometry, then, shows how easy it is for

AV to elect the Condorcet loser.

With so many AV outcomes, we must wonder which ones are likely to occur.

Valued help in answering this question comes from extending Brams and Fishburn’s

commentary that a voter must distinguish among candidates, rather than voting for

all, to avoid losing any say in who is elected. Similarly, in an election closely con-

tested between a voter’s two top choices, the rational voter should vote for only one

candidate: otherwise the voter has no say in which candidate is elected. To illustrate

with the 1992 US presidential elections, voters preferring “Clinton  Bush  Perot,”

or “Bush  Clinton  Perot” would vote only for their top-ranked candidate: by

voting for two, their vote would not inﬂuence the Clinton–Bush outcome and, from

a pragmatic perspective, it would be equivalent to not voting. Similarly, because the

Perot voters wanted their candidate to come close to one of the major candidates, they

probably would vote only for Perot. Thus the only voters with any rational motivation

to vote for two candidates are those with Perot second ranked. If enough did so,

we would have had President Perot. (See Tabarrok 2001 for supporting data.) An

unfortunate but natural consequence is that in closely contested elections, AV reduces

to the plurality vote—the procedure it was designed to replace—or worse.

4 Dictionaries,Paradoxes,

and Properties

.............................................................................

In selecting election rules, we should be guided by their properties. This suggests

using the “axiomatic representations” of voting rules. After all, as papers using this

method occasionally argue, this approach tells us “what we are getting.”

398 a tool kit for voting theory

This approach sounds too good to be true, and that is the case. My cautionary

advice is to avoid putting too much trust in these conclusions as they can be seriously

misleading. The reason is that many “axiomatic” studies in the social sciences have

little, if anything, to do with axiomatics. Rather than “axioms,” they are using what

we mathematicians call “properties” or “hypotheses.” In blunt terms, most of these

conclusions only show which particular properties happen to identify uniquely a

particular decision rule. But “uniquely identifying” and “characterizing” are very

diﬀerent traits: in particular, most results from this approach fail to characterize what

yougetfromadecisionrule.

To illustrate with a non-technical illustration, consider the three traits (1) Finnish-

American heritage, (2) born in a particular year in the Upper Peninsula of Michigan,

and (3) does research in social choice and the Newtonian N-body problem. While

these traits uniquely identify me, they do not characterize me. Knowing just this,

you do not know “what you are getting.” Similarly the traditional “axiomatic studies”

often identify properties that, by emphasizing special settings, uniquely identify an

election rule. But unless these properties can be used to derive all properties of the

rule, then instead of being “axioms,” they are just special properties the rule happens

to satisfy.

If the axiomatic approach does not accomplish what we want, how do we ﬁnd

all properties of a voting rule? In addressing this question, I was inﬂuenced by the

research of Nurmi, Brams, and Fishburn. In particular, Fishburn (1981) published

an intriguing paradox (that is, a counterintuitive outcome) where the sincere plu-

rality election outcome is A  B  C  D,butifD drops out, the sincere election

outcome for the same voters—nobody changes preferences!—becomes the reversed

C  B  A. Fishburn’s reversal example is more than an amusing curiosity: it illus-

trates a peculiar and unexpected property of the plurality vote.

The ranking “paradoxes” in the literature must be taken seriously because they

identify properties of election rules. Similarly, “paradoxes that cannot occur” identify

a rule’s positive properties. To illustrate with the Borda Count (where 2, 1, 0 points

are assigned, respectively, to a voter’s top-, second-, and bottom-ranked candidate),

this rule does not allow the list

(B  C  A, A  B, A  C, B  C)

to ever happen. This and other lists of Borda rankings that cannot occur deﬁne

the important property that the Borda Count never ranks the Condorcet loser (the

candidate that loses to all candidates in pairwise elections) above the Condorcet

winner. Does this property extend to any other positional method? (No.)

To ﬁnd all ranking properties of election procedures, we could ﬁnd all possible

lists of election rankings that could ever occur. To illustrate with Fishburn’s example,

rather than just the plurality (A  B  C  D, C  B  A)listing,wewantto

know what happens with all subsets of candidates. Can we have, for instance, a

plurality listing

(A  B  C  D, C

 B  A, D  B  A, D  C  A, D  C  B,

A  B, B  C, C  D, D  A, A  C, B  D)

donald g. saari 399

where the plurality ranking reverses if any candidate is dropped, but the pairwise

outcomes are cyclic? As there are many proﬁles with precisely this property, this listing

deﬁnes another property of the plurality vote.

By modifying notions from “chaotic dynamics” (the intrepid reader can check

Saari 1995), I was able to ﬁnd everything that could ever happen for any num-

ber of candidates, any number of voters, and all combinations of positional voting

methods (Saari 1989, 1990). To explain the discouraging results with, say, candidates

{A, B, C, D, E }, rank them in any desired manner; e.g. A  B ∼ C  D ∼ E .For

each way to drop a candidate, rerank the remaining four in any desired manner; e.g.

dropping E , select D  C  B  A,droppingD choose E  A  B ∼ C ...Next,

dropping two candidates creates ten three-candidate subsets: rank each in any desired

manner. Finally, rank each pair in any desired manner. For any listing designed in

this almost random fashion, there is a proﬁle so that for each subset of candidates,

the sincere plurality election outcome is the selected ranking. This conclusion, which

holds for any number of candidates, is a discouraging commentary on our standard

election method: it means that with the plurality vote “anything can happen.”

Beyond the plurality vote, select a positional method for each subset of candidates;

e.g. maybe the “vote for three” scheme for ﬁve-candidate sets, “vote for two” for

four-candidate subsets, and a (7, 6, 0) method for all triplets. The same assertion

holds: for almost all choices of positional methods, anything can happen. This “almost

all” modiﬁer provides hope by suggesting that by carefully selecting voting methods,

we might provide consistency among election outcomes. This is the case. It turns

out that there are certain special combinations of positional methods that prohibit

some ranking lists from ever occurring, so they impose some consistency among

the election rankings as candidates are added or dropped. But the choices can be

complicated. As an illustration, if four candidate elections are tallied by assigning

3, 1, 0, 0 points, respectively, to a top-, second-, third-, and bottom-ranked candidate,

then the four-candidate outcome never bottom-ranks a candidate who wins all three-

candidate plurality contests. Rather than describing these complicated results, let me

cut to the chase by identifying the unique method with the ultimate consistency.

With n-candidates, the Borda Count assigns a candidate the same number of points

as there are lower-ranked candidates on the ballot. So for ﬁve candidates, the Borda

Count assigns 4, 3, 2, 1, 0 points, respectively, to a top-, second-, third-, fourth-, and

bottom-ranked candidate. A main result is that the maximum consistency in election

rankings is attained only by using the Borda Count with all subsets of candidates. More

precisely, any ranking list coming from the Borda Count also arises with any other

combination of voting rules! But if a non-Borda method is assigned to any subset of

candidates, the system generates ranking outcomes that never occur with the Borda

method. Moreover, the diﬀerences in kinds and numbers of unexpected election

outcomes (paradoxes) are mind boggling. To illustrate with seven candidates, it would

be impressive if, for instance, the number of plurality ranking lists is three times that

of the Borda Count: this multiple would measure the increased inconsistency of the

plurality vote. This assertion, however, is far too modest: the plurality vote generates

more than 10

more lists than the Borda Count! This number, a 1 followed by ﬁfty

400 a tool kit for voting theory

zeros, is so large that even if a million of the world’s fastest computers started counting

at the “Big Bang” they would not be even 1 per cent of the way to this number. The

situation becomes worse with eight candidates.

Only the Borda Count provides maximal consistency among election rankings and

avoids, by far, the most “paradoxes.” To develop some intuition about the source of

the Borda Count consistency, consider a voter with preferences A  B  C.Inthe

three pairwise elections, this voter votes as follows:

Pair ABC

{A, B} 10—

{A, C}

1—0

{B, C}

—1 0

Tot al 210

(6)

The bottom “Total” line agrees with the number of points assigned by the Borda

Count to candidates for this A  B  C ranking. (This phenomenon holds for any

number of candidates.) In other words, the Borda Count is the natural extension

of the pairwise vote because its tally for any candidate equals the sum of votes the

candidate would have received in all pairwise comparisons.

5 The “Will of the Voters”

.............................................................................

A basic problem remains: how do we determine the “will of the voters?” Maybe,

for instance, a “paradox” avoided by the Borda Count best reﬂects what the voters

want. But to know what the voters want, we must concentrate on what they say

they want—we must examine the information coming from the proﬁles. Although

obvious, I did not entertain this approach until I recognized that our traditional

approach of ﬁnding properties of voting rules failed to provide the desired insight.

The reason for this failing is that the traditional approach emphasizes partially

processed information about the voter preferences rather than preferences. Also,

there are too many properties to allow a careful study; e.g. it is impossible in any

number of lifetimes to examine the 10

ways the plurality vote diﬀers from each list of

Borda rankings.

A full description of how to analyze preferences to determine the “will of the

voters” is in Saari (1999, 2000, 2001a), so only basic notions are described here. The

idea is to ﬁnd “conﬁgurations of preferences” where it is arguable that the outcome

should be a complete tie: if a voting rule does not deliver a complete tie, then it may

introduce a bias favoring certain candidates. I conjectured that all possible voting

diﬀerences (for positional, pairwise, and methods based on them) could be explained

in this manner. This conjecture turned out to be correct. I indicate what happens for

three candidates. (The result holds for any number of candidates (Saari 2000), but a

more readable book version is being prepared.)

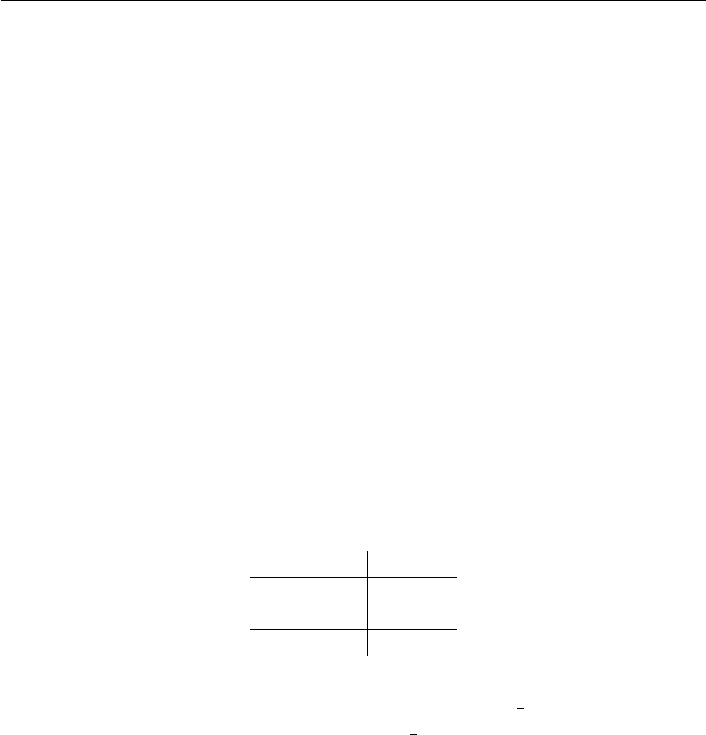
donald g. saari 401

In selecting these conﬁgurations, certain properties must be observed.

1. The conﬁguration must make it arguable that the outcome should be a complete

tie.

2. While the outcomes of certain decision rules should be a complete tie, others

should not be tied so that we can distinguish among voting rules.

3. Enough conﬁguration of preferences should be found so that all proﬁles can

be analyzed. (But no other conﬁgurations as this would become redundant

information.)

Surprisingly, for three candidates, only two diﬀerent conﬁgurations of preferences

are needed to analyze all possible three-candidate election outcomes. After describing

both conﬁgurations, I use them to derive some examples and explain some theoretical

results in the literature. Details and supporting arguments are left to the references

Saari (1999, 2000, 2001a).

Neutral reversal requirement (NRR). Imagine the advantages if your spouse’s polit-

ical views are completely opposite of yours: on a sunny day neither of you needs to

vote as your votes would cancel. This is NRR. For example, with the two-voter proﬁle

(A  B  C, C  B  A), the pairwise majority votes always are tied: a pairwise

ranking in A  B  C is reversed in C  B  A. But with positional methods

captured by (1, s, 0), we have the tally:

Ranking

ABC

A  B  C 1 s 0

C  B  A

0 s 1

Tot al 12s 1

(7)

So, a complete tie vote occurs if and only if 2s = 1, or with the Borda Count.

All other positional methods introduce a bias; e.g. using s <

causes a A ∼ C  B

outcome biased against B. Conversely, using s >

causes B  A ∼ C biased in favor

of B. The surprising fact (Saari 1999, 2001a)isthatall possible diﬀerences among three-

candidate positional election outcomes are caused by these NRR reversal components!

Below I use this fact to create proﬁles.

Neutral Condorcet requirement (NCR). The next set of three-candidate require-

ments is based on the Condorcet triplet. The two sets are

A  B  C, B  C  A, C  A  B

and

A  C  B, C  B  A, B  A  C

where a top-ranked candidate is dropped to bottom place in the next ranking. Because

each candidate is in ﬁrst, second, and third place with a Condorcet triplet, it is

reasonable to argue that the outcome should be a complete tie: it is for positional

outcomes where each candidate’s tally is w

+ w

or 1 + s.

The pairwise majority vote refuses to honor NCR by delivering the A  B, B  C,

C  A cycle for the ﬁrst Condorcet triplet: each outcome has a 2 : 1 vote. The reason