Weingast B.R., Wittman D. The Oxford Handbook of Political Economy

Подождите немного. Документ загружается.

402 a tool kit for voting theory

3 + x

y + z

1 + 2x

1 + y + (2 + 2z)s

1 + y 2 + z

2 + z + (1+ 2y)s

2 + x

3 + 2x

1 + x

(a) NCR and pairwise votes (b) NRR and positional outcomes

Fig. 22.4 Constructing examples

for this bias is that by myopically concentrating on how a pair fares in each ranking,

the pairwise vote misses the broader symmetry supporting a complete tie. Surpris-

ingly (Saari 1999, 2001a), all possible diﬀerences between the Borda Count and pairwise

outcomes, and all possible diﬀerences among methods based on pairwise outcomes, are

caused by proﬁle components given by the Condorcet triplets.

Constructing examples. Surprisingly, the two-century-old topic of comparing vot-

ing procedures reduces to the simple observation whether a proﬁle has components

in the NRR and NCR directions. Readers interested in exploring this approach

for three candidates should check Saari (1999, 2001a); see Saari (2000) for n ≥ 3

candidates. To illustrate, I show how to construct examples that do anything that

can arise.

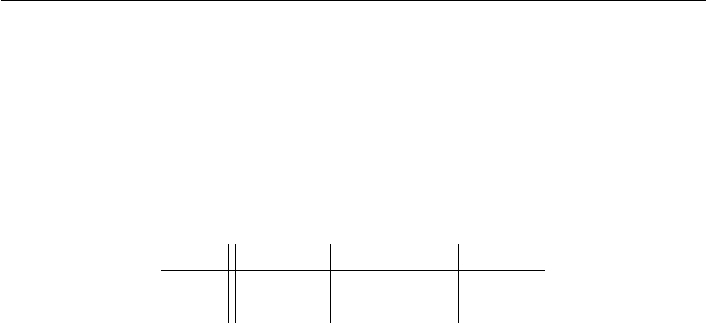
Start with the proﬁle where one voter prefers A  B  C and two prefer

B  A  C. This proﬁle has the positional outcomes A, B, C of, respectively,

1+2s, 2+s, 0. Thus for s < 1, the outcome is B  A  C. The pairwise votes are

compatible with B  A, B  C, A  C outcomes that crown Barb as the Condorcet

winner. With this proﬁle, most standard methods agree giving the same B  A  C

outcome.

To distort this proﬁle to create the Chair proﬁle, ﬁrst change the Condorcet winner

from B to A without aﬀecting any positional ranking. According to NCR, this requ-

ires adding x units of the Condorcet triplet, A  B  C,

B  C  A, C  A  B,

that favors A over B. Adding this conﬁguration, depicted by the x values in Fig-

ure 22.4a,hasnoeﬀect on the positional rankings (each candidate receives the same

x + xs bonus points). Figure 22.4a shows that the pairwise tallies are:

A : B with 1 + 2x :2+x, A : C with 3 + x :2x, B : C with 3 + 2x : x.

Thus A is the Condorcet winner with an x value satisfying

1+2x > 2+x, 3+x > 2x,

or x = 2. These new terms aﬀect the pairwise outcomes but not the positional or

Borda outcomes.

donald g. saari 403

Next, add “conﬁgurations of preferences” to alter the positional outcomes but

not the Borda and pairwise outcomes. According to the above, we must add NRR

reversal terms. To make C the plurality winner, add (see Figure 22.4b) y units of

(A  B  C, C  B  A)andz units of (C  A  B, B  A  C). According to

Figure 22.4b, the plurality (s = 0) tallies for A: B: C are 1 + y :2+z : y + z.Sothe

C  B  A plurality ranking occurs with y and z values satisfying:

y + z > 2+z > 1+y.

One solution has y = z = 3; along with the above x = 2, they create the Chair proﬁle.

Only the Borda Count satisﬁes both NRR and NCR, so only this rule is immune

to these perturbations: the Borda ranking remains B  A  C.Noticethatwe

could have selected any ranking for the plurality method and created a supporting

proﬁle.

Some consequences. Several consequences follow from this construction including

the historical debate whether the Condorcet or Borda winner better reﬂects the voters’

beliefs. As indicated above, all possible diﬀerences in the Borda and Condorcet winners

are caused by Condorcet terms! (This statement holds for any number of candidates.)

Consequently, this two-century debate reduces to determining the appropriate out-

come for the Condorcet triplet. Namely, if you support the Condorcet winner, then

you must explain why the Condorcet triplet outcome should not be a tie. As I

have never heard a convincing argument, I must support the Borda winner. This

comparison of Borda and Condorcet winners is illustrated with the construction of

the Chair election example where the bias introduced by Condorcet triplet changes

the Condorcet winner from B to A

As another example, there are many papers that analyze whether a procedure must

elect the Condorcet winner. To understand the results, notice from NRR that any non-

Borda positional procedure, or rules using these positional procedures, cannot satisfy

this condition because their outcomes are changed by adding proﬁle portions with

no eﬀect on pairwise outcomes. (This comment is illustrated by the construction of

the Chair example.) Because the Condorcet winner can be altered by using Condorcet

triplets (or Condorcet n-tuples for n ≥ 3 candidates), only those procedures based on

pairwise outcomes can possibly satisfy this condition.

6 Strategic and Other Behavior

.............................................................................

The important Gibbard–Satterthwaite theorem (Gibbard 1973; Satterthwaite 1975)

shows that with three or more candidates, all “reasonable” election methods (e.g.

where each candidate can be elected and we exclude dictatorial rule) allow settings

where it is to the advantage of some voter to vote “strategically” rather than sincerely.

By doing so, the voter ensures a personally better election outcome. But we know

this; for instance, had more Nader voters voted strategically for Gore in Florida,

404 a tool kit for voting theory

we would have President Gore instead of President Bush. Beyond strategic voting,

there are many other peculiarities; e.g. Fishburn and Brams (1983) showed that

with a plurality run-oﬀ system, situations occur where a voter obtains a personally

better election outcome by not voting. Other fascinating examples and problems

have been discovered; e.g. with the plurality run-oﬀ, a winning candidate could lose

by receiving more votes. One of the better references describing these diﬃculties is

Nurmi (2003).

In Saari (1994), I constructed an argument to explain all of these behaviors and to

determine whether a speciﬁc procedure experiences any of these problems, when this

can occur, and how to cause the changed outcome. While it answered the questions,

it was technical. So, recently I developed a simpler equivalent approach (Saari 2003).

While the explanation is in Saari (2003), let me illustrate the ideas with {Anni, Lillian,

Katri} denoted by A, L,andK . If a proﬁle (say, the sincere proﬁle) elects Anni, but an

altered form of this proﬁle (say, strategic behavior, or someone not voting, or more

voters now supporting Anni, or ...)electsKatri,theninsomesensethechanged

proﬁle moved over the tied Katri–Anni region. Thus, the approach emphasizes tied

outcomes as follows:

1. For a given rule, ﬁnd all scenarios with a nearly tied outcome in some election.

2. Determine how the ﬁnal outcome changes by breaking the tie in diﬀerent ways.

3. Determine who could vote diﬀerently to break the tie and beneﬁt from the new

conclusion.

To illustrate, consider a positional election run-oﬀ election with the L  A  K

outcome so A and L advance to the run-oﬀ where L beats A to win. Now suppose

A and K are nearly tied; e.g. the election outcome is nearly L  A ∼ K .Ifachange

allows K to edge ahead of A, the run-oﬀ is between L and K .IfK beats L in the

run-oﬀ, then any way that alters the Anni–Katri near-tie alters the ﬁnal outcome.

Proﬁles with this behavior exist; we know this from the above “dictionary approach”

describing all lists of election rankings. This discussion shows that many proﬁles

deﬁne the positional outcome

(L 

A ∼ K , L  A, K  L , K  A)

where a slight change in the proﬁle, one way or another, breaks the positional tie

and retains the pairwise outcomes. To beneﬁt by such actions a voter must prefer

K  L. But to vote strategically for Katri over Anni, he must sincerely prefer A  K .

Consequently, the only voter in this scenario that could alter the outcome has

A  K  L preferences and strategically votes either K  A  L or K  L  A to

force the Lillian and Katri run-oﬀ rather than Anni and Lillian. To create illustrating

proﬁles, use the method in the previous section.

If a voter fails to vote and the outcome changes in his favor, he would have voted for

Anni over Katri: he prefers A  K . For the Katri outcome, rather than Lillian, to be

personally better, he prefers K  L .Hence,onlyanA  K  L voter could beneﬁt

by not voting. In this simple manner, all of these voting anomalies can be understood

and analyzed.

donald g. saari 405

7 Arrow and Sen

.............................................................................

The seminal Arrow’s (1951)andSen’s(1970a) theorems have rightfully played a major

role in shaping the direction of social choice over the last half-century: both show

that assumptions we assume are innocuous, are not. The general interpretation is

that these theorems mean that “no decision rule is fair.” But this is not the case: both

Arrow’s and Sen’s theorems admit surprisingly benign interpretations that make it

possible to ﬁnd ways to sidestep their conclusions. While the details are described in

Saari (2001b), it is worth developing some intuition to understand at least Arrow’s

result. Related arguments explain Sen’s result, which claims there can be serious

conﬂicts between individual rights and unanimity, and I refer the interested reader to

Saari (2001b). I also suggest Saari and Petron (2006) to see a surprising interpretation

that, rather than an infringement on individual rights, Sen’s result could represent a

dysfunctional society.

Treat Arrow’s theorem as describing the inputs (voters’ preferences), outputs

(election ranking), and election rule. For inputs, assume that each voter has a com-

plete, transitive ranking of the alternatives with no restrictions. For outputs, assume

that the societal ranking is transitive. For the election rules, assume (a unanimity

over a pair condition) that when everyone has the same ranking of a particular pair,

that ranking is the societal outcome: this is called the Pareto condition. After all,

if everyone prefers Alice to Carol, we should rebel against a Carol  Alice societal

ranking.

To motivate the last condition, suppose a prize committee announces their Alice 

Beth  Carol ranking with Alice as the winner. Imagine the reaction from Beth’s

supporters if they discover that if more committee members had a better opinion

of Carol, Beth would have won! What does Carol have to do with the {Alice, Beth}

ranking? So binary independence (or independence of irrelevant alternatives) asserts

that a pair’s societal ranking depends strictly on what the voters think of this particu-

lar pair: all other information is irrelevant.

While seemingly innocuous, Arrow proved that with three or more alternatives,

the only decision rule satisfying these conditions is a dictator! An explanation why

this occurs and how to sidestep the conclusion is in Saari (2001b). Here I oﬀer a new

intuitive explanation. But ﬁrst, let me oﬀer an example that builds on experiences all

academics have shared with those ballots asking us to vote for one candidate from

each school of an university. To simplify the numbers, suppose that three deans are

to select a student judiciary committee, where, for obvious reasons, each dean must

vote for one of the two candidates from each school. Let the candidates be:

Sciences

Engineering Arts

Alice Connie Elaine

Barb

Diane Florence

(8)

Suppose by a 2 : 1 vote, the elected committee is {Alice, Connie, Elaine}. To determine

whether this outcome is appropriate, consider all possible voter preferences. Four

406 a tool kit for voting theory

have one voter preferring one set of candidates, another preferring the opposite

committee, and the third voter breaks the tie with his {Alice, Connie, Elaine} choice:

it is diﬃcult to argue against the outcome here. The last possibility has the voter

preferences {Alice, Connie, Florence}, {Alice, Diane, Elaine}, and {Barb, Connie,

Elaine}. But even here the outcome is supported by 2 : 1 votes.

To introduce doubt, suppose the last possibility is the actual vote and it captures the

voters’ intent to include at least one candidate from the top and bottom lines; maybe

these lines are distinguished by race and the deans wanted a mixed-race committee:

Sciences Engineering Arts

Black Alice Connie Elaine

White

Barb Diane Florence

(9)

If so, then even though each voter voted consistently with this objective, the outcome

violated their intent. This undesired choice is no surprise because the pairwise vote,

and any binary independence rule, only examines a particular pair. It cannot, and

does not, reﬂect intended relationships among the pairs. It is unrealistic to expect a

voting rule that satisﬁes binary independence to do this extra duty.

Now alter the example with a name change involving the binary rankings

of A, B, C. Namely replace Alice with A  B, Barb with B  A, Connie with

B  C,DianewithC  B, Elaine with C  A, and Florence with A  C. With

this name change, the “mixed-race rankings” become transitive rankings,whilethe

“single race committees” are cyclic rankings. Moreover, the voter rankings {Alice,

Connie, Florence}, {Alice, Diane, Elaine}, and {Barb, Connie, Elaine} become the

Condorcet triplet {A  B  C, B  C  A, C  A  B}. Because the two exam-

ples diﬀer only by a name change, any comment about the dean selection problem

applies to voting over pairs. In particular, because binary independence strips any

mixed-race intended relationship from the ﬁrst problem, Arrow’s theorem occurs

because binary independence strips away the intended “transitivity” relationship! (This

is made precise in Saari 2001b.)

By recognizing that binary independence strips away the intended transitivity

relationship from preferences, we can rectify the problem: ﬁnd ways to reintroduce

the transitivity information. By doing so, positive assertions are forthcoming; e.g. the

Borda Count replaces Arrow’s dictator. Incidentally, a similar explanation holds for

Sen’s theorem.

8 Conclusion

.............................................................................

The message of this chapter is that the beautiful results in voting theory and social

choice can add an important dimension to our understanding of the strengths and

weaknesses of decision rules. While a technical understanding is helpful, it is not

necessary. Even developing a basic intuition, which I tried to provide, can eliminate

misinterpretations and help us address more subtle election properties.

donald g. saari 407

References

Arrow,K.1951. Social Choice and Individual Values.NewYork:Wiley(2nd edn. 1963).

Brams,S.,andFishburn,P.1983. Approval Voting. Boston: Birkhauser.

Fishburn,P.1981. Inverted orders for monotone scoring rules. Discrete Applied Mathematics,

3: 27–36.

and Brams,S.1983. Paradoxes of preferential voting. Mathematics Magazine, 56: 207–14.

Gibbard,A.1973. Manipulation of voting schemes: a general result. Econometrica, 41: 587–601.

Nurmi,H.2003. Voting Procedures under Uncertainty.NewYork:Springer-Verlag.

Saari,D.G.1989. A dictionary for voting paradoxes. Journal of Economic Theory, 48: 443–75.

1990. The Borda Dictionary. Social Choice and Welfare, 7: 279–317.

1994. Basic Geometry of Voting.NewYork:Springer-Verlag.

1995. A chaotic exploration of aggregation paradoxes. SIAM Review, 37: 37–52.

1999. Explaining all three-alternative voting outcomes. Journal of Economic Theory,

87: 313–35.

2000. Mathematical structure of voting paradoxes. Economic Theory, 15: 1–101.

2001a. Chaotic Elections! A Mathematician Looks at Voting.Providence,RI:American

Mathematical Society.

2001b. Decisions and Elections: Explaining the Unexpected.NewYork:CambridgeUniver-

sity Press.

2003. Disturbing aspects of voting theory. Economic Theory, 22: 529–56.

and Petron,A.2006. Negative externalities and Sen’s liberalism theorem. Economic

Theory.

and van Newenhizen,J.1988. Is Approval Voting an “unmitigated evil?” Public Choice,

59: 133–47.

Satterthwaite,M.1975. Strategyproofness and Arrow’s conditions. Journal of Economic

Theory, 10: 187–217.

Sen,A.1970a. The impossibility of a Paretian liberal. Journal of Political Economy, 78: 152–7.

1970b. Collective Choice and Individual Welfare. San Francisco: Holden Day.

Tabarrok,A.2001, Fundamentals of voting theory illustrated with the 1992 election, or could

Perot have won in 1992? Public Choice, 106: 275–97.

and Spector,L.1999. Would the Borda Count have avoided the civil war? Journal of

Theoretical Politics, 11: 261–88.

chapter 23

..............................................................

INTERPERSONAL

COMPARISONS OF

WELL-BEING

..............................................................

charles blackorby

walter bossert

1 Introduction

.............................................................................

This chapter provides a brief survey of the use of interpersonal comparisons in

social evaluation. We focus on principles for social evaluation that are welfarist (Sen

1979): principles that use information about individual well-being to rank alterna-

tives, disregarding all other information. Utility functions are indicators of individual

well-being and we use the terms utility and well-being synonymously. Sentient non-

human animals have experiences and it is possible to take account of their interests in

social evaluation. We focus on human beings in this chapter and refer the interested

reader to Blackorby and Donaldson (1992) for a discussion of the ethics of animal

exploitation.

We begin with the idea that a society has a number of options from which to choose

those that are “best” in some sense. This requires that the society be able to rank

the options according to their social goodness. We call these options alternatives; an

alternative is a complete description of everything that matters to society. Of course,

each individual member of this society can also rank these alternatives in terms of

∗

We thank Barry Weingast and Donald Wittman for comments and suggestions. Financial support

through a grant from the Social Sciences and Humanities Research Council of Canada is gratefully

acknowledged.

charles blackorby & walter bossert 409

their goodness for herself or himself; in fact, we assume that each individual has

a utility function that is an indicator of his or her well-being experienced in the

alternatives. A list of utility functions, one function for each individual, is called a

utility proﬁle. The social ranking is to be determined by a social evaluation functional.

A social evaluation functional associates a social ordering of the alternatives with

every utility proﬁle in its domain. Welfarism obtains if and only if there exists a social

evaluation ordering of vectors of individual utilities that can be used, together with

the information about well-being in a proﬁle, to rank the alternatives.

Welfarist principles regard values such as individual liberty and autonomy as

instrumental: valuable because of their contribution to well-being. Because of this, it

is important to employ a comprehensive notion of well-being such as that of Griﬃn

(1986). Individuals who are autonomous and fully informed may have self-regarding

preferences that accord with their well-being, but we do not assume that they do. If

they do, the individual utility functions are representations of these preferences.

Welfarism rests mainly on the view that any two alternatives in which everyone

is equally well oﬀ are equally good, a condition that is called Pareto indiﬀerence.

The Pareto indiﬀerence axiom is implied by a condition proposed by Goodin (1991).

Goodin suggests that if one alternative is declared socially better than another, then

the former should be better than the latter for at least one member of society. This

is a fundamental property of a principle for social evaluation and we consider it a

strong argument in favor of welfarism. Without this requirement, we run the risk

of recommending social changes that are empty gestures, beneﬁting no one and,

perhaps, harming some or all.

Because Pareto indiﬀerence applies separately to each utility proﬁle, we need a

way to require a principle for social evaluation to behave consistently across diﬀerent

proﬁles. Such a condition is provided by the axiom binary independence of irrelevant

alternatives. We say that two utility proﬁles coincide on an alternative x if each

individual’s utility of x is the same in both proﬁles. The independence axiom requires

that if two proﬁles coincide on an alternative x and on an alternative y, then the social

ranking of x and y must be the same for both proﬁles.

The most commonly employed domain of a social evaluation functional consists

of all logically possible utility proﬁles. On this unlimited domain, a social evaluation

functional satisﬁes Pareto indiﬀerence and binary independence of irrelevant alterna-

tives if and only if it is welfarist.

Arrow’s (1951) fundamental theorem states that there do not exist satisfactory

welfarist principles if the only information that can be used in social evaluation is

ordinally measurable and interpersonally non-comparable utility information. Sen

(1970) shows that the conclusion of Arrow’s theorem remains true if Arrow’s ordinal

interpretation of individual utility is replaced by a cardinal interpretation and no

interpersonal comparisons of well-being are permitted. Taking these results as our

starting point, we illustrate how the Arrow–Sen impossibility can be avoided if vari-

ous forms of interpersonal utility comparisons are possible.

Information invariance conditions require that the social evaluation principle

respect the informational environment regarding the measurability and interpersonal

410 interpersonal comparisons of well-being

comparability of well-being. The term measurability refers to the informational con-

tents of individual utility functions and, therefore, is concerned with intrapersonal

comparisons of well-being only. In contrast, interpersonal comparability speciﬁes the

kind of comparisons that can be made across diﬀerent individuals.

Two types of measurability assumptions are employed—ordinal measurability and

cardinal measurability. If utilities are ordinally measurable, the only information that

can be used is information regarding the ranking of the alternatives with respect to

their goodness for an individual. Thus, if a utility function is used as a representation

of an individual goodness ranking, any utility function that preserves the ranking

of alternatives can be used without changing the available information. Because any

increasing transformation of a utility function represents the same ranking as the

original function, it follows that statements such as “individual i is better oﬀ in

alternative x than in alternative y” are meaningful because they are preserved by

all increasing transformations of i’s utility function. In the case of ordinal measur-

ability, an individual utility function is unique up to increasing transformations—all

increasing transformations (and only those) preserve the informational contents of

the utility function. Ordinal measurability does not permit us to perform intraper-

sonal comparisons of utility diﬀerences. This is guaranteed by cardinal measurability.

A cardinal utility function is unique up to increasing aﬃne transformation, that

is, transformations whose graphs are positively sloped straight lines. In that case,

it follows that statements such as “individual i’s diﬀerence in well-being between

alternatives x and y is greater than the diﬀerence in i’s well-being between z and

w” are meaningful because they are preserved by all admissible transformations in

this informational environment.

Measurability assumptions are silent regarding the interpersonal comparability

of utilities. To specify what types of comparisons can be carried out across indi-

viduals, these assumptions have to be combined with interpersonal comparability

requirements. The assumptions we consider in this chapter are ordinal and cardinal

non-comparability and, in addition, ordinal and cardinal full comparability. Ordinal

and cardinal non-comparability are informational environments that do not allow

for any interpersonal comparability. They allow admissible transformations to be

independent across individuals and, thus, the only meaningful statements are the

intrapersonal comparisons permitted by the corresponding measurability assump-

tion. Ordinal and cardinal full comparability impose restrictions on admissible trans-

formations across individuals. In particular, if utilities are ordinally measurable and

interpersonally fully comparable, the only transformations that can be applied are

increasing transformations that are common for all individuals. Thus, interpersonal

comparisons of utility levels such as “individual i is better oﬀ in x than individual j

in y” are possible because all these comparisons are preserved if the same transforma-

tion is applied to all utilities. In the case of cardinal full comparability, only increasing

aﬃne transformations that are the same for all individuals can be applied and, as

a consequence, not only utility levels but also utility diﬀerences are interpersonally

comparable. This is the case because statements such as “the diﬀerence between

individual i’s utility in alternative x and j ’s utility in y is greater than the diﬀerence

charles blackorby & walter bossert 411

between k’s utility in z and ’s utility in w” are preserved if any common increasing

aﬃne transformation is applied to all individuals’ utilities.

As is standard in the literature, we express information assumptions by specifying

the transformations that can be applied to utility proﬁles without changing their

informational contents. If two utility vectors u =(u

,...,u

)andv =(v

,...,v

)

are subjected to a vector of admissible transformations under a given informational

environment, information invariance with respect to that environment demands that

the social ranking of the transformed vectors is the same as that of u and v.

We review some of the most important characterization results for welfarist social

evaluation principles. Due to space limitations, we cannot provide an exhaustive

survey but we attempt to mention the most relevant references for further reading.

For the same reason, we do not provide any proofs but refer the interested reader to

the original contributions or more extensive surveys.

Section 2 introduces our basic notation along with a formal deﬁnition of social

evaluation functionals. In addition, we present the welfarism theorem which shows

that welfarism is a consequence of three fundamental axioms. Because welfarism

permits us to work with a single ordering of utility vectors (called a social evaluation

ordering), this ordering is employed instead of the social evaluation functional in

the remainder of the chapter. In Section 3, we formulate some basic axioms for social

evaluation orderings and deﬁne the orderings that are of particular importance in this

chapter. Information invariance properties are introduced in Section 4,andSection5

contains an overview of some important results. Section 6 concludesthechapterwith

a discussion of possible extensions and applications of our model in choice problems.

2 Welfarist Social Evaluation

.............................................................................

Consider a society of at least two individuals. There is a set of at least three alternatives

and a principle for social evaluation is supposed to rank these alternatives on the basis

of the utilities of the members of this society. Individual i’s well-being is represented

by a utility function U

that assigns a level of utility (well-being) to each of the alter-

natives. Thus, U

(x)isi’s well-being in alternative x. Suppose there are n individuals.

A utility proﬁle is a vector U =(U

,...,U

) of individual utility functions, one for

each individual i.

A social evaluation functional assigns a social ranking of alternatives to each proﬁle

of utility functions in its domain. Thus, the social ranking depends on the utility

proﬁle. The domain of the social evaluation functional is the set of all proﬁles for

which the functional is supposed to generate a social ordering. Although we will im-

pose an unlimited-domain assumption requiring that the social evaluation functional

produces a social ranking for any logically possible proﬁle, we note that, in some

applications, it may make sense to restrict this domain. For example, in economic

environments where the alternatives are allocations of commodity bundles, it is