Яковлев Н.В. и др. Практикум по высшей геодезии. Вычислительные работы

Подождите немного. Документ загружается.

для длины стороны 4—5

1/Р

в4б

= (—1,00 0,09 1,00 -~-°'

)Х

0,02895 0,00486 0 0J246 —0,0

,1000

\ '

0,00486 0,01307 0,00708 —0,0

Ю027

\| °'

==() Q15

' 0,01246 0,00708 0,02117 —0,0

ю675

^—0,01000 —0,00027 —0,00675 0,С

И949

/ °»

С этими данными найдем по формул

(13.30) соответствующие

средние квадратические ошибки:

й5

= li УТЩь = 0,54 /О^* = 0,52";

Нь

jLi

VVр7

Л5

= 0,54 |/0ДП5 = °>07 дм = 0,007 м.

При определении обратного веса дирекционного угла и длины

диагонали между исходным пунктом 1 « определяемым пунктом 5

формула (13.31) запишется в виде соот

Ветственно

)(T)'

(,3

36)

ib \Q

QfcyJ

~=ы М. (13.37)

Взяв значения элементов весовой Матрицы из табл. 137

и вычислив по формулам (13.25), (13.26), используя координаты

пунктов 1 и 5, коэффициенты

а\ъ

= —2,§0; 6

=3,68; Cis = 0,80; rfis =

= 0,60, получим в соответствии с (13.30) и (13.37):

— = (—2,80 -J-3,68) ( °'°

2117

^.00675W-2,80N

®i5

^ 0,00675 ^01949/1+3,68/

1 I 0,02117 — 0 00675\ /4-0,80\

-5— = (+0,80 +0,60) ' =0,014.

*ib \—0,00675 0,>01949/ \+0,60/

С этими значениями обратных весс*Б вычислим средние квад-

ратические ошибки уравненного дирекционного угла и длины диа-

гонали 1—5.

та

1б

--=ц = 0,54 V^J69= 0,4Г;

*ib ~ Р У^ь

°'

КбТОМ ^ 0,06 дм = 0,006 м.

Аналогичным образом можно вычалить средние квадратиче-

ские ошибки и других элементов уравт^нной сети.

Средние квадратические ошибки од**их и тех же элементов, вы-

численные с использованием обратный весов, найденных из реше-

ния системы нормальных уравнений пс* схеме Гаусса, и с использо-

ванием матрицы весовых коэффициентов* получают одни и те же

значения, как и должно быть согласР

теории. В этом можно

убедиться, сравнив дважды вычислен/

значения средних квад-

ратических ошибок: т

а45

, т

$АЪ

, т

Хь

Уъ•

Заключительным этапом уравните^

ьных

вычислений является

составление каталога координат.

239

Общие сведения об уравнивании комбинированных геодезиче-

ских сетей. Под комбинированной сетью понимается сеть, на раз-

ных участках которой положение пунктов определяется различ-

ными методами, например, методами триангуляции, полигономет-

рии или трилатерации, в той или иной их комбинации. Схема

построения таких сетей в каждом конкретном случае разрабаты-

вается особо.

Комбинированные геодезические сети можно рассматривать

как частный случай линейно-угловых сетей с измеренными в них

углами, длинами сторон и азимутами. Уравнивание их может вы-

полняться как коррелатным, так и параметрическим способом.

Прежде чем приступить к уравниванию, требуется определить

веса угловых и линейных измерений, пользуясь формулами (13.4).

При коррелатном способе уравнивания в сети могут возник-

нуть условные уравнения фигур, полюсные, дирекционных углов

и сумм углов, базисные и условия сторон, абсцисс и ординат. Из

уравнивания должны определяться поправки к измеренным на-

правлениям (и

) и длинам сторон (v

) под условием [p

] +

+ [psv

]= min.

Параметрический способ уравнивания более предпочтителен

вследствие его простого алгоритма, легко реализуемого на ЭВМ.

В комбинированных геодезических сетях составляются уравнения

поправок двух видов — для измеренных направлений и для изме-

ренных длин сторон, с учетом весов измерений.

Составлению уравнений поправок предшествует вычисление

предварительных координат пунктов, решение обратных геодези-

ческих задач по всем сторонам сети, вычисление коэффициентов и

свободных членов уравнений поправок и т. п. Последовательность

уравнительных вычислений остается такой же, как и в линейно-

угловой сети.

Если в комбинированной геодезической сети есть исходные ди-

рекционные углы (азимуты Лапласа) и базисные стороны, то к

уравнениям поправок направлений и поправок сторон присоеди-

няют условные уравнения дирекционных углов и базисные. Все

вместе взятые уравнения поправок и условные уравнения решают

совместно по методу наименьших квадратов.

Глава 14

УРАВНИВАНИЕ ТРИАНГУЛЯЦИИ

ПО ДВУХГРУППОВОМУ МЕТОДУ Н. А. УРМАЕВА

§ 78. Общие сведения об уравнивании триангуляции

по углам

Для того чтобы уменьшить число нормальных уравнений, воз-

никающих в сети, триангуляцию нередко уравнивают не по нап-

равлениям, как это требуется, а по углам. При параметрическом

240

способе уравнивания углов уменьшается число уравнений попра-

вок на пунктах, а также общее число непреобразованных нормаль-

ных уравнений в сети.

Пусть на пункте измерены направления 1.2 и 1.3, образующие

угол р (рис. 62). Для направлений уравнения поправок имеют

вид

t>13

= -

013?!

— + вхз£з +

13Ъ + I

Обозначив —V\2 и сделав соответствующие подстановки,,

получим уравнения поправок для углов 0:

(^1з —

1г)

h —

(

i3 — ^12) Лх —

izh

— 612Л2

«1353

+ ^3 + ^, (14.2У

где /р = а°

— а°

—

Здесь р'— измеренное значение угла. Дирекционные углы а

и ко-

эффициенты а, Ь вычисляются по приближенным координатам

пунктов по формулам (10.2) и (10.6) соответ-

ственно.

На каждом пункте число уравнений попра-

вок углов (14.2) на единицу меньше числа я

уравнений поправок направлений (14.1). В

уравнениях поправок углов (14.2) отсутству-

ют поправки 8z ориентирования направлений

на станции (они исключаются). Поэтому в се- РИС. 62

ти из п пунктов, на которых исполнены угло-

вые измерения, число нормальных уравнений при уравнивании

углов будет на п меньше, чем при уравнивании направлений.

При уравнивании триангуляции параметрическим способом па

углам состав и последовательность вычислительных операций ос-

таются такие же, как и при уравнивании направлений (см, гла-

ву 9), исключая преобразования по составлению редуцированных

нормальных уравнений.

Отметим, что в одной и той же сети число редуцированных

нормальных уравнений при уравнивании направлений равно числу

нормальных уравнений при уравнивании в ней углов и равно уд-

военному числу вновь определяемых пунктов. Таким образом, при

параметрическом способе экономический эффект от уравнивания

углов вместо направлений невелик, а последствия этого ощутимы,,

о чем следует помнить, особенно при обработке сетей повышенной:

точности.

Экономические достоинства уравнивания триангуляции по уг-

лам на ЭКВМ наиболее ощутимы при использовании двухгруппо-

вого метода, усовершенствованного Н. А. Урмаевым.

При уравнивании триангуляции по методу Урмаева условные

уравнения делят на две группы. В первую группу включают усло-

вия фигур неперекрывающихся треугольников, во вторую — остав-

шиеся условия фигур, горизонта, полюсные, дирекционных углов,

базисные и координат. Поскольку при уравнивании углов услов-

16-2296

241

ные уравнения первой группы не имеют общих поправок (не зави-

сят друг от друга), то решение их по методу наименьших квадра-

тов сводится к распределению невязки с обратным знаком поров-

ну во все углы треугольника.

Поправки углов v\ полученные из решения уравнений первой

группы, называют первичными. Вторичные поправки v" в углы

находят после решения уравнений второй группы.

Решение условных уравнений второй группы требует предва-

рительного преобразования их коэффициентов. Чтобы получить

преобразованный коэффициент при поправке в угол треугольника,

необходимо вычесть из непреобразованного коэффициента среднее

значение коэффициентов по данному треугольнику. Так что сумма

преобразованных коэффициентов по треугольнику и по сети в це-

лом равна нулю, что служит контролем их вычисления.

Вторичные поправки углов вычисляют по формуле

v{ = A

+ B

• • •

+ Dik

„, (14.3)

где Л, В и т. д. — преобразованные коэффициенты условных урав-

нений второй группы, к — коррелаты, полученные из решения пре-

образованных условных уравнений второй группы, г" — число ус-

ловных уравнений второй группы. Окончательная поправка в угол

равна сумме первичной и вторичной поправок:

vi^vt'+vi". (14.4)

§ 79. Определение числа условных уравнений.

Деление уравнений на группы

и решение уравнений первой группы

Уравнивание триангуляции по методу Урмаева рассмотрим на

примере сети триангуляции 3 класса, изображенной на рис. 63.

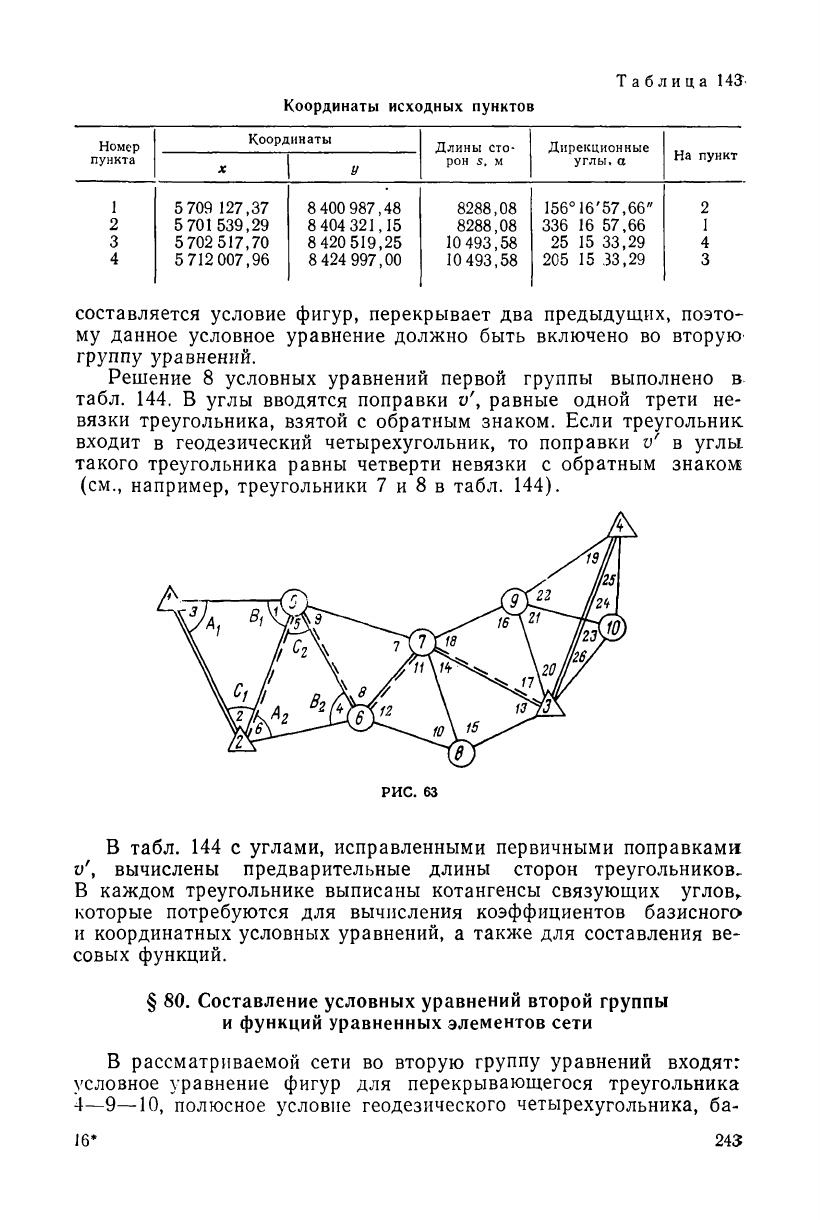
Координаты исходных пунктов 2 класса приведены в табл. 143.

Измеренные углы, редуцированные на плоскость, даны в табл. 144.

Число условных уравнений, возникающих в нашей сети при

уравнивании ее по углам, определим по формулам (9.3).

Всего S

= N*— 26 = 26— 26= 14;

фигур f = N — p — q+

= 26 —18 —0+1=9;

горизонта q = N + t

— £)

= 26 + 10 —36 = 0;

полюсных с = р

—

2я + 3=18 — 20 + 3=1;

базисных Гб = ^б —

= 2 —

= 1;

дирекционных углов г

= k

—

1=2—1 = 1;

абсцисс и ординат т

К%у

= 2 (k

xуУ

— 1) = 2х(2 — 1) = 2.

В сети возникает 9 независимых условий фигур, однако в пер-

вую группу войдут только 8: из них 6 простых треугольников и 2

для неперекрывающихся треугольников (3—4—9 и 3—4—10), вхо-

дящих в геодезический четырехугольник. Третий треугольник, на-

пример 4—9—10, для которого в геодезическом четырехугольнике

242

Таблица

109

Координаты исходных пунктов

Номер

пункта

Координаты

Длины сто-

рон 5, М

Дирекционные

углы, а

На пункт

Номер

пункта

Длины сто-

рон 5, М

Дирекционные

углы, а

На пункт

5 709 127,37

8 400 987,48

8288,08

156°16'57,66"

5 701 539,29

8 404 321,15

8288,08

336 16 57,66

5 702 517,70

8420519,25

10 493,58

25 15 33,29

5 712 007,96

8 424 997,00

10 493,58

205 15 33,29

составляется условие фигур, перекрывает два предыдущих, поэто-

му данное условное уравнение должно быть включено во вторую

группу уравнений.

Решение 8 условных уравнений первой группы выполнено в

табл. 144. В углы вводятся поправки v\ равные одной трети не-

вязки треугольника, взятой с обратным знаком. Если треугольник,

входит в геодезический четырехугольник, то поправки v' в углы

такого треугольника равны четверти невязки с обратным знаком

(см., например, треугольники 7 и 8 в табл. 144).

В табл. 144 с углами, исправленными первичными поправками

v\ вычислены предварительные длины сторон треугольников.

В каждом треугольнике выписаны котангенсы связующих углов,,

которые потребуются для вычисления коэффициентов базисного

и координатных условных уравнений, а также для составления ве-

совых функций.

§ 80. Составление условных уравнений второй группы

и функций уравненных элементов сети

В рассматриваемой сети во вторую группу уравнений входят:

условное уравнение фигур для перекрывающегося треугольника

4—9—10, полюсное условие геодезического четырехугольника, ба-

16*

243

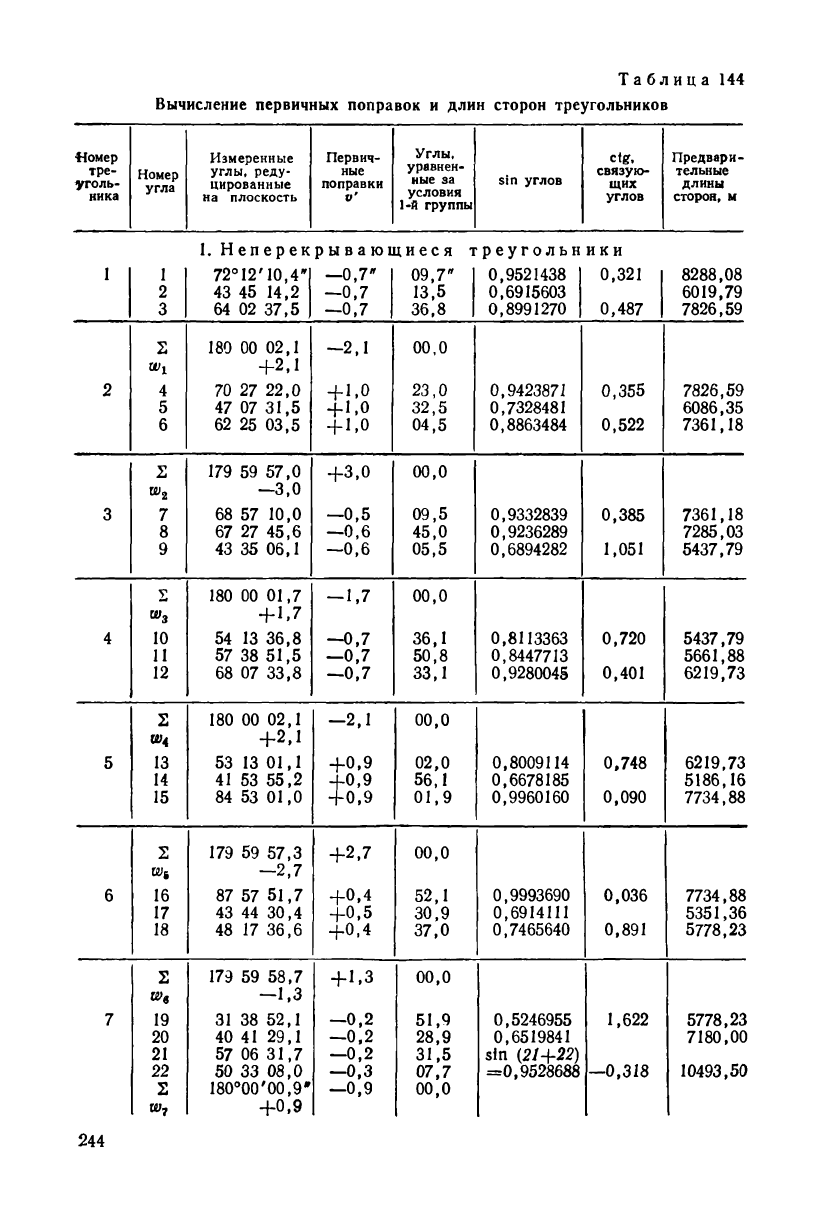
Таблица 126 Таблица

127

Вычисление первичных поправок

длин сторон треугольников

«омер

тре-

уголь-

ника

Номер

угла

Измеренные

углы, реду-

цированные

на

плоскость

Первич-

ные

поправки

Углы,

уравнен-

ные за

условия

1-й

группы

sin

углов

ctgr.

связую-

щих

углов

Предвари-

тельные

длины

сторон,

Неперек

72°12'10,4"

43 45 14,2

64 02 37,5

р ы в а юи

—0,7"

—0,7

ц и

ее я 1

09,7"

13,5

36,8

реугольн

0,9521438

0,6915603

0,8991270

ики

0,321

0,487

8288,08

6019,79

7826,59

180 00 02,1

+2,1

70 27 22,0

47 07 31,5

62 25 03,5

—2,1

+ 1,0

+1,0

00,0

23,0

32,5

04,5

0,9423871

0,7328481

0,8863484

0,355

0,522

7826,59

6086,35

7361,18

179 59 57,0

—3,0

68 57 10,0

67 27 45,6

43 35 06,1

+3,0

—0,5

—0,6

00,0

09,5

45,0

05,5

0,9332839

0,9236289

0,6894282

0,385

1,051

7361,18

7285,03

5437,79

180 00 01,7

+ 1.7

54 13 36,8

57 38 51,5

68 07 33,8

-1,7

—0,7

00,0

36,1

50,8

33,1

0,8113363

0,8447713

0,9280045

0,720

0,401

5437,79

5661,88

6219,73

180 00 02,1

+2.1

53 13 01,1

41 53 55,2

84 53 01,0

—2,1

+0,9

00,0

02,0

56,1

01,9

0,8009114

0,6678185

0,9960160

0,748

0,090

6219,73

5186,16

7734,88

179 59 57,3

—2,7

87 57 51,7

43 44 30,4

48 17 36,6

+2,7

+0,4

+0,5

+0,4

00,0

52,1

30,9

37,0

0,9993690

0,6914111

0,7465640

0,036

0,891

7734,88

5351,36

5778,23

179 59 58,7

-1,3

31 38 52,1

40 41 29,1

57 06 31,7

50 33 08,0

180°00'00,9

+0,9

+ 1,3

-0,2

—0,2

—0,3

—0,9

00,0

51,9

28,9

31,5

07,7

00,0

0,5246955

0,6519841

sin

(21+22)

=0,9528688

1,622

—0,318

5778,23

7180,00

10493,50

•244

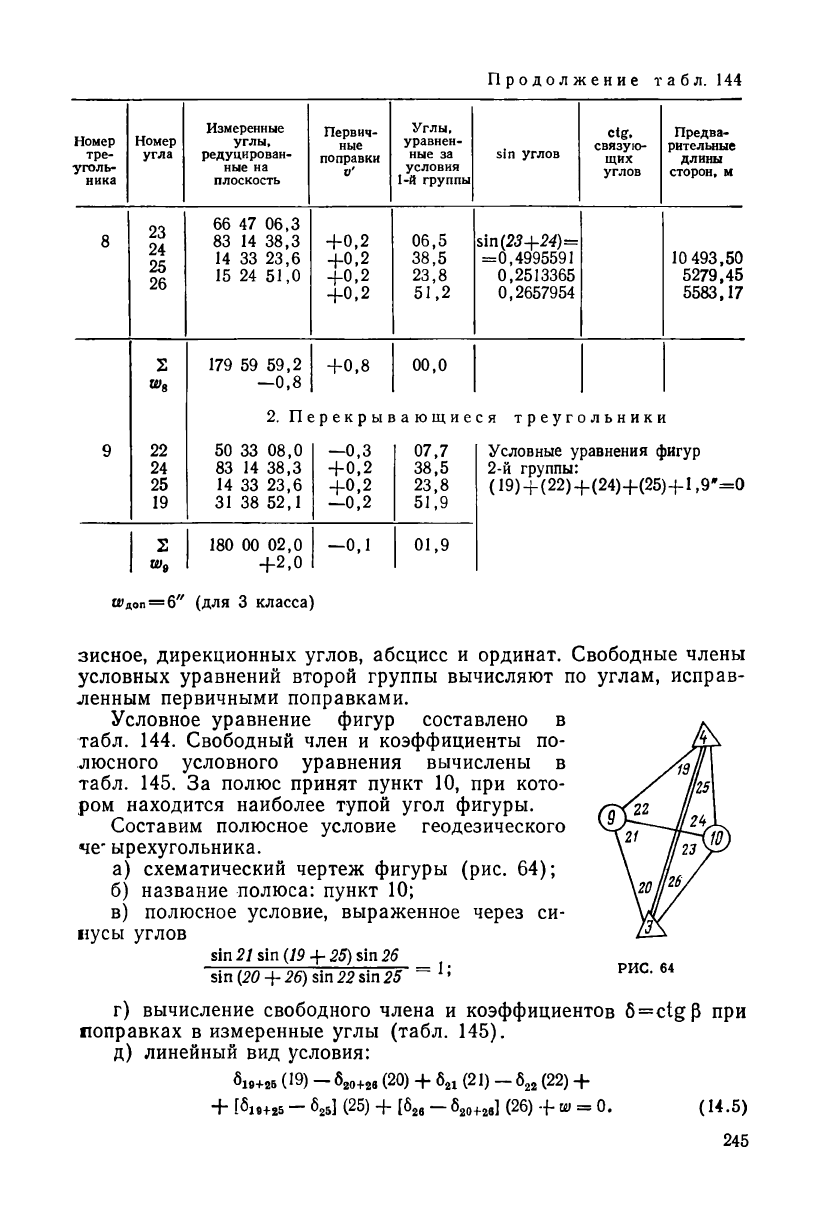
Продолжение табл. 144

Номер

тре-

уголь-

ника

Номер

угла

Измеренные

углы,

редуцирован-

ные на

плоскость

Первич-

ные

поправки

Углы,

уравнен-

ные за

условия

1-й группы

sin углов

ctgf.

связую-

щих

углов

Предва-

рительные

длины

сторон, м

66 47 06,3

83 14 38,3

14 33 23,6

15 24 51,0

+0,2

06,5

38,5

23,8

51,2

sin (23+24)=

=0,4995591

0,2513365

0,2657954

493,50

5279,45

5583,17

179 59 59,2

—0,8

+0,8

00,0

2. Перекрывающиеся треугольники

50 33 08,0

83 14 38,3

14 33 23,6

31 38 52,1

—0,3

+0,2

—0,2

07.7

38,5

23.8

51.9

Условные уравнения фигур

2-й группы:

(19) + (22)+(24)+(25)+1,9"=0

180 00 02,0

+2,0

—0,1

01,9

а>доп = 6" (для 3 класса)

зисное, дирекционных углов, абсцисс и ординат. Свободные члены

условных уравнений второй группы вычисляют по углам, исправ-

ленным первичными поправками.

Условное уравнение фигур составлено в

табл. 144. Свободный член и коэффициенты по-

люсного условного уравнения вычислены в

табл. 145. За полюс принят пункт 10, при кото-

ром находится наиболее тупой угол фигуры.

Составим полюсное условие геодезического

че* ырехугольника.

а) схематический чертеж фигуры (рис. 64);

б) название полюса: пункт 10;

в) полюсное условие, выраженное через си-

нусы углов

sin

(19

25)

sin

(20

26)

sin

sin 25 ~~

;

г) вычисление свободного члена и коэффициентов 6=ctgp при

поправках в измеренные углы (табл. 145).

д) линейный вид условия:

(19)- бго+гв (20) + 6

(21) — 6

(22) +

+ [6

lfl+25

- 6

] (25) + [6

2в

- 6

20+2в

] (26) + w - 0. (14.5)

245

Таблица

109

Числитель Знаменатель

Номер

угла

Углы Р

sin fi

ctg 3

Номер

угла

Углы ft

sin 0

ctg 0

19+25

57°06'31,5"

46 12 15,7

15 24 51,2

0,8397028

0,7218129

0,2657954

0,647

0,959

3,627

20+26

56°06'20,Г

50 33 07,7

14 33 23,8

0,8300666

0,7722031

0,2513365

0,672"

0,823

3,851

Г1|

= 0,1611008

Р «-М5

=0,1611017

2 ctg

р = 30,453

р = 20,7"

или с учетом 6 = ctg

0,959 (19) — 0,672 (20) + 0,647 (21)

—

0,823 (22)

—

2,892 (25) +

+ 2,955(26)— 1,15" = 0. (14.6)

Базисное условное уравнение возникает между исходными сто-

ронами S|

и 5з4- Используя углы, исправленные первичными по-

правками, II длину ИСХОДНОЙ стороны S12, ВЫЧИСЛИМ длину s'34 за-

данной стороны s

sin

(21

+ 22)

34 = s

sin

sin 4 sin

sin

Обозначив ctg p = запишем базисное условие в линейном

виде:

-«i (0 + (3) -

(4) + 6

(6) - 6-

(7)

+ 6

(9) - 8

(10)

+ 6

(12) -

1Э

(13) + 6

(15) - 6

1в

(16) + 6

(18) (19) +

+ W (21) + 6

21+22

(22) + иГ = 0, (14.8)

Р"

где w" = (s'

4~ ^34)'

Взяв из табл. 144 длину стороны 5'з4= 10 493,50 м, вычисленную

по углам, исправленным первичными поправками, а из табл. 143—

заданную длину этой же стороны s

= 10 493,58 м, найдем вели-

чину свободного члена

р"

206

265

и>"

= (S'a4 -

534)

= (10 493,50 - 10 493,58)

ют ьо

= —1,57".

и>"доп = 2,5 т

п2

2 ctg

р+ 2 ^ p'j" =

/ 2• 10

1,5^6,867 + 2 ( злоб") =Ю, Г,

где принято гпь/b—l:300000 и /п"=1,5".

246

Выписав из табл. 144 значения бр =ctgp, придадим базисно-

му условию окончательный вид

Условное уравнение дирекционных углов возникает между ис-

ходными дирекционными углами 021 и <хз4- Дирекционные углы пе-

редаются по ходовой линии, проходящей через вершины промежу-

точных углов С; на рис. 63 она показана пунктиром. Для наше-

го ряда условие дирекционных углов запишется в виде

где w = а'

—

з4

<а'з4 — вычисленное по углам С, исправленным первичными по-

правками, значение дирекционного угла а

Для определения свободных членов условия дирекционных уг-

лов и условий координат вычислим дирекционные углы и коорди-

наты пунктов ходовой линии (табл. 146).

В последней строке табл. 146 записаны промежуточные углы С

с их знаками, участвующие в передаче дирекционных углов по хо-

довой линии.

Ниже вычислены свободные члены условных уравнений дирек-

ционных углов и координат.

Дирекционный угол стороны 3.4:

Вычисленный а'

з4

= 25°15'36,56"

Заданный а

з4

= 25 15 33,29

Свободный член до =+3,27"

^доп = 2,5 + 2т

а =2,5 V^l,5

-7 + 2-1,1

= 10,7".

Для расчета допусков взято т"=1,5", т

= 1,1

—0,321 (1) + 0,487 (3)

—

0,355 (4) + 0,522 (6) — 0,385 (7) +

+ 1,051 (9) — 0,720 (10) + 0,401 (12) — 0,748 (13) +

+ 0,090 (15) — 0,036 (16) + 0,891 (18) — 1,622 (19) —

—

0,318 (21)

—

0,318 (22)

—

1,57" = 0.

(14.9)

(2)

— (5) + (8)

— (11) —

(14) + (17) + (20) + до = 0,

(14.10)

Координаты пункта 3:

Вычисленные

Заданные

Разности

= 5 702 517,55

=5 702 517,70

= —0,15

—

0,15

(/'3= 8 420 519,30

= 8 420 519,25

= +0,05

2.5 У

247

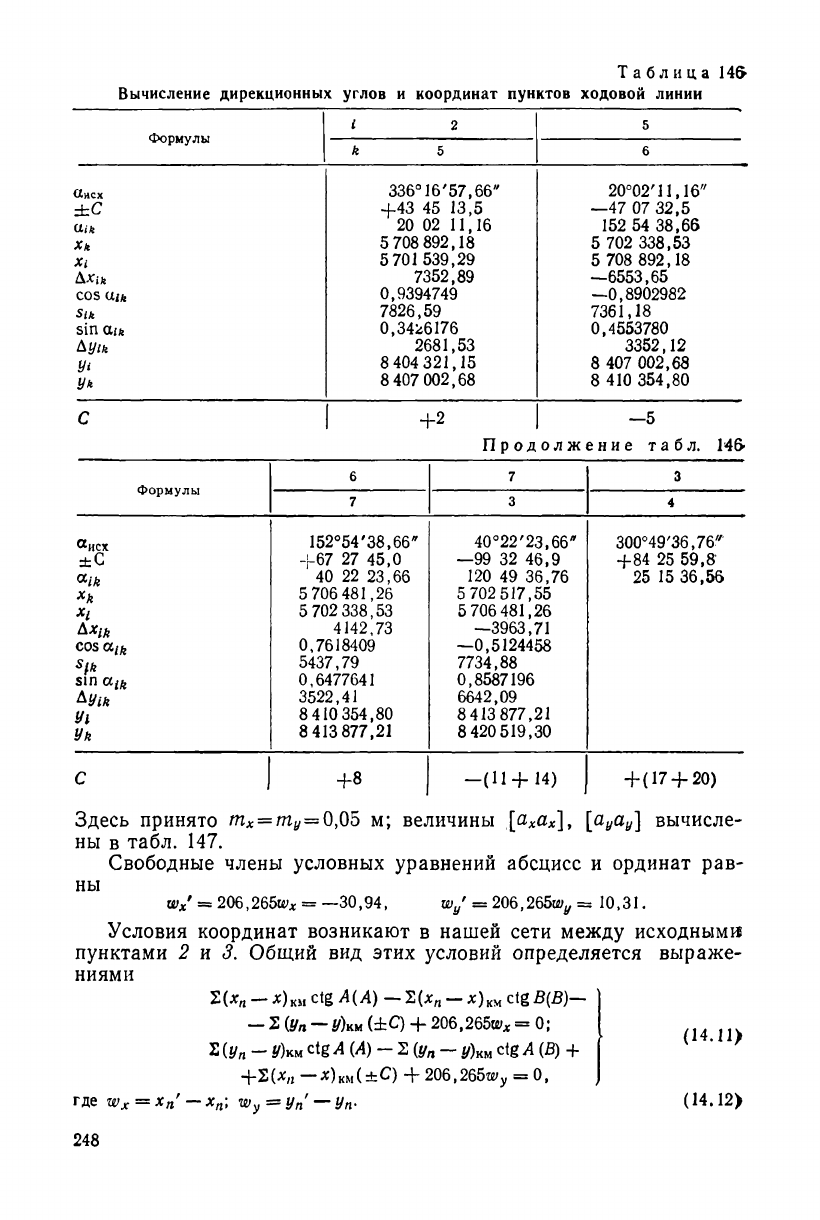
Таблица 146-

Вычисление дирекционных углов и координат пунктов ходовой линии

Формулы

О. исх

±с

Шк

COS

Щк

Sik

sin a;*

bytk

У1

У*

336°16'57,66"

+43 45 13,5

20 02 11,16

5 708 892,18

5 701 539,29

7352,89

0,9394749

7826,59

0,3426176

2681,53

8 404 321,15

8 407 002,68

20°02'11,16"

—47 07 32,5

152 54 38,66

5 702 338,53

5 708 892,18

—6553,65

—0,8902982

7361,18

0,4553780

3352,12

8 407 002,68

8 410 354,80

—5

Продолжение табл. 146-

Формулы

®исх

±с

<*ik

cos а

sin a

ЬУш

У1

Ук

152

54'38,66"

+67 27 45,0

40 22 23,66

5 706 481,26

5 702 338,53

4142,73

0,7618409

5437,79

0,6477641

3522,41

8 410 354,80

8 413 877,21

40°22'23,66"

—99 32 46,9

120 49 36,76

5 702 517,55

5 706 481,26

—3963,71

—0,5124458

7734,88

0,8587196

6642,09

8413877,21

8 420 519,30

300°49'36,76"

+84 25 59,8

25 15 36,56

+8 -(11 + 14)

+ (17 + 20)

Здесь принято т

= т

= 0,05 м; величины [йуйу] вычисле-

ны в табл. 147.

Свободные члены условных уравнений абсцисс и ординат рав-

ны

' = 206,265и>* = —30,94, w

' = 206,265w

= 10,31.

Условия координат возникают в нашей сети между исходными

пунктами 2 и <?. Общий вид этих условий определяется выраже-

ниями

2(*п

—

*)км ctg А(А) - Ъ(х

- *)

км

ctg

£(£)-

- s (Уп - у)км (±С) + 206,265= 0;

(Уп

У)км

ctg А (А) - 2 (у

~ у)

км

ctg А

(В)

+2 — х)

км

(± С) + 206,265w

= 0,

где w

= x

' — x

\ т

=Уп—Уп>

(14.11)

(14.12)

248