Яковлев Н.В. и др. Практикум по высшей геодезии. Вычислительные работы

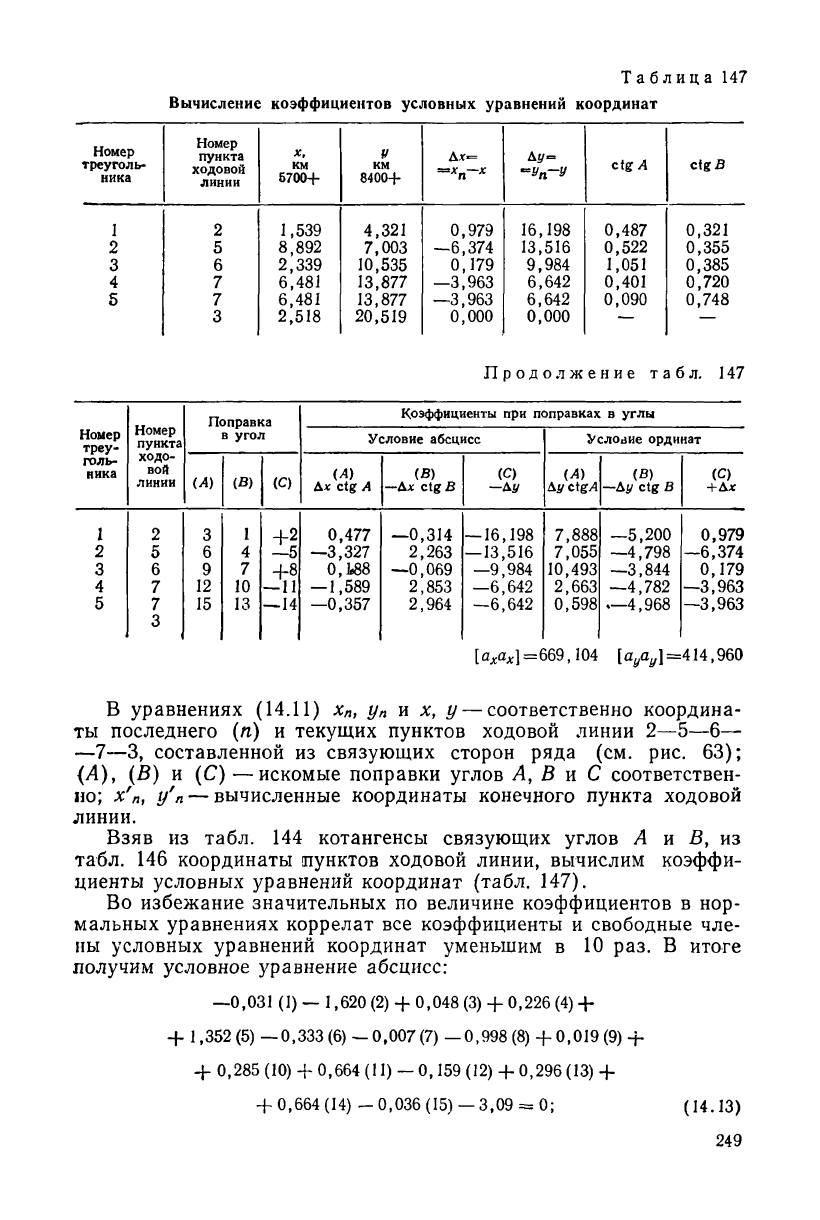
Таблица 147

Вычисление коэффициентов условных уравнений координат

Номер

треуголь-

ника

Номер

пункта

ходовой

линии

х,

км

5700+

У

км

8400-}-

Дх«= А у-

=у

п

-у

ctg А

ctg В

1

2

1,539 4,321 0,979

16,198

0,487

0,321

2 5

8,892

7,003

—6,374

13,516

0,522

0,355

3

6 2,339

10,535

0,179

9,984

1,051

0,385

4

7

6,481 13,877

—3,963

6,642

0,401

0,720

5

7

6,481

13,877 —3,963

6,642 0,090 0,748

3

2,518

20,519

0,000

—

Продолжение т а

б

л, 147

Номер

треу-

голь-

ника

Номер

пункта

ходо-

вой

линии

Поправка

в угол

Коэффициенты при поправках в углы

Номер

треу-

голь-

ника

Номер

пункта

ходо-

вой

линии

Поправка

в угол

Условие абсцисс

Условие ординат

Номер

треу-

голь-

ника

Номер

пункта

ходо-

вой

линии

(А)

(В)

(С)

(А)

Ддс

ctg

А

(В)

—Д*

ctg

В

(С)

-Д у

(А)

Ду c\gA

(В)

—Ду

ctg

В

(С)

+д*

1 2

3

1

+2

0,477

—0,314

—

16,198

7,888

—5,200

0,979

2

5

6

4

-5 —3,327

2,263 —13,516

7,055

—4,798

—6,374

3 6 9

7

+8

0,Ь88

—0,069 —9,984

10,493

—3,844 0,179

4

7

12

10

--11

—1,589 2,853 —6,642

2,663 —4,782

—3,963

5

7

3

15 13 —14 —0,357 2,964

—6,642 0,598

.—4,968 —3,963

[аде] =669,104 [а

у

а

у

\ =414,960

В уравнениях (14.11) х

п

, Уп и х, у — соответственно координа-

ты последнего (п) и текущих пунктов ходовой линии 2—5—6—

—7—3, составленной из связующих сторон ряда (см. рис. 63);

(А), (В) и (С)—искомые поправки углов А, В и С соответствен-

но; х'п, у'п — вычисленные координаты конечного пункта ходовой

линии.

Взяв из табл. 144 котангенсы связующих углов Л и В, из

табл. 146 координаты пунктов ходовой линии, вычислим коэффи-

циенты условных уравнений координат (табл. 147).

Во избежание значительных по величине коэффициентов в нор-

мальных уравнениях коррелат все коэффициенты и свободные чле-

ны условных уравнений координат уменьшим в 10 раз. В итоге

получим условное уравнение абсцисс:

—0,031 (1)

—

1,620 (2) + 0,048

(3)

+ 0,226

(4)

+

+ 1,352 (5)

— 0,333 (6)

—0,007(7) —0,998

(8)

+ 0,019 (9) +

+ 0,285 (10) + 0,664 (11)

—

0,159 (12) + 0,296

(13)

+

+ 0,664 (14) - 0,036 (15)

—

3,09 = 0; (14.13)

249;

Преобразование коэффициентов условных уравнений

Номер

треугольника

Номер

угла

Непреобразованные уравнения

Номер

треугольника

Номер

угла

(X

>»

ё

V

О

о

2

а

и

о

5

>»

X

а

X

X,

о

X

sf

tt

а>

а

s

tt

<1)

§

О

S

п

£

0

и

1

а

S3

я

S

о

ея

(А

1

2

3

+i

—0,321

+0,487

—0,031

— 1,620

+0,048

—0,052

+0,098

+0,789

—0,404

—0,522

+ 1,324

2

4

5

6

— 1

—0,355

+0,522

+0,226

+ 1,352

—0,333

—0,480

+0,637

+0,706

—0,609

+0,989

+0,895

3

7

8

9

+i

—

0,385

+ 1,051

—0,007

—0,998

+0,019

—0,384

+0,018

+ 1,049

—0,776

+0,020

+2,119

4

10

11

12

—1

—0,720

+0,401

+0,285

+0,664

—0,159

—0,478

+0,396

+0,266

—0,913

+0,060

+0,468

5

13

14

15

— 1

—0,748

+0,090

+0,296

+0,664

—0,036

—0,497

+0,394

+0,060

+

1

+0,748

—0,090

—0,201

+ 1,058

+0,024

6

16

17

18

+i

—0,036

+0,891

— 1

+0,036

-0,891

0,000

7 19

20

21

22

+ 1

+1

+0,959

—0,672

+0,647

—0,823

+i

—1,622

—0,318

—1

+ 1,622

+0,318

+ 1,959

—0,672

+0,647

+0,177

8 23

24

25

26

—2,892

+2,955

0,000

+ 1,000

—1,892

+2,955

ш

+1,90

—1,15

+3,27

— 1,57

—3,09

+1,03

250;

Таблица

187

второй группы

и

весовых функций

Преобразованные уравнения

Поправки

v

n

О.

£

X

•е-

<L>

О

К

О

2

ч

8

и

о

5

§

я

к

о

X

КГ

«

о

р.

к

п

0)

§

о

Я

т

СО

ю

и

Sf

о

со

Е-

СО

X

К

ч

а

о £

£ СО

Поправки

v

n

—0,333

+0,667

—0,333

—0,376

—0,055

+0,432

+0,503

— 1,086

+0,582

—0,330

—0,180

+0,511

—0,536

—0,654

+ 1,192

+0,7"

—0,7

0,0

+0,333

—0,667

+0,333

—0,411

—0,056

+0,467

—0,189

+0,937

-0,748

—0,768

+0,349

+0,418

-1,035

+0,563

+0,470

+0,6

+0,2

—0,8

—0,333

+0,667

—0,333

—0,607

—0,222

+0,829

+0,322

—0,669

+0,348

—0,612

—0,210

+0,821

— 1,230

—0,434

+ 1,665

+0,9

—0,8

—0,1

-

+0,333

—0,667

+0,333

—0,614

+0,106

+0,507

+0,022

+0,401

—0,422

—0,539

+0,335

+0,205

—0,798

+0,175

+0,623

—0,1

+0,3

—0,2

-

+0,333

—0,667

+0,333

—0,529

+0,219

+0,309

—0,012

+0,356

—0,344

—0,483

+0,408

+0,074

—0,333

+0,667

—0,333

+0,529

—0,219

—0,309

—0,495

+0,764

—0,270

—0,1

+0,3

—0,2

—0,333

+0,667

—0,333

—0,321

—0,285

+

0,606

+0,333

—0,667

+0,333

+0,321

+0,285

—0,606

0,000

0,0

-1,1

+ U

+0,500

—0,500

+0,500

+0,931

—0,700

+0,619

—0,851

—0,250

+0,750

—0,250

— 1,058

+0,564

+0,246

+0,250

—0,750

+0,250

+ 1,058

—0,564

—0,246

+1,431

— 1,200

+0,119

—0,351

— 1,4

+0,2

+0,9

+0,3

—0,500

+0,500

—0,500

—0,016

—2,908

+2,939

—0,516

+0,484

—2,408

+2,439

+0,4

—0,4

+0,4

+ 1,90

k—0,714

-1,15

+0,007

+3,27

-1,122

—1,57

+ 1,251

—3,09

+0,259

+ 1,03

-1,981

2р^

2

=:9,7

—Ikw

= 9,8

251

условное уравнение ординат:

—0,052 (1) + 0,098 (2) + 0,789 (3) — 0,480 (4) + 0,637 (5) + 0,0706 (6) —

— 0,384 (7) + 0,018 (8) + 1,049 (9) — 0,478 (10) + 0,396 (11) +

+ 0,266(12)— 0,497(13) +0,396(14) +0,060(15) + 1,03 = 0. (14.14)

Для оценки точности возьмем дирекционный угол и длину сто-

роны 7—8:

а

78

= а

з4

— 20 — 17+ 14 ± 180°,

sin

19

sin

16

sin 13

=

sin

(21

+ 22) sin

18

sin 15 '

и составим соответствующие им весовые функции

h — Да

78

= (14) —(17) — (20),

/

2

= As

78

= 0,748 (13) —0,090 (15) 4

-

0,036 (16)—

—0,891 (18) + 1,622 (19) + 0,318 (21) + 0,318 (22),

взяв котангенсы связующих углов из табл. 144.

§ 81. Преобразование и решение условных уравнений

второй группы

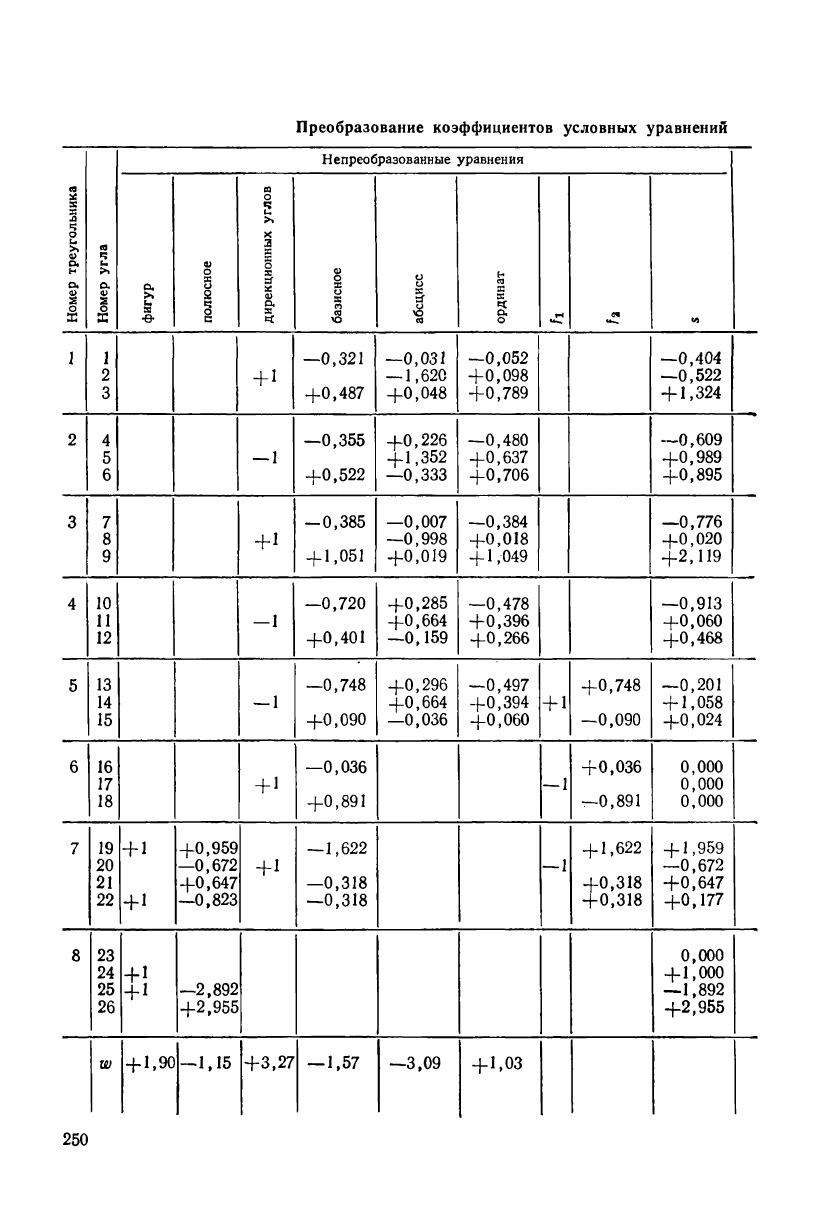
Коэффициенты условных уравнений второй группы и весовых

функций выписывают в сводную табл. 148. Запись углов ведется

по треугольникам. В таблицу включают все треугольники, к углам

которых находятся поправки из уравнений второй группы, причем

независимо от того, ко всем углам треугольника или только к их

части ищутся поправки из уравнений второй группы (см., напри-

мер, треугольник 8 в табл. 148, где есть угол 23, который не вхо-

дит в уравнения второй группы). В табл. 148 ни один из углов не

должен повторяться. В нижней строке этой таблицы записывают

свободные члены условных уравнений. Поскольку свободные чле-

ны вычислены по углам, исправленным первичными поправками,

то они не подвергаются преобразованию.

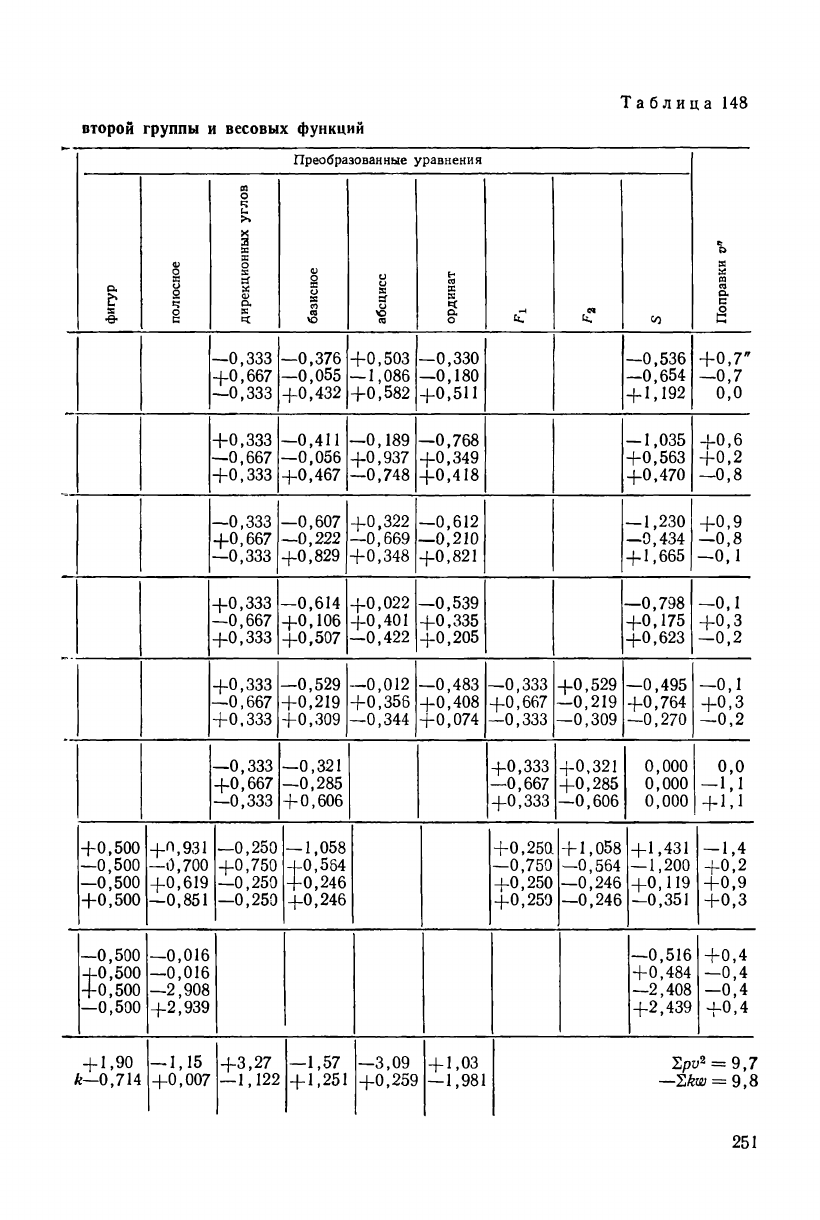
Преобразование коэффициентов условных уравнений второй

группы выполнено во второй части табл. 148. В каждом треуголь-

нике преобразованный коэффициент вычисляется как разность:

Таблица 149

Коэффициенты нормальных уравнений второй группы

3

+

со

Л

§

О.

тН

сл

со

ТА

цэ

«0

»н

<м

0

00

&

2,000 —2,843 -0,500

—0,811

0,000 0,000

0,500

0,811 + 1,90 1*057

1,057

2,000

19,559

—0,700

—1,437

0,000 0,000

0,700

1,437

—1,15

15,566

19,559

4,750

—0,267

—3,449

-1,482

—2,083

-0,060

+3,27

—0,521

4,750

5,005

—0,167

2,783

—0,060

—2,533 —1,57 0,943

0,941

5,005

4,501 0,877

0,356

0,022

—3,09

—0,950

4,501

3,231

0,408 —0,368

+ 1,03

6,479

6,480

3,231

2,083 2,533

6,480

(14.15)

(14.16)

(14.17)

(14.18)

252;

Таблица

150

Решение нормальных уравнений

*1

*2 *5

fi

/2

W

S'

Контроль

2,000

—2,843

—0,500

—0,811

0,000

0,500

0,811

1,90

1,057

—1

1,4215 0,2500

0,4055 0,0000

0,0000

—0,2500 —0,4055

—0,9500

—0,5285 —0,5285

19,559 —0,700

— 1,437

0,000 0,000

0,700

1,437

—1,15

15,566

15,518 —1,411

—2,590

0,000

1,411

2,590

1,551

17,069

—1

0,0909

0,1669

0,0000 0,0000

—0,0909 —0,1669

—0,0999

—1,0999

4,750

—0,267

—3,449

—1,482

—2,083

—0,060

3,27

—0,521

4,497

—0,705

—3,449

— 1,482

— 1,830

0,378

3,886

1,295

— 1

0,1568

0,7670

0,3296

0,4069

—0,0841

—0,8641

—0,2880

—0,2879

5,005

—0,167

2,783

—0,060

—2,533

-1,57

0,943

4,133

—0,708

2,551 0,091

—1,713

0,069

4,423

— 1

0,1713

—0,6172

—0,0220

0,4145

—0,0167

—1,0702

—1,0701

4,501

0,877

0,356

0,022

—3,09

—0,950

1,734

0,177

—1,032

0,018

—0,098

0,801

0,799

—1

—0,1021

0,5952

—0,0104

0,0565

—0,4619

—0,4608

3,231

0,408

—0,368

1,03

6,479

1,150

—0,146

0,812

2,278 4,094

4,094

—I

0,1270 —0,7061

— 1,9809

—3,5600

2,083

2,533

— 1,9809

1

р—=

0,450 0,456

*2

*з

—0,9500

0,0000

+0,5072

—0,2806

+0,0097

—0,0999

0,0000

+0,2087

—0,1020

—0,8641

—0,6529

+0,1984

+0,1961

—0,0167

+

1,2226

+0,0448

+0,0565

+0,2022

— 1,9809

—0,9500

0,0000

+0,5072

—0,2806

+0,0097

—0,0999

0,0000

+0,2087

—0,1020

—0,8641

—0,6529

+0,1984

+0,1961

—0,0167

+

1,2226

+0,0448

+0,2587

—0,9500

0,0000

+0,5072

—0,2806

+0,0097

—0,0999

0,0000

+0,2087

—0,1020

—0,8641

—0,6529

+0,1984

+0,1961

+

1,2507

+0,2587

—0,9500

0,0000

+0,5072

—0,2806

+0,0097

—0,0999

0,0000

+0,2087

—0,1020

—1,1225

+

1,2507

—0,9500

0,0000

+0,5072

—0,2806

+0,0097

+0,0068

—1,1225

— 0,7137

+0,0068

непреобразованный коэффициент минус среднее из суммы непреоб-

разованных коэффициентов в треугольнике (включая и нулевые

коэффициенты при углах данного треугольника).

Сумма преобразованных коэффициентов в каждом треугольни-

ке должна быть равна нулю (как сумма отклонений от среднего).

Сумма 5 преобразованных коэффициентов в строке должна рав-

няться преобразованной сумме s, значение которой вычисляется

таким же образом, как и значения преобразованных коэффициен-

тов при поправках каждого угла в треугольнике.

Проконтролировав правильность значений преобразованных ко-

эффициентов условных уравнений, переходят к вычислению коэф-

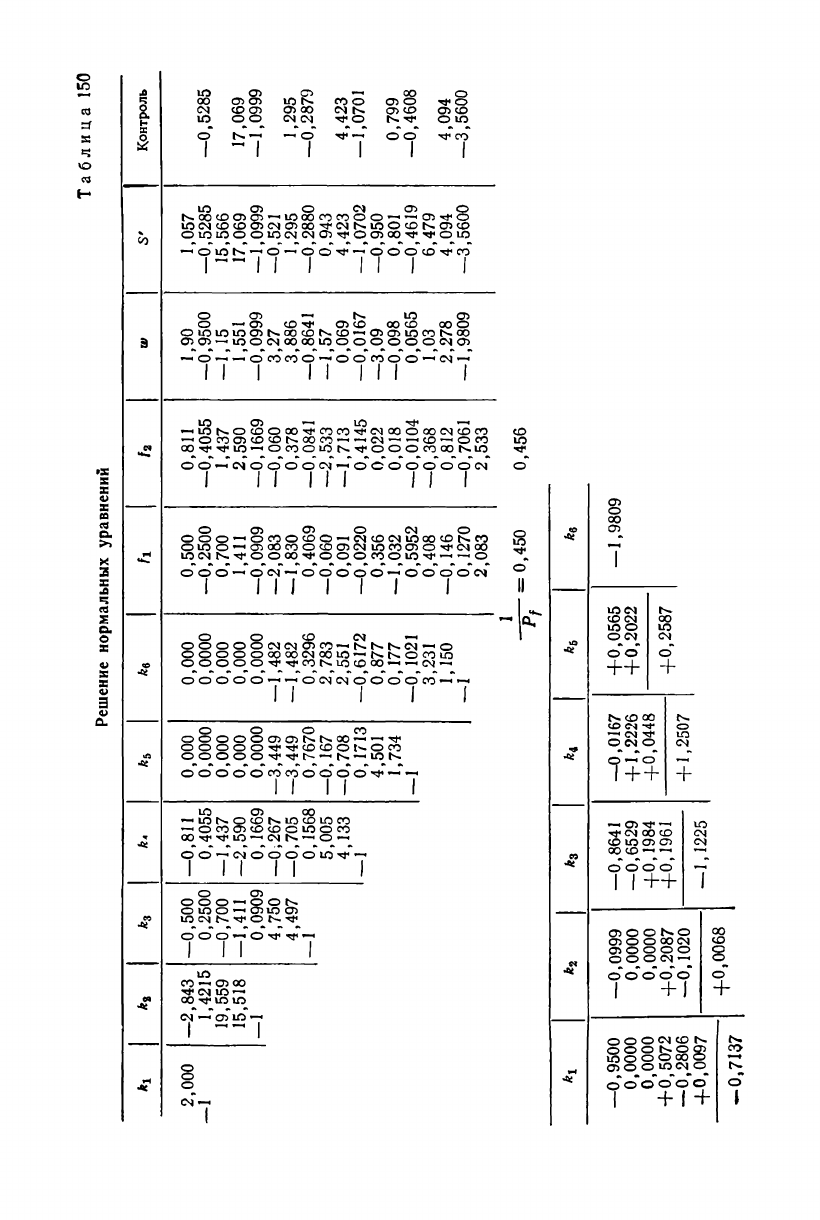
фициентов нормальных уравнений коррелат (табл. 149). Решение

нормальных уравнений выполнено в табл. 150.

Полученные значения коррелат записывают в нижнюю строку

табл. 148 и, используя их, вычисляют по формуле (14.3) вторич-

ные поправки v" в измеренные углы (см. последнюю графу

табл. 148). Сумма поправок v" в каждом треугольнике должна

быть равна нулю.

§ 82. Окончательные вычисления элементов сети

и оценка их точности

Взяв из табл. 144 первичные поправки v\ а из табл. 148 —

вторичные поправки и", вычисляют для каждого измеренного угла

общие поправки v = v' + v"

t

с учетом которых находят значения

уравненных углов. Сумма уравненных углов в каждом треуголь-

нике должна быть равна 180°. С уравненными углами решают

треугольники и получают длины уравненных сторон. Для нашей

сети эти вычисления выполнены в табл. 151.

Используя уравненные углы и стороны, вычисляют прираще-

ния координат и окончательные координаты всех пунктов. Вычис-

ления выполняют по известной нам схеме, см., например, табл.65.

В данном случае ограничимся приведением только лишь каталога

•окончательных значений координат с указанием некоторых длин

и дирекционных углов сторон (табл. 152).

Контролем правильности уравнительных вычислений является

удовлетворение всех условных уравнений, возникающих в сети, и

как следствие сходимость значений координат, вычисляемых в

каждом треугольнике по двум его сторонам.

Оценка точности уравненных элементов сети

Среднюю квадратическую ошибку единицы веса найдем по

формуле

ц

= /(WV}.

В нашей сети 2pv

2

—19,90 (см. табл. 151), число избыточных из-

мерений равно числу всех условных уравнений г = 14. С этими дан-

ными получим |л=1,2".

254;

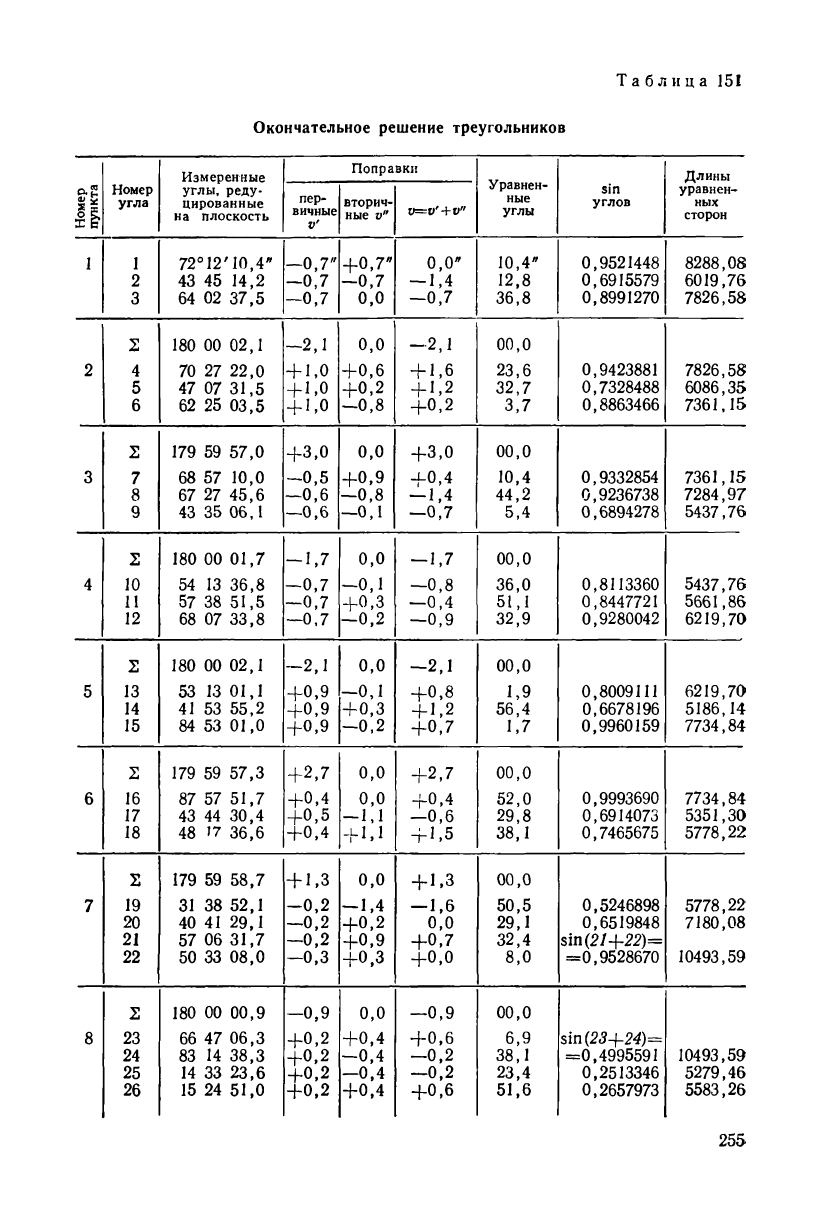
Таблица 187

Окончательное решение треугольников

Измеренные

Поправки

Уравнен-

ные

углы

Длины

Номер

пункта

Номер

угла

углы, реду-

цированные

на

плоскость

пер-

вичные

V'

вторич-

ные V"

v=v'+v"

Уравнен-

ные

углы

sin

углов

уравнен-

ных

сторон

1 1

2

3

72°12'10,4"

43 45 14,2

64 02 37,5

—0,7"

—0,7

+0,7"

—0,7

0,0

0,0"

— 1,4

-0,7

10,4"

12,8

36,8

0,9521448

0,6915579

0,8991270

8288,08

6019,76

7826,58

2

180 00 02,1

—2,1

0,0

-2,1

00,0

2

4

5

6

70 27 22,0

47 07 31,5

62 25 03,5

+ 1,0

+1,0

+0,6

+0,2

-0,8

+ 1,6

+ 1,2

+0,2

23.6

32.7

3,7

0,9423881

0,7328488

0,8863466

7826,58

6086,35

7361,15

2

179 59 57,0

+3,0 0,0 +3,0

00,0

3

7

8

9

68 57 10,0

67 27 45,6

43 35 06,1

—0,5

—0,6

+0,9

-0,8

—0,1

+0,4

— 1,4

—0,7

10,4

44,2

5,4

0,9332854

0,9236738

0,6894278

7361,15

7284,97

5437,76

2

180 00 01,7

— 1,7

0,0

— 1,7

00,0

4

10

11

12

54 13 36,8

57 38 51,5

68 07 33,8

—0,7

-0,1

+0,3

-0,2

—0,8

—0,4

—0,9

36.0

51.1

32,9

0,8113360

0,8447721

0,9280042

5437,76

5661,86

6219,70

2

180 00 02,1

—2,1

0,0

—2,1

00,0

5

13

14

15

53 13 01,1

41 53 55,2

84 53 01,0

+0,9

-0,1

+0,3

-0,2

+0,8

+ 1,2

+0,7

1,9

56,4

1,7

0,8009111

0,6678196

0,9960159

6219,70

5186,14

7734,84

2

179 59 57,3

+2,7

0,0

+2,7

00,0

6

16

17

18

87 57 51,7

43 44 30,4

48 17 36,6

+0,4

+0,5

+0,4

0,0

—1,1

+ U

+0,4

—0,6

+ 1,5

52.0

29,8

38.1

0,9993690

0,6914073

0,7465675

7734,84

5351,30

5778,22

2

179 59 58,7

+ 1,3

0,0

+ 1,3

00,0

7

19

20

21

22

31 38 52,1

40 41 29,1

57 06 31,7

50 33 08,0

—0,2

-0,3

-1,4

+0,2

+0,9

+о,з

— 1,6

0,0

+0,7

+0,0

50,5

29,1

32,4

8,0

0,5246898

0,6519848

sin

(21+22)=

=0,9528670

5778,22

7180,08

10493,59

2

180 00 00,9

—0,9

0,0

—0,9

00,0

8

23

24

25

26

66 47 06,3

83 14 38,3

14 33 23,6

15 24 51,0

+0,2

+0,4

-0,4

—0,4

+0,4

+0,6

-0,2

+0,6

6,9

38,1

23,4

51,6

sin

(23+24)=

=0,4995591

0,2513346

0,2657973

10493,59

5279,46

5583,26

255

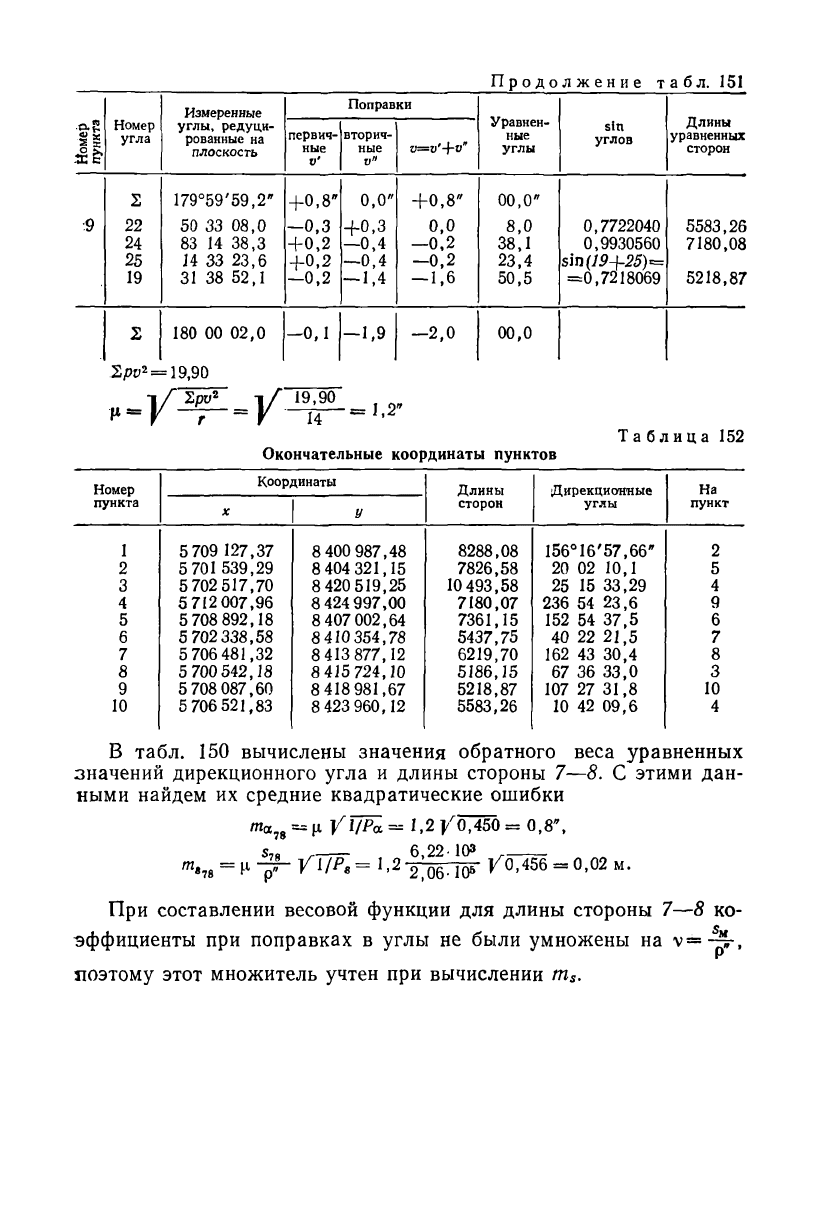
Продолжение табл. 151

Измеренные

Поправки

Уравнен-

ные

углы

Длины

уравненных

сторон

Номер

пункта

Номер

угла

углы, редуци-

рованные на

плоскость

первич-

ные

V'

вторич-

ные

V

м

Уравнен-

ные

углы

sin

углов

Длины

уравненных

сторон

2

179°59'59,2"

+0,8"

0,0"

+0,8"

00,0"

•9

22

24

25

19

50 33 08,0

83 14 38,3

14 33 23,6

31 38 52,1

—0,3

+0,2

—0,2

+0,3

-0,4

—0,4

— 1,4

0,0

-0,2

-1,6

8,0

38,1

23.4

50.5

0,7722040

0,9930560

sin (19+25)-=

=0,7218069

5583,26

7180,08

5218,87

2

180 00 02,0 |

—0,1

-1,9

—2,0

00,0

.2^ =

19,90

Таблица 152

Окончательные координаты пунктов

Номер

Координаты

Длины

Дирекционные

На

пункта

X

У

сторон

углы

пункт

1

5 709 127,37 8 400 987,48

8288,08 156°16'57,66"

2

5 701 539,29 8 404 321,15 7826,58

20 02 10,1 5

3

5 702 517,70 8 420 519,25

10 493,58

25 15 33,29

4

5 712 007,96

8 424 997,00

7180,07

236 54 23,6

9

5

5 708 892,18

8 407 002,64 7361,15

152 54 37,5 6

6 5 702338,58

8410354,78

5437,75

40 22 21,5 7

7

5 706 481,32

8 413 877,12

6219,70

162 43 30,4

8

5 700 542,18

8 415 724,10 5186,15

67 36 33,0

3

9

5 708 087,60

8 418 981,67 5218,87

107 27 31,8

10

10 5 706 521,83

8 423 960,12

5583,26

10 42 09,6

4

В табл. 150 вычислены значения обратного веса уравненных

значений дирекционного угла и длины стороны 7—8. С этими дан-

ными найдем их средние квадратические ошибки

V ЦРа —1,2 |/

а

0~450 = 0,8",

s

7fi г

6,22 10

3

= = 1.2

2 Q6

,

1Q

6 КО,456 = 0,02 м.

При составлении весовой функции для длины стороны 7—8 ко-

эффициенты при поправках в углы не были умножены на v

—

поэтому этот множитель учтен при вычислении m

s

.

Часть V

РЕШЕНИЕ ЗАДАЧ

СФЕРОИДИЧЕСКОЙ ГЕОДЕЗИИ

Глава 15

ВЫЧИСЛЕНИЕ ДЛИН ЛИНИЙ И ПЛОЩАДЕЙ

НА ПОВЕРХНОСТИ ЭЛЛИПСОИДА

§ 83. Вычисление длин дуг меридианов и параллелей

Длина дуги меридиана S

M

между точками с широтами В\ и

определяется из решения эллиптического интеграла вида

р

5

М

=\ЛШ, (15.1)

Bi

который, как известно, не берется в элементарных функциях. Для

решения интеграла используют два способа:

1. Раскладывают подынтегральное выражение в степенной ряд

и, ограничиваясь некоторым числом членов ряда, выполняют за-

тем почленное интегрирование, которое, таким образом, сводится

к интегрированию в элементарных функциях.

2. Применяют численное интегрирование методами, известны-

ми в вычислительной математике.

Второй способ в настоящее время является более точным и

удобным. В соответствии с этим способом численное интегрирова-

ние можно выполнить, например, по формуле Симпсона

В

»

5

М

» j

MdB

=

(B2

^/

l)

(M

l

+

4M

c

p

+ M

2

), (15.2)

Bi

где

а(1 — е

2

)

0

1 -f 0

t

25e

2

sin

2

£f

M

'

=

(lJ»sm-ад'/,

=а(1

~

е)

• (

,5

-

3

>

где В и В

2

— широты концов дуги меридиана; М

и

М

2

> М

СР

—зна-

чения радиусов кривизны меридиана в точках с широтами В

ь

В

2

и 5

С

р= 7бр"=8 080 228-10"

13

.

Для контроля вычислений длину дуги меридиана S

M

следует

вычислить как сумму дуг Я\ и Х

2

меридиана от точки с широтой

17—2296 257

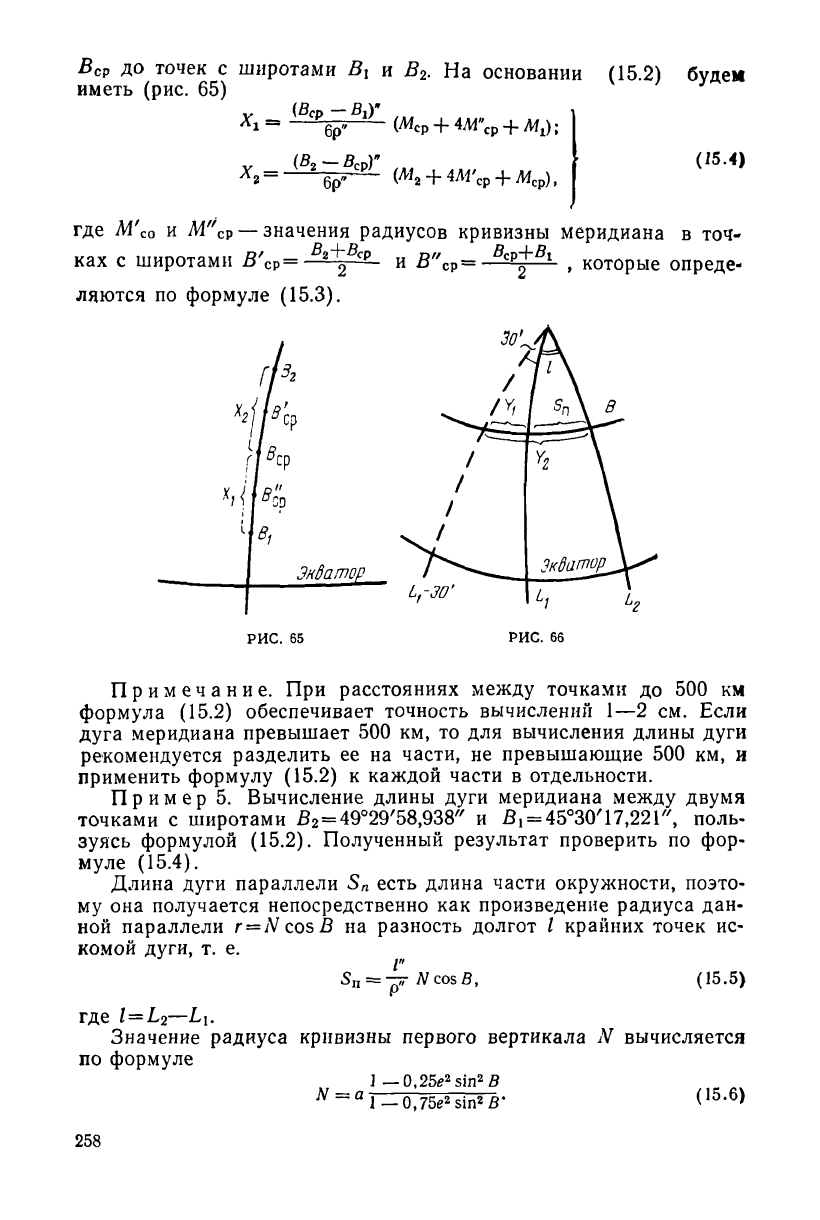
Вер до точек с широтами В

х

и В

2

. На основании (15.2) будем

иметь (рис. 65)

(В

С

п — в

г

у

Х

1

а

^Р +

4Л

*"ср + м

г

);

(В

2

— Д

ср

)

(15.4)

где ЛГ

С0

и М"ср — значения радиусов кривизны меридиана в точ-

ках с широтами В'

ср

=

и

Д^

СРАА

^CP+^I ^

которые

опреде-

ляются по формуле (15.3).

РИС. 65

РИС. 66

Примечание. При расстояниях между точками до 500 км

формула (15.2) обеспечивает точность вычислений 1—2 см. Если

дуга меридиана превышает 500 км, то для вычисления длины дуги

рекомендуется разделить ее на части, не превышающие 500 км, и

применить формулу (15.2) к каждой части в отдельности.

Пример 5. Вычисление длины дуги меридиана между двумя

точками с широтами В

2

=49

0

29'58,938" и В

1

= 45°30

/

17,221

//

, поль-

зуясь формулой (15.2). Полученный результат проверить по фор-

муле (15.4).

Длина дуги параллели S

n

есть длина части окружности, поэто-

му она получается непосредственно как произведение радиуса дан-

ной параллели r =

jV

cos В на разность долгот I крайних точек ис-

комой дуги, т. е.

Г

= Ncos В, (15.5)

где /=L

2

—L

b

Значение радиуса кривизны первого вертикала N вычисляется

по формуле

1 —0,25*2 sin

2

В

N \ — 0,75е

2

sin

2

В* (

15

'

6

>

258;

Яковлев Н.В. и др. Практикум по высшей геодезии. Вычислительные работы

Подождите немного. Документ загружается.