Яковлев Н.В. и др. Практикум по высшей геодезии. Вычислительные работы

Подождите немного. Документ загружается.

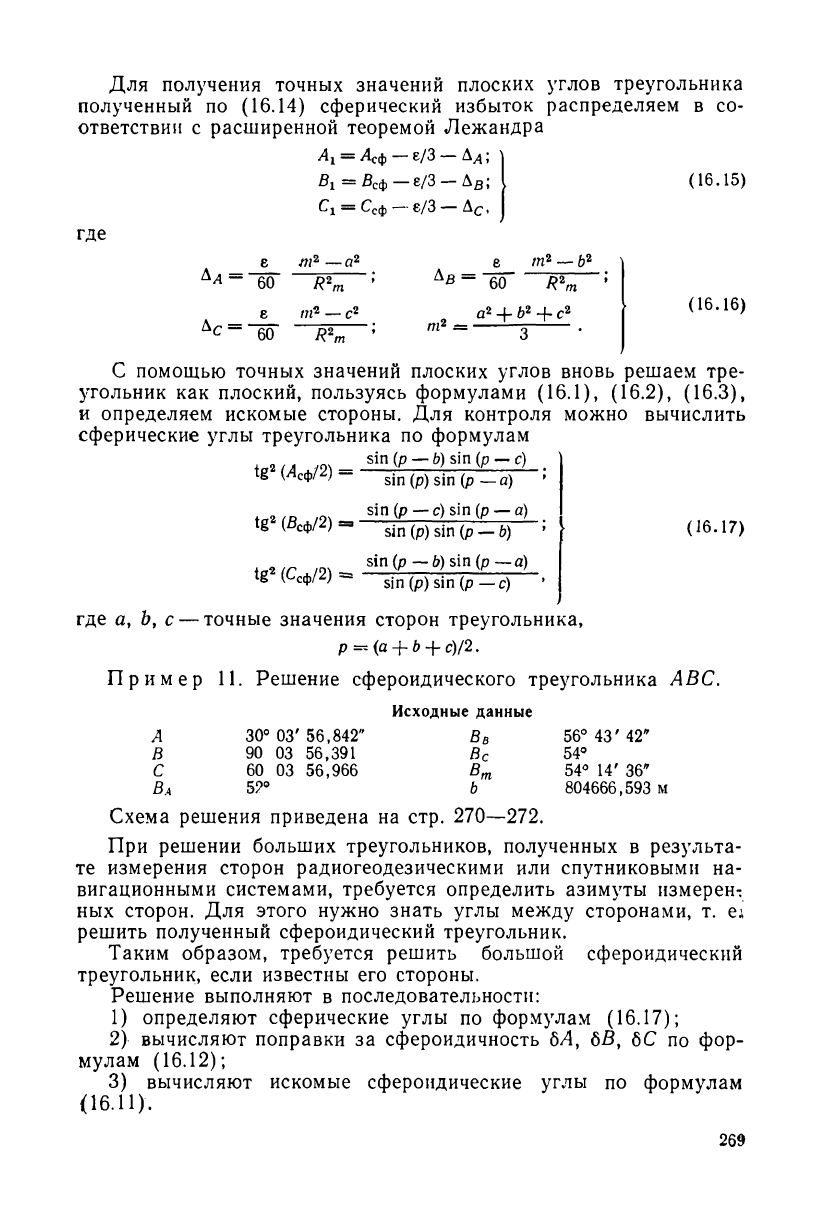
Для получения точных значений плоских углов треугольника

полученный по (16.14) сферический избыток распределяем в со-

ответствии с расширенной теоремой Лежандра

Лсф —

е/3 — ;

= В

ф —е/3 — Ад;

ф —

е/3 — Ас,

(16.15)

где

е т*—а* е т

—

]

60 Я

•

В= 60 '

е т-

—

а» + 6«+

(16.16)

60 R*

т2

- 3

С помощью точных значений плоских углов вновь решаем тре-

угольник как плоский, пользуясь формулами (16.1), (16.2), (16.3),

и определяем искомые стороны. Для контроля можно вычислить

сферические углы треугольника по формулам

te« (А

*/2)

= sin(p-c)

tg Исф/^ sin (р) sin (р — а)

(Дсф/2)'

sin (р

— с)

sin (р — а)

sin (р) sin

(р

—

Ь)

Ig И-сф/^ - Sin (Р) sin (р—с)

(16.17)

где а, Ь, с-

В.4

Дс

Лт

56° 43' 42"

54°

54° 14' 36"

804666,593 м

•точные значения сторон треугольника,

р = (а +

+ с)/2.

Пример 11. Решение сфероидического треугольника ЛВС.

Исходные данные

30° 03' 56,842"

90 03 56,391

60 03 56,966

5?° Ь

Схема решения приведена на стр. 270—272.

При решении больших треугольников, полученных в результа-

те измерения сторон радиогеодезическими или спутниковыми на-

вигационными системами, требуется определить азимуты измерен-

ных сторон. Для этого нужно знать углы между сторонами, т. е;

решить полученный сфероидический треугольник.

Таким образом, требуется решить большой сфероидический

треугольник, если известны его стороны.

Решение выполняют в последовательности:

1) определяют сферические углы по формулам (16.17);

2) вычисляют поправки за сфероидичность 6/4, б В,

б С

по фор-

мулам (16.12);

3) вычисляют искомые сфероидические углы по формулам

(16.11).

269;

Схема решения

1. Вычисление поправок 6Л, 6В, б С в углы

за сфероидичность треугольника

Формулы

Результаты

вычислений

Формулы

Результаты

вычислений

а (большая полуось эл-

липсоида Красовского)

а(

1—е2)

Вс

Вт

0,25е

1,25е

sin В А

sin В в

sin В

sin

В в

sin

Вт

0,25е

sin

0,25е

sin

0,25е

sin

0,25<?

sin

1,25е

sin

В*

1,25<?

sin

1,25е

sin

1,25е

sin

Вт

+0,25е

sin

1+0,25е

sin

1+0,25е

sin

1+0,25е

sin

1—l,25e

sin

1—1,25е

sin

6378 245 м

6 335 553 м

52°00'00"

56 43 42

54 00 00

54 14 36

0,00167

0,00837

0,78801

0,83608

0,80902

0,81151

0,62096

0,69903

0,65451

0,65855

0,00104

0,00117

0,00109

0,00110

0,00520

0,00585

0,00548

0,00551

1,00104

1,00117

1.00109

1.00110

0,99480

0,99415

1—l,25e

sin

1—1,25^ sin

0,75е

sin

0,75е

sin

0,75е

sin

0,75е

sin

1—0,25^ sin

В,,

—0,25е

sin

1—0,25e

sin

1—0,25е

sin

1—0,75е

sin

В а

1— 0,75е

sin

1—0,75е

sin

Вс

1— 0,75<?

sin

Вт

e/12

(K^I—/С)

/К

(Кв-К)1К

(Kc-K)IK

б л

6В

6С

0,99452

0,99449

6 375 293 м

6 380 290 м

6 377 406 м

6 377 662 м

0,00502

0,00312

0,00351

0,00329

0,00331

0,99896

0,99883

0,99891

0,99890

0,99688

0,99649

0,99671

0,99669

391

553 м

6 393 222 м

6 392 323 м

6 392 387 м

59,074"

0,00050

—0,00054

0,00005

0,030"

—0,032

0,003

2. Вычисление сферических углов

ЛСФ=Л—6Л

Всф —В—б В

30°03'56,812'

90 03 56,423

Ссф = С—6 с

03'56,963*

3. Вычисление приближенного значения сферического избытка

sin

sinC

sin

sin С

0,002530

647 488,320

0,50099395

0,86659924

0,43416097

sin

sinC

sin В

D i

e°

281 111,415

0,99999934

281 111,61

711,212"

1Г51,212

270;

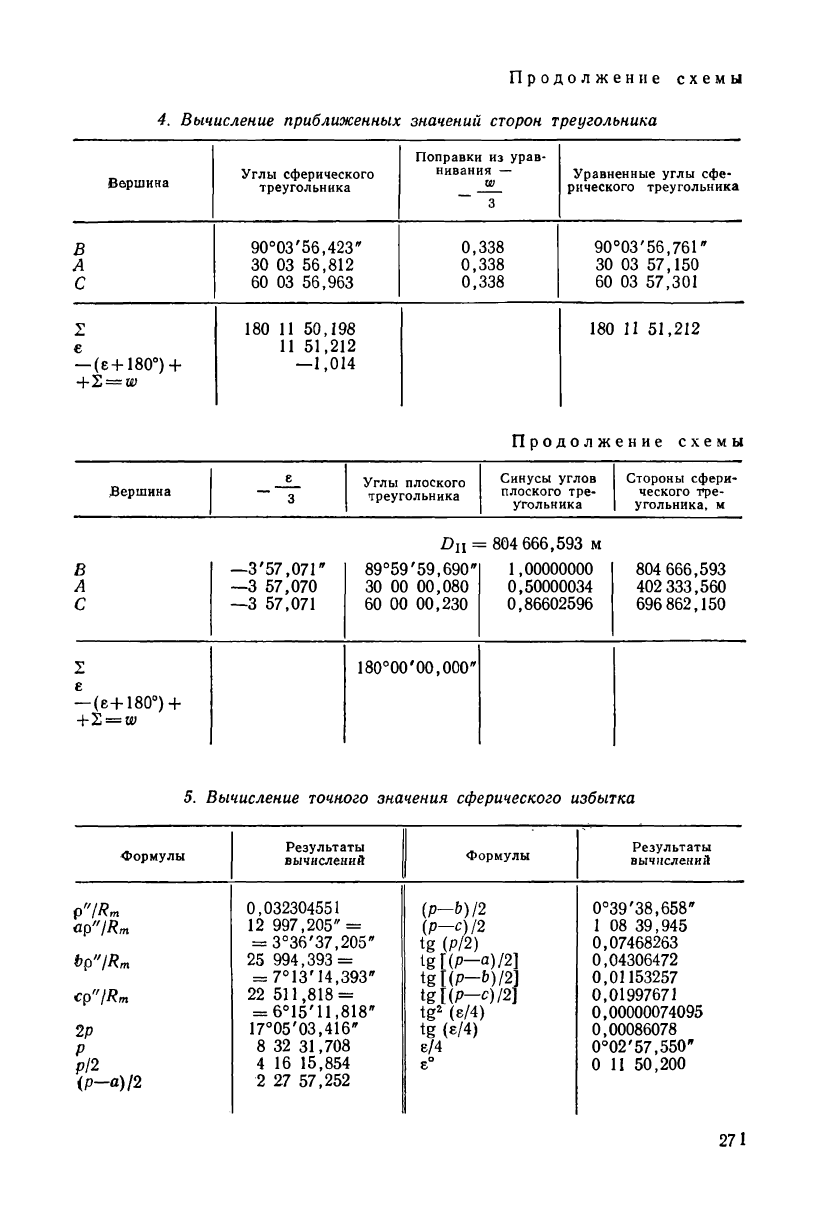
Продолжение схемы

4. Вычисление приближенных значений сторон треугольника

Вершина

Углы сферического

треугольника

Поправки из урав-

нивания —

~ 3

Уравненные углы сфе-

рического треугольника

90°03'56,423"

0,338

90°03'56,761"

30 03 56,812

0,338

30 03 57,150

60 03 56,963

0,338 60 03 57,301

— (e-f 180°) +

= ш

180 11 50,198

11 51,212

—1,014

180 11 51,212

Продолжение схемы

Зершнна

~ 3

Углы плоского

треугольника

Синусы углов

плоского тре-

угольника

Стороны сфери-

ческого тре-

угольника, м

= 804 666,593 м

—3'57,071" 89°59'59,690" 1,00000000

804 666,593

—3 57,070

30 00 00,080

0,50000034

402 333,560

—3 57,071

60 00 00,230

0,86602596

696 862,150

—

(е-Н80°) +

+ 2 = w

180°00'00,000"

5. Вычисление точного значения сферического избытка

Формулы

Результаты

вычислений

Формулы

Результаты

вычислений

p'Vtfm

0,032304551

(p-

-6)/2

0°39'38,658"

ap"/R

12 997,205" =

(p-

-c)l 2

1 08 39,945

ap"/R

= 3°36'37,205"

tg (Pi2)

0,07468263

bp"/Rm

25 994,393 =

tgl

[(p—a)/2]

0,04306472

bp"/Rm

= 7°13

14,393"

[(P~b)l2] 0,01153257

Cp"jR

22 511,818 =

tgl

l(P-c)I2]

0,01997671

Cp"jR

= 6°15'11,818"

17°05'03,416"

(8/4)

0,00000074095

2 p

= 6°15'11,818"

17°05'03,416" tg (г/4)

0,00086078

8 32 31,708

e/4

0°02

57,550'

p/2

4 16 15,854

0 11 50,200

(p-a)/2

2 27 57,252

271

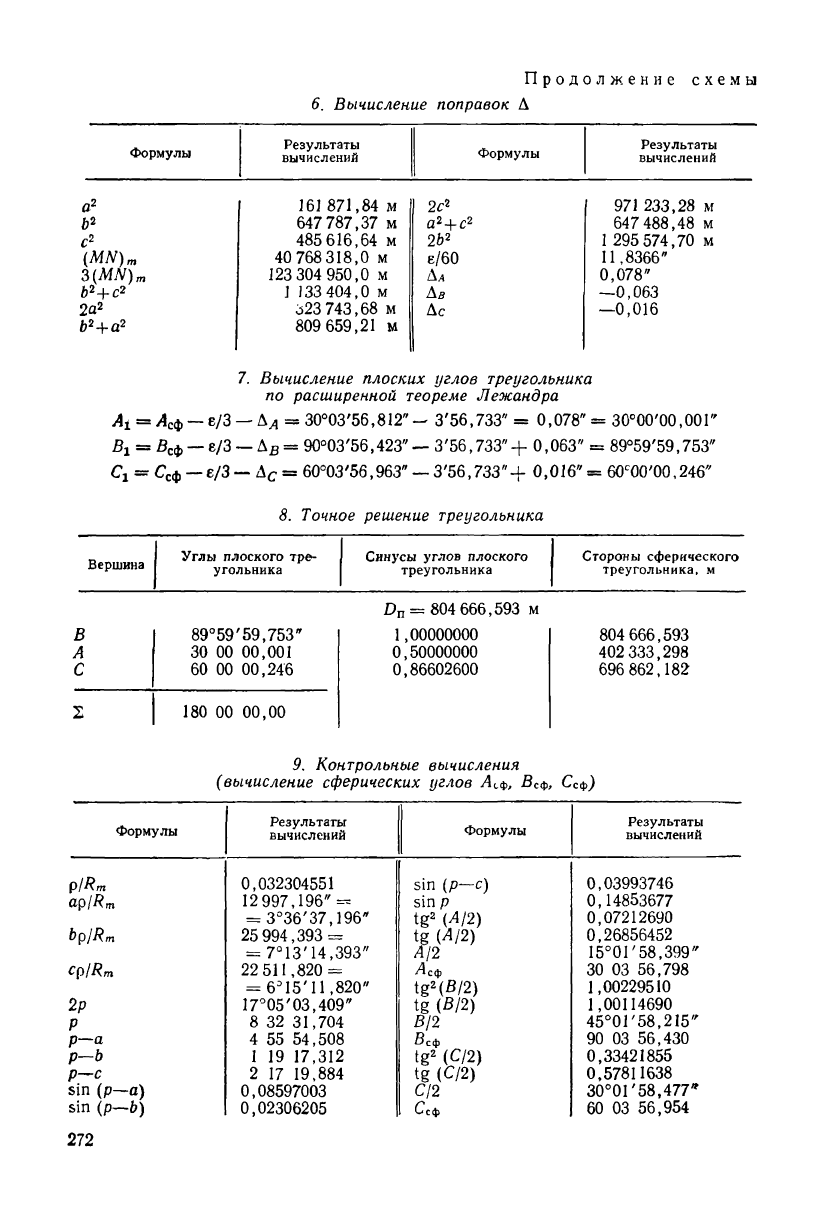
Продолжение схемы

6. Вычисление поправок Д

Формулы

Результаты

вычислений

Формулы

Результаты

вычислений

а'

с'

(MN)

3 (MN)

-he

2а

+а

161 871,84 м

2с

971 233,28 м

647 787,37 м а

+с

647 488,48 м

485 616,64 м

2 Ь

1 295 574,70 м

40 768318,0 м

е/60

11,8366"

123 304 950,0 м

Дл

0,078"

1 133 404,0 м

Д*

—0,063

523 743,68 м

Дс

—0,016

809 659,21 м

—0,016

7. Вычисление плоских углов треугольника

по расширенной теореме Лежандра

= Л

ф — е/3 — Ал 30°03'56,812"

—

3'56,733" = 0,078" = 30°00'00,001"

= В

ф — е/3 — Д

= 90°03'56,423" — 3'56,733" + 0,063" = 89°59'59,753"

С г - Ссф — е/3 — Дс = 60°03'56,963" — 3'56,7330,016" = 60

00'00,246"

8. Точное решение треугольника

Вершина

Углы плоского тре-

угольника

Синусы углов

ПЛОСКОГО

треугольника

Стороны сферического

треугольника, м

= 804 666,593 м

89°59'59,753"

30 00 00,001

60 00 00,246

1,00000000

0,50000000

0,86602600

804 666,593

402 333,298

696 862,182

180 00 00,00

9. Контрольные вычисления

(вычисление сферических углов Л

Ф, В

Ф, ССФ)

Формулы

Результаты

вычислений

Формулы

Результаты

вычислений

р !Rm

0,032304551

sin (p—c)

0,03993746

apIRm

12 997,196"

—

sin p

0,14853677

apIRm

= 3°36'37,196"

(A 12)

0,07212690

bpjRm

25 994,393 =

tg (A/2)

0,26856452

bpjRm

= 7°13'14,393"

A12

15°0Г 58,399"

Cp/Rm

22 511,820

—

А сф

30 03 56,798

Cp/Rm

= 6

15' 11,820" tg

(B/2)

1,00229510

17°05'03,409"

tg (S/2)

1,00114690

8 32 31,704

5/2

45°0Г58,215"

p—a

4 55 54,508

90 03 56,430

p-b

1 19 17,312

(CI2)

0,33421855

P—C

2 17 19,884

tg (C/2)

0,57811638

sin (p—a)

0,08597003

С12

30°01'58,477*

sin (p—b)

0,02306205

Ссф

60 03 56,954

272;

Контрольные вычисления можно выполнить по следующей схе-

ме: 1) определить поправки Д по формулам (16.16);

2)) определить сферический избыток треугольника по формуле

(16.14);

3) вычислить сферические углы треугольника на основании

расширенной теоремы Лежандра по формулам (16.15);

4) вычислить поправки б Л, б В и б С за сфероидичность по фор-

мулам (16Л2);

5) вычислить сфероидические углы Л, В

С по формулам.

(i6.li).

Глава 17

РЕШЕНИЕ ПРЯМОЙ И ОБРАТНОЙ

ГЕОДЕЗИЧЕСКИХ ЗАДАЧ

§ 87. Общие сведения по решению прямой и обратной

геодезических задач

Определение координат некоторой точки по известным коор-

динатам других точек и измеренным или заданным угловым и ли-

нейным величинам называется главной геодезической задачей.

Такая задача может быть поставлена в различных координат-

ных системах. В высшей геодезии принято решать эту задачу в

геодезической системе координат,

которая предполагает известными

размеры и ориентировку конкретно-

го референц-эллипсоида. В геодези-

ческой практике СССР для этих це-

лей используется референц-эллип-

соид Красовского.

Если на поверхности референц-

эллипсоида выбрать две произволь-

ные точки Q1 и Q

, ТО кратчайшее

расстояние между ними S называет-

ся геодезической линией. Если при

этом точку Q1 назвать начальной, а

— конечной, то направление QIQ

называется прямым направлением

н Л12•— прямым азимутом этого направления, а направление

Q2Q1 — обратным направлением и Л

\ — обратным азимутом

(рис. 69).

Главную геодезическую задачу принято рассматривать в виде-

двух задач: прямой и обратной.

Прямая геодезическая задача состоит в том, чтобы по извест-

ным координатам начальной точки Ви L\, прямому азимуту A

и расстоянию S между точками Qi и Q

определить координаты,

конечной точки В

2у

и обратный азимут Л

1 (см. рис. 69).

Обратная геодезическая задача заключается в том, чтобы по.

РИС. 69

18—2296

273;

координатам начальной и конечной точек В

2у

определить

расстояние S между ними и азимуты Л

и Л21 (см. рис. 69).

В геодезической практике прямую и обратную геодезические

задачи приходится решать для различных длин геодезических ли-

ний. На практике установилась определенная градация возмож-

ных расстояний, для каждой из которых существует наиболее

удобный метод решения главных геодезических задач.

Малые расстояния (от 20 до

200 км) встречаются при вычисле-

нии сторон треугольников и замы-

кающих звеньев триангуляции

1 класса.

Средние расстояния (от 200 до

800 км) имеют место при вычисле-

нии диагоналей полигонов триангу-

ляции 1 класса, при обработке аст-

рономо-геодезической сети, при раз-

витии динамической (ракетной)

триангуляции, радиогеодезических

сетей и других задач.

Большие расстояния (более

800 км) встречаются при ориенти-

ровке референц-эллипсоида, при

геодезическом соединении матери-

ков методом космической триангу-

ляции, в радионавигации, при уста-

новлении единой координатной си-

стемы, в целях слежения за управ-

ляемыми ракетами и т. д.

Для решения главных геодезических задач необходимо уста-

новить уравнения связи исходных и определяемых величин. Наи-

более простой и естественный способ установления таких урав-

нений связи и в конечном итоге решения главных геодезических

задач заключается в непосредственном решении треугольника

Q\PQz (см. рис. 69), в котором исходные данные и определяемые

неизвестные как в прямой, так и в обратной задачах являются

элементами этого треугольника. Например, в случае прямой гео-

дезической задачи исходными данными являются стороны 5, QiP

и угол Л12. Из решения треугольника получаются другие его эле-

менты /, р, Q

P, С ПОМОЩЬЮ которых определяются искомые ве-

личины:

= L

+ l; = 90° -Q

L; Л

= 360°-р.

Такой путь решения главных геодезических задач называется

прямым. Однако в связи с большими сторонами полярного тре-

угольника Q1PQ2, достигающими нескольких тысяч километров,

его нужно рассматривать как сфероидический. Это обстоятельство

значительно усложняет решение и требует использования 10-знач-

ных таблиц тригонометрических функций. Поэтому применяют

другой путь решения, который называют косвенным.

274;

Косвенный путь решения главных геодезических задач заклю-

чается в определении разностей широт, долгот и азимутов, на ос-

новании уравнений связи этих величин с исходными данными. На-

пример, для прямой задачи определяют

dB*=B

— B

= q>

, L

, S);

, Л

, S);

dA = A

—

, L

, S)

и затем B

= B

+ dB\ l

= L

+ dL; Л

= Л

± 180° + dA.

(17.1)

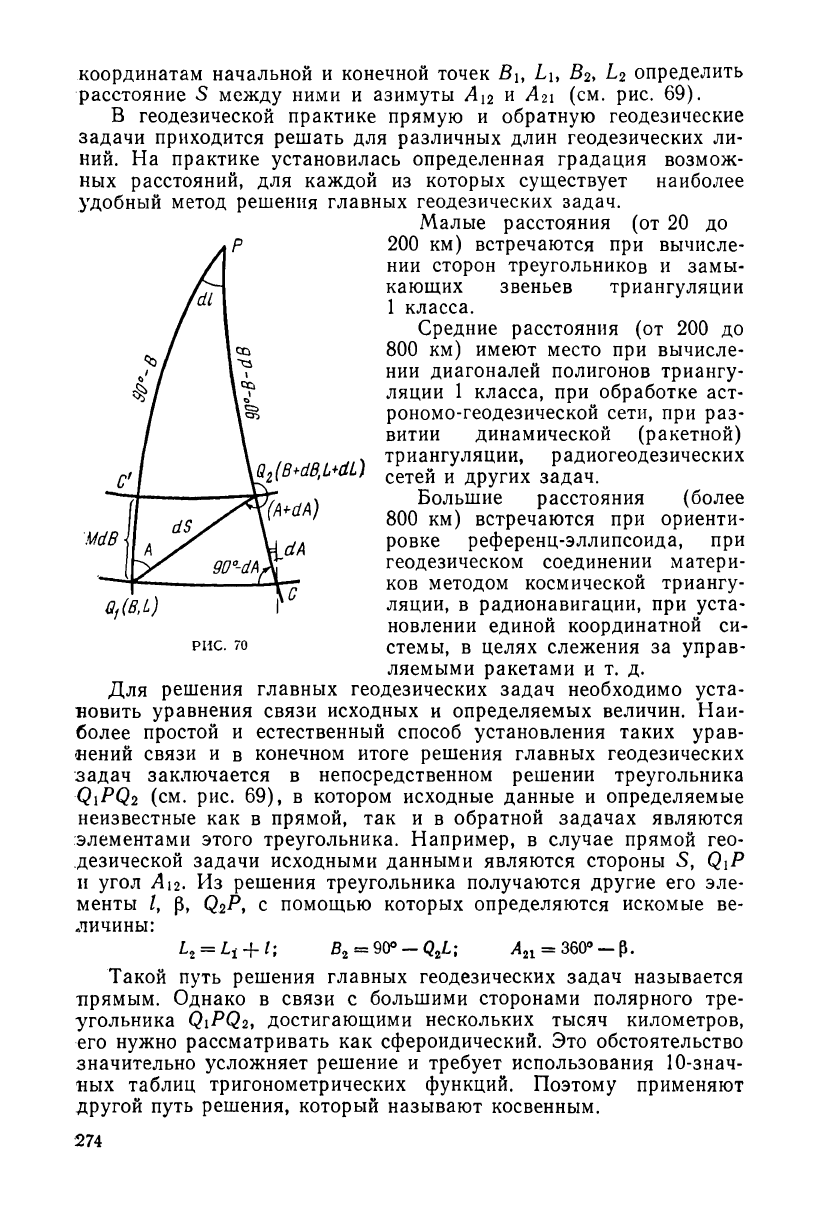
Вид уравнений связи (17.1) устанавливают следующим образом.

На основании рис. 70, где Qi и Q

— две бесконечно близкие точ-

ки на эллипсоиде, dS — отрезок геодезической линии, QiC и

Q2C'—бесконечно малые дуги параллелей, из треугольника

QiC'Q

имеем

MdB

=г

cos

Л,

или rdL = N cos BdL^dS sin А, (17.2)

где г — радиус параллели.

Из равнобедренного сферического треугольника Q\PC, имея в

виду, что РС=(90°—В)

и пользуясь мнемоническим правилом ре-

шения сферических треугольников, получим

cos (90°

— В)

= ctg dL ctg (90°

—

dA) \

tg dL sin В = tg dA;

dA = dLswB; (17-3)

dS sin

tgB

dA =

Из (17.2) и (17.3, окончательно получим

•

= -тг-

cos

Л;

c= —yy— sec В = sec В sin Л;

cos Л

sin Л

sin

(17.4)

tg £ sin Л,

где У=1Л + е

cos

В — вторая функция геодезической широты;

С= —радиус кривизны меридиана эллипсоида в полюсах; е„

У 1—е'

е' — первый и второй эксцентриситеты меридианного эллипса.

Выражения (17.4) являются обыкновенными дифференциаль-

ными уравнениями первого порядка. Эти уравнения лежат в ос-

нове практически всех существующих методов решения главных

геодезических задач. Выражения (17.4) дают возможность опре-

делить разности {В

—В1), (L

—L

)

(А

—А\± 180°) путем инте-

грирования (17.4) между двумя точками на эллипсоиде.

276;

После интегрирования получим

с v

—В

= I -рг- cos AdS;

— Lj

= J — sec В

sin

AdS;

(17.5)

sin

В sec В sin

AdS.

Формулы (17.5) непосредственно используются для решения

прямой геодезической задачи. В основе решения обратной геоде-

зической задачи лежат те же формулы.

Практическая реализация выражений (17.5) встречает суще-

ственные трудности, заключающиеся в том, что в общем виде

выражения (17.5) проинтегрировать нельзя, так как переменные

В и А не выражаются в замкнутом виде через независимую пере-

менную S. Кроме того, функции V н С зависят от эксцентрисите-

та е.

Поэтому для решения задачи подынтегральные функции в

(17.5) раскладывают в степенные ряды по степеням 5 для малых

и средних расстояний или по степеням е

для больших расстоя-

ний. В результате разложения, например в ряд Тейлора, будем

иметь:

где индекс внизу скобок указывает на то, что частные производ-

ные берутся в начальной точке, т. е. при B

После подстановки в (17.6) частных производных, первый по-

рядок которых имеет вид (17.4), получаются рабочие формулы в

виде рядов. Полученные формулы допускают некоторые упроще-

ния. В связи с этим появились широко известные методы решения

главных геодезических задач: метод вспомогательной точки и ме-

тод Гаусса, основанный на разложении в ряд по среднему аргу-

менту.

В тех случаях, когда для решения главных геодезических за-

дач применяется разложение в ряд, возникает естественный во-

прос о том, сколько членов ряда нужно использовать для получе-

ния решения. Для ответа на этот вопрос прежде всего необходи-

мо выяснить, какая точность решения требуется. При этом будем

/ dB \ j d*B_\ S

/ d

B \ S

i = \dS /

V dS

)

2! +[ dSз )

3! +

-.(JL\ с / d*L \ S

( d*L \ S

f^+y dS

)

2! +V )

( dA\ ( d

A \ S

( d

A \ S

- A

± 180° = 5 + — + (I — + ''

(17.6)

276;

ориентироваться на самое высокоточное построение, которому со-

ответствует триангуляция 1 класса.

Пусть сторона триангуляции 1 класса S = 20 км, средняя квад-

ратическая ошибка измерения углов /Пр =0,7", относительная

ошибка измерения стороны 1 :400

ООО.

Тогда линейный сдвиг вер-

шины треугольника из-за ошибок углов и расстояний равен

dS = -^г-

= TW

104

= М7 м, dS = 10

)/(4-105)

= 0

,05 м.

Таким образом, можно считать, что в среднем проекция линей-

ного сдвига вершины треугольника на меридиан и параллель со-

ставляет ~0,05 м. В градусной мере эта величина равна

0,05 0,05

0,05

dB « -Jf-

р"

105

002

= 64-10

cos В Р"'

При В = 60° получим dL = 0,003".

Так как координаты в триангуляции передают от пункта к

пункту, то для того, чтобы исключить ошибки вычислений, В и

L нужно вычислять на порядок точнее, т. е. с ошибкой не ниже

0,0002—0,0003".

Уравненные на станции направления в триангуляции 1 класса

определяются с ошибкой 0,01", поэтому вычислять их нужно с

ошибкой не ниже 0,001".

При решении главных геодезических задач с использованием

рядов, чтобы определить требуемое число членов ряда, вводят по-

нятие малой величины первого порядка. За эту величину прини-

мают отношение S к одному из радиусов кривизны эллипсоида

Af, N, R, например S/R). Малой величиной n-го порядка будет

(S/R)

. Тогда необходимое число членов ряда равно такому по-

рядку малости я, которое соответствует требуемой точности вычис-

лений координат и азимутов. Например, при S^30 км, что являет-

ся обычным в триангуляции 1 класса, величина (S/R) «V200. При-

ведем таблицу значений малых величин различных порядков для

этого случая.

Из таблицы видно, что

при Ss£l30 км для решения

главных геодезических за-

дач нужно учитывать четы-

ре первых члена разложения

(17.6). Нетрудно заметить,

что при 5>30 км возникает

необходимость удерживать

большее число членов раз-

ложения для обеспечения

той же точности решения.

Таким образом, при увеличении S исходные формулы становятся

сложнее и решение главных геодезических задач усложняется.

Разложение в ряд Тейлора является одним из методов реше-

ния дифференциальных уравнений (17.4), основанным на аппрок-

Порядок

малости

величины

(S/Rf,

S < 30 км

Выражение малой

величины в гра-

дусной мере

Р "{S/R)

1/2-10

1000"

1/4' Ю

1/8-10

0,02"

1/16-10

0,0001"

277;

симации искомого решения у =

(л:) степенным рядом в функции

от исходных данных к.

В настоящее время, в связи с широким использованием ЭВМ,

появилась возможность применять другие, более эффективные,

численные методы решения дифференциальных уравнений (17.4),

основанные на непосредственном вычислении приращения функции

А у в зависимости от приращения AJC независимой переменной.

К таким методам относится метод Эйлера и Рунге — Кутта.

В геодезической практике наибольшее распространение полу-

чил метод Рунге — Кутта и его модификации. Отличительной осо-

бенностью этих методов является простота программирования,

высокая точность решения, возможность автоматического выбора

шага интегрирования и оценки точности решения, универсальность

и единообразие вычислений при любых расстояниях. При этом ре-

шение прямой геодезической задачи сводится к задаче Коши, в

которой необходимо найти решение обыкновенного дифференци-

ального уравнения

*/' = <р(*, у),

в виде у= <р(*),

(17.7)

(17.8)

удовлетворяющего начальным условиям у(Хо)=уо, которым соот-

ветствуют исходные данные Вi, L

в начальной точке.

Идея метода Рунге — Кутта кратко состоит в следующем.

Решение уравнения (17.7) в точке xj+\ запишется в виде

yj+i =

Уз

yiki =

Н)

(17.9)

где

i-i

^hf(x

jt yj

);

bi = hf ^ + a

h; yj + ^ j ;

h = — Xj = ^x; i — 2, 3,..., n.

(17.10)

Коэффициенты у/, ш, P</ в (17.9) и (17.10) подбираются из ус-

ловия, чтобы несколько первых членов разложения (17.9) в ряд

Тейлора по степеням h совпали с соответствующими членами раз-

ложения по степеням h точного решения yj(Xi + h).

Пусть i=2, / = 0, тогда

Ф/(*0, У0»

) = +

(17.11)

где

= hf (х

, у о);

kt = hf (x

+ aji, t/

+ М:

(14.12)

278