Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.


10 1 Fundamentals in Continuum Mechanics
t
t
dt
t
tdtt
L
xu
L
LL
w
w
|
¿
¾
½
¯
®
,
(1.1.12)
Let us denote
ttt LLȋ and
xL t , since we are taking
tL as an infinitesimal line element, so that we have
¸
¹
·
¨
©
§
w
w
E
x
X
x
X
L
LL
t
ttt
(1.1.13)
and
¸
¹
·
¨
©
§
w
w
w
w
o
u
x
u
x
u
L
xu
0
lim
x
t
t
,
(1.1.14)
where
E is called the displacement gradient tensor and
u
is called the
velocity gradient tensor. Using the notation defined in Eqs. (1.1.13) and
(1.1.14). Thus, the change rate of material line element
tL , which is
given by Eq. (1.1.11), will be written by the formula
Ȧe
¿
¾
½
¯
®
x
uuuuxux
TT
ේේ
2
1
ේේ
2
1
(1.1.15)
where superscript
T
denotes the transpose of tensor. It is noted here that in
expanding Eq. (1.1.15) the velocity gradient tensor u , arbitrary second
order tensor is decomposed into symmetric and skew-symmetric (or anti-
symmetric) parts. We now define the rate of strain (or the rate of deforma-
tion) tensor, as the symmetric part of the velocity gradient tensor
T
uu ේේ
2
1
e
(1.1.16)
and the vorticity (or spin) tensor, as the skew-symmetric part of the veloc-
ity gradient tensor
T
uu ේේ
2
1
Ȧ
(1.1.17)
Thus, the change rate of
tL due to translation
t,xu can be straining
ex and rotation Ȧx . Consequently the velocity gradient tensor can
be written by
'' '
''
'
'
'
'
'
ේ
'
'
''

1.1 Dynamics of Fluid Motion 11
Ȧe u
(1.1.18)
In order to gain more physical insight for tensors
e and Ȧ in contin-
uum mechanics, we will examine
e in the first place. Referring Eq.
(1.1.16),
e can be written by the Cartesian suffix convention for three val-
ues,
i = 1, 2 and 3, or j = 1, 2 and 3, which correspond to
x
,
y
and z
respectively as follows
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
i
j
j
i
jiijji
x
u
x
u
e
2
1
eeee
ˆˆˆˆ
e
(1.1.19)
where
ji
ˆˆ
ee
is the unit dyad (see Appendix B-1), and the components of
the rate of strain tensor
ij
e
is presented by
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
¬
ª
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
333231
232221
131211
3
3
3
2
2
3
3
1
1
3
3
2
2
3
2
2
2
1
1
2
1
3
3
1
1
2
2
1
1
1
2
1
2
1
2
1
2
1
2
1
2
1
eee
eee
eee
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
e
ij
(1.1.20)
It is easily known from Eq. (1.1.20) that
ij
e is the symmetric and has 6 in-
dependent components, i.e.
11
e ,
22
e ,
33
e ,
2112
ee ,
3223
ee and
1331
ee . The
orthogonal components
11
e ,
22
e , and
33
e are the rate of elongational strain,
due to a local deformation of fluid in stretching or contraction in
x
, y ,
and
z
axis respectively. In addition the off-orthogonal components
12
e
,
23
e , and
31
e (as well as
21
e ,
32
e , and
13
e ) are, on the other hand, due to a
local deformation of fluid in shearing in the plane of
x
– y , y –
z
, and
z
–
x
respectively. Figure 1.4 gives an idea of the deformation rate occurring in
fluid in
x
y plane. Figure 1.4 (1)-a shows the simple elongational (or ex-
tensional) flow field as one of typical stretching and contraction of flow,
where the rate of elongational strain appears. Furthermore, in order to
make the point clear, in Fig. 1.4 (1)-b the stretching of a fluid element in
the elongational flow field is indicated. Similarly in Fig. 1.4 (2)-a the dia-
gram shows the simple shear flow field, where the shear strain takes place
and (2)-b a sketch of the shear field is displayed, where a fluid element is
sheared in the flow direction.
–

12 1 Fundamentals in Continuum Mechanics
The symmetry of the tensor e guarantees that there will always be
three mutual orthogonal orientations of
xww Xp
ˆ
, for each of which the
corresponding rate of deformation is either elongation or contraction, that
is the principal rates of deformation, to which we can assign
111
ee
c
,
222
ee
c
and
333
ee
c
. The summations of
1
e
c
,
2
e
c
and
3
e
c
are invariant for
coordinate transformation, which give the proportional rate of increase of
an infinitesimal material volume
321
ේ eeediv
c
c
c
uu
(1.1.21)
(1)-a Simple elongational (2)-a Simple shear flow field
(or extensional ) flow field
Fig. 1.4 Local deformation of fluid
This quantity defined in Eq. (1.1.21) is called the divergence of the veloc-
ity field of
t,xu
. Furthermore, a definition that is independent from a
coordinates system can be given by
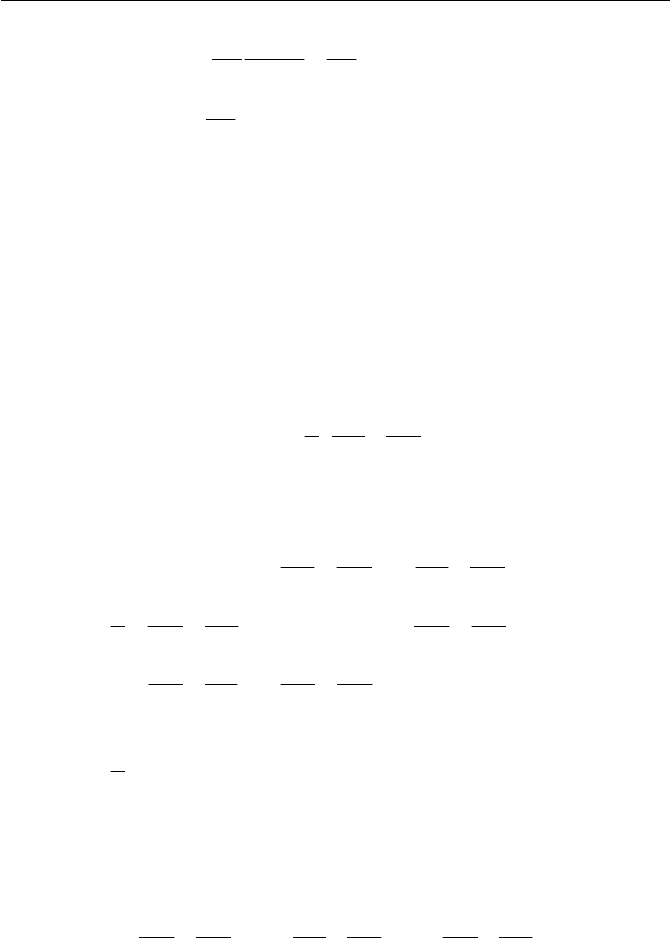
1.1 Dynamics of Fluid Motion 13
³
³
V
S
dV
V
dS
VDt
VD
V
div
u
unu
G
G
G
G
1
11
ˆ
(1.1.22)
Equation (1.1.22) is called the Euler’s relation, which implies the physical
rate of change over time of the volume of moving fluid particles per unit
volume. It is noted that to write the volume integral
³
V
dVu from the
surface integral
³
S
dSun
ˆ
the Gauss’ divergence theorem is applied.
The skew-symmetric part
Ȧ given by Eq. (1.1.17) of the velocity gra-
dient tensor
u can be similarly written by the Cartesian suffix conven-
tion as
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
i
j
j
i
jiijji
x
u
x
u
2
1
eeee
ˆˆˆˆ
Ȧ
Z
(1.1.23)
and
ij
Z
can be further written in matrix form
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
¬
ª
¸
¹
·
¨
©
§
w
w
w
w
¸
¹
·
¨
©
§
w
w
w
w
¸
¹
·
¨
©
§
w
w
w
w
¸
¹
·
¨
©
§
w
w
w
w
¸
¹
·
¨
©
§
w
w
w
w
¸
¹
·
¨
©
§
w
w
w
w
0
0
0
2
1
0
0
0
2
1
3231
2321
1312
3
2
2
3
3
1
1
3
2
3
3
2
2
1
1
2
1
3
3
1
1
2
2
1
ZZ
ZZ
ZZ
Z
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
ij
(1.1.24)
Components, which appear in Eq. (1.1.23), as the components of
uȦ u
, are related with the following formula
332211
2
1
1
2
3
1
3
3
1
2
3
2
2
3
1
ZZZ
eee
eeeu
ˆˆˆ
ˆˆˆ
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
u
x
u
x
u
x
u
x
u
x
u
x
u
(1.1.25)

14 1 Fundamentals in Continuum Mechanics
It may be useful to consider uȦ u in a little more detail for the
sake of coupling equations in the following chapters. The nature of
uu
can be examined by introducing the alternator or alternating unit tensor
ijkkji
H
eee
ˆˆˆ
İ
as follows
332211
2
1
1
2
3
1
3
3
1
2
3
2
2
3
1
332211
ZZZ
HHH
H
eee
eee
eee
eu
ˆˆˆ
ˆˆˆ
ˆˆˆ
ˆ
¸
¹
·
¨
©
§
w
w
w
w
¸
¹
·
¨
©
§
w
w
w
w
¸
¹
·
¨
©
§
w
w
w
w
w
w
w
w
w
w
w
w
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
j
k
jk
j
k
jk
j
k
jk
j
k
iijk
(1.1.26)
Thus, in comparison with (1.1.23) and (1.1.25), a vector
Ȧ (in this case
uu
) with components
1
Z
,
2
Z
and
3
Z
can be reduced from a general
second order tensor
S
(in the present case
ji
xu ww , xu ww , u or
ugrad ), whose components of skew-symmetric part (in this case Ȧ ) are
written by
»
»
»
¼
º
«
«
«
¬
ª
0
0
0
2
1
12
1
3
23
ZZ
ZZ
ZZ
Ȧ
(1.1.27)
Note that the vector
321
Z
Z
Z
,, Ȧ is called the pseudovector of the tensor
S or simply the vector of tensor S . See Exercise 1.4.
By employing the alternator
İ , the vector Ȧ may be found from S ,
more specifically from the skew-symmetric part
a
S of
S
, denoting
2
a
ȦS while the symmetric part
s
S of S may be expressed by
2
s
eS
. The following relationships are particularly useful;
Sİ Ȧ
(1.1.28)
Ȧ İS
2
1
a
(1.1.29)
Note that from Eqs. (1.1.28) and (1.1.29) the pseudovector
Ȧ is zero,
0
Ȧ , if a second order tensor S is symmetric 0
a
S , and vice versa.

1.1 Dynamics of Fluid Motion 15
For the sake of clarity and convenience, the unit tensor I and the al-
ternator
İ
are defined below. I is defined such that
ijji
G
ee
ˆˆ
I
(1.1.30)
where
ij
G
is the Kronecker delta and
ji
ee
ˆˆ
is the unit dyad.
ij
G
is defined
as
¿
¾
½
¯
®
z
ji
ji
ij
if0
if1
G
(1.1.31)
İ is similarly defined by
ijkkji
H
eee
ˆˆˆ
İ
(1.1.32)
where
ijk
H
is the Eddington notation and
kji
eee
ˆˆˆ
is the unit polyadic. Thus,
the alternator is a polyadic.
ijk
H
is defined in the following manner
°
¯
°
®
kjkiji
ijk
ijk
ijk
or,,if0
213or,132,321if1
312or,231,123if1
H
(1.1.33)
It is useful for
İ to be alternatively expressed with the form
123312231213132321
ˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆˆ
İ
eeeeeeeeeeeeeeeeee
(1.1.34)
After giving mathematical formalities for the tensor
Ȧ , we will see
how
Ȧ may cause a local deformation in the flow field
t,xu . The de-
formation due to
Ȧ
can be examined from Eq. (1.1.11) as
dttdtt
a
»
¼
º
«
¬
ª
¸
¹
·
¨
©
§
w
w
|
L
u
LLLX )()(
(1.1.35)
Note that
a
Lu ww is a skew-symmetric part of the velocity gradient ten-
sor. It is further noted that by taking an infinitesimal time duration tdt
G
|
and on infinitesimal line element
xxL
G
|
, we can obtain the deforma-
tion in
x
- y plane, for example
>@
333
33
3
2
1
2
1
000
00
00
0
2
1
e
exX
ˆ
ˆ
,,Ȧ
txy
tyxt
GZGZG
GZ
Z
GGGG
¸
¹
·
¨
©
§
»
»
»
¼
º
«
«
«
¬
ª
ᇫᇫᇫᇫᇫᇫᇫ
(1.1.36)
'
'
'
16 1 Fundamentals in Continuum Mechanics
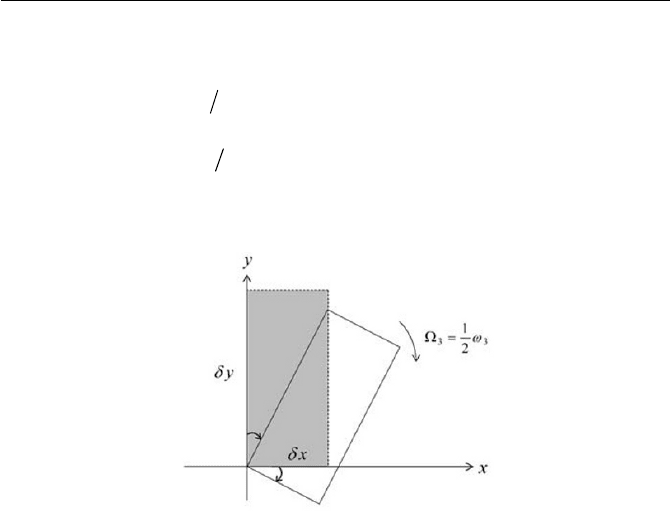
The implication of Eq. (1.1.36) is, in the
x
– y plane, that as indicated in
Fig. 1.5, the fluid element x
G
– y
G
is rotated around the z axis with its an-
gular velocity
2
33
Z
. Thus, as easily speculated from Fig. 1.5, the
vorticity tensor
Ȧ represents a rigid body rotation of fluid element with
angular velocity
2Ȧ
. The pseudovector of the velocity gradient ten-
sor, i.e.
uuȦ u :İේ , is called the vorticity vector. The vorticity
vector
Ȧ is an important flow parameter in fluid mechanics.
Fig. 1.5 Rigid body rotation of fluid element
x
G
y
G
1.2 Dynamics in Rotating Reference Frame
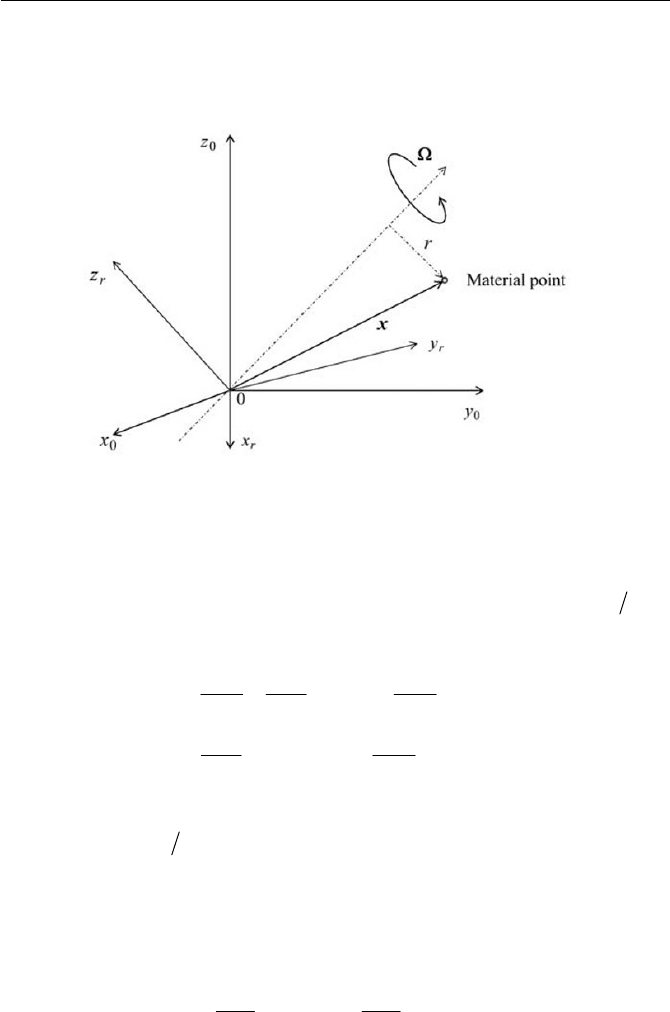
In consideration of kinematics let us explore the relationship between an
inertial and a rotating reference frame. For brevity, let the rotating refer-
ence frame be rotated with a constant angular velocity with respect to
the inertial reference frame, supposing no translation of the rotating refer-
ence frame to the inertial reference frame, see Fig. 1.6. It is noted that we
adopt a right-handed orthogonal coordinates system, where
0!
is an
angular velocity vector, which rotates to the direction of a right-handed
screw. The position vectors
0
x and
r
x of a material point x in the iner-
tial frame and rotating frame respectively are related as
0
xx Q
r
(1.2.1)
where
Q is a rotation tensor, which is an orthogonal tensor with a relation
of
IQQ
T
, and
1
QQ
T
(where Q is an unitary matrix);
1
Q
:
–
:
:
:
1.2 Dynamics in Rotating Reference Frame 17
denotes the inverse of the tensor Q and
T
Q denotes the transpose of the
tensor
Q .
Fig. 1.6 Rotating reference frame with inertial reference frame
In order to correlate two frames kinematically, we shall consider a ve-
locity and acceleration at the material point. To start with, apply
DtD ,
the material derivative, to Eq. (1.2.1) to obtain the relative velocity
r
u
Dt
D
Dt
D
Dt
D
Dt
D
Dt
D
r
r
r
0
1
0
0
x
x
x
x
x
u
QQ
Q
Q
Q
(1.2.2)
Equation (1.2.2) can be further written with the velocity
0
u in the inertial
frame, letting
00
ux DtD by
0
uxu u Q
rr
(1.2.3)
Here we used tensor calculus (for relative position vector
r
x , see Problem
1-1) as
rr
T
r
Dt
D
Dt
D
xxx u
1
Q
Q
Q
Q
(1.2.4)
:
:

18 1 Fundamentals in Continuum Mechanics
It is noted that is the pseudovector of the skew-symmetric tensor
T
DtD QQ
in the same manner explained for the vorticity vector Ȧ
previously. Next, by taking the material derivative again to Eq. (1.2.3), we
can obtain the relative acceleration
r
a of the material point x as follows
0
11
axuu
u
a
uu
QQ
Q
Q
Q
rrr
r
r
Dt
D
Dt
D
Dt
D
(1.2.5)
Consequently from Eq. (1.1.4), we can obtain the acceleration vector
0
a ,
i.e. the acceleration of the inertial frame, by relating Eq. (1.2.5) in the ro-
tating frame as
rrr
xuaa uuu 2
0
(1.2.6)
where it is derived when an inertial frame is instantaneously coincident
with the rotating frame , as
IQ
. In Eq. (1.2.6), the first term in the right
hand side of the equation is the rectilinear acceleration, the second is the
Corioli’s acceleration, and the third is the centripetal acceleration. With
identical vectors, it is easy to show that the third term of Eq. (1.2.6), i.e.
the centripetal acceleration can be reduced to the potential form as
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
u uu
22
2
2
1
2
1
r
rr
xx
(1.2.7)
so that, defining a potential function
I
, and setting 2
22
r
I
, where
r
simply denotes distance from the axis of rotation, the centripetal accelera-
tion can be expressed as
I
uu
r
x
(1.2.8)
It may be worthwhile to note that the operation to reduce the relation
(1.2.6) can be simply understood by a vector algebra for a fluid particle ro-
tating at a constant angular velocity along an axis of rotation in the in-
ertial reference frame at a material point
x
r
xx
0
(1.2.9)
and
rr
xuu u
0
(1.2.10)
Equation (1.2.9) refers to the instantaneous moment, when IQ , and Eq.
(1.2.10) implies the relative velocity of the fluid particle rotating to the
:
:
:
::
:: :
: : :
: :
:
:

1.3 Material Objectivity and Convective Derivatives 19
inertial frame. Thus, taking the time derivative to Eq. (1.2.10), as we have
similarly done to Eq. (1.2.3), we can obtain the acceleration of the fluid
particle relative to the inertial frame as
rr
r
dt
d
Dt
D
xu
uu
a uuu 2
0
0
(1.2.11)
which is exactly the same form as Eq. (1.2.6). The relation given by Eq.
(1.2.11) can again be written, using the potential
I
I
ේ2
0
u
rr
uaa
(1.2.12)
where
2
22
r
I
.
1.3 Material Objectivity and Convective Derivatives
On the microstructure level material elements may be affected by strong
electromagnetic field or strong inertial forces; however, on the continuum
level the physical characteristic of a material, such as demonstrated by the
Hooke’s law (the relationship between the extension and the force can be
regarded as a physical property of spring itself), is independent of the mo-
tion of the observer. This concept is called “the material objectivity” or
“the principle of frame invariance”. Particularly in dealing with the rela-
tionship between a deformation and a stress in continuum, so-called consti-
tutive equation, this concept is of some importance.
In order to satisfy the principle of frame invariance, the following lin-
ear transformation by
E (see
Q
and E in Eqs. (1.2.1) and (1.3.4) for
equivalence) must be satisfied for any arbitrary vectors (say a velocity vec-
tor ),( t
xu ) and second order tensor (say a stress tensor )( t,T x ) in the
Cartesian reference frame. This can be set in the inertial reference frame
in such a way that
0
uu Q
r
to E uu
(1.3.1)
T
r
QTQT
0
to
T
ETET
(1.3.2)
where the suffix
r
denotes the rotating reference frame. Note that scalar
properties (such temperature, density, etc.) are always frame invariant.
Now we will direct our attention to how the time derivative of vectors
and tensors are affected in order for the principle of frame invariance to be
satisfied. We will consider this problem with respect to the transformation
:
'
'
: : :
:
