Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.


Appendix B
lijklkjilkji
eeeeeeeeee
ˆˆˆˆˆˆˆˆˆˆ
G
(B.1-4)
lijklkjikji
eeeeeeee
ˆˆ
İ
ˆˆˆˆˆˆ
u u
(B.1-5)
klijlkjikji
eeeeeeee
ˆˆ
İ
ˆˆˆˆˆˆ
u u
(B.1-6)
Appendix B-2 Representative Operations
uuu II
(B.2-1)
wvuwuv
(B.2-2)
vuwuvw
(B.2-3)
zuvwvzuwwzuv
::
(B.2-4)
vuuv T:T
(B.2-5)
>@
TT: vuuv
(B.2-6)
Appendix B-3 Differential Operators
Cartesian Coordinates
zyx
zyx
w
w
w
w
w
w
eee
ˆˆˆ
(B.3-1)
Cylindrical Coordinates
zrr
zr
w
w
w
w
w
w
eee
ˆˆˆ
T
T
1
(B.3-2)
Spherical Coordinates
ITT
IT
w
w
w
w
w
w
sin
11
rrr
r
eee
ˆˆˆ
(B.3-3)
Appendix B-4 Operations
(i) Representative
operations
in Cartesian Coordinates
zyx ,,
545

Appendix
z
u
y
u
x
u
z
y
x
w
w
w
w
w
w
u
(B.4-1)
2
2
2
2
2
2
2
z
s
y
s
x
s
s
w
w
w
w
w
w
(B.4-2)
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
z
u
T
y
u
T
x
u
T
z
u
T
y
u
T
x
u
T
z
u
T
y
u
T
x
u
T
z
zz
z
zy
z
zx
y
yz
y
yy
y
yx
x
xz
x
xy
x
xx
u:T
(B.4-3)
(ii) Representative
operations
in Cylindrical Coordinates
zr ,,
T
z
u
u
r
ru
rr
z
r
w
w
w
w
w
w
T
T
11
u
(B.4-4)
2
2
2
2
2
2
11
z
ss
r
r
s
r
rr
s
w
w
w
w
w
w
w
w
T
(B.4-5)
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
z
u
T
u
r
T
r
u
T
z
u
T
r
uu
r
T
r
u
T
z
u
T
r
uu
r
T
r
u
T
z
zz
z
z
z
zr
z
r
r
r
rz
r
r
r
rr
T
T
T
T
T
T
T
TT
T
T
T
T
1
1
1
: uT
(B.4-6)
(iii) Representative
operations
in Spherical Coordinates
I
T
,r,
IT
T
TT
I
T
w
w
w
w
w
w
u
r
u
r
ur
r
r
r
sin
1
sin
sin
11
2
2
u (B.4-7)
546

Appendix B
2
2
222
2
2
2
sin
1
sin
sin
11
IT
T
T
T
T
w
w
¸
¹
·
¨
©
§
w
w
w
w
¸
¹
·
¨
©
§
w
w
w
w
s
r
s
r
r
s
r
r
r
s (B.4-8)
9)-(B.4 cot
sin
1
1
cot
sin
11
sin
11
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
T
IT
T
T
ITT
ITT
T
I
II
I
IT
I
I
I
T
TI
T
TT
T
T
I
I
T
T
r
u
r
u
u
r
T
u
r
T
r
u
T
r
u
u
r
T
r
uu
r
T
r
u
T
r
u
u
r
T
r
uu
r
T
r
u
T
r
r
r
r
r
r
r
r
r
rr
u:T
Appendix B-5 Representative Differential Relations
0 u s
(B.5-1)
0 u u
(B.5-2)
rssrrs
(B.5-3)
uuu sss
(B.5-4)
uuu uu u sss
(B.5-5)
uwwu
uwwuwu
uuuu
(B.5-6)
wuuwwu u
u u
(B.5-7)
wuuw
uwwuwu
uu
(B.5-8)
uuu
2
uu
(B.5-9)
uuu uu
(B.5-10)
547

Appendix
0 u rs
(B.5-11)
uuuuuu uu
2
1
(B.5-12)
uwwuuw
(B.5-13)
uue ss :
ˆ
(B.5-14)
ss e
ˆ
(B.5-15)
TTT sss
(B.5-16)
T
a
a
TTT
T,T
u
2
1
where
vec
2
1
AA
(B.5-17)
Appendix B-6 Equation of Continuity
0
w
w
u
U
U
t
Cartesian Coordinates
zyx ,,
0
w
w
w
w
w
w
w
w
zyx
u
z
u
y
u
xt
UUU
U
(B.6-1)
Cylindrical Coordinates
zr ,,
T
0
11
w
w
w
w
w
w
w
w
zr
u
z
u
r
ru
rrt
UU
T
U
U
T
(B.6-2)
Spherical Coordinates
I
T
,,r
0
sin
1
sin
sin
11
2
2
w
w
w
w
w
w
w
w
IT
U
IT
TU
TT
U
U
u
r
u
r
ur
r
r
t
r
(B.6-3)
When the fluid is assumed to have constant mass density
U
, the equa-
tion simplifies to 0
u
548

Appendix B
Appendix B-7 Equation of Motion in Terms of Stress Tensor IJ
gIJ
UU
p
D
t
Du
(i) Cartesian Coordinates
zyx ,,
xzxyxxx
x
z
x
y
x
x
x
g
zyxx
p
z
u
u
y
u
u
x
u
u
t
u
UWWW
U
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
(B.7-1)
yzyyyxy
y
z
y
y
y
x
y
g
zyxy
p
z
u
u
y
u
u
x
u
u
t
u
UWWW
U
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
(B.7-2)
zzzyzxz
z
z
z
y
z
x
z
g
zyxz
p
z
u
u
y
u
u
x
u
u
t
u
UWWW
U
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
(B.7-3)
(ii) Cylindrical Coordinates
zr ,,
T
rzrrrr
r
z
rr
r
r
g
rzr
r
rrr
p
r
u
z
u
u
u
r
u
r
u
u
t
u
U
W
WW
T
W
T
U
TT
T
TT
¿
¾
½
¯
®
w
w
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
11
2
(B.7-4)
TTTTT
TTTTTT
UWW
T
W
T
T
U
g
zr
r
rr
p
r
r
uu
z
u
u
u
r
u
r
u
u
t
u
zr
r
zr
¿
¾
½
¯
®
w
w
w
w
w
w
w
w
¸
¹
·
¨
©
§
w
w
w
w
w
w
w
w
111
2
2
(B.7-5)
549

Appendix
zzzzrz
z
z
zz
r
z
g
zr
r
rrz
p
z
u
u
u
r
u
r
u
u
t
u
UWW
T
W
T
U
T
T
¿
¾
½
¯
®
w
w
w
w
w
w
w
w
¸
¹
·
¨
©
§
w
w
w
w
w
w
w
w
11
(B.7-6)
(iii) Spherical Coordinates
I
T
,,r
7)(B.7-
sin
1
sin
sin
11
sin
2
2
22
r
rrrr
rrr
r
r
g
rrr
r
rrr
p
r
uuu
r
uu
r
u
r
u
u
t
u
U
WW
W
IT
TW
TT
W
ITT
U
IITT
IT
ITI
T
¿
¾
½
¯
®
w
w
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
8)-(B.7
cot
sin
1
sin
sin
11
1
cot
sin
2
2
2
T
IIT
ITTTT
ITTITTTT
U
TWW
W
IT
TW
TT
W
T
T
ITT
U
g
rrr
r
rr
p
r
r
uuuu
r
uu
r
u
r
u
u
t
u
r
r
r
r
¿
¾
½
¯
®
w
w
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
9)-(B.7
cot2
sin
111
sin
1
cot
sin
2
2
I
TIII
IITII
ITIIIITII
U
TWWW
W
IT
W
T
W
IT
T
ITT
U
g
rrr
r
rr
p
r
r
uuuuu
r
uu
r
u
r
u
u
t
u
rr
r
r
r
¿
¾
½
¯
®
w
w
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
550

Appendix B
Appendix B-8 Equation of Motion for a Newtonian Fluid with Constant
U
and
0
K
gu
u
UKU
2
0
Dt
D
p
(i) Cartesian Coordinates
zyx ,,
x
xxx
x
z
x
y
x
x
x
g
z
u
y
u
x
u
x
p
z
u
u
y
u
u
x
u
u
t
u
UK
U
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
2
2
2
2
2
2
0
(B.8-1)
y
yyy
y
z
y
y
y
x
y
g
z
u
y
u
x
u
y
p
z
u
u
y
u
u
x
u
u
t
u
UK
U
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
2
2
2
2
2
2
0
(B.8-2)
z
zzz
z
z
z
y
z
x
z
g
z
u
y
u
x
u
z
p
z
u
u
y
u
u
x
u
u
t
u
UK
U
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
2
2
2
2
2
2
0
(B.8-3)
(ii) Cylindrical Coordinates
zr ,,
T
r
rr
r
r
z
rr
r
r
g
u
rz
uu
r
ru
rrrr
p
r
u
z
u
u
u
r
u
r
u
u
t
u
U
TT
K
T
U
T
TT
¿
¾
½
¯
®
w
w
w
w
w
w
¸
¹
·
¨
©
§
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
22
2
2
2
2
0
211
2
(B.8-4)
T
TT
T
TTTTTT
U
T
T
K
T
T
U
g
u
rz
uu
r
ru
rrr
p
r
r
uu
z
u
u
u
r
u
r
u
u
t
u
r
r
zr
¿
¾
½
¯
®
w
w
w
w
w
w
w
w
w
w
w
w
¸
¹
·
¨
©
§
w
w
w
w
w
w
w
w
22
2
2
2
2
0
2111
(B.8-5)
551
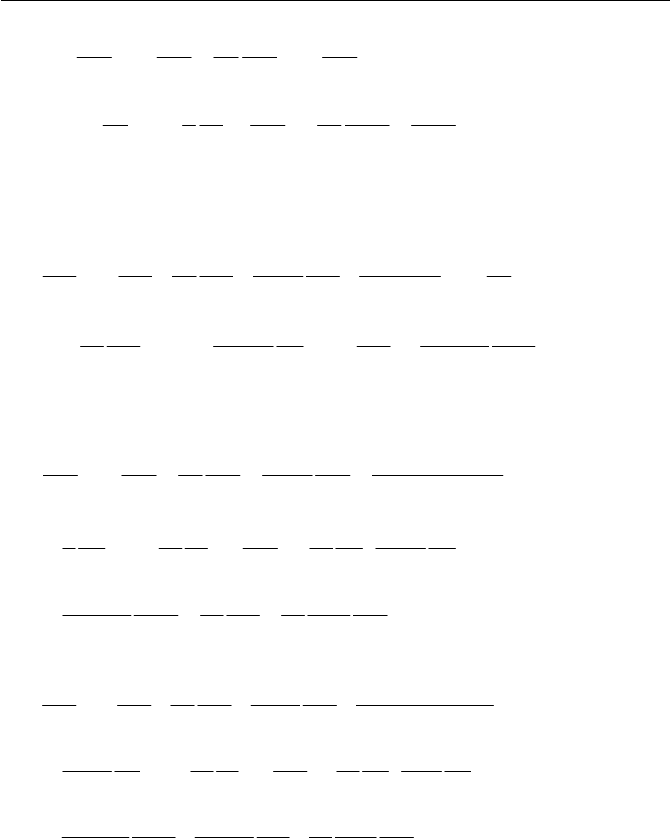
Appendix
z
zzz
z
z
zz
r
z
g
z
uu
rr
u
r
rrz
p
z
u
u
u
r
u
r
u
u
t
u
U
T
K
T
U
T
¿
¾
½
¯
®
w
w
w
w
¸
¹
·
¨
©
§
w
w
w
w
w
w
¸
¹
·
¨
©
§
w
w
w
w
w
w
w
w
2
2
2
2
2
0
11
(B.8-6)
(iii) Spherical Coordinates
I
T
,,r
r
rr
r
rrr
r
r
g
u
r
u
r
ur
rr
r
p
r
uuu
r
uu
r
u
r
u
u
t
u
U
ITT
T
TT
K
ITT
U
ITIT
¿
¾
½
¯
®
w
w
¸
¹
·
¨
©
§
w
w
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
2
2
222
2
2
2
2
0
22
sin
1
sin
sin
11
sin
(B.8-7)
T
I
T
T
T
IT
T
I
TTTT
U
IT
T
TIT
T
TTT
K
T
T
ITT
U
g
u
r
u
r
u
r
u
rrr
u
r
rr
p
r
r
uuu
u
r
u
u
r
u
r
u
u
t
u
r
r
r
¿
¾
½
w
w
w
w
w
w
¯
®
¸
¹
·
¨
©
§
w
w
w
w
¸
¹
·
¨
©
§
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
sin
cot22
sin
1
sin
sin
1111
cot
sin
222
2
22
2
2
2
0
2
(B.8-8)
I
TI
I
I
ITIIIITII
U
IT
T
ITIT
T
TTT
K
IT
T
ITT
U
g
u
r
u
r
u
r
u
rr
u
r
rr
p
r
r
uuuuu
r
uu
r
u
r
u
u
t
u
r
r
r
¿
¾
½
w
w
w
w
w
w
¯
®
¸
¹
·
¨
©
§
w
w
w
w
¸
¹
·
¨
©
§
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
sin
cot2
sin
2
sin
1
sin
sin
111
sin
1
cot
sin
222
2
22
2
2
2
0
(B.8-9)
552
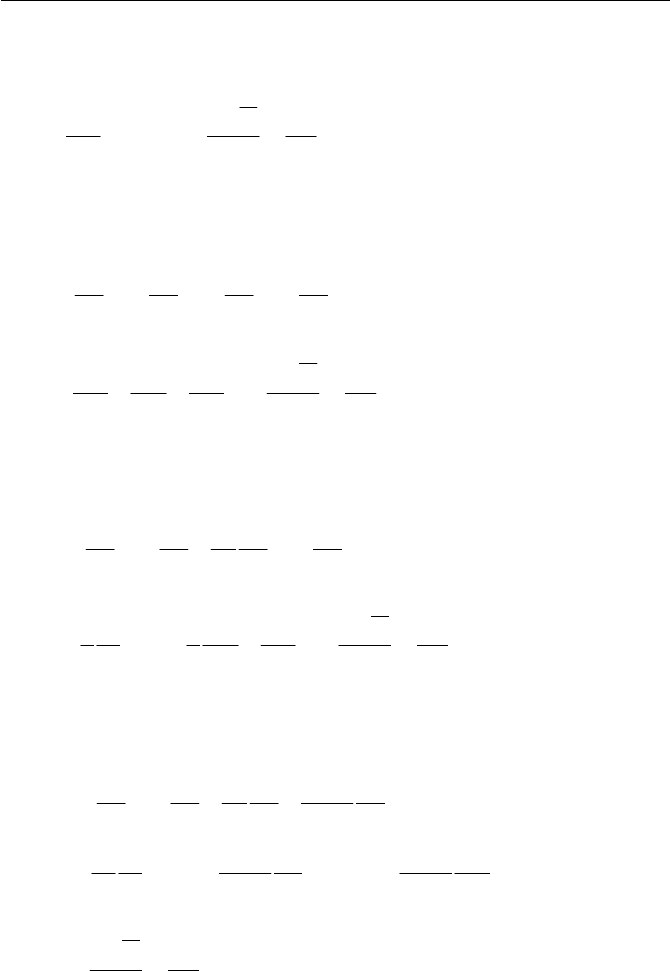
Appendix B
Appendix B-9 Equation of Energy in Terms of q (b=0)
uq
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
©
§
w
w
:IJ
Dt
D
ln
1
ln
Dt
D p
T
T
c
p
p
U
U
(i) Cartesian Coordinates
zyx ,,
u
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
:IJ
Dt
D
ln
1
ln
p
Tz
q
y
q
x
q
z
T
u
y
T
u
x
T
u
t
T
c
p
z
y
x
zyxp
U
U
(B.9-1)
(ii) Cylindrical Coordinates
zr ,,
T
u
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
w
w
w
w
¸
¹
·
¨
©
§
w
w
w
w
w
w
w
w
:IJ
Dt
D
ln
1
ln
11 p
Tz
qq
r
rq
rr
z
T
u
T
r
u
r
T
u
t
T
c
p
z
r
zrp
U
T
T
U
T
T
(B.9-2)
(iii) Spherical Coordinates
I
T
,,r
u
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
:IJ
Dt
D
ln
1
ln
sin
1
sin
sin
11
sin
2
2
p
T
q
r
q
r
qr
rr
T
r
u
T
r
u
r
T
u
t
T
c
p
r
rp
U
IT
T
TT
ITT
U
I
T
I
T
(B.9-3)
553

Appendix
Appendix C
Appendix C-1 Buckingham -Theorem
The Buckingham
S
-theorem is used in the study of dimensional analysis
and similitude, which is based on the notion of dimensional homogeneity.
The theorem is examined in a given fluid system where variables of
1
q
,
2
q
,
…,
n
q
are chosen so that they are pertinent to a physical phenomena.
Then, we will express the phenomena by a functional form as
0
321
n
qqqqf ,...,,,
(C.1-1)
where n represents the total number of variables. If there are m basic di-
mensions involved in the variables of
1
q
~
n
q
, the Buckingham
S
-
theorem states that the same physical phenomena can be correlated by
mn
nondimensional numbers (independent from nondimensional
groups), called
S
-parameters, which are given as a functional form
0
321
mnಣ
SSSS
,...,,,g
(C.1-2)
When a given fluid system contains a dependent variable, say
1
q
, the
physical phenomenon can be expressed similarly in the form
n
qqqhq ,...,,
321
(C.1-3)
and
mn
s
ಣ
SSSS
,...,,
321
(C.1-4)
where
1
S
includes the dependent variable and the remaining
S
-
parameters include the rest of independent variables. The procedure
adopted for determining the nondimensional
S
-parameters are as follows;
Step (1) In having written the functional form of either Eq. (C.1-1) or Eq.
(C.1-3), select
m repeating the variables from
n
-independent
variables in Eq. (C.1-1) or
1n
-independent variables in Eq.
(C.1-3). The repeating variables must include all of the basic di-
mensions, but they must not form
S
-parameters by themselves.
In order to obtain the most significant
S
-parameters, it is desir-
able to choose one variable with geometric characteristics, sec-
ond variable with flow characteristics and another variable with
fluid properties, such as
l
,
U
and
U
respectively, with reference
to Table C.1. For example, writing Eq. (C.1-1)
ʌ
554
