Занг В.Б. Синергетическая экономика. Время и перемены в нелинейной экономической теории

Подождите немного. Документ загружается.

ɱɬɨ ɡɧɚɱɟɧɢɹ ɩɚɪɚɦɟɬɪɨɜ, ɩɪɢ ɤɨɬɨɪɵɯ ɢɦɟɸɬ ɦɟɫɬɨ ɬɚɤɢɟ ɤɚɱɟɫɬɜɟɧɧɵɟ ɢɡɦɟɧɟɧɢɹ,

ɧɚɡɵɜɚɸɬɫɹ ɛɢɮɭɪɤɚɰɢɨɧɧɵɦɢ. Ⱦɥɹ ɩɨɥɧɨɝɨ ɩɨɧɢɦɚɧɢɹ ɩɨɜɟɞɟɧɢɹ ɫɢɫɬɟɦɵ ɡɧɚɧɢɟ

ɟɟ ɛɢɮɭɪɤɚɰɢɨɧɧɵɯ ɩɚɪɚɦɟɬɪɨɜ ɚɛɫɨɥɸɬɧɨ ɧɟɨɛɯɨɞɢɦɨ. Ɋɚɫɫɦɨɬɪɢɦ ɫɥɟɞɭɸɳɟɟ

ɷɜɨɥɸɰɢɨɧɧɨɟ ɭɪɚɜɧɟɧɢɟ:

ɝɞɟ ɯ ɨɩɪɟɞɟɥɟɧɨ ɜ ɧɟɤɨɬɨɪɨɦ ɩɪɨɫɬɪɚɧɫɬɜɟ, r ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɜɟɤɬɨɪ

ɩɚɪɚɦɟɬɪɨɜ, ɚ f — ɜɟɤɬɨɪ-ɮɭɧɤɰɢɹ, ɭɞɨɜɥɟɬɜɨɪɹɸɳɚɹ ɨɩɪɟɞɟɥɟɧɧɵɦ ɬɪɟɛɨɜɚɧɢɹɦ.

ɍ ɧɟɝɨ ɦɨɝɭɬ ɛɵɬɶ ɪɟɲɟɧɢɹ ɪɚɡɥɢɱɧɵɯ ɬɢɩɨɜ — (I) ɩɨɫɬɨɹɧɧɵɟ, (II) ɩɟɪɢɨɞɢɱɟɫɤɢɟ,

(III)

ɫɭɛɝɚɪɦɨɧɢɱɟɫɤɢɟ, (IV) ɚɫɢɦɩɬɨɬɢɱɟɫɤɢ ɤɜɚɡɢɩɟɪɢɨɞɢɱɟɫɤɢɟ ɢ ɬ.ɩ.

Ɋɚɫɫɦɨɬɪɢɦ ɫɥɭɱɚɣ ɪɚɜɧɨɜɟɫɢɹ f(x,r) = 0. ȿɫɥɢ ɨɫɨɛɨ ɧɟ ɨɝɨɜɨɪɟɧɨ, ɞɚɥɟɟ ɜɫɟɝɞɚ

ɛɭɞɟɦ ɩɪɟɞɩɨɥɚɝɚɬɶ, ɱɬɨ f ɞɢɮɮɟɪɟɧɰɢɪɭɟɦɚ ɫɬɨɥɶɤɨ ɪɚɡ, ɫɤɨɥɶɤɨ ɷɬɨ ɧɟɨɛɯɨɞɢɦɨ.

ɉɨɥɨɠɟɧɢɟ ɪɚɜɧɨɜɟɫɢɹ ɦɵ ɦɨɠɟɦ ɪɚɫɫɦɚɬɪɢɜɚɬɶ ɤɚɤ ɮɭɧɤɰɢɸ ɩɚɪɚɦɟɬɪɨɜ. ɉɪɢ

ɡɚɞɚɧɧɨɦ ɧɚɛɨɪɟ ɩɚɪɚɦɟɬɪɨɜ ɭɪɚɜɧɟɧɢɟ ɱɚɫɬɨ ɦɨɠɟɬ ɢɦɟɬɶ ɧɟ ɨɞɧɨ, ɚ ɧɟɫɤɨɥɶɤɨ

ɩɨɥɨɠɟɧɢɣ ɪɚɜɧɨɜɟɫɢɹ, ɢ ɨɫɧɨɜɧɨɣ ɜɨɩɪɨɫ, ɤɨɬɨɪɵɣ ɦɵ ɡɞɟɫɶ ɧɚɦɟɪɟɧɵ ɨɛɫɭɞɢɬɶ,

ɫɨɫɬɨɢɬ ɜ ɬɨɦ, ɤɚɤ ɪɚɜɧɨɜɟɫɢɟ ɡɚɜɢɫɢɬ ɨɬ ɩɚɪɚɦɟɬɪɨɜ ɡɚɞɚɱɢ.

ɉɭɫɬɶ ɞɥɹ ɭɞɨɛɫɬɜɚ x ɢ r ɩɪɢɧɚɞɥɟɠɚɬ R

. Ȼɢɮɭɪɤɚɰɢɨɧɧɚɹ (ɫɬɚɬɢɱɟɫɤɚɹ) ɡɚɞɚɱɚ

ɷɤɜɢɜɚɥɟɧɬɧɚ ɢɫɫɥɟɞɨɜɚɧɢɸ ɤɪɢɜɵɯ f(x,r) = 0 ɢ ɢɯ ɨɫɨɛɵɯ ɬɨɱɟɤ. Ɉɫɧɨɜɧɵɦ

ɢɧɫɬɪɭɦɟɧɬɨɦ ɞɨɤɚɡɚɬɟɥɶɫɬɜɚ ɫɭɳɟɫɬɜɨɜɚɧɢɹ ɪɟɲɟɧɢɣ ɜ ɬɟɨɪɢɢ ɛɢɮɭɪɤɚɰɢɣ

ɹɜɥɹɟɬɫɹ ɬɟɨɪɟɦɚ ɨ ɧɟɹɜɧɨɣ ɮɭɧɤɰɢɢ ɞɥɹ ɜɟɤɬɨɪɧɨɡɧɚɱɧɵɯ ɮɭɧɤɰɢɣ ɦɧɨɝɢɯ

ɩɟɪɟɦɟɧɧɵɯ (ɫɦ., ɧɚɩɪɢɦɟɪ, ɑɭ ɢ ɏɟɣɥ, 1982). ȼ ɨɞɧɨɦɟɪɧɨɦ ɫɥɭɱɚɟ ɷɬɭ ɬɟɨɪɟɦɭ

ɦɨɠɧɨ ɫɮɨɪɦɭɥɢɪɨɜɚɬɶ ɫɥɟɞɭɸɳɢɦ ɨɛɪɚɡɨɦ:

Ʌɟɦɦɚ. (Ɍɟɨɪɟɦɚ ɨ ɧɟɹɜɧɨɣ ɮɭɧɤɰɢɢ ɜ R

.) ɉɭɫɬɶ f(x

) = 0 ɢ f ɩɪɢɧɚɞɥɟɠɢɬ

ɤɥɚɫɫɭ ɋ

ɜ ɧɟɤɨɬɨɪɨɣ ɨɬɤɪɵɬɨɣ ɨɤɪɟɫɬɧɨɫɬɢ ɬɨɱɤɢ (x

) ɧɚ ɩɥɨɫɤɨɫɬɢ (x,r). Ɍɨɝɞɚ

ɟɫɥɢ f

≠0, ɬɨ ɫɭɳɟɫɬɜɭɸɬ ɬɚɤɢɟ

>0, ɱɬɨ (I) ɜɫɹɤɢɣ ɪɚɡ, ɤɨɝɞɚ x

< ɯ < ɯ

< r < r

, ɭɪɚɜɧɟɧɢɟ f(x, r) = 0 ɢɦɟɟɬ ɟɞɢɧɫɬɜɟɧɧɨɟ ɪɟɲɟɧɢɟ ɯ = ɯ(r), ɢ (II)

ɫɭɳɟɫɬɜɭɟɬ x

(r), ɩɪɢɱɟɦ x

(r) = -f

(x(r)/f

(x(r),r).

Ɇɨɠɧɨ ɩɪɨɜɟɫɬɢ ɫɥɟɞɭɸɳɭɸ ɤɥɚɫɫɢɮɢɤɚɰɢɸ ɬɨɱɟɤ, ɩɪɢɧɚɞɥɟɠɚɳɢɯ ɤɪɢɜɵɦ

ɪɟɲɟɧɢɣ (ɫɦ. Ƀɨɫɫ ɢ Ⱦɠɨɡɟɮ, 1980, Ȼɪɢɬɬɨɧ, 1986).

Ɉɩɪɟɞɟɥɟɧɢɟ 3.7.1. (Ɉɞɧɨɦɟɪɧɵɣ ɫɥɭɱɚɣ.)

Ɋɟɝɭɥɹɪɧɨɣ ɬɨɱɤɨɣ (x

) ɞɥɹ f(x, r) = 0 ɧɚɡɵɜɚɟɬɫɹ ɬɨɱɤɚ, ɜ ɤɨɬɨɪɨɣ ɥɢɛɨ

≠ 0, ɥɢɛɨ f

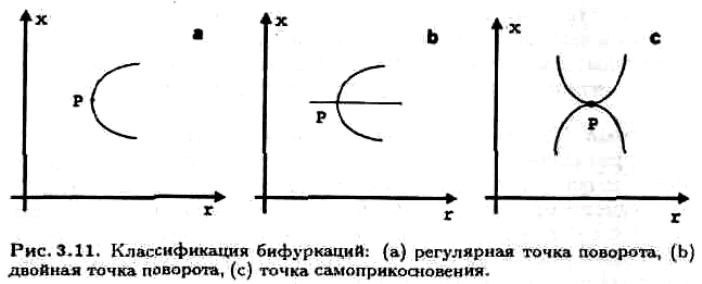
≠ 0. Ɋɟɝɭɥɹɪɧɨɣ ɬɨɱɤɨɣ ɩɨɜɨɪɨɬɚ ɧɚɡɵɜɚɟɬɫɹ ɬɚɤɚɹ ɪɟɝɭɥɹɪɧɚɹ

ɬɨɱɤɚ, ɜ ɤɨɬɨɪɨɣ r

(ɯ) ɢɡɦɟɧɹɟɬ ɡɧɚɤ. ɇɚ ɪɢɫ. 3.11a ɩɪɟɞɫɬɚɜɥɟɧ ɫɥɭɱɚɣ f

= 0

ɩɪɢ f

≠ 0 ɜ ɬɨɱɤɟ Ɋ.

ii Ɉɫɨɛɚɹ ɬɨɱɤɚ — ɷɬɨ ɧɟɪɟɝɭɥɹɪɧɚɹ ɬɨɱɤɚ ɫɨɫɬɨɹɧɢɹ ɪɚɜɧɨɜɟɫɢɹ, ɜ ɤɨɬɨɪɨɣ

= f

= 0.

iii

Ɍɨɱɤɨɣ ɛɢɮɭɪɤɚɰɢɢ ɧɚɡɵɜɚɟɬɫɹ ɬɚɤɚɹ ɨɫɨɛɚɹ ɬɨɱɤɚ, ɱɟɪɟɡ ɤɨɬɨɪɭɸ ɩɪɨɯɨɞɹɬ

ɞɜɟ ɢɥɢ ɛɨɥɟɟ ɜɟɬɜɟɣ ɪɟɲɟɧɢɹ ɭɪɚɜɧɟɧɢɹ f(x,r) = 0.

Ⱦɜɨɣɧɚɹ ɬɨɱɤɚ — ɷɬɨ ɬɚɤɚɹ ɨɫɨɛɚɹ ɬɨɱɤɚ, ɱɟɪɟɡ ɤɨɬɨɪɭɸ ɩɪɨɯɨɞɹɬ ɞɜɟ ɢ

ɬɨɥɶɤɨ ɞɜɟ ɜɟɬɜɢ ɪɟɲɟɧɢɹ ɭɪɚɜɧɟɧɢɹ f(x,r) = 0, ɢɦɟɸɳɢɟ ɪɚɡɧɵɟ

ɤɚɫɚɬɟɥɶɧɵɟ, ɩɪɢɱɟɦ ɜɫɟ ɜɬɨɪɵɟ ɩɪɨɢɡɜɨɞɧɵɟ ɨɬ f ɜ ɷɬɨɣ ɬɨɱɤɟ ɧɟ

ɨɛɪɚɳɚɸɬɫɹ ɜ ɧɭɥɶ ɨɞɧɨɜɪɟɦɟɧɧɨ. Ⱦɜɨɣɧɨɣ ɬɨɱɤɨɣ ɩɨɜɨɪɨɬɚ ɧɚɡɵɜɚɟɬɫɹ

ɞɜɨɣɧɚɹ ɬɨɱɤɚ, ɜ ɤɨɬɨɪɨɣ ɧɚ ɤɚɤɨɣ-ɥɢɛɨ ɢɡ ɜɟɬɜɟɣ ɩɪɨɢɡɜɨɞɧɚɹ r

ɢɡɦɟɧɹɟɬ

ɡɧɚɤ (ɪɢɫ. 3.11b).

Ɍɨɱɤɚ ɫɚɦɨɩɪɢɤɨɫɧɨɜɟɧɢɹ — ɷɬɨ ɬɨɱɤɚ ɫɨɩɪɢɤɨɫɧɨɜɟɧɢɹ ɜɬɨɪɨɝɨ ɩɨɪɹɞɤɚ

ɞɜɭɯ ɜɟɬɜɟɣ ɤɪɢɜɨɣ (ɪɢɫ. 3.11ɫ).

ɋɨɩɪɹɠɟɧɧɨɣ ɬɨɱɤɨɣ ɧɚɡɵɜɚɟɬɫɹ ɢɡɨɥɢɪɨɜɚɧɧɚɹ ɨɫɨɛɚɹ ɬɨɱɤɚ ɤɪɢɜɨɣ

f(x,r) = 0.

vii

Ɉɫɨɛɨɣ ɬɨɱɤɨɣ ɜɵɫɲɟɝɨ ɩɨɪɹɞɤɚ ɧɚɡɵɜɚɟɬɫɹ ɨɫɨɛɚɹ ɬɨɱɤɚ, ɜ ɤɨɬɨɪɨɣ ɜɫɟ ɬɪɢ

ɜɬɨɪɵɟ ɩɪɨɢɡɜɨɞɧɵɟ ɮɭɧɤɰɢɢ f(x, r) ɨɛɪɚɳɚɸɬɫɹ ɜ ɧɭɥɶ.

Ɍɟɨɪɢɹ ɛɢɮɭɪɤɚɰɢɣ ɢɡɭɱɚɟɬ ɜɨɩɪɨɫɵ ɫɭɳɟɫɬɜɨɜɚɧɢɹ ɢ ɭɫɬɨɣɱɢɜɨɫɬɢ

ɪɚɜɧɨɜɟɫɧɵɯ ɪɟɲɟɧɢɣ, ɬɚɤ ɤɚɤ ɜ ɪɟɚɥɶɧɨɣ ɫɢɬɭɚɰɢɢ ɧɟɭɫɬɨɣɱɢɜɵɯ ɪɚɜɧɨɜɟɫɧɵɯ

ɪɟɲɟɧɢɣ ɭɪɚɜɧɟɧɢɣ ɧɟ ɧɚɛɥɸɞɚɟɬɫɹ. ɋɤɚɠɟɦ ɡɞɟɫɶ ɟɳɟ, ɱɬɨ ɦɟɠɞɭ ɧɚɪɭɲɟɧɢɟɦ

ɭɫɬɨɣɱɢɜɨɫɬɢ ɢ ɛɢɮɭɪɤɚɰɢɟɣ ɫɭɳɟɫɬɜɭɟɬ ɬɟɫɧɚɹ ɫɜɹɡɶ. Ɂɚ ɛɨɥɟɟ ɫɬɪɨɝɢɦ

ɢɡɥɨɠɟɧɢɟɦ ɬɟɨɪɢɢ ɛɢɮɭɪɤɚɰɢɣ ɨɬɫɵɥɚɟɦ ɱɢɬɚɬɟɥɹ ɤ ɤɧɢɝɚɦ ɋɚɬɬɢɧɝɟɪɚ (1973),

Ƀɨɫɫɚ ɢ Ⱦɠɨɡɟɮɚ (1980) ɢɥɢ ɑɭ ɢ ɏɟɣɥɚ (1982)

. ɇɢɠɟ ɞɥɹ ɢɥɥɸɫɬɪɚɰɢɢ ɩɨɧɹɬɢɹ

ɛɢɮɭɪɤɚɰɢɢ ɩɪɢɜɟɞɟɦ ɧɟɫɤɨɥɶɤɨ ɩɪɢɦɟɪɨɜ.

ɋɦ. ɬɚɤɠɟ ɫɧɨɫɤɭ ɜ ɪɚɡɞ. 3.2. — ɉɪɢɦ. ɪɟɞ.

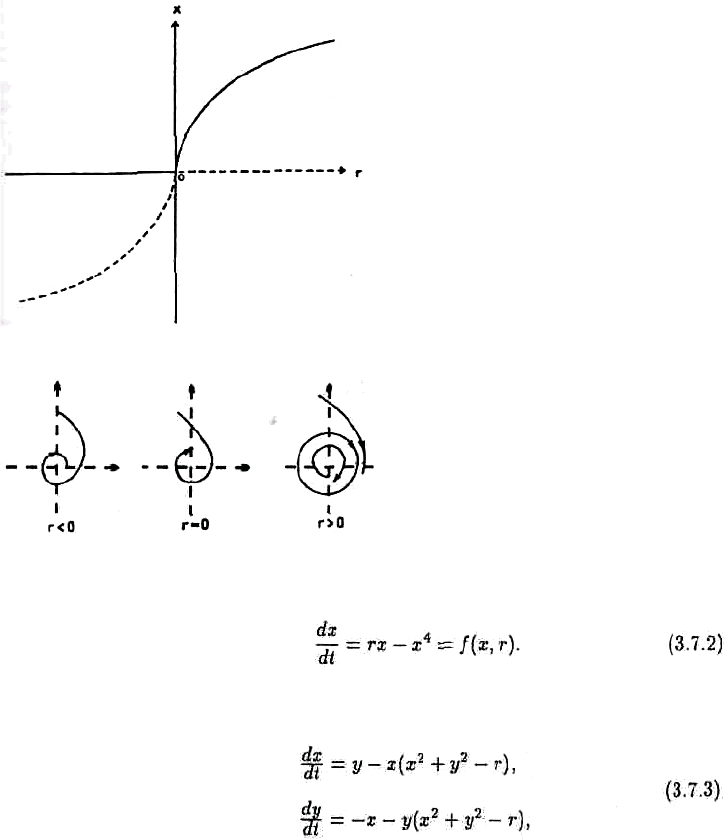
Ɋɢɫ. 3.12. Ȼɢɮɭɪɤɚɰɢɨɧɧɚɹ ɞɢɚɝɪɚɦɦɚ ɭɪɚɜɧɟɧɢɹ (3.7.2).

Ɋɢɫ. 3.13 Ȼɢɮɭɪɤɚɰɢɹ ɏɨɩɮɚ.

Ɋɚɫɫɦɨɬɪɢɦ ɭɪɚɜɧɟɧɢɟ

ȿɝɨ ɛɢɮɭɪɤɚɰɢɨɧɧɚɹ ɞɢɚɝɪɚɦɦɚ ɩɪɟɞɫɬɚɜɥɟɧɚ ɧɚ ɪɢɫ. 3.12, ɝɞɟ ɫɩɥɨɲɧɨɣ ɥɢɧɢɟɣ

ɨɛɨɡɧɚɱɟɧɚ ɭɫɬɨɣɱɢɜɚɹ ɜɟɬɜɶ, ɚ ɩɭɧɤɬɢɪɨɦ — ɧɟɭɫɬɨɣɱɢɜɚɹ.

Ⱦɥɹ ɭɪɚɜɧɟɧɢɣ

ɬɨɱɤɚ r = 0 ɹɜɥɹɟɬɫɹ ɬɨɱɤɨɣ ɛɢɮɭɪɤɚɰɢɢ ɮɚɡɨɜɨɝɨ ɩɨɬɨɤɚ (ɪɢɫ. 3.13). Ɉɬ

ɪɚɜɧɨɜɟɫɧɨɝɨ ɪɟɲɟɧɢɹ (0,0) ɨɬɜɟɬɜɥɹɟɬɫɹ ɩɟɪɢɨɞɢɱɟɫɤɚɹ ɨɪɛɢɬɚ x

+ ɭ

= r, ɩɪɢ ɷɬɨɦ

ɩɪɨɢɫɯɨɞɢɬ ɢɡɦɟɧɟɧɢɟ ɯɚɪɚɤɬɟɪɚ ɭɫɬɨɣɱɢɜɨɫɬɢ, ɤɚɤ ɩɨɤɚɡɚɧɨ ɧɚ ɪɢɫɭɧɤɟ. ɗɬɨɬ ɬɢɩ

ɛɢɮɭɪɤɚɰɢɢ

(

ɛɢɮɭɪɤɚɰɢɹ ɏɨɩɮɚ) ɹɜɥɹɟɬɫɹ ɫɥɟɞɫɬɜɢɟɦ ɩɪɨɹɜɥɟɧɢɹ ɞɢɧɚɦɢɱɟɫɤɢɯ ɫɜɨɣɫɬɜ

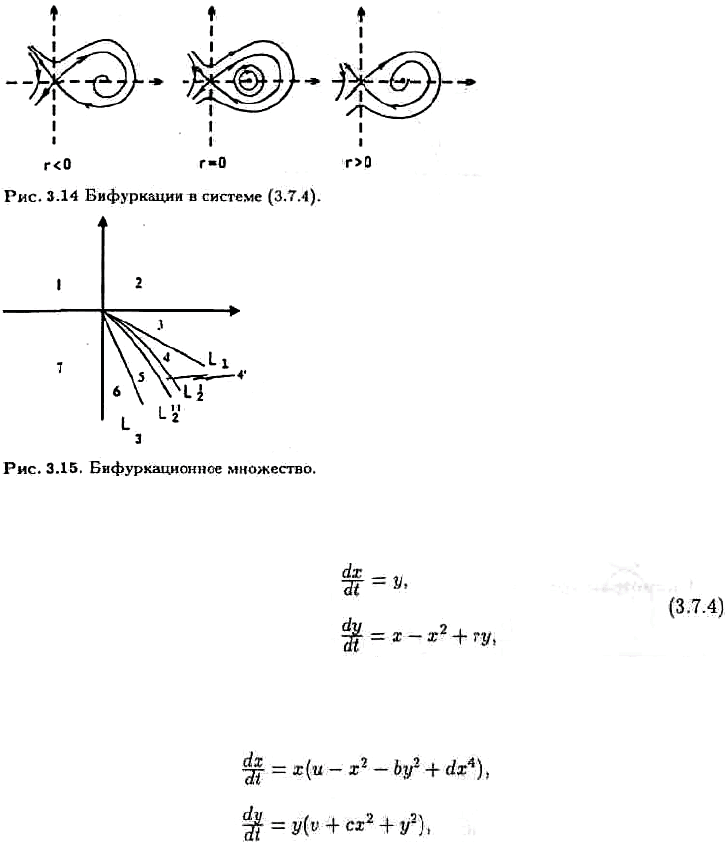
ɫɢɫɬɟɦɵ. Ⱦɥɹ ɭɪɚɜɧɟɧɢɣ

ɬɨɱɤɚ r = 0 ɹɜɥɹɟɬɫɹ ɬɨɱɤɨɣ ɛɢɮɭɪɤɚɰɢɢ ɫ ɬɪɚɟɤɬɨɪɢɹɦɢ, ɩɪɟɞɫɬɚɜɥɟɧɧɵɦɢ ɧɚ ɪɢɫ.

3.14 (

ɫɦ. ɑɭ ɢ ɏɟɣɥ, 1982). Ɍɨɱɤɚ ɪɚɜɧɨɜɟɫɢɹ (0,1) ɢɡɦɟɧɹɟɬ ɫɜɨɢ ɫɜɨɣɫɬɜɚ

ɭɫɬɨɣɱɢɜɨɫɬɢ ɩɪɢ ɩɟɪɟɯɨɞɟ r ɨɬ ɨɬɪɢɰɚɬɟɥɶɧɵɯ ɤ ɩɨɥɨɠɢɬɟɥɶɧɵɦ ɡɧɚɱɟɧɢɹɦ.

Ɋɚɫɫɦɨɬɪɢɦ ɭɪɚɜɧɟɧɢɹ

ɝɞɟ b > 0, ɫ > 0, bɫ > 1, d ≠ 0 — ɮɢɤɫɢɪɨɜɚɧɧɵɟ ɩɚɪɚɦɟɬɪɵ, ɚ ɢ ɢ v —

ɛɢɮɭɪɤɚɰɢɨɧɧɵɟ ɩɚɪɚɦɟɬɪɵ, ɢɡɦɟɧɹɸɳɢɟɫɹ ɜ ɨɤɪɟɫɬɧɨɫɬɢ ɧɭɥɹ. ɋɥɟɞɭɸɳɚɹ ɧɢɠɟ

ɬɟɨɪɟɦɚ ɞɚɟɬ ɩɨɥɧɨɟ ɨɩɢɫɚɧɢɟ ɛɢɮɭɪɤɚɰɢɣ, ɤɨɬɨɪɵɟ ɜɨɡɧɢɤɚɸɬ ɜ ɷɬɨɦ ɭɪɚɜɧɟɧɢɢ

(

ɫɦ. ɑɭ ɢ ɏɟɣɥ, 1982).

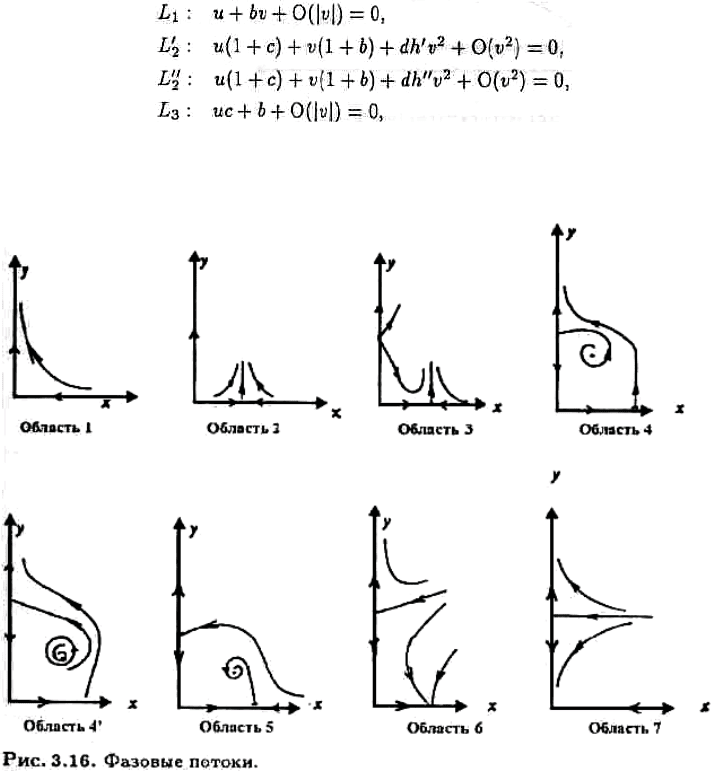
Ɍɟɨɪɟɦɚ 3.7.2. ɋɭɳɟɫɬɜɭɟɬ ɬɚɤɚɹ ɨɤɪɟɫɬɧɨɫɬɶ U ɬɨɱɤɢ (ɯ,ɭ) = (0,0) ɢ ɬɚɤɚɹ

ɨɤɪɟɫɬɧɨɫɬɶ V ɬɨɱɤɢ (u,v) = (0,0), ɱɬɨ ɩɪɢ ɜɵɞɟɥɟɧɢɢ ɜ ɨɤɪɟɫɬɧɨɫɬɢ V ɩɨɞɨɛɥɚɫɬɟɣ,

ɤɚɤ ɩɨɤɚɡɚɧɨ ɧɚ ɪɢɫ. 3.15, ɜ ɤɨɬɨɪɵɯ ɩɨɬɨɤ ɫɢɫɬɟɦɵ ɜ ɤɜɚɞɪɚɧɬɟ ɯ ≥ 0, ɭ ≥ 0 ɢɦɟɟɬ

ɜɢɞ, ɢɡɨɛɪɚɠɟɧɧɵɣ ɧɚ ɪɢɫ. 3.16, ɞɥɹ ɥɸɛɵɯ ɬɨɱɟɤ (ɢ, v) ɜ ɩɨɞɨɛɥɚɫɬɢ ɦɟɠɞɭ L'

ɢ L''

ɢɦɟɟɬɫɹ ɩɨ ɤɪɚɣɧɟɣ ɦɟɪɟ ɨɞɧɚ ɩɟɪɢɨɞɢɱɟɫɤɚɹ ɨɪɛɢɬɚ. Ʉɪɢɜɵɟ L

, L'

, L''

ɡɚɞɚɸɬɫɹ

ɮɨɪɦɭɥɚɦɢ

ɝɞɟ v ≤ 0, ɚ ɤɨɧɫɬɚɧɬɵ h' ɢ h" ɥɟɝɤɨ ɜɵɱɢɫɥɢɬɶ. Ʉɚɠɞɚɹ ɢɡ ɛɢɮɭɪɤɚɰɢɣ ɢɦɟɟɬ ɬɢɩ

ɫɟɞɥɨ-ɭɡɟɥ», ɡɚ ɢɫɤɥɸɱɟɧɢɟɦ ɬɟɯ, ɱɬɨ ɜɨɡɧɢɤɚɸɬ ɩɪɢ ɩɟɪɟɯɨɞɟ ɝɪɚɧɢɰ L'

ɢ L''

, ɝɞɟ

ɞɥɹ L''

ɢɦɟɟɦ ɛɢɮɭɪɤɚɰɢɸ ɏɨɩɮɚ, ɚ ɞɥɹ L'

— ɝɟɬɟɪɨɤɥɢɧɢɱɟɫɤɭɸ ɨɪɛɢɬɭ.

ɋɨɨɛɳɢɦ ɟɳɟ ɧɟɤɨɬɨɪɵɟ ɩɨɥɟɡɧɵɟ ɫɜɟɞɟɧɢɹ ɢɡ ɬɟɨɪɢɢ ɛɢɮɭɪɤɚɰɢɣ. Ɉɩɪɟɞɟɥɢɦ

ɤɚɫɤɚɞ ɛɢɮɭɪɤɚɰɢɣ ɤɚɤ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɫɬɶ ɛɢɮɭɪɤɚɰɢɣ ɪɟɲɟɧɢɣ ɧɟɥɢɧɟɣɧɵɯ

ɭɪɚɜɧɟɧɢɣ ɩɪɢ ɭɜɟɥɢɱɟɧɢɢ ɛɢɮɭɪɤɚɰɢɨɧɧɨɝɨ

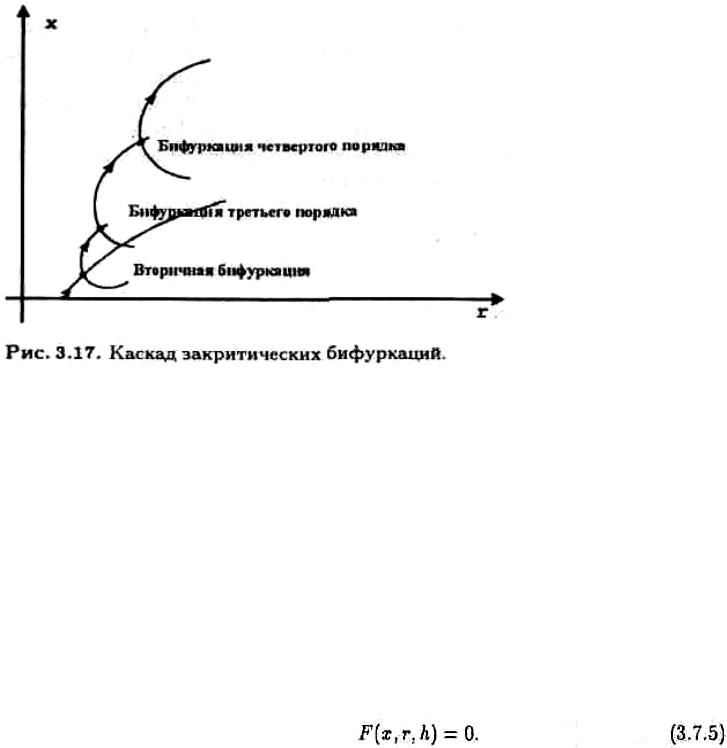
ɩɚɪɚɦɟɬɪɚ (ɪɢɫ. 3.17). Ʉɚɠɞɚɹ ɛɢɮɭɪɤɚɰɢɹ ɦɨɠɟɬ ɩɪɢɜɟɫɬɢ ɢ ɤ ɛɨɥɟɟ ɫɥɨɠɧɨɦɭ

ɩɨɜɟɞɟɧɢɸ, ɱɟɦ ɭɠɟ ɪɚɫɫɦɨɬɪɟɧɧɵɟ. ɉɪɢɦɟɪɨɦ ɦɨɠɟɬ ɩɨɫɥɭɠɢɬɶ, ɜ ɱɚɫɬɧɨɫɬɢ,

ɞɢɚɝɪɚɦɦɚ Ʌɚɧɞɚɭ-ɏɨɩɮɚ. ɋɰɟɧɚɪɢɣ ɬɚɤɨɜ: ɫɬɚɰɢɨɧɚɪɧɨɟ (ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɨ

ɨɞɧɨɪɨɞɧɨɟ) ɫɨɫɬɨɹɧɢɟ ɪɚɫɩɚɞɚɟɬɫɹ ɧɚ ɧɨɜɵɟ ɫɬɚɰɢɨɧɚɪɧɵɟ (ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɨ ɧɟ-

ɨɞɧɨɪɨɞɧɵɟ) ɫɨɫɬɨɹɧɢɹ. Ʉɚɠɞɨɟ ɧɨɜɨɟ ɛɢɮɭɪɰɢɪɭɟɬ ɞɚɥɟɟ ɤ ɫɨɫɬɨɹɧɢɸ

ɨɫɰɢɥɥɹɬɨɪɧɨɝɨ ɬɢɩɚ (ɛɢɮɭɪɤɚɰɢɹ ɏɨɩɮɚ). Ɂɚɬɟɦ ɩɪɟɞɟɥɶɧɵɣ ɰɢɤɥ ɛɢɮɭɪɰɢɪɭɟɬ ɤ

ɬɨɪɭ. Ʌɚɧɞɚɭ (1944) ɜɵɫɤɚɡɚɥ ɩɪɟɞɩɨɥɨɠɟɧɢɟ, ɱɬɨ ɷɬɢ ɬɢɩɵ ɩɟɪɟɯɨɞɨɜ

ɩɪɨɞɨɥɠɚɸɬɫɹ ɞɚɥɟɟ ɬɚɤɢɦ ɨɛɪɚɡɨɦ, ɱɬɨ ɫɢɫɬɟɦɚ ɢɫɩɵɬɵɜɚɟɬ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɵɟ

ɛɢɮɭɪɤɚɰɢɢ ɤ ɬɨɪɚɦ ɜɫɟ ɛɨɥɟɟ ɢ ɛɨɥɟɟ ɜɵɫɨɤɢɯ ɪɚɡɦɟɪɧɨɫɬɟɣ.

Ɇɨɠɧɨ ɭɬɜɟɪɠɞɚɬɶ, ɱɬɨ ɜ ɪɟɚɥɶɧɨɣ ɫɢɬɭɚɰɢɢ ɨɩɢɫɚɧɧɵɟ ɜɵɲɟ ɛɢɮɭɪɤɚɰɢɢ

ɧɚɛɥɸɞɚɸɬɫɹ ɪɟɞɤɨ, ɩɨɫɤɨɥɶɤɭ ɩɪɹɦɵɟ ɩɟɪɟɯɨɞɵ ɢ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɫɬɪɭɤɬɭɪɧɵɟ

ɢɡɦɟɧɟɧɢɹ ɫɝɥɚɠɢɜɚɸɬɫɹ ɜɫɟɝɞɚ ɩɪɢɫɭɬɫɬɜɭɸɳɢɦɢ ɧɚ ɩɪɚɤɬɢɤɟ ɞɟɮɟɤɬɚɦɢ ɢ

ɜɨɡɦɭɳɟɧɢɹɦɢ.

ȼ ɤɚɱɟɫɬɜɟ ɩɪɢɦɟɪɚ ɪɚɫɫɦɨɬɪɢɦ ɨɛɳɭɸ ɧɟɥɢɧɟɣɧɭɸ ɡɚɞɚɱɭ

Ɋɟɲɟɧɢɟ ɯ = x(r, h) ɡɚɜɢɫɢɬ ɨɬ ɞɜɭɯ ɫɤɚɥɹɪɧɵɯ ɩɚɪɚɦɟɬɪɨɜ r ɢ h. ɉɚɪɚɦɟɬɪ r,

ɧɚɡɵɜɚɟɦɵɣ ɛɢɮɭɪɤɚɰɢɨɧɧɵɦ ɩɚɪɚɦɟɬɪɨɦ, ɹɜɥɹɟɬɫɹ «ɜɯɨɞɧɨɣ ɚɦɩɥɢɬɭɞɨɣ»

ɫɢɫɬɟɦɵ (3.7.5), ɚ ɦɚɥɵɣ ɩɚɪɚɦɟɬɪ h — ɚɦɩɥɢɬɭɞɨɣ ɧɟɨɩɪɟɞɟɥɟɧɧɨɫɬɢ. ȿɫɥɢ h = 0,

ɢɫɫɥɟɞɨɜɚɧɢɟ F(x, r, 0) ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɛɢɮɭɪɤɚɰɢɨɧɧɭɸ ɡɚɞɚɱɭ. ȿɫɥɢ h ɧɟ

ɪɚɜɧɨ ɧɭɥɸ, ɧɚɡɨɜɟɦ (3.7.5) ɜɨɡɦɭɳɟɧɧɨɣ ɢɥɢ ɧɟɨɩɪɟɞɟɥɟɧɧɨɣ ɛɢɮɭɪɤɚɰɢɨɧɧɨɣ

ɡɚɞɚɱɟɣ.

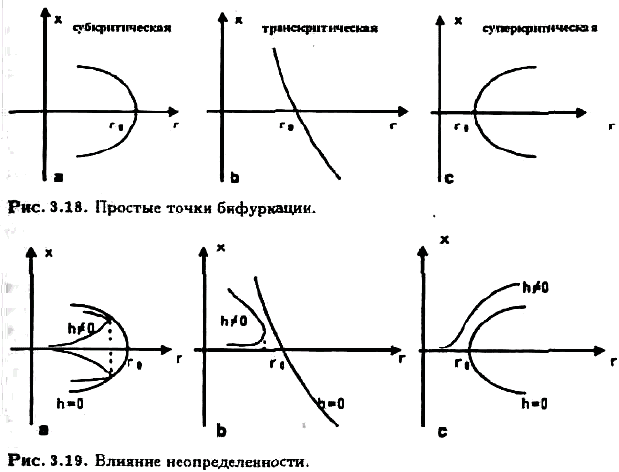
Ɋɚɫɫɦɨɬɪɢɦ ɫɥɭɱɚɣ, ɤɨɝɞɚ h = 0, ɢ r — ɬɨɱɤɚ ɛɢɮɭɪɤɚɰɢɢ ɮɭɧɤɰɢɢ F(x, r, 0). ɇɚ

ɪɢɫ. 3.18 ɩɨɤɚɡɚɧɵ ɬɪɢ ɬɢɩɚ ɛɢɮɭɪɤɚɰɢɣ, ɤɨɬɨɪɵɟ ɜɨɡɧɢɤɚɸɬ ɜɛɥɢɡɢ ɩɪɨɫɬɨɣ ɬɨɱɤɢ

ɛɢɮɭɪɤɚɰɢɢ r = r

. Ɍɢɩɢɱɧɵɟ ɞɢɚɝɪɚɦɦɵ ɨɬɤɥɢɤɚ ɪɟɲɟɧɢɣ ɧɟɨɩɪɟɞɟɥɟɧɧɨɣ

ɛɢɮɭɪɤɚɰɢɨɧɧɨɣ ɡɚɞɚɱɢ ɫɨɛɪɚɧɵ ɧɚ ɪɢɫ. 3.19. ɉɨ ɚɧɚɥɨɝɢɢ ɫ r

ɨɩɪɟɞɟɥɹɟɬɫɹ ɧɨɜɵɣ

ɤɪɢɬɢɱɟɫɤɢɣ ɩɚɪɚɦɟɬɪ r = r

< r

. Ɍɨɱɤɚ r

ɧɚɡɵɜɚɟɬɫɹ ɩɪɟɞɟɥɶɧɨɣ.

3.8 Ɍɟɨɪɢɹ ɨɫɨɛɟɧɧɨɫɬɟɣ

Ɇɧɨɝɢɟ ɷɤɨɧɨɦɢɱɟɫɤɢɟ ɩɪɨɛɥɟɦɵ ɫɜɨɞɹɬɫɹ ɤ ɢɫɫɥɟɞɨɜɚɧɢɸ ɫɜɨɣɫɬɜ ɝɥɚɞɤɢɯ

ɮɭɧɤɰɢɣ. ɇɚɩɪɢɦɟɪ, ɪɚɰɢɨɧɚɥɶɧɨɟ ɩɨɜɟɞɟɧɢɟ ɩɪɟɞɩɪɢɧɢɦɚɬɟɥɹ ɢɥɢ ɞɨɦɨɯɨɡɹɢɧɚ ɜ

ɭɫɥɨɜɢɹɯ ɢɞɟɚɥɶɧɨɝɨ ɪɵɧɤɚ ɦɨɠɧɨ ɨɩɢɫɚɬɶ ɮɭɧɤɰɢɹɦɢ, ɡɚɜɢɫɹɳɢɦɢ ɨɬ ɰɟɧ.

ɉɪɢɦɟɧɹɹ ɬɟɨɪɢɸ ɫɪɚɜɧɢɬɟɥɶɧɨɣ ɫɬɚɬɢɤɢ, ɦɨɠɧɨ ɢɫɫɥɟɞɨɜɚɬɶ, ɤɚɤ ɢɡɦɟɧɢɬɫɹ ɫɩɪɨɫ

ɢɥɢ ɩɪɟɞɥɨɠɟɧɢɟ ɩɪɢ ɢɡɦɟɧɟɧɢɢ ɪɵɧɨɱɧɵɯ ɰɟɧ. Ɉɫɧɨɜɧɭɸ ɪɨɥɶ ɩɪɢ ɢɫɫɥɟɞɨɜɚɧɢɢ

ɩɨɜɟɞɟɧɢɹ ɦɟɥɤɨɝɨ ɩɪɨɢɡɜɨɞɢɬɟɥɹ ɢ ɩɨɬɪɟɛɢɬɟɥɹ ɢɝɪɚɸɬ ɩɪɨɢɡɜɨɞɫɬɜɟɧɧɵɟ

ɮɭɧɤɰɢɢ ɢ ɮɭɧɤɰɢɢ ɩɨɥɟɡɧɨɫɬɢ. Ɍɟɨɪɢɹ ɨɫɨɛɟɧɧɨɫɬɟɣ ɡɚɧɢɦɚɟɬɫɹ ɤɥɚɫɫɢɮɢɤɚɰɢɟɣ

ɢ ɢɡɭɱɟɧɢɟɦ ɝɥɚɞɤɢɯ ɮɭɧɤɰɢɣ. ɗɬɚ ɬɟɨɪɢɹ ɢɦɟɟɬ ɫɭɳɟɫɬɜɟɧɧɵɟ ɞɨɫɬɢɠɟɧɢɹ. Ɍɟɨɪɢɹ

ɤɚɬɚɫɬɪɨɮ — ɨɞɧɨ ɢɡ ɧɚɢɛɨɥɟɟ ɜɚɠɧɵɯ ɧɚɩɪɚɜɥɟɧɢɣ ɜ ɫɨɜɪɟɦɟɧɧɨɣ ɩɪɢɤɥɚɞɧɨɣ

ɦɚɬɟɦɚɬɢɤɟ — ɹɜɥɹɟɬɫɹ ɟɟ ɱɚɫɬɧɵɦ ɫɥɭɱɚɟɦ.

Ɋɚɫɫɦɨɬɪɢɦ ɝɥɚɞɤɭɸ ɮɭɧɤɰɢɸ f : R

ĺR

ɢ ɩɪɟɞɩɨɥɨɠɢɦ, ɱɬɨ ɜ ɧɚɱɚɥɟ

ɤɨɨɪɞɢɧɚɬ f ɢɦɟɟɬ ɤɪɢɬɢɱɟɫɤɭɸ ɬɨɱɤɭ ɜ ɧɚɱɚɥɟ ɤɨɨɪɞɢɧɚɬ, ɬ.ɟ. Df(0) = 0. Ɍɟɨɪɢɹ

ɨɫɨɛɟɧɧɨɫɬɟɣ ɢɡɭɱɚɟɬ ɫɥɟɞɭɸɳɢɟ ɜɨɩɪɨɫɵ:

1. ɉɪɨɛɥɟɦɭ ɨɩɪɟɞɟɥɟɧɧɨɫɬɢ: ɤɚɤɨɜ ɥɨɤɚɥɶɧɵɣ ɯɚɪɚɤɬɟɪ ɮɭɧɤɰɢɢ f ɜ ɨɤɪɟɫɬɧɨɫɬɢ

ɧɭɥɹ? Ɏɚɤɬɢɱɟɫɤɢ ɷɬɨɬ ɜɨɩɪɨɫ ɷɤɜɢɜɚɥɟɧɬɟɧ ɜɨɩɪɨɫɭ: «ȼ ɤɚɤɨɣ ɬɨɱɤɟ ɦɨɠɧɨ

ɛɟɡ ɨɩɚɫɟɧɢɣ ɨɛɪɵɜɚɬɶ ɪɹɞ Ɍɟɣɥɨɪɚ ɮɭɧɤɰɢɢ f?»

ɉɪɨɛɥɟɦɭ ɪɚɡɜɟɪɬɤɢ: ɤɚɤɨɜɵ ɫɭɳɟɫɬɜɟɧɧɵɟ ɜɨɡɦɭɳɟɧɢɹ ɮɭɧɤɰɢɢ f? Ɍɨ ɟɫɬɶ,

ɤɚɤɢɟ ɜɨɡɦɭɳɟɧɢɹ ɮɭɧɤɰɢɢ f ɢɡɦɟɧɹɸɬ ɟɟ ɤɚɱɟɫɬɜɟɧɧɭɸ ɩɪɢɪɨɞɭ ɢ ɧɟ ɦɨɝɭɬ

ɛɵɬɶ ɭɫɬɪɚɧɟɧɵ ɡɚɦɟɧɨɣ ɩɟɪɟɦɟɧɧɵɯ?

ɉɪɨɛɥɟɦɭ ɤɥɚɫɫɢɮɢɤɚɰɢɢ: ɦɨɠɧɨ ɥɢ ɩɪɨɜɟɫɬɢ ɤɥɚɫɫɢɮɢɤɚɰɢɸ ɬɢɩɨɜ

ɨɫɨɛɟɧɧɨɫɬɟɣ ɮɭɧɤɰɢɢ f?

ɗɥɟɦɟɧɬɚɪɧɚɹ ɬɟɨɪɢɹ ɤɚɬɚɫɬɪɨɮ ɪɟɲɚɟɬ ɷɬɢ ɩɪɨɛɥɟɦɵ ɞɥɹ ɬ = 1. ȿɟ ɨɛɨɛɳɟɧɢɟ

—

ɬɟɨɪɢɹ ɨɫɨɛɟɧɧɨɫɬɟɣ — ɪɟɲɚɟɬ ɩɟɪɜɵɟ ɞɜɟ ɩɪɨɛɥɟɦɵ ɢ ɞɚɟɬ ɨɬɧɨɫɢɬɟɥɶɧɨ

ɩɨɥɧɭɸ ɢɧɮɨɪɦɚɰɢɸ ɨ ɬɪɟɬɶɟɣ ɞɥɹ ɦɚɥɵɯ ɩɢɬ.

ɑɬɨɛɵ ɩɪɨɢɥɥɸɫɬɪɢɪɨɜɚɬɶ ɩɪɢɦɟɧɟɧɢɟ ɬɟɨɪɢɢ ɨɫɨɛɟɧɧɨɫɬɟɣ, ɜɨɫɩɨɥɶɡɭɟɦɫɹ

ɩɪɢɦɟɪɨɦ: ɨɛɫɭɞɢɦ ɫ ɬɨɱɤɢ ɡɪɟɧɢɹ ɬɟɨɪɢɢ ɨɫɨɛɟɧɧɨɫɬɟɣ ɛɢɮɭɪɤɚɰɢɸ «ɩɢɬɱɮɨɪɤ»

—

ɛɢɮɭɪɤɚɰɢɸ ɬɢɩɚ ɜɢɥɤɢ (ɷɬɨɬ ɩɪɢɦɟɪ ɞɟɬɚɥɶɧɨ ɪɚɡɨɛɪɚɧ ɜ ɤɧɢɝɟ Ƚɨɥɭɛɢɰɤɨɝɨ ɢ

ɒɟɮɮɟɪɚ, 1984).

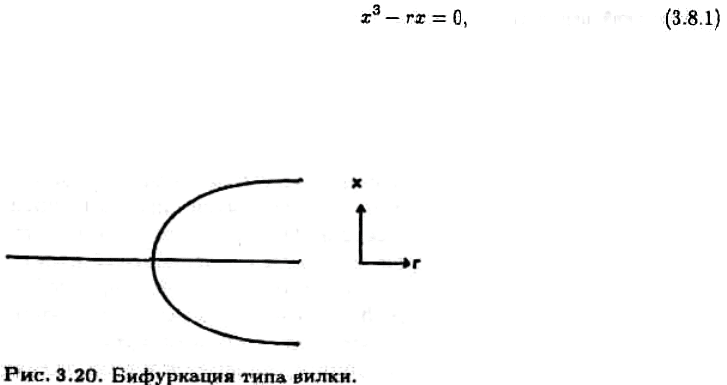
Ɋɚɫɫɦɨɬɪɢɦ ɭɪɚɜɧɟɧɢɟ

ɝɞɟ r — ɩɚɪɚɦɟɬɪ. Ɏɭɧɞɚɦɟɧɬɚɥɶɧɵɦ ɫɜɨɣɫɬɜɨɦ ɷɬɨɝɨ ɭɪɚɜɧɟɧɢɹ ɹɜɥɹɟɬɫɹ ɧɚɥɢɱɢɟ

ɛɢɮɭɪɤɚɰɢɢ ɬɢɩɚ ɜɢɥɤɢ, ɬ. ɟ. ɩɪɢ ɩɟɪɟɯɨɞɟ ɩɚɪɚɦɟɬɪɨɦ r ɧɟɤɨɬɨɪɨɣ ɜɟɥɢɱɢɧɵ

(= 0) ɱɢɫɥɨ ɪɟɲɟɧɢɣ ɩ(r) ɫɤɚɱɤɨɨɛɪɚɡɧɨ ɜɨɡɪɚɫɬɚɟɬ ɨɬ ɨɞɧɨɝɨ ɞɨ ɬɪɟɯ. Ɇɧɨɠɟɫɬɜɨ

ɪɟɲɟɧɢɣ (3.8.1) ɩɨɤɚɡɚɧɨ ɧɚ ɪɢɫ. 3.20.

Ʉɚɤ ɭɠɟ ɝɨɜɨɪɢɥɨɫɶ, ɩɪɢ ɩɪɢɦɟɧɟɧɢɢ ɬɟɨɪɢɢ ɨɫɨɛɟɧɧɨɫɬɟɣ ɤ ɚɧɚɥɢɡɭ

ɛɢɮɭɪɤɚɰɢɣ ɜɨɡɧɢɤɚɸɬ ɞɜɚ ɫɥɨɠɧɵɯ ɜɨɩɪɨɫɚ. ɉɟɪɜɵɣ ɨɬɧɨɫɢɬɫɹ ɤ ɫɬɟɩɟɧɢ

ɜɚɠɧɨɫɬɢ ɜɤɥɚɞɚ ɱɥɟɧɨɜ ɜɵɫɲɢɯ ɩɨɪɹɞɤɨɜ. ɂɧɵɦɢ ɫɥɨɜɚɦɢ, ɜɨɩɪɨɫ ɦɨɠɧɨ

ɫɮɨɪɦɭɥɢɪɨɜɚɬɶ ɬɚɤ: ɞɨ ɤɚɤɢɯ ɩɨɪ

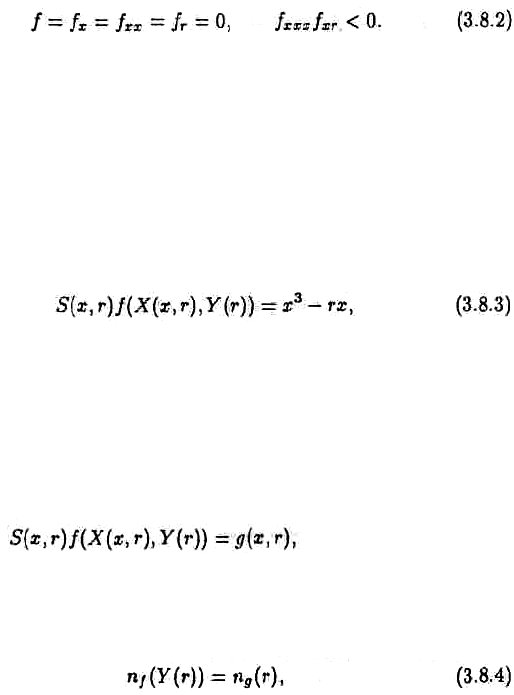
ɤɚɱɟɫɬɜɟɧɧɨɟ ɩɨɜɟɞɟɧɢɟ ɮɭɧɤɰɢɢ f(x, r) ɜ ɨɤɪɟɫɬɧɨɫɬɢ ɛɢɮɭɪɤɚɰɢɢ ɨɩɪɟɞɟɥɹɟɬɫɹ

ɱɥɟɧɚɦɢ ɧɢɡɲɢɯ ɩɨɪɹɞɤɨɜ ɪɚɡɥɨɠɟɧɢɹ ɮɭɧɤɰɢɢ ɜ ɪɹɞ Ɍɟɣɥɨɪɚ, ɩɨɡɜɨɥɹɹ

ɩɪɟɧɟɛɪɟɝɚɬɶ ɜɨɡɦɨɠɧɵɦ ɜɥɢɹɧɢɟɦ ɱɥɟɧɨɜ ɜɵɫɲɢɯ ɩɨɪɹɞɤɨɜ? ɉɭɫɬɶ ɜ ɫɥɭɱɚɟ

ɛɢɮɭɪɤɚɰɢɢ ɬɢɩɚ ɜɢɥɤɢ ɞɥɹ f(x, r) ɩɪɢ (x, r) = (ɯ

, r

) ɢɦɟɟɦ

Ɉɱɟɜɢɞɧɨ, (3.8.1) ɭɞɨɜɥɟɬɜɨɪɹɟɬ ɷɬɨɦɭ ɬɪɟɛɨɜɚɧɢɸ. ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɡɧɚɱɟɧɢɟ ɩ(r),

ɱɢɫɥɨ ɪɟɲɟɧɢɣ f(x, r), ɫɤɚɱɤɨɦ ɜɨɡɪɚɫɬɚɟɬ ɨɬ ɨɞɧɨɝɨ ɞɨ ɬɪɟɯ ɩɪɢ ɩɟɪɟɯɨɞɟ r ɱɟɪɟɡ

ɩɨɪɨɝɨɜɨɟ ɡɧɚɱɟɧɢɟ r

. ɗɬɨ ɦɨɠɧɨ ɞɨɤɚɡɚɬɶ, ɜɨɫɩɨɥɶɡɨɜɚɜɲɢɫɶ ɬɟɨɪɟɦɨɣ ɨ ɧɟɹɜɧɨɣ

ɮɭɧɤɰɢɢ. Ɉɞɧɚɤɨ ɜ ɬɟɨɪɢɢ ɨɫɨɛɟɧɧɨɫɬɟɣ ɞɨɤɚɡɚɧɨ ɡɧɚɱɢɬɟɥɶɧɨ ɛɨɥɟɟ ɫɢɥɶɧɨɟ

ɭɬɜɟɪɠɞɟɧɢɟ. Ɇɨɠɧɨ ɩɨɤɚɡɚɬɶ, ɱɬɨ ɥɸɛɚɹ ɮɭɧɤɰɢɹ f, ɭɞɨɜɥɟɬɜɨɪɹɸɳɚɹ (3.8.2),

ɦɨɠɟɬ ɛɵɬɶ ɩɪɢɜɟɞɟɧɚ ɤ ɫɬɚɧɞɚɪɬɧɨɣ ɦɨɞɟɥɢ ɛɢɮɭɪɤɚɰɢɢ-ɜɢɥɤɢ ɯ

— rɯ = 0

ɩɨɞɯɨɞɹɳɟɣ ɡɚɦɟɧɨɣ ɤɨɨɪɞɢɧɚɬ. Ɍɨɱɧɟɟ, ɟɫɥɢ f ɭɞɨɜɥɟɬɜɨɪɹɟɬ (3.8.2), ɬɨ

ɫɭɳɟɫɬɜɭɸɬ: (I) ɥɨɤɚɥɶɧɵɣ ɞɢɮɮɟɨɦɨɪɮɢɡɦ R

ɜɢɞɚ (x, r) ĺ (ɏ(ɯ, r), Y(r)),

ɨɬɨɛɪɚɠɚɸɳɢɣ ɧɚɱɚɥɨ ɤɨɨɪɞɢɧɚɬ ɜ ɬɨɱɤɭ (ɯ

, r

), ɢ (II) ɧɟɧɭɥɟɜɚɹ ɮɭɧɤɰɢɹ S(x, r),

ɬɚɤɚɹ, ɱɬɨ ɜ ɨɤɪɟɫɬɧɨɫɬɢ ɧɭɥɹ ɢɦɟɟɬ ɦɟɫɬɨ

ɝɞɟ ɏ

(ɯ, r) > 0 ɢ Y′ > 0. ɉɨɫɤɨɥɶɤɭ S ɧɟ ɨɛɪɚɳɚɟɬɫɹ ɜ ɧɭɥɶ, ɪɟɲɟɧɢɹ ɭɪɚɜɧɟɧɢɹ

f (ɯ, r) = 0 ɨɬɥɢɱɚɸɬɫɹ ɨɬ ɪɟɲɟɧɢɣ x

– rɯ = 0 ɫ ɬɨɱɧɨɫɬɶɸ ɞɨ ɞɢɮɮɟɨɦɨɪɮɢɡɦɚ. ɗɬɨ

ɨɡɧɚɱɚɟɬ, ɱɬɨ ɱɥɟɧɵ ɜɵɫɲɟɝɨ ɩɨɪɹɞɤɚ ɜ ɪɚɡɥɨɠɟɧɢɢ f ɧɟ ɜɥɢɹɸɬ ɧɚ ɤɚɱɟɫɬɜɟɧɧɨɟ

ɩɨɜɟɞɟɧɢɟ ɦɨɞɟɥɢ ɜ ɦɚɥɨɦ — ɨɧɢ ɦɨɝɭɬ ɛɵɬɶ ɭɧɢɱɬɨɠɟɧɵ ɩɨɞɯɨɞɹɳɟɣ ɡɚɦɟɧɨɣ

ɤɨɨɪɞɢɧɚɬ.

ɍɪɚɜɧɟɧɢɟ (3.8.3) ɩɪɢɜɨɞɢɬ ɧɚɫ ɤ ɨɩɪɟɞɟɥɟɧɢɸ ɮɭɧɞɚɦɟɧɬɚɥɶɧɨɝɨ ɩɨɧɹɬɢɹ

ɬɟɨɪɢɢ ɨɫɨɛɟɧɧɨɫɬɟɣ — ɩɨɧɹɬɢɹ ɷɤɜɢɜɚɥɟɧɬɧɨɫɬɢ. Ⱦɜɟ ɛɢɮɭɪɤɚɰɢɨɧɧɵɟ ɡɚɞɚɱɢ f ɢ J

ɷɤɜɢɜɚɥɟɧɬɧɵ, ɟɫɥɢ ɨɧɢ ɦɨɝɭɬ ɛɵɬɶ ɫɜɹɡɚɧɵ ɫɨɨɬɧɨɲɟɧɢɟɦ

ɝɞɟ S ɧɟ ɪɚɜɧɚ ɧɭɥɸ ɢ ɩɨɥɨɠɢɬɟɥɶɧɚ, ɚ (X, Y) — ɥɨɤɚɥɶɧɵɣ ɞɢɮɮɟɨɦɨɪɮɢɡɦ,

ɫɨɯɪɚɧɹɸɳɢɣ ɨɪɢɟɧɬɚɰɢɸ x ɢ r.

ȿɫɥɢ f ɢ J ɷɤɜɢɜɚɥɟɧɬɧɵ, ɬɨ ɬɚɤɢɟ ɞɜɟ ɧɟɨɞɧɨɡɧɚɱɧɵɟ ɮɭɧɤɰɢɢ ɫɜɹɡɚɧɵ

ɫɨɨɬɧɨɲɟɧɢɟɦ

ɱɬɨ ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɨɞɧɨ ɢɡ ɜɚɠɧɟɣɲɢɯ ɫɥɟɞɫɬɜɢɣ ɢɯ ɷɤɜɢɜɚɥɟɧɬɧɨɫɬɢ..

ɂɫɫɥɟɞɨɜɚɧɢɟ ɛɢɮɭɪɤɚɰɢɢ ɬɢɩɚ ɜɢɥɤɢ ɹɜɥɹɟɬɫɹ ɯɚɪɚɤɬɟɪɧɵɦ ɞɥɹ ɨɛɳɟɝɨ

ɩɨɞɯɨɞɚ ɬɟɨɪɢɢ ɨɫɨɛɟɧɧɨɫɬɟɣ ɤ ɩɪɨɛɥɟɦɟ ɨɩɪɟɞɟɥɟɧɧɨɫɬɢ. Ⱦɚɥɟɟ ɛɭɞɟɦ ɧɚɡɵɜɚɬɶ

– rɯ = 0 ɧɨɪɦɚɥɶɧɨɣ ɮɨɪɦɨɣ ɛɢɮɭɪɤɚɰɢɢ ɬɢɩɚ ɜɢɥɤɢ. ȼɫɹɤɚɹ ɛɢɮɭɪɤɚɰɢɨɧɧɚɹ

ɡɚɞɚɱɚ f(x, r), ɤɨɬɨɪɚɹ ɜ ɧɟɤɨɬɨɪɨɣ ɬɨɱɤɟ (ɯ

, r

) ɭɞɨɜɥɟɬɜɨɪɹɟɬ ɭɫɥɨɜɢɹɦ

ɷɤɜɢɜɚɥɟɧɬɧɚ ɷɬɨɣ ɧɨɪɦɚɥɶɧɨɣ ɮɨɪɦɟ. Ȼɭɞɟɦ ɝɨɜɨɪɢɬɶ, ɱɬɨ ɭɫɥɨɜɢɟ (3.8.5)

ɪɚɡɪɟɲɚɟɬ ɡɚɞɚɱɭ ɢɞɟɧɬɢɮɢɤɚɰɢɢ ɞɥɹ ɞɚɧɧɨɣ ɧɨɪɦɚɥɶɧɨɣ ɮɨɪɦɵ. ɗɤɜɢɜɚɥɟɧɬɧɵɟ

ɛɢɮɭɪɤɚɰɢɨɧɧɵɟ ɡɚɞɚɱɢ ɨɛɥɚɞɚɸɬ ɨɞɢɧɚɤɨɜɵɦɢ ɤɚɱɟɫɬɜɟɧɧɵɦɢ ɫɜɨɣɫɬɜɚɦɢ; ɬɨɱɧɟɟ

ɝɨɜɨɪɹ, ɤɚɱɟɫɬɜɟɧɧɵɟ ɫɜɨɣɫɬɜɚ — ɷɬɨ ɬɟ, ɤɨɬɨɪɵɟ ɩɪɢ ɧɚɥɢɱɢɢ ɷɤɜɢɜɚɥɟɧɬɧɨɫɬɢ ɫɨ-

ɯɪɚɧɹɸɬɫɹ.

ȼɬɨɪɵɦ ɫɥɨɠɧɵɦ ɜɨɩɪɨɫɨɦ ɹɜɥɹɟɬɫɹ ɜɨɩɪɨɫ, ɤɨɬɨɪɵɣ ɜɨɡɧɢɤɚɟɬ ɩɪɢ ɢɡɭɱɟɧɢɢ

ɬɨɝɨ, ɤɚɤ ɦɨɝɭɬ ɡɚɜɢɫɟɬɶ ɛɢɮɭɪɤɚɰɢɨɧɧɵɟ ɡɚɞɚɱɢ ɨɬ ɩɚɪɚɦɟɬɪɨɜ — ɜɟɞɶ ɦɚɥɵɟ

ɢɡɦɟɧɟɧɢɹ ɜɫɩɨɦɨɝɚɬɟɥɶɧɵɯ ɩɚɪɚɦɟɬɪɨɜ ɛɢɮɭɪɤɚɰɢɨɧɧɨɣ ɡɚɞɚɱɢ f (ɯ, r) ɜ ɨɫɨɛɨɣ

ɬɨɱɤɟ ɮɭɧɤɰɢɢ f ɩɪɢɜɨɞɹɬ, ɤɚɤ ɩɪɚɜɢɥɨ, ɤ ɤɚɱɟɫɬɜɟɧɧɵɦ ɢɡɦɟɧɟɧɢɹɦ

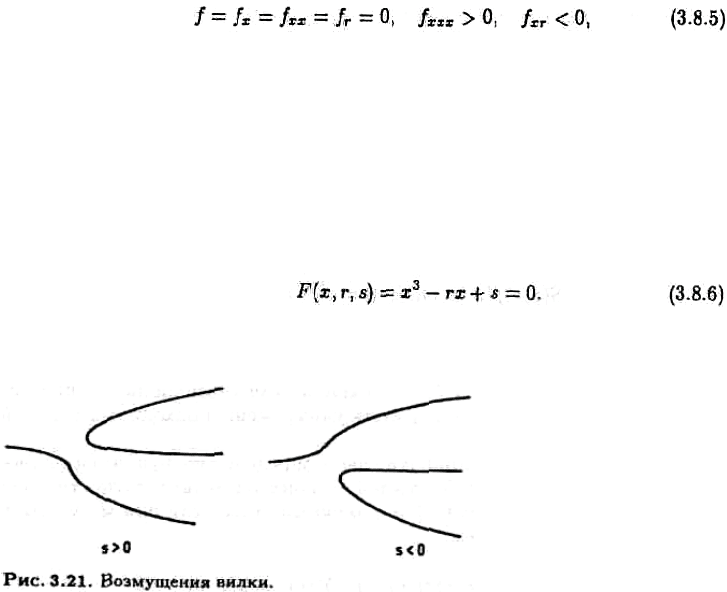
ɛɢɮɭɪɤɚɰɢɨɧɧɨɣ ɞɢɚɝɪɚɦɦɵ. Ɋɚɫɫɦɨɬɪɢɦ ɜɨɡɦɭɳɟɧɢɟ ɛɢɮɭɪɤɚɰɢɢ ɬɢɩɚ ɜɢɥɤɢ:

ɋɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɛɢɮɭɪɤɚɰɢɨɧɧɵɟ ɞɢɚɝɪɚɦɦɵ ɞɥɹ ɫɥɭɱɚɹ s ≠ 0 ɩɪɟɞɫɬɚɜɥɟɧɵ ɧɚ

ɪɢɫ. 3.21.

ȼ ɤɥɚɫɫɢɱɟɫɤɨɣ ɥɢɬɟɪɚɬɭɪɟ ɪɚɡɥɢɱɚɸɬ ɞɜɚ ɢɫɬɨɱɧɢɤɚ ɩɨɹɜɥɟɧɢɹ ɞɨɩɨɥɧɢɬɟɥɶɧɵɯ

ɩɚɪɚɦɟɬɪɨɜ ɛɢɮɭɪɤɚɰɢɨɧɧɨɣ ɡɚɞɚɱɢ. ȼɨ-ɩɟɪɜɵɯ, ɫɚɦɚ ɢɫɯɨɞɧɚɹ ɮɨɪɦɭɥɢɪɨɜɤɚ

ɷɤɨɧɨɦɢɱɟɫɤɨɣ ɦɨɞɟɥɢ ɦɨɠɟɬ ɫɨɞɟɪɠɚɬɶ ɦɧɨɠɟɫɬɜɨ ɜɫɩɨɦɨɝɚɬɟɥɶɧɵɯ ɩɚɪɚɦɟɬɪɨɜ.

ȼɨ-ɜɬɨɪɵɯ, ɧɨɜɵɟ ɩɚɪɚɦɟɬɪɵ ɜɨɡɧɢɤɚɸɬ ɩɪɢ ɭɬɨɱɧɟɧɢɢ ɛɨɥɟɟ ɝɪɭɛɨɣ ɦɨɞɟɥɢ. ȼ

ɩɨɞɯɨɞɟ, ɪɚɡɜɢɜɚɟɦɨɦ ɬɟɨɪɢɟɣ ɨɫɨɛɟɧɧɨɫɬɟɣ, ɜɨɡɧɢɤɧɨɜɟɧɢɟ ɞɨɩɨɥɧɢɬɟɥɶɧɵɯ

ɩɚɪɚɦɟɬɪɨɜ ɩɪɨɢɫɯɨɞɢɬ ɫɥɟɞɭɸɳɢɦ ɨɛɪɚɡɨɦ. ɋɩɟɪɜɚ ɞɥɹ ɞɚɧɧɨɣ ɛɢɮɭɪɤɚɰɢɨɧɧɨɣ

ɡɚɞɚɱɢ f ɫɬɪɨɢɬɫɹ ɨɩɪɟɞɟɥɟɧɧɨɟ ɯɚɪɚɤɬɟɪɧɨɟ ɫɟɦɟɣɫɬɜɨ ɜɨɡɦɭɳɟɧɢɣ f. ɉɭɫɬɶ

F(ɯ, r, s

,..., s

) ɢɥɢ ɩɪɨɫɬɨ