Зазуляк П.М., Гавриш В.І. Євсєєва Е.М., Йосипчук М.Д. Основи математичного опрацювання геодезичних вимірювань

Подождите немного. Документ загружается.

Елементи теорії ймовірностей

І нарешті, за формулою (2.31) знаходимо

Р(Д)

Л.І

І.І

І.«, 0,56

З 10 3 8 3 8

Приклад 8. Із протитанкової гармати по танку послідовно проводиться три

постріли. Ймовірність попадання в танк при першому пострілі дорівнює 0,4, мри

другому-0,6 і при третьому-0,8. Із попереднього досвіду відомо, що танк цілком

втрачає боєздатність при одному попаданні з ймовірністю 0,3, при двох і

ймовірністю 0,6 і при трьох - з ймовірністю 1. Визначити ймовірність Р(А) тої о,

що після трьох пострілів танк буде знищено.

Розв'язання. Позначимо події попадання в танк при першому, другому і

третьому пострілах через B

, B

відповідно, і розглянемо гіпотези:

- не відбудеться ні одного попадання,

Я, - відбулося одне попадання,

- "два",

- "три".

За теоремами додавання і множення ймовірностей несумісних подій знаходимо

ймовірності цих гіпотез

Р(Н

) = Р{В\ Вг В з) = 0,6

•

0,4

•

0,2 = 0,048,

Р(Н

) = Р(В

Вг) + Р{В\В

Вг) + Р(ВіВ

) =

= 0,4

•

0,4

•

0,2 + 0,6

•

0,6

•

0,2 + 0,6

•

0,4

•

0,8 = 0,296,

Р(Н

) = Р(В

Вг) + р(ВіВ

) + Р(ВіВ

) =

= 0,4

•

0,6

•

0,2 + 0,4

•

0,4

•

0,8 + 0,6

•

0,6

•

0,8 = 0,464,

Р(Н

) = Р(В

) = 0,4

•

0,6

•

0,8 = 0,192.

Умовні ймовірності події А при цих гіпотезах дорівнюють

Р(А/Н

) = 0, Р(А/Н

) = 0,3, Р(А/Н

) = 0,6, Р{АІН

) = 1.

Застосовуючи формулу (2.31), одержимо

Р(А) = Р(Н

)Р(А/Н

) + Р(Я,)Р(Л/ Я,) + Р(Н

)Р(А/ Я

) +

+Р(Н

)Р(А і Я

) = 0,296

•

0,3 + 0,464

•

0,6 + 0,192 = 0,56 .

2.2.4. Багаторазові випробовування. Формула Бернуллі

Проведення багатьох експериментів, наприклад, дослідження нових

вимірювальних інструментів або перевірка нових методик вимірювані.

Розділ II

робовування виконуються багаторазово при зберіганні певного комплексу

»в. У результаті кожного такого випробовування може з'явитись, а може і не

итись деяка подія А. Але при цьому дослідника цікавить не результат кожного

робовування, а загальна кількість появи події А при виконанні певної кількості

робувань п. Якщо ймовірність події

в кожному випробовуванні не залежить

результатів інших випробовувань, тоді такі випробовування називають

залежними відносно події А. Якщо незалежні випробовування

онуються в однакових умовах, тоді ймовірність події А у таких випробовуваннях

іа і та сама. Про сукупність п таких випробовувань говорять, що вони проведені

:хемою Бернуллі. Знайдемо основні закономірності, пов'язані з цією

мою. Для цього розв'яжемо таку загальну задачу:

проводиться серія п незалежних випробовувань, в кожному з яких може

ІИТИСЯ або не з'явитися деяка подія А (ймовірність її появи позначимо р).

;ба визначити ймовірність р (т) того, що при цьому подія А відбудеться т

ів в_п випробовуваннях, і не відбудеться (тобто з'явиться протилежна їй

ця А) п-т разів. _

Позначимо ймовірність протилежної події А через = 1 - p. При одному

іробовуванні може наступити або подія А, або подія А з ймовірностямир і q

повідно. Вони утворюють повну групу, а тому згідно теореми додавання

юнується така рівність:

p + q= 1. (2.32)

Для п = 2 можуть відбутися такі можливі випадки

АА, АА, АА, АА

мовірностями

, pq, qp, q

повідно. Але, якщо не враховувати той порядок, в якому з'являються події

то добутки А А , А А подій А і А будуть рівносильними (тотожними), тобто

і - А А. Тому можна вважати, що у двох випробовуваннях можуть відбутися

1 = 3 несумісних і єдино можливих події

АА,АА + А А, А А,

утворюють повну групу. Для них

? + 2pq + q

= (p + qY= 1. (2.33)

Так само для п - 3 можуть з'явитися такі окремі види результатів

пробовування з відповідними їм ймовірностями:

Елементи

теорії ймовірностей

AAA

2. AAA p

3. AAA p

AAA

5. AAA

РЧ

AAA pq

8. AAA

З p

З pq

(2.34)

Всі вони утворюють повну групу єдино можливих і несумісних випадків.

Отже, вважаючи події 2, 3, і 4, а також події 5, 6 і 7 рівносильними, можемо

записати

+ 3p

q + 3pq

= (p + q)

1 •

(2.35)

Порівнюючи події (2.34) і відповідні їм ймовірності, обчислені за формулою

(2.35), приходимо до висновку, що окремі члени лівої частини формули (2.35)

означають відповідно ймовірності того, що_у трьох випробовуваннях подія А

з'явиться 3, 2, 1,0 разів, а протилежна подія А - 0, 1, 2, 3 разів.

У загальному випадку для довільної кількості п випробовувань, проведених

за схемою Бернуллі, можуть з'явитися п + 1 окремо єдино можливих і несумісних

випадків з ймовірностями, які повинні задовольняти умову

(р + дУ= 1.

Розклавши вираз (2.36) за формулою бінома Ньютона, одержимо

(р + q)" =С''р"д

+C?-

p"-

q + C

+... +

С™

+...

... + c„W"

+c>r

+OV=i,

,0 0 л

(2.36)

(2.37)

де

С"=С.°= 1.

сг'=сі=я,

п-2

=Г

2 _ п(п - 1)

1-2 '

С" =•

т!

•

(п - т)!

кількість комбінацій, які можна утворити з п елементів по т .

(2.38)

Розділ II

гже, формулу (2.37) запишемо у вигляді

п п-1 п(п-1)

_2 2

р +

пр"

[

q + — - р q + ... +

+... + q" =1. (2.39)

1-2 '

m\(n-m)\

ірази (2.37) і (2.39) називають біноміальним розподілом

вірностей окремих можливих випадків з п випробовувань, проведених

емою Бернуллі. Кожний окремий доданок даного розподілу (2.37) є

ірністю того, що подія А з'явиться т разів в п випробовуваннях, тобто

(m) = C:p

. (2.40)

еієформула Бернуллі.

риклад 9. Для визначення деякої фізичної величини проведено 10

іювань. Рівноможливо, що в результатах цих вимірювань можуть з'явитися

ні похибки як додатні, так і від'ємні з ймовірностями р = q = ^ відповідно.

ібно визначити ймовірності того, що в наведеній серії вимірювань додатні

мні) похибки з'являться 0, 1,2, ..., 10 разів.

озв'язок задачі знаходимо за формулою (2.40)

(rn) = C™p

q"-

іри p = q р

(™) =

С™р"

рло) = с<:

РЛ і) = сі

Р.(2>-

РЛ 4) =

ґ J

v2,

1024

120

1024'

210

1024'

252

1024'

1024

1024'

РЛ 6) =

РЛ 7) =

РЛ 8) =

РЛ 9) =

^,(10)

210

1024'

120

1024'

"1024'

Сонтрольне співвідношення правильності проведених обчислень буде таким:

1р„(т) = 1.

яі=0

Елементи теорії ймовірностей

2.2.5. Найімовірніша кількість появи події при багаторазових випробовуваннях

За формулою Бернуллі (2.40) можна обчислити ймовірність довільної кількос гі

т появи події А при багаторазових випробовуваннях. Але для практичного

застосування біноміального розподілу ймовірностей досить часто буває важливим

знати, яка кількість появи цієї події буде найімовірнішою, тобто для якої кількості

т ймовірність Р

(т) матиме максимальне значення, вважаючи звичайно величини

р і п заданими.

Найімовірнішою кількістю появи події А в п незалежних

випробовуваннях можна вбажати таку кількість к

, для якої ймовірність (що

відповідає к

) буде більшою, або принаймні не меншою від ймовірності з кожної

іншої можливої кількості появи події А.

Позначимо ймовірність, яка відповідає найімовірнішій кількості

через Р

(к

{)

)

і запишемо її вираз через формулу Бернуллі

{K) = C

°P

q"-

°-

Згідно означення найімовірнішої кількості, ймовірності появи події А (к

()

+ 1)

разів або (k

- 1) разів принаймні не будуть перевищувати ймовірність Р

(к

), тобто

(к

)>Р

(к

+1),

(к

)>Р

(к

-1),

або за формулою Бернуллі

С*о

n-k

y-*

-i

0 п

«л

о > Г

«~

Р Ч /і Р ч

Отримані нерівності запишемо у розгорнутому вигляді

її p

«q"-

« >

^ А:

^ v

«a

° > - *b-i »-*6+i

які після спрощення будуть такими:

i>ZlzA Л

+1 д'

> —

п - к

+1 р

Розділ II

+ q>np-pk

, k

>np-q,

np - k

p + p > k

q , k

< np + p .

Зтже, остаточно отримаємо

np-q <k

<np +p. (2.41)

Якщо (np -q)- ціле число, тоді існують два значення найімовірнішої кількості

= np-q і к'

=np-q + \ = np + p,

:що (np -q)~ дробове число, то існує одне значення найімовірнішої кількості

,ине ціле число між дробовими числами праворуч і ліворуч в нерівності (2.41).

Якщо пр - ціле число, тоді існує одне значення найімовірнішої кількості

{)

= пр.

Приклад 9. Знайти найімовірнішу кількість попадань у мішень із 10 пострілів,

до ймовірність попадання при одному пострілі р = 0,6. _

Розв'язання. Якщо подія А - попасти в мішень, тоді р = р(А) = 0,6; р(А) = q-

- 0,6 = 0,4.

Скористаємося нерівністю

np-q <к

<пр + р.

Тоді 10

•

0,6 - 0,4 < к

< 10

•

0,6 + 0,6, або 5,6 <к

< 6,6 і остаточно к

= 6.

§ 2.3. Випадкові величини та їх ймовірнісні характеристики

Одне з важливих понять теорії ймовірностей - це випадкова величина,

падковою величиною називається величина, яка при одному випробовуванні

же прийняти те або інше своє можливе і наперед невідоме нам числове

ічення.

Надалі випадкові величини позначатимемо великими літерами латинської

гтки, наприклад X, Y, Z, ..., а їх можливі часткові значення - відповідними

лими літерами х , у., Zj, ... з належними індексами.

Розрізняють два типи випадкових величин: дискретні та неперервні.

Дискретною випадковою величиною називається величина, яка в результаті

пробовування може прийняти лише одне можливе своє значення зі скінченної

кількості, які можна перелічити.

Так, наприклад, дискретними випадковими величинами будуть:

1. Кількість попадань в ціль при п'яти пострілах.

2. Відносна частота потрапляння в мішень при 10 пострілах з гармати.

3. Кількість появи реверса при 10 підкиданнях монети і т.д.

Елементи теорії ймовірностей 77

У всіх цих прикладах випадкові величини можуть приймати такі відокрем ним

одне від одного певним проміжком можливі значення:

у прикладі 1: 0, 1, 2, 3, 4, 5;

у прикладі 2: 0, 0,1; 0,2; ...; 1,0;

у прикладі 3: 0, 1, 2, ..., 10.

Неперервною випадковою величиною називається величина, яка при

випробовуванні може'прийняти будь-яке одне можливе значення з нескінченнії

великої їх кількості, які неперервно заповнюють певний інтервал. Так, наприміал.

1) абсциса точки потрапляння в мішень при пострілі;

2) похибка вимірювання певного кута високоточним теодолітом;

3) віддаль точки потрапляння в мішень від центра мішені;

4) вага довільно взятої зернини пшениці і т.д.

У наведених прикладах окремі можливі значення випадкової величини

відокремлені одне від другого нескінченно малим проміжком

І ВСІ ВОНИ

неперервні

заповнюють певний інтервал. Кількість їх є нескінченно великою і обчиснп

и і\

числові значення не можна.

Між поняттями "випадкова подія" і "випадкова величина" існує тісний ш'и u

Справді, результат будь-якого випробовування, досліду, або експерименту можна

характеризувати як якісно, так і кількісно. Якісна характеристика речулмаїу

випробовування називається подією. Наприклад, слова "потрапляння в цілі." при

пострілі характеризують результат випробовування (стрільба в ціль) з якісного

юк

Через те "потрапляння в ціль", або "промах" є події. З іншого боку, речулі.іаі

випробовування можна характеризувати і кількісно. Будь-яка кількісна

характеристика результату випробовування, яка може прийняти одне ч ряду

можливих своїх числових значень, називається випадковою величиною. Отже, і

кожною випадковою величиною можна зв'язати певну випадкову подію, і панна мі

2.3.1. Закон розподілу випадкових величин

Для того, щоб охарактеризувати або описати випадкову величину X необхідно

задати всю сукупність можливих її значень і навести спосіб для визначення і\

ймовірностей. Отже, законом розподілу випадкової величини

називається співвідношення, яке встановлює зв'язок між окремими можливими

значеннями випадкової величини і відповідними їм ймовірностями.

Закон розподілу випадкової величини можна задавати в різній формі в

залежності від виду випадкової величини (дискретної чи неперервної). Так,

наприклад, для дискретної випадкової величини закон розподілу в найпростішій

формі можна задати у вигляді таблиці, в якій вказано всі її можливі значення і

відповідні цим значенням ймовірності (див. Табл. 2.1).

Розділ II

Таблиця 2.1.

Хі

Х\

Рі

Р2 Рг Рп

і таблиця називається рядом розподілу випадкової величини X.

jo буде відомою таблиця розподілу, то легко знайти, наприклад,

іість того, що дана випадкова величина потрапить на заданий інтервал,

•вірність того, що вона отримає значення, яке не перевищує певної межі, а

южна розв'язувати інші ймовірнісні задачі.

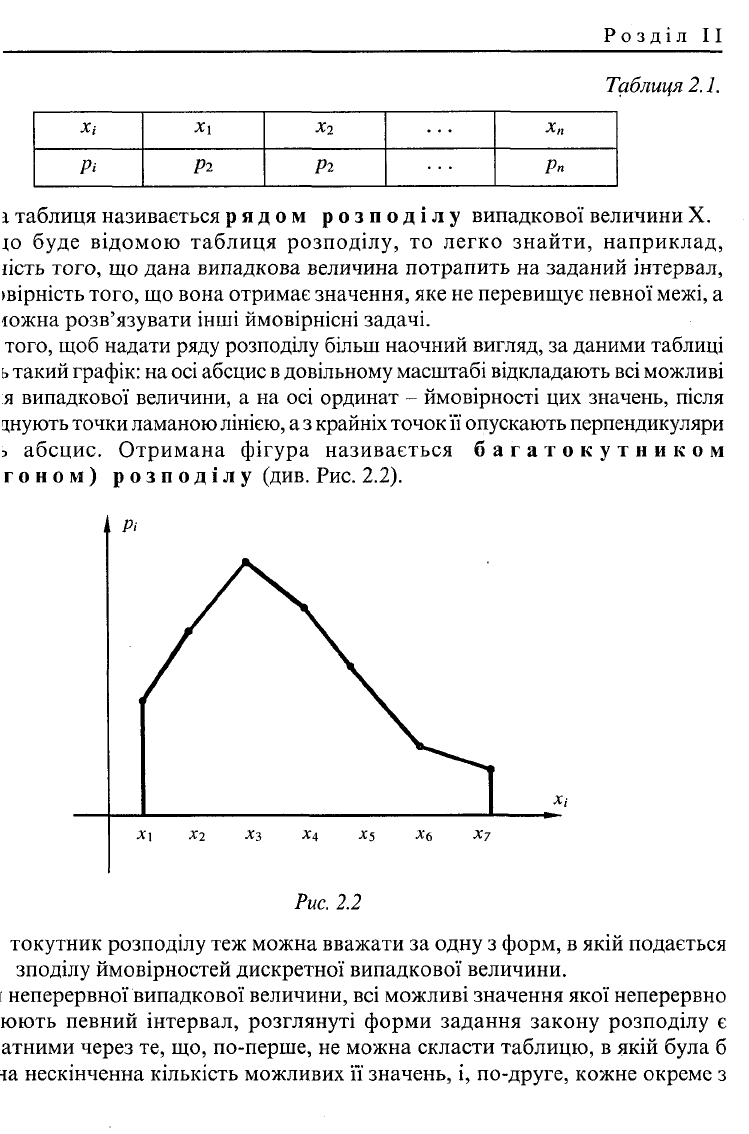
того, щоб надати ряду розподілу більш наочний вигляд, за даними таблиці

такий графік: на осі абсцис в довільному масштабі відкладають всі можливі

я випадкової величини, а на осі ординат - ймовірності цих значень, після

цнують точки ламаною лінією, а з крайніх точок її опускають перпендикуляри

з абсцис. Отримана фігура називається багатокутником

гоном) розподілу (див. Рис. 2.2).

атокутник розподілу теж можна вважати за одну з форм, в якій подається

юзподілу ймовірностей дискретної випадкової величини,

неперервної випадкової величини, всі можливі значення якої неперервно

юють певний інтервал, розглянуті форми задання закону розподілу є

атними через те, що, по-перше, не можна скласти таблицю, в якій була б

іа нескінченна кількість можливих її значень, і, по-друге, кожне окреме з

Елементи теорії ймовірностей

таких значень набуте з ймовірністю, яка дорівнює нулеві, що у подальшому буде

показано. Тому неперервна випадкова величина задається іншими формами

закону розподілу: функцією розподілу і функцією густини (щільності) розподілу.

Функцією розподілу випадкової величини X, яку прийнято

позначати F(x), називається ймовірність того, що випадкова величина X мри

випробовуванні набуде значення, меншого від х, тобто

F(x) = Р(Х < х), (2.42)

де х - біжуча змінна величина. Очевидно, що ця ймовірність є функцією аргумента .v.

Функцію розподілу іноді називають інтегральною функцією

розподілу, або інтегральним законом розподілу. Наведемо

її властивості.

1. Функція розподілу F{x) є функцією неспадною, тобто для х

>х, виконується

умова F(x

) > F(x

2. Для х —»функція розподілу прямує до нуля

Fi-oo)= lim F(x) = 0. (2.43)

3. Для X

—>

функція розподілу прямує до одиниці

F(+oo) = lim Fix) = 1. (2.44)

х—><»

Отже, значення функції розподілу Fix) як ймовірності деякої випадкової події

завжди знаходиться в межах від нуля до одиниці, тобто

0 < Fix) < 1. (2.45)

Функція розподілу Fix) є найбільш загальною формою задання закону

розподілу. Її можна використовувати для характеристики як дискретних, так і

неперервних випадкових величин.

Якщо дискретна випадкова величина X задана таблицею розподілу, то легко

визначити і функцію розподілу F(x) для кожного значення х. У цьому випадку вона

дорівнює сумі ймовірностей тих значень X, які лежать ліворуч від точки х, тобто

Fix) = P(X<x)= £Р(Х = х,.), (2.46)

Х(<Х

де нерівність х. < х під знаком суми означає, що сума береться для всіх значень х.,

менших від х .

Приклад 1. У незмінних умовах проводяться 5 незалежних випробовувань. У

результаті кожного з них може відбутися або не відбутися подія А. Ймовірність її

появи РІА) = 0,25. Випадкова величина Хе кількістю появи події А в даній серії

випробовувань. Визначити функцію розподілу Fix) і побудувати її графік.

Розділ II

чевидно, що випадкова величина ^набуває таких дискретних значень: 0,

5. Знаходимо ймовірності цих значень за формулою Бернуллі

P(X = k) = C

q"-

ількість всіх випробовувань у серії; к - кількість тих випробувань, в яких

ся подія Л; g =

-р = 0,75 - ймовірність протилежної події А . У результаті

мо таблицю (ряд) розподілу

Таблиця 2.2

Хк

1 2 3 4 5

Рк

0,237 0,395 0,264 0,088 0,015 0,001

начимо значення функції розподілу випадкової величини X.

ДЛЯ

х < 0

F(x)

= 0,

ДЛЯ

0 < х < 1

= 0,237,

ДЛЯ

1 < х < 2

F{x)

= 0,632,

ДЛЯ

2 < х < 3

F{x)

= 0,896,

для

3 < х < 4

Fix) = 0,984,

для

4 < х < 5

Fix)

= 0,999,

для

х > 5

Fix)

= 1.

іими числовими значеннями функції F(x) будуємо її графік (див. Рис.2.3).

рафіка видно, що функція розподілу дискретної випадкової величини є

розривною, східчастоподібною, яка змінюється стрибками кожен раз, коли

ова величина Сприймає одне з можливих своїх значень к. Величина стрибка

х дорівнює ймовірності Р(Х=к). Між двома сусідніми значеннями ^функція

талою. Очевидно, що сума всіх стрибків функції F(x) дорівнює одиниці.

Fix)

0,75

0,5

0 1 2 3 4 5

Рис.

2.3