Зазуляк П.М., Гавриш В.І. Євсєєва Е.М., Йосипчук М.Д. Основи математичного опрацювання геодезичних вимірювань
Подождите немного. Документ загружается.

Елементи теорії ймовірностей 81
Припустимо тепер, що кількість можливих значень випадкової величини X
необмежено зростає. Тоді необмежено зросте і кількість стрибків функції розподілу
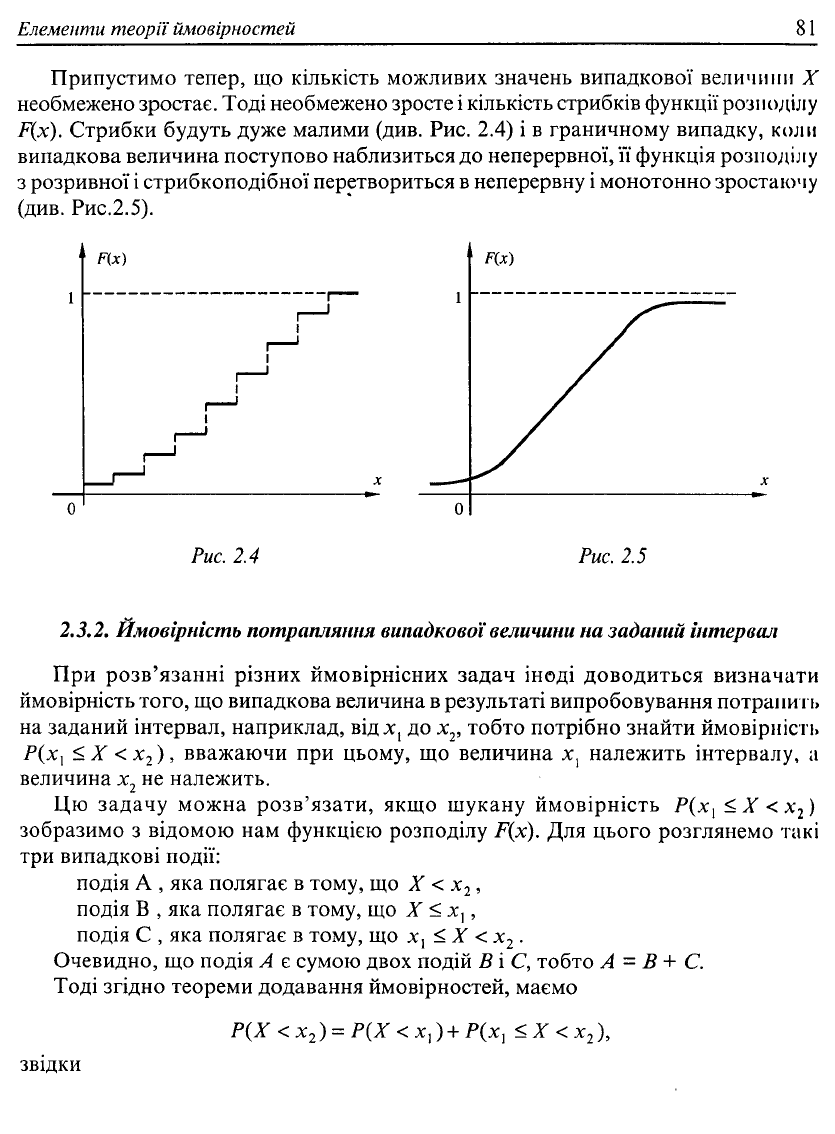
F(x). Стрибки будуть дуже малими (див. Рис. 2.4) і в граничному випадку, коли
випадкова величина поступово наблизиться до неперервної, її функція розподілу
з розривної і стрибкоподібної перетвориться в неперервну і монотонно зростаючу
(див. Рис.2.5).
Рис. 2.4 Рис. 2.5
2.3.2. Ймовірність потрапляння випадкової величини на заданий інтервал
При розв'язанні різних ймовірнісних задач іноді доводиться визначати
ймовірність того, що випадкова величина в результаті випробовування потрапить
на заданий інтервал, наприклад, від
лг,
до х
2
, тобто потрібно знайти ймовірність
Р(х
х
<Х <х
2
), вважаючи при цьому, що величина я, належить інтервалу, а
величина х
2
не належить.
Цю задачу можна розв'язати, якщо шукану ймовірність Р(х
х
<X<x
2
)
зобразимо з відомою нам функцією розподілу F(x). Для цього розглянемо такі
три випадкові події:
подія А , яка полягає в тому, що X < х
2
,
подія В , яка полягає в тому, що X <х
х
,
подія С , яка полягає в тому, що х, < X < х
2
.
Очевидно, що подія А є сумою двох подій В і С, тобто А = В + С.
Тоді згідно теореми додавання ймовірностей, маємо
Р(Х<х
2
) = Р(Х<х
1
) + Р(х
1
<Х<х
2
),
звідки

Розділ II
Р(х, <Х <х
2
) = Р(Х <х
2
)-Р(Х <х,),
Р(х, <Х <x
2
) = F(x
2
)-F(x
l
), (2.47)
і ймовірність того, що випадкова величина X потрапить на інтервал від х,
дорівнює приросту функції розподілу на цьому інтервалі,
риклад 2. За значеннями функції розподілу Р(х) у прикладі
1
(див. Табл. 2.2) знайти
рність потрапляння дискретної випадкової величини Хна інтервал (1,4).
тдно виразу (2.47) маємо
Р(1 < х < 4) = F(4) - F(l) = 0,984 - 0,632 = 0,352.
формулі (2.47) поступово зменшуватимемо довжину х
2
-х, інтервалу
2
), зміщуючи точку х
2
в напрямі до точки х
г
Тоді в граничному випадку,
точка х
2
співпадатиме з точкою х
р
ми замість ймовірності Р(х, < X <х
2
)
кимо ймовірність того, що випадкова величина Xприймає значення х,, тобто
Р(Х = х,) = lim Р(х
{
< X < х
2
) = lim {р(х
2
) - F(x
x
)}. (2.48)
зличина цього граничного значення ймовірності Р(Х = х,) залежить від того,
ЩКЦІЯ розподілу F(x) в ТОЧЦІ Xj є розривною, чи неперервною. Якщо в цій
вона є розривною, тоді граничне значення ймовірності, поданої виразом (2.48)
нює величині стрибка функції Дх). Якщо ж вона в точці є неперервною, то
Р(Х = х
]
)= lim Р(х, < X < х
2
) = F(x
2
)-F(x
x
) = 0 , (2.49)
>
ймовірність того, що неперервна випадкова величина X набуде довільного
юго значення
Xj
дорівнює нулеві.
2.3.3. Функція густини розподілу
t означення функції розподілу випливає, що для дискретної випадкової
чини вона є розривною, стрибкоподібною і неспадною функцією с^ого
центу х, значення якої обчислюються за формулою (2.46). Знайдемо тепер
іули, за якими можна обчислювати значення функції F(x) і визначати
іірності P(a < X < р) потрапляння на інтервал від а до (3 неперервної
дкової величини X. Для цього введено нове дуже важливе в теорії
ірностей поняття функції густини (щільності) розподілу,
озглянемо неперервну випадкову величину Хз функцією розподілу F(x), яку
vio вважати неперервною і диференційованою в кожній її точці. Візьмемо на
овій осі дві точки х і х + Ах. Ймовірність потрапляння величини Хна інтервал

Елементи теорії ймовірностей
83
(х + Ах) згідно формули (2.47) дорівнює приросту функції розподілу F(x) на цьому
інтервалі
Р(х < X < х + Ах) = F(x + Ах) - F(x). (2.50)
Відношення даного приросту до довжини Ах інтервалу (х, х + Ах) да» середнє
значення зміни ймовірності, що припадає на одиницю довжини в цьому інтервалі, тобто
Р(х<Х <х+Ах) =
Ах Ах
Зменшуватимемо довжину інтервалу і в граничному випадку для Ах
—»
0
одержимо похідну
ч
F(x + Ax)-F(x)
F'(x)= hm-Ь -J- ^ (2.51)
Ax
функції розподілу F(x), яку позначимо через f[x). Функція
f(x) = F'(x) (2.52)
називається функцією густини (щільності) розподілу або
диференціальним законом розподілу ймовірностей неперервної
випадкової величини X. Вона характеризує швидкість, з якою змінюється функція
розподілу F(x) в точці х.
Термін "густина розподілу ймовірностей" стає зрозумілим,
якщо скористатися механічною інтерпретацією поняття "розподіл
ймовірностей". Справді, можна уявити собі, що вся одинична маса
ймовірностей розподілена за певним законом на осі Ох в інтервалі всіх можливих
значень неперервної випадкової величини. Тоді, вважаючи за маси окремих точок
в цьому інтервалі величини, пропорційні ймовірностям, функціяДх) означатиме
ні що інше як лінійну густину (щільність) В ТОЧЦІ X.
Функція густини розподілу (2.52) є однією з форм задання закону розподілу
ймовірностей неперервних випадкових величин.
Тепер розглянемо неперервну випадкову величину X з функцією розподілу
F(x) і достатньо малий інтервал dx, прилеглий до точки х. Ймовірність того, що
величина X прийме одне зі значень в інтервалі (х, dx), дорівнює
Р(х <Х< х + dx) = F(x + dx) -F(x). (2.53)
Якщо функція розподілу F(x) є неперервною і має похідну F' в точці х, тоді
замість (2.53) можна записати
Р(х < X < х + dx) = F(x + dx) - F{x) = f{x)dx + є dx,
(2.54)
Розділ II
0, якщо dx
—>
0 . Вважаючи інтервал dx нескінченно малим, з формули
точністю до малих величин вищого порядку одержимо
P{x<X<x + dx)-J{x)dx. (2.55)
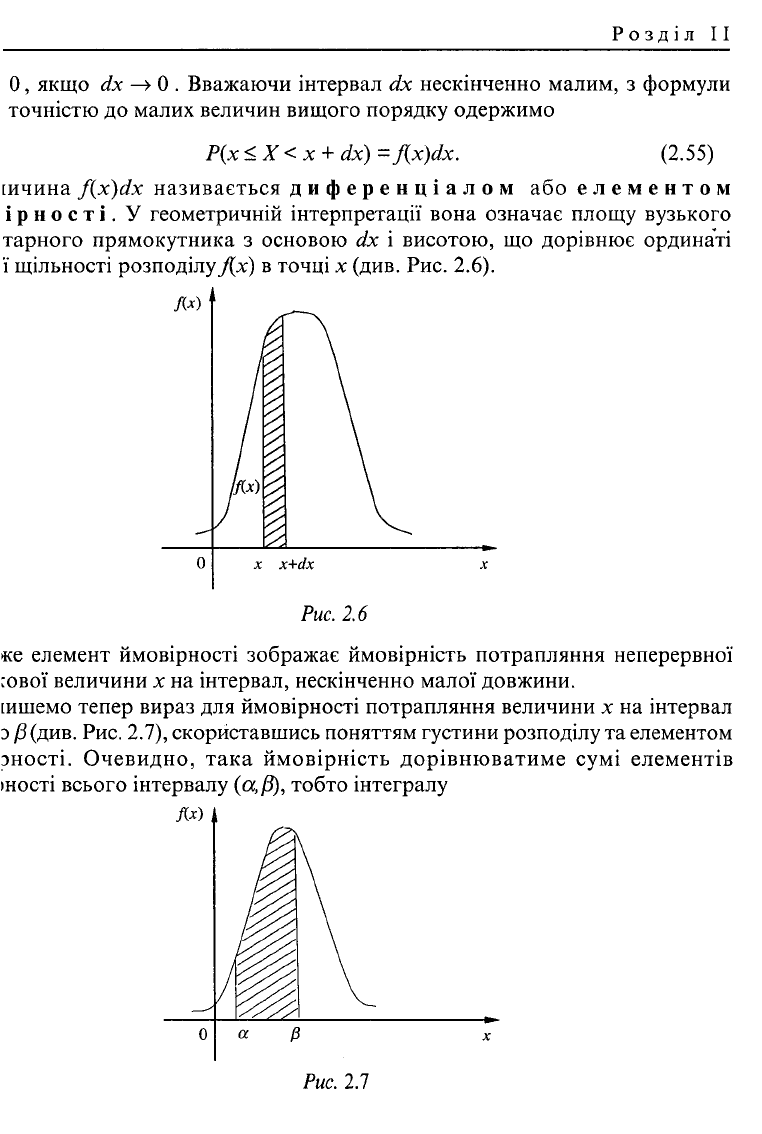
іичина f(x)dx називається диференціалом або елементом
і р н о с т і. У геометричній інтерпретації вона означає площу вузького
тарного прямокутника з основою dx і висотою, що дорівнює ординаті
ї щільності розподілу Дх) в точці х (див. Рис. 2.6).
«е елемент ймовірності зображає ймовірність потрапляння неперервної
сової величини х на інтервал, нескінченно малої довжини,
іишемо тепер вираз для ймовірності потрапляння величини х на інтервал
з
/3
(див. Рис. 2.7), скориставшись поняттям густини розподілу та елементом
зності. Очевидно, така ймовірність дорівнюватиме сумі елементів
іності всього інтервалу
(сс,Р),
тобто інтегралу
Елементи теорії ймовірностей
85
а
Р(сс<Х<р) = \f(x)dx. (2.56)
а
Геометрично ця ймовірність зображається площею, обмеженою віссю ()\,
кривою функції густини розподілу Дх) та двома ординатами j(a) i/f/3).
Скориставшись виразами (2.52) та (2.56), можемо записати вираз для функції
неперервної випадкової величини X. За означенням
F(x) = P(X<x),
або
F(x) = Р(-оо < X < х),
тобто
F(x)= j f(x)dx. (2.57)
—оо
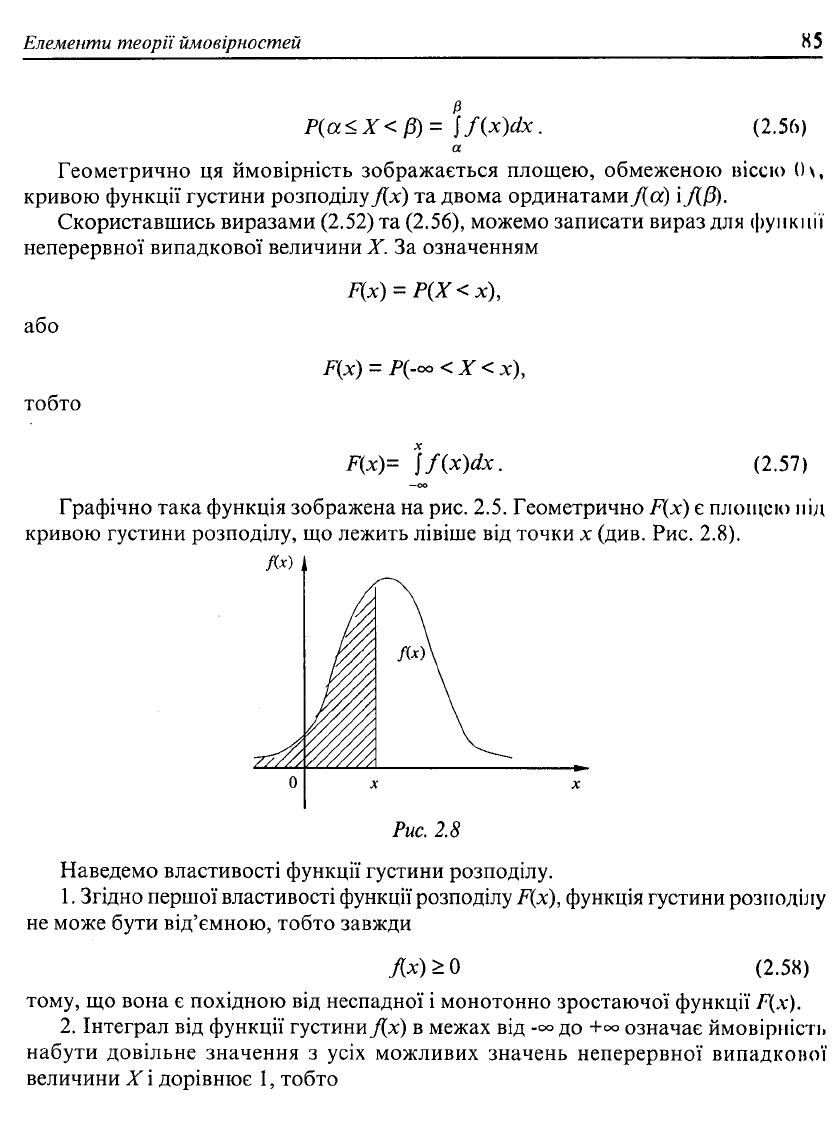
Графічно така функція зображена на рис. 2.5. Геометрично F(x) є площею під
кривою густини розподілу, що лежить лівіше від точки х (див. Рис. 2.8).
Наведемо властивості функції густини розподілу.
1. Згідно першої властивості функції розподілу F(x), функція густини розподілу
не може бути від'ємною, тобто завжди
Лх)>0 (2.58)
тому, що вона є похідною від неспадної і монотонно зростаючої функції F(x).
2. Інтеграл від функції густини Дх) в межах від
-оо
до +оо означає ймовірність
набути довільне значення з усіх можливих значень неперервної випадкової
величини X і дорівнює 1, тобто

Розділ II
F(+oo) = Р(-оо < X < +°°) = j f{x)dx =
1
(2.59)
подія -оо < X < +оо є достовірною. Геометрично це означає, що повна
, кривою густини розподілу дорівнює одиниці.
шість густини розподілу як видно з формули (2.51) є оберненою до
сті випадкової величини. Функція розподілу є безрозмірною як
ть події.
інемо приклади.
іад 3. Функція розподілу неперервної випадкової величини X задається
и:
зефіцієнт а;
іункцію густини розподілу;
мовірність потрапляння величини Хна інтервал від 0,25 до 0,5.
зання.
Іля знаходження коефіцієнта а скористаємося властивістю функції
озподілу, поданої виразом (2.57), та формулою (2.52). У нашому випадку
х) = 2ах і
0, якщо х < 0,
F(x) =
-
ах
2
,якщо 0<х<1,
1, якщо х>1.
.2
J / {x)dx = 2а j xdx = 2а
ґ
= а-1-0 = а = 1;
о о
2
о
)ункція густини розподілу тепер матиме вигляд
0,
якщо х<0,
/(х) =
-
2х,якщо 0<х<1,
1,якщо х>1.
la формулою (2.47) маємо
Р(0,25 < х < 0,5) = ДО,5) - ДО,25) = 0,5
2
- 0,25
2
= 0,1875.
лад 4. Функція густини розподілу задана виразом
7Г(1
+ Х
2
)
( оо <
X
< +оо)

Елементи теорії ймовірностей 87
а) Потрібно знайти вира для з функції розподілу;
б) обчислити ймовірність потрапляння випадкової величини X на інтервал (0; 5).
Розв 'язання.
а) Із використанням виразу (2.57) маємо
F(x) = J І——dx =
—
arctgxV =
—
\arctgx - artg{-°°)\ =
—
+
—
arctgx,
-~7Г(
1
+
X
) n °° Tt 2 7t
тобто функція розподілу має вигляд
F(x) =
0,ЯКЩО Х<-°°,
1 1
—
+ — arctgx,ЯКЩО -°°<Х<+°°,
2 л
1,ЯКЩО х>+°°.
б) Р(0<х<5)= f—
d
^— = -arctgx\l =
—
(arctg5 - 0) = 0,435
•
q 7l(l + X ) n
0
71
2.3.4. Числові характеристики випадкових величин
Функція розподілу випадкової величини X, яка пов'язана з рядом розподілу
(якщо величина дискретна) і з функцією густини розподілу (якщо величина
неперервна), є повною ймовірнісною характеристикою.
У більшості випадків функція розподілу, або функція густини розподілу,
встановлюється, виходячи з тих чи інших властивостей випадкової величини,
теоретичним шляхом у вигляді математичної формули, в яку входять змінна
випадкова величина X як аргумент і один або декілька параметрів, кожен з яких
характеризує ту чи іншу основну властивість випадкової величини.
Однак, при розв'язуванні багатьох практичних задач з випадковими величинами,
не завжди є необхідність користуватися законом розподілу в повній його формі. Для
цього іноді досить знати лише числові значення деяких параметрів, які кількісно
характеризують найбільш істотні властивості закону розподілу. Такими параметрами
можуть бути, наприклад, деяке середнє значення випадкової величини, біля якого
групуються інші можливі її значення, або величина, яка характеризує міру їх
розсіювання. Такі числові значення параметрів закону розподілу називаються
числовими характеристиками. Деякі з них можуть і не входити в явному вигляді в
математичний вираз закону розподілу даної випадкової величини. У таких випадках
значення їх визначають як функції інших основних параметрів.
Розглянемо найбільш важливі і найчастіше вживані на практиці числові
характеристики законів розподілу випадкових величин.

Розділ II
еред числових характеристик випадкових величин є група, яка характеризує
ження випадкової величини на числовій осі, тобто такі характеристики
/ють деяке середнє, орієнтовне значення, біля якого групуються всі можливі
гння випадкової величини, або значення, яке з'являється з найбільшою
іірністю. До цієї групи відносяться математичне сподівання,
а, медіана.
[айбільш важливою характеристикою з цієї групи є математичне
д і в а н н я . Це центр групування або центр розподілу окремих значень
дкової величини (його часто називають середнім значенням) і його
ачають М[Х\, т
х
.
озглянемо дискретну випадкову величину, яка може приймати можливі
ення АГ,, х
2
, ..., х
п
з ймовірностями p
t
, р
2
, ..., р
п
. Припустимо, що цих
іірностей ми не знаємо.
[ля їх визначення проведемо N незалежних між собою спостережень, в
тьтаті яких випадкова величина прийме одне з можливих своїх значень,
тустимо далі, що значення
х, з'явилося т
і
разів,
х
2
з'явилося т
2
разів,
X " " т " ",
П П '
п
іому Yj
m
i =N. Знайдемо тепер середнє арифметичне із результатів
І
тережень
_ х,т, +
х-,т-,
+
• • •
+ х„т„ т, т-, т„
x=-
J
—
!
—
J
—
!L
= х, — + х
2
— +
• • •
+ х„ —, (2.60)
N
]
N
2
N " N ' '
о, середнє арифметичне дорівнює сумі добутків кожного можливого значення
.дкової величини на відповідну йому відносну частоту.
те, згідно формули (2.3)
І™ ^7 =
А-
0' = 1,л),
чу рівність (2.60) можна записати так:
п
lim х = Лх^, .
)тже, математичне сподівання є сподіваним середнім і подається виразом
m
x
=M[x}=f
J
x
i
p
i
. (2.61)
/=і

Елементи теорії ймовірностей 89
Формула (2.61) відповідає випадку дискретної випадкової величини Дим
обчислення математичного сподівання неперервної випадкової не вичини
п
необхідно в формулі (2.61) скінчену суму Y,
x
iPi замінити означеним ппеїрімом,
і
а під знаком інтеграла замість ймовірностей р. (і = 1,п) записані елемені
ймовірності/(х)<&:, тобто
м[х] = °]xf(x)dx. (2.(у?)
Крім математичного сподівання для визначення на числовій осі типового значення
випадкової величини застосовують ще моду MjX\ та медіану М[Х\ (або М
о
, А/ ).
Модою називається таке значення випадкової величини X - х
ц
, при якому
ймовірність Р(Х = х
0
) має максимальне значення. Для дискретної випадкової
величини це значення відповідає найвищій вершині багатокутника розподілу (див.
Рис.2.2), а для неперервної - абсциса, яка відповідає найвищій точці кривої гус
І
ПЕНІ
розподілу (див. Рис. 2.6).
Медіаною дискретної випадкової величини Хназиваєтьсятакеїї значення,
при якому
Р(Х<М
е
) = Р(Х>М) = (2.63)
тобто ймовірність того, що величинах прийме значення, менше від М
е
дорівнює
ймовірності того, що вона прийме значення, більше від М. Отже, для медіани
1
значення функції розподілу буде F(M
е
) = —.
Для неперервної випадкової величини медіана визначається співвідношенням
М
е
оо 1
lf(x)dx= jf(x)dx = ~. (2.64)
-о» м
е
2
У геометричній інтерпретації це означає, що медіана є абсцисою такої точки
числової осі, ордината якоїДМ) ділить площу, обмежену кривою функції
щільності розподілу і віссю Ох, порівну (див. Рис.2.9 5
і
, = S
2
).
У загальному випадку при несиметричному законі розподілу ймовірності
числові значення характеристик М{Х\, М
о
і М
е
е різними, а при симетричному
законі - вони є величинами, такими, що дорівнюють між собою.
Всі числові характеристики випадкової величини описують ту чи іншу
властивість розподілу (або кажуть - певний момент розподілу).Тому їх
характеристики називають ще моментами.

Розділ II
Поняття моменту широко використовується в механіці для опису розподілу
: (статичні моменти, моменти інерції тощо). Для опису основних властивостей
зподілу випадкових величин поняття момента в теорію ймовірностей
іровадив російський математик Чебишев П.І. Найчастіше використовують
іаткові та центральні моменти. Позначатимемо їх через v і
/л
відповідно.
Початковим моментом s-ro порядку v
s
[z] для дискретної
іадкової величини X називається сума
=£*?/>/, (2.65)
ля неперервної випадкової величини інтеграл
v
s
\x]='\x
s
f(x)dx. (2.66)
Порівнюючи формули (2.65), (2.61) і (2.66), (2.62) легко помітити, що
тематичне сподівання М[Х\ є початковим моментом першого порядку
іадкової величини X (s = 1). Отже, на підставі цього можна дати загальне
іачення, а саме, початковим моментом випадкової величини s-то порядку
іивається математичне сподівання 5-го степеня цієї величини
V
S
[X] = M[X
S
}. (2.67)
Введемо тепер поняття "центрованої випадкової величини". Центрованою
падковою величиною випадковоївеличини^називаєтьсявідхилення
о
ід математичного сподівання т
х
. Позначимо її через X, тобто
Х = Х-т
х
. (2.68)
