Зазуляк П.М., Гавриш В.І. Євсєєва Е.М., Йосипчук М.Д. Основи математичного опрацювання геодезичних вимірювань

Подождите немного. Документ загружается.

Елементи теорії ймовірностей

101

Кількість т появи події А є дискретною випадковою величиною. У геодезичній прлк

ІЩІ

такою величиною може бути кількість додатніх та від'ємних похибок вимірювані.

Отже, біноміальний закон як закон дискретної випадкової величини може бу

заданий рядом, або таблицею розподілу (див. Табл.2.1), де ймовірність кожної о

значення випадкової величини обчислюється за формулою Бернуллі.

Таблиця 2.1

Xj =

0 1 ... m

... n

Рп,,.»

c>Y

c>V

За таким рядом можна побудувати багатокутник розподілу (подати закон

розподілу графічно).

Функція біноміального розподілу буде мати такий вигляд:

0> якщо т< 0,

S Р

> якщо 0<т<п, (2.W)

F(m) =

якщо т>п.

Основні числові характеристики біноміального розподілу можна отримані,

скориставшись виразами початкових моментів перших чотирьох порядків.

За формулою

отримаємо вирази

=M[x

] = Zxf

і= 1

v, =Af[x]= Y,mC"

q"'

т=0 '

=М[х

]= Zrn

C™p

q"-

т=0

= М[х

] = J

C™p'

т=0

= А/[х

] = Zrn

C™p

q"-

т=0

(2.100)

(2.101)

(2.102)

(2.103)

Розділ II

У виразах (2.100)-(2.103) згідно співвідношення (2.37)

їс:

д"-

=(р + яГ. (2.104)

т=0

Продиференціюємо рівність (2.104) за змінноюр послідовно 1,2,3,4 рази, після

о отримаємо

ІтС

у-у-"'=«(^

)

, (2.105)

т=0

-Y)C™р"'~

q"~

= п(п - 1)(р + q)"'

, (2.Ю6)

m=0

£rn(m-l)(m-2)C™p

}

q"-

=n(n-l)(n-2)(p + q)"-

}

, (2.107)

ni-0

im(m-l)(m-2)(m-3)C™ p

q"~

= n{n - l)(n - 2)(« - 3)(/> + q)

. (2.108)

m=0

А тепер помножимо ліву і праву частини рівності (2.105) на р

imC:

q"-

y-\

m=0

кої одержимо згідно виразу (2.100)

V, = рп(р + q)

, а оскількир + q = 1, то

v, =ир,або М[Х] = пр. (2.109)

Отже, вираз (2.109) дає можливість обчислити математичне сподівання

ькості появи випадкової події, наприклад, додатньої похибки вимірюванння

незалежних випробовуваннях.

Модою M

біноміального розподілу буде найімовірніша кількість появи

іадкової події, яка визначається нерівністю (2.41)

np-q <к

<пр +

, або

+р-І <к

<п

Очевидно, що відстань між М

і М[Х\ не перевищує одиниці.

Далі помножимо ліву і праву частини рівності (2.106) на

tm(m -1 )C™

q"-"' = п

(п - \){

+ q)"'

m=0

Елементи теорії ймовірностей

103

та, розкривши дужки із використанням виразів (2.100) і (2.101), отримаємо

-v, = п

-пр

або, враховуючи, що v

=np останню рівність перепишемо

=пр + п

- пр

А тепер скористаємось виразами для дисперсії

D[X] = v

-vf

та початкових моментів v

і v, у результаті чого матимемо

D[X] = пр + п

-пр

-п

або остаточно дисперсія біноміального розподілу буде

D[X] = np(l-p) = npq, (2.110)

звідки можна знайти і середнє квадратичне відхилення

=Jnpq. (2.111)

Якщо помножити вирази (2.107) і (2.108) відповідно нар

і/>

, та скориста

мої

виразами (2.75), (2.76) для ц

і ц

, то отримаємо співвідношення для коефіціпі іа

асиметрії та ексцесу біноміального розподілу

=(q~p)/Jwq, (2.И2)

=(\-6pq)/npq. (2.113)

За даними прикладу 9 (§ 2.2) побудуємо ряд та багатокутник розподілу,

знайдемо значення функції розподілу та побудуємо її графік, обчислимо числоиі

характеристики та ймовірність потрапляння на інтервал (3;7).

1. Будуємо ряд розподілу, використовуючи для цього обчислення, проведені

на стор. 46.

Таблиця 2.2

Ші

0 1 2

5 6 7 8

Рі

1024

120

1024

210

1024

252

1024

210

1024

120

1024

2. Багатокутник буде мати вигляд

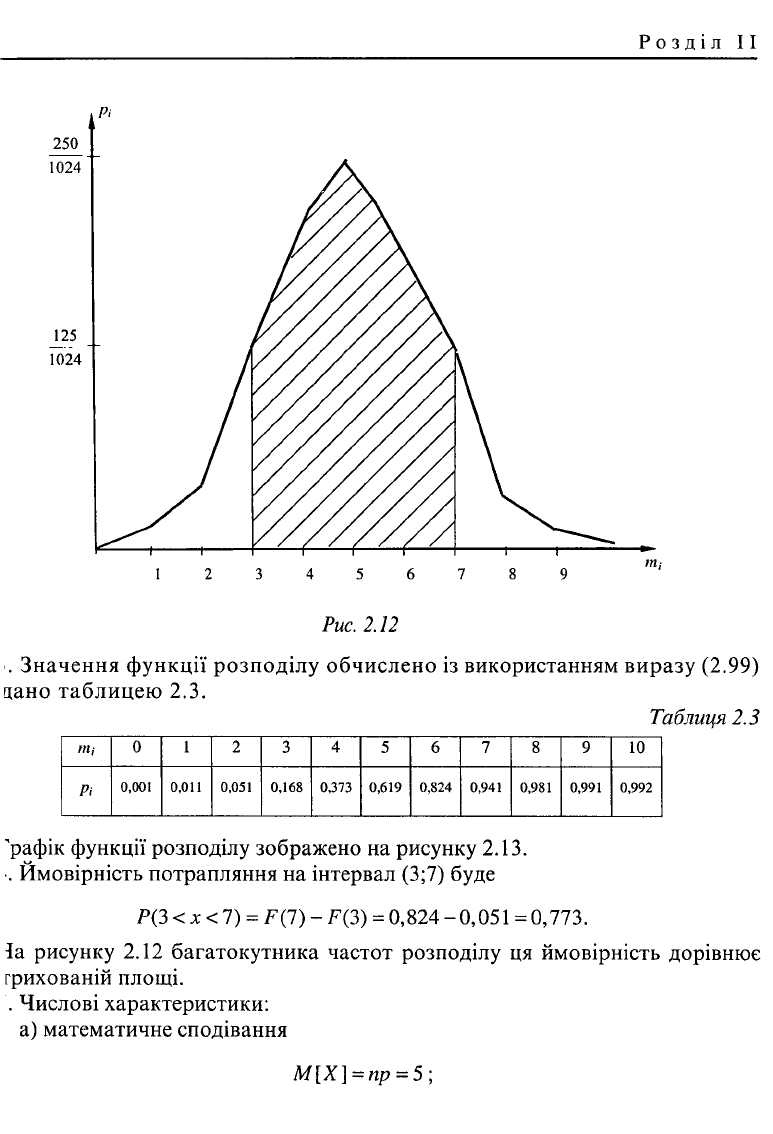
Розділ II

Рис.

2.12

. Значення функції розподілу обчислено із використанням виразу (2.99)

цано таблицею 2.3.

Таблиця 2.3

Т,

0 1 2

5 6 7 8 9

РІ

0,001 0,011 0,051

0,168 0,373 0,619 0,824

0,941

0,981 0,991 0,992

Графік функції розподілу зображено на рисунку 2.13.

•. Ймовірність потрапляння на інтервал (3;7) буде

Р(3 < * < 7) = F( 1) - F(3) = 0,824 - 0,051 = 0,773.

la рисунку 2.12 багатокутника частот розподілу ця ймовірність дорівнює

грихованій площі.

. Числові характеристики:

а) математичне сподівання

М[Х] = пр = 5;

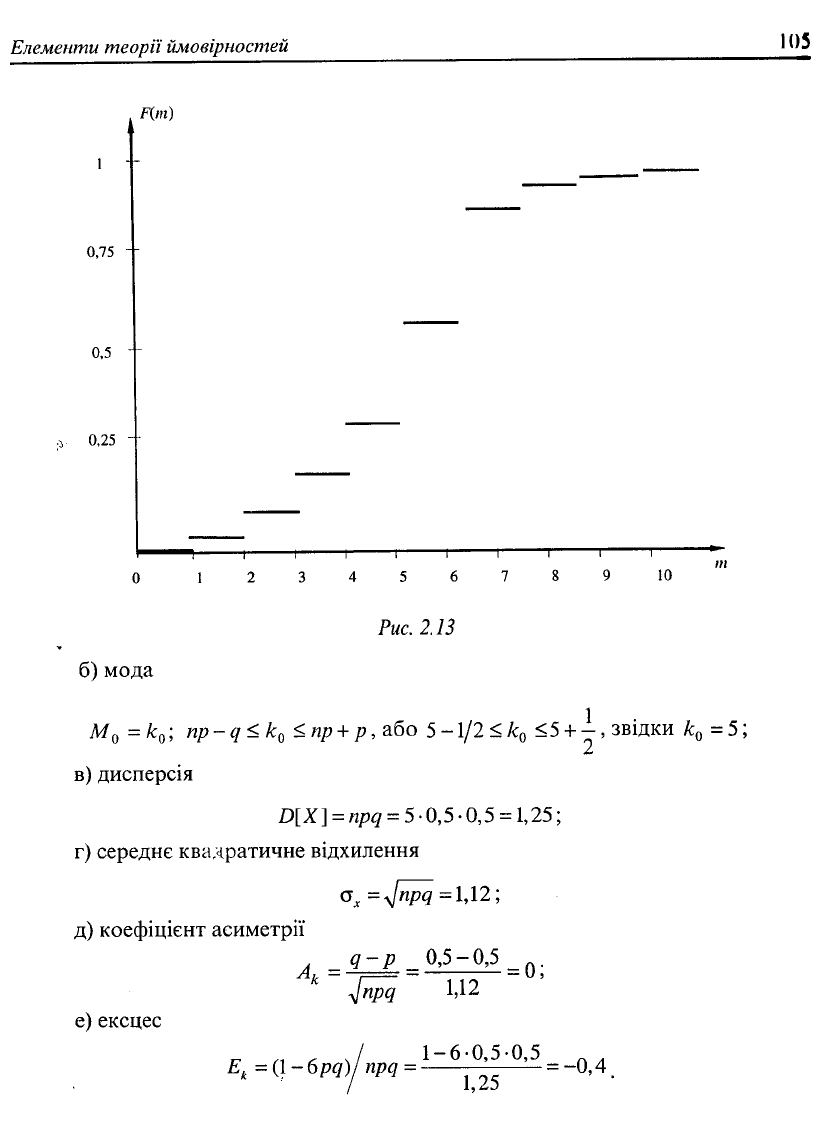
Елементи теорії ймовірностей

105

F(m)

0,75

0,5

0,25

б) мода

1 1 1 1 1 1 Г—

1 2 3 4 5 6 7

Рис. 2.13

-І 1—

9 10

= к

; пр - q < к

< пр + р, або 5 -1/2 < к

<5 + -, звідки к

= 5;

в) дисперсія

D[X] = npq = 5-0,5-0,5 = 1,25;

г) середнє квадратичне відхилення

=^fnpq= 1,12;

д) коефіцієнт асиметрії

д-р 0,5-0,5

А =

•Jnpq ІД

= о;

е) ексцес

IT п * J 1-6-0,5-0,5

= (1-6pq) npq = — = -0,4.

Розділ II

2.4.2. Рівномірний розподіл

деяких практичних задачах доводиться мати справу з такими неперервними

[ковими величинами, про які наперед відомо, що, по-перше, їх можливі

ння знаходяться на певному інтервалі, і, по-друге, на цьому інтервалі всі ці

ння мають однакову можливість своєї появи. Про такі величини говорять,

>ни розподіляються за законом рівномірної густини.

іприклад, результатом деяких обчислень виявилось число 4,38, про яке

о, що воно отримано шляхом заокруглення великої кількості знаків. Із

ша заокруглення очевидно, що можливі похибки цього наближеного числа

дяться в межах від -0,005 до +0,005. Крім цього, всі похибки появляються з

овою ймовірністю тому, що, немає підстав вважати, що одна з них з'явиться

шою ймовірністю, а друга - з меншою.

гже, похибки заокруглення взагалі є величинами випадковими зі сталою

пою розподілу ймовірностей. Такі ж властивості мають і похибки відліків

іними шкалами геодезичних інструментів, коли виконується заокруглення

у до найближчого цілого значення.

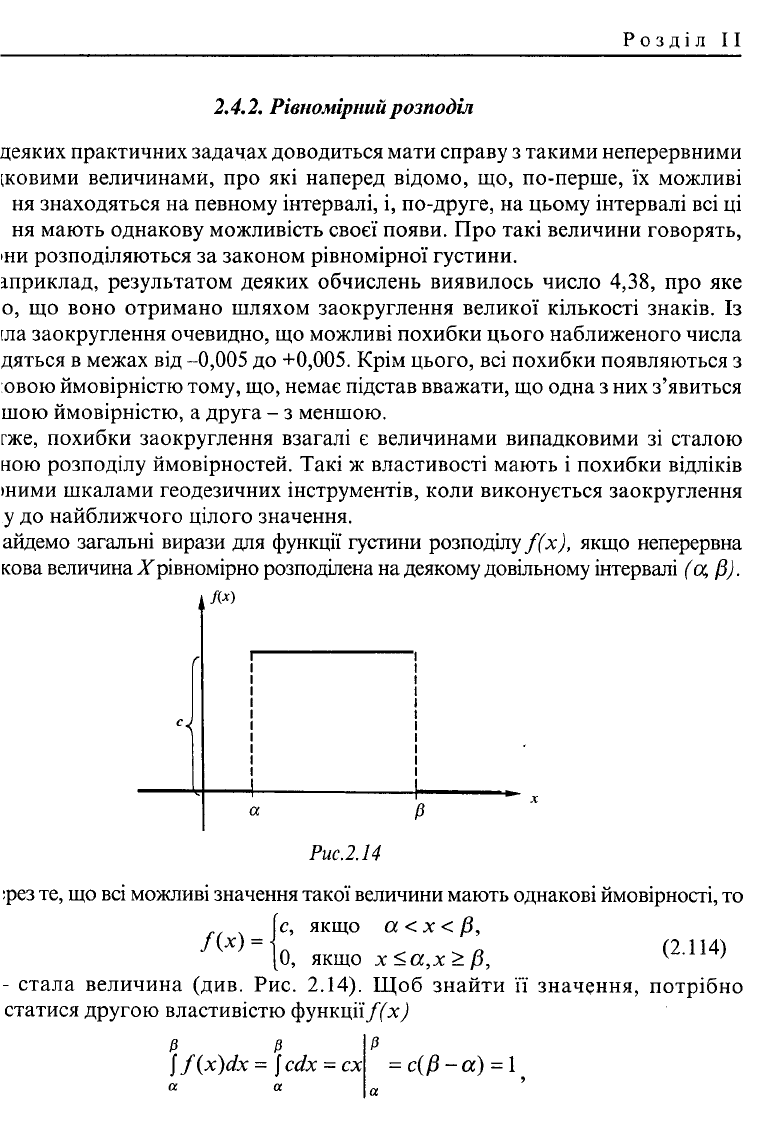
айдемо загальні вирази для функції густини розподілу f(x), якщо неперервна

кова величина X рівномірно розподілена на деякому довільному інтервалі (а, (3).

Рис.2.14

:рез те, що всі можливі значення такої величини мають однакові ймовірності, то

[с, якщо а< х < /З,

/W =

{o, якщо х<а,х>/3, (2-114)

- стала величина (див. Рис. 2.14). Щоб знайти її значення, потрібно

статися другою властивістю функції/(х)

f / (x)dx = J cdx = cx

= c(fi-a) = l

Елементи теорії ймовірностей

107

ЗВІДКИ

с =

Р-ос'

Отже, вираз для функції густини розподілу матиме такий вигляд:

„ , якщо а <х < В,

р-а

q якщо х < сс,х > р.

(2.115)

(2.116)

Функцію розподілу F(x) знаходимо за формулою (2.57) замінивши нижню

межу інтегрування лівою межею інтервалу (а,Р), на якому існує рівномірний

розподіл

F(x) =

\dx =

•х\„ =•

х-а

Р-сс'а Р-а

|а

Р-а'

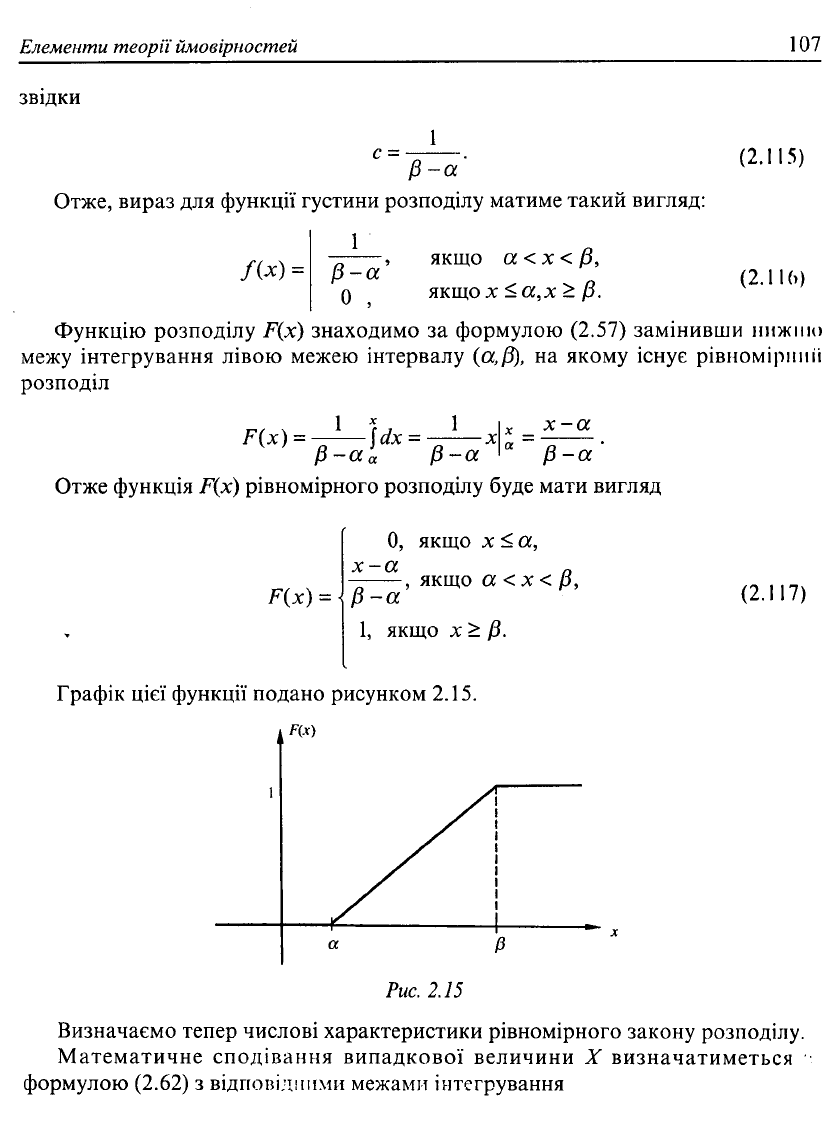
Отже функція F(x) рівномірного розподілу буде мати вигляд

F{x) =

0, якщо х < а,

х-а

-, якщо а < х < р,

р-а

1, якщо X > р.

Графік цієї функції подано рисунком 2.15.

F(x)

(2.117)

Рис. 2.15

Визначаємо тепер числові характеристики рівномірного закону розподілу.

Математичне сподівання випадкової величини X визначатиметься

формулою (2.62) з відповідними межами інтегрування

Розділ II

і/3-а 2ф-а) 1° 2(/3-а)'

(2Л18)

іівномірного закону розподілу випадкової величини

ЛТ

моди не існує,

о означення медіани матимемо

Р(Х < Me) = Р(Х >Ме) = ^,

Ме =

сс

+ Р

(2.119)

ерсія рівномірно розподіленої випадкової величини із використанням

(2.79) дорівнюватиме

D[X] =

P-al

а + Р

dx =

(Р-аУ

(2.120)

и знаходимо середнє квадратичне відхилення величини X

(2.121)

іідок симетричності закону розподілу коефіцієнт асиметрії дорівнюватиме

шзначення ексцесу знаходимо центральний момент четвертого порядку,

ївшись формулою (2.72)

Р-ССа

сс

+ Р

dx =

(Р-сс)

(2.122)

а.

80(j8-а)

(2.123)

Елементи теорії ймовірностей

109

Ймовірність потрапляння рівномірно розподіленої випадкової величини Хна

інтервалі (a, b) знаходимо, інтегруючи формулу густини в межах від а до Ь, тобто

b-a

P(a <Х <b) = -^——\dx

•

(2.124)

FI-OCA P~A

Розглянемо приклади.

Приклад 1. Випадкова величина X підпорядковується закону рівномірної

густини на інтервалі [0;2]. Написати вирази для густини розподілу ймовірностей та

функції розподілу випадкової величини X. Знайти ймовірність потрапляння на

інтервал

°'2

Розв

'язання.

Користуючись виразом (2.116) для функції густини рівномірного

розподілу матимемо

0, для х < 0,

—, для 0<х<2,

0, для х>2.

Функція розподілу згідно співвідношення (2.117) буде мати вигляд

F(x) =

Ймовірність потрапляння на інтервал

0, для х < 0,

х/2, для 0<х<2,

1, для х>2.

V У

знаходимо так:

0<Х<-

— I

dx =

—

= 0,25.

Приклад 2. Випадкова величина Хмає рівномірний розподіл з математичним

сподіванням т

= 1 та дисперсією D

= 3. Знайти вираз для функції густини

ймовірностей розподілу.

Розв'язання. Математичне сподівання і дисперсія рівномірно розподіленої

випадкової величини відповідно дорівнюють

т, =

а +

£> =

ЛЬ-af

Розділ II

') інтервал розподілу.

айдемо межі інтервалу а і

Ь.

Для цього скористаємося наведеними виразами

ишемо рівності

а +

= 1,

(b-af _

2 12

зв'язавши їх відносно а і Ь, отримаємо а = -2, b - 4.

епер знайдемо функцію густини розподілу, використавши співвідношення (2.116)

0, якщо х < -2,

1/6, якщо -2 < х < 4,

0, якщо х > 4.

2.4.3. Нормальний закон розподілу. Параметри нормального закону

ірмальний закон розподілу або закон Ґаусса в теорії ймовірностей відіграє

/ роль і серед усіх інших можливих законів розподілу займає особливе місце,

юнюється тим, що, по-перше, нормальний закон є найбільш розповсюдженим

юді законом розподілу ймовірностей випадкових величин і, по-друге, він є

чним законом, до якого наближаються деякі інші закони, наприклад,

іальний, а також, з багатьма законами розподілів випадкових величин він

даться в тісному зв'язку.

)рмальний закон виникає майже завжди тоді, коли окремі можливі

ІНЯ випадкової величини можна розглядати як сумарний ефект впливу

ьох відомих і невідомих нам випадкових і другорядних (не основних)

ін, кожна з яких незалежно від інших спричиняє появу в результаті одного

зреження даної випадкової величини дуже малої елементарної похибки. У

>ному ефекті вони обумовлюють коливання результатів багатьох

ережень випадкової величини біля деякого середнього її значення

натичного сподівання). До таких величин, наприклад, належать похибки

с вимірювань, які доводиться виконувати в геодезії, астрономії та інших

їх науки, лінійні розміри деталей одного типу при масовому їх виробництві,

іі точок попадання в мішень від центра мішені, які з'являються після

оразових повторних пострілів по мішені при незмінних умовах. Усі ці

кові величини і багато інших, подібних їм, з більшою або меншою мірою

ження підпорядковуються нормальному закону.

)рмальний закон розподілу ймовірностей неперервної випадкової величини X

іьному вигляді визначається такою функцією густини розподілу: