Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика. Решебник

Подождите немного. Документ загружается.

120

Гл.

5. Графики функций

lim —

а:->2+0 4(2 - хУ

4-00.

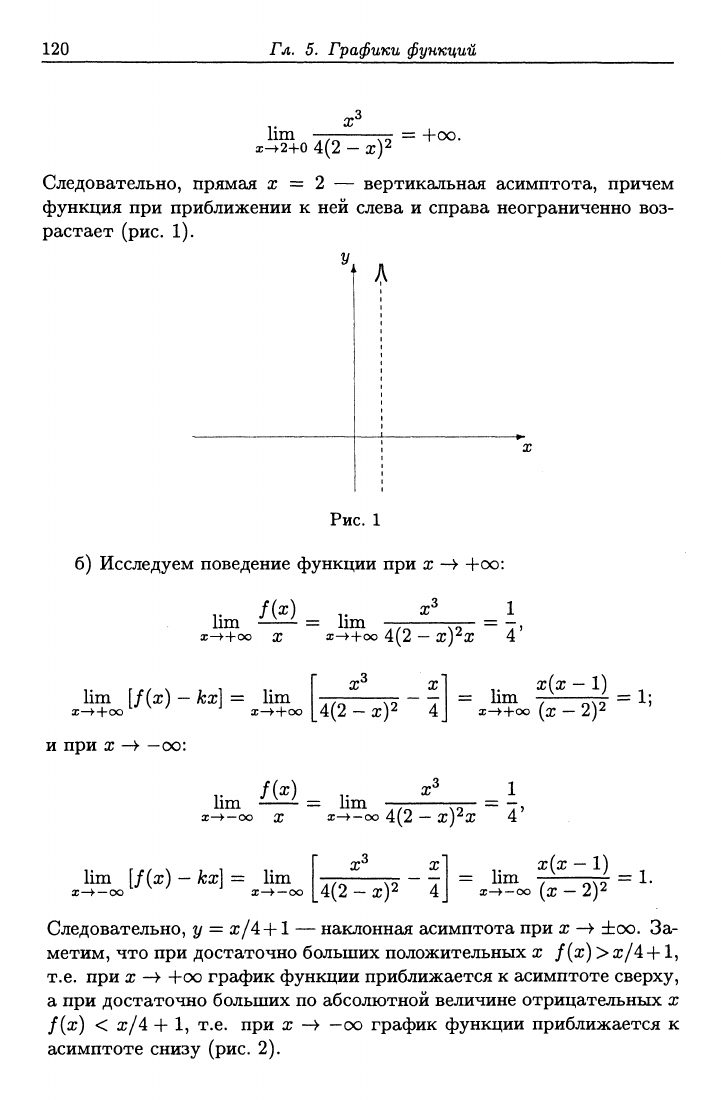
Следовательно, прямая х = 2 — вертикальная асимптота, причем

функция при приближении к ней слева и справа неограниченно воз-

растает (рис. 1).

"• л

Рис.

б) Исследуем поведение функции при х -> +оо:

х^

х->+оо X

lim \f(x)

—

кх] = lim

х-^+оо 4(2 - х)2ж 4'

"^^ '*-^ х{х

—

4(2 - хУ 4

lim

+00 {х - 2)2

= 1;

и при X

—>

—оо:

lim

х->-оо X х->-оо 4(2 — Х^Х 4

lim [f{x)

—

/гж] = lim

4(2 - хУ 4

ж(а: - 1)

ит -р -гг- = 1.

->-оо (ж - 2)^

Следовательно, 2/ = ж/4-f-1 — наклонная асимптота при х

—>

±оо. За-

метим, что при достаточно больших положительных х f{x)

а:/4+1,

т.е.

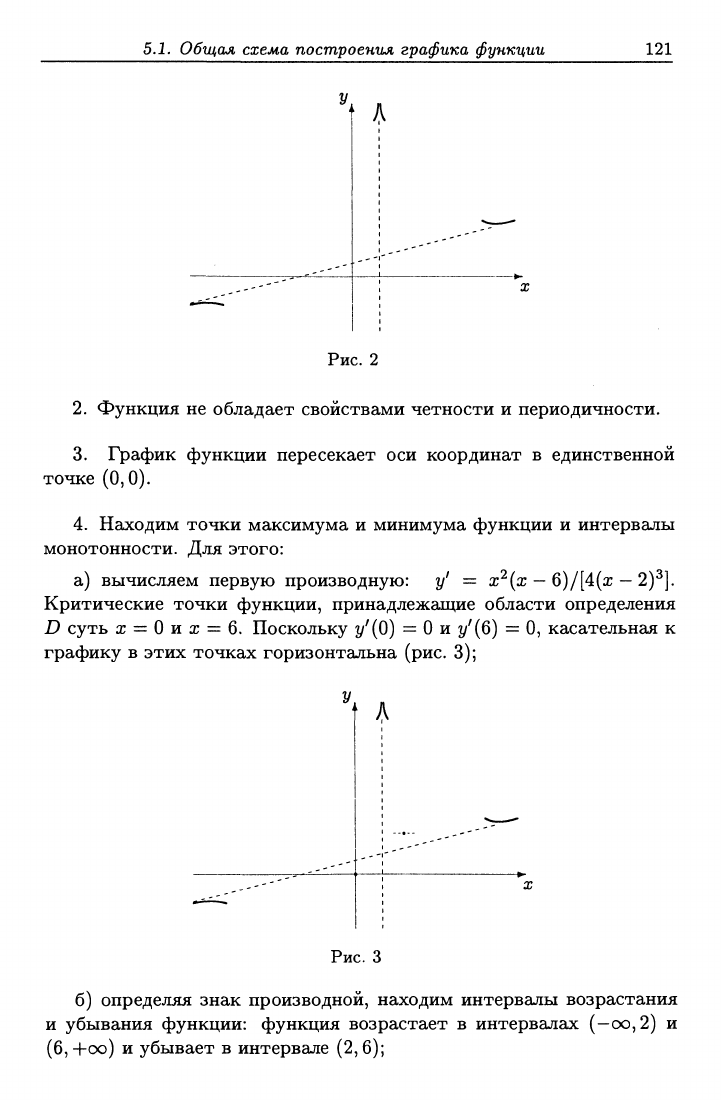
при X -^ -f-oo график функции приближается к асимптоте сверху,

а при достаточно больших по абсолютной величине отрицательных х

f{x) < х/А -h 1, т.е. при X

—>

—00 график функции приближается к

асимптоте снизу (рис. 2).

5.1.

Общая схема построения графика функции

121

Рис.

Функция не обладает свойствами четности и периодичности.

График функции пересекает оси координат в единственной

точке (0,0).

Находим точки максимума и минимума функции и интервалы

монотонности. Для этого:

а) вычисляем первую производную: у' = х^{х

—

6)/[4(ж

—

2)^].

Критические точки функции, принадлежащие области определения

D суть ж =

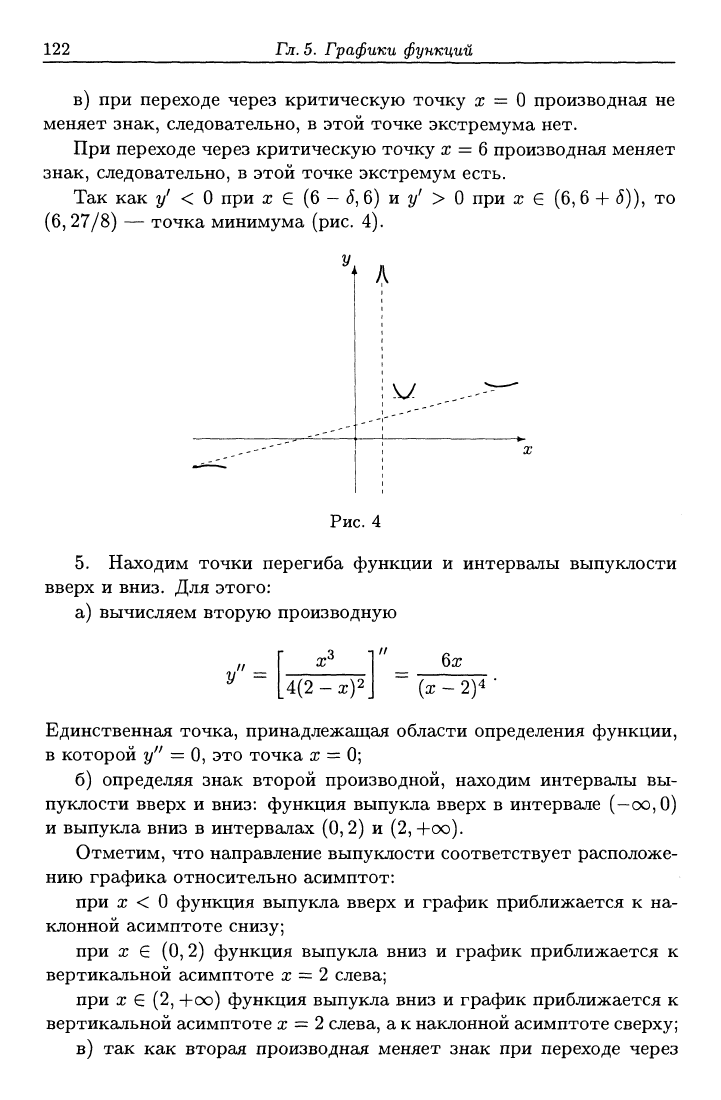
и ж = 6. Поскольку у'{0) =

и у'{6) = О, касательная к

графику в этих точках горизонтальна (рис. 3);

-^"

[ )

Рис.

б) определяя знак производной, находим интервалы возрастания

и убывания функции: функция возрастает в интервалах (—ос, 2) и

(б,+оо) и убывает в интервале (2,6);

122

Гл.

Графики функций

в) при переходе через критическую точку х — О производная не

меняет знак, следовательно, в этой точке экстремума нет.

При переходе через критическую точку х = 6 производная меняет

знак, следовательно, в этой точке экстремум есть.

Так как у' <

при ж G (6

—

6) и 2/' >

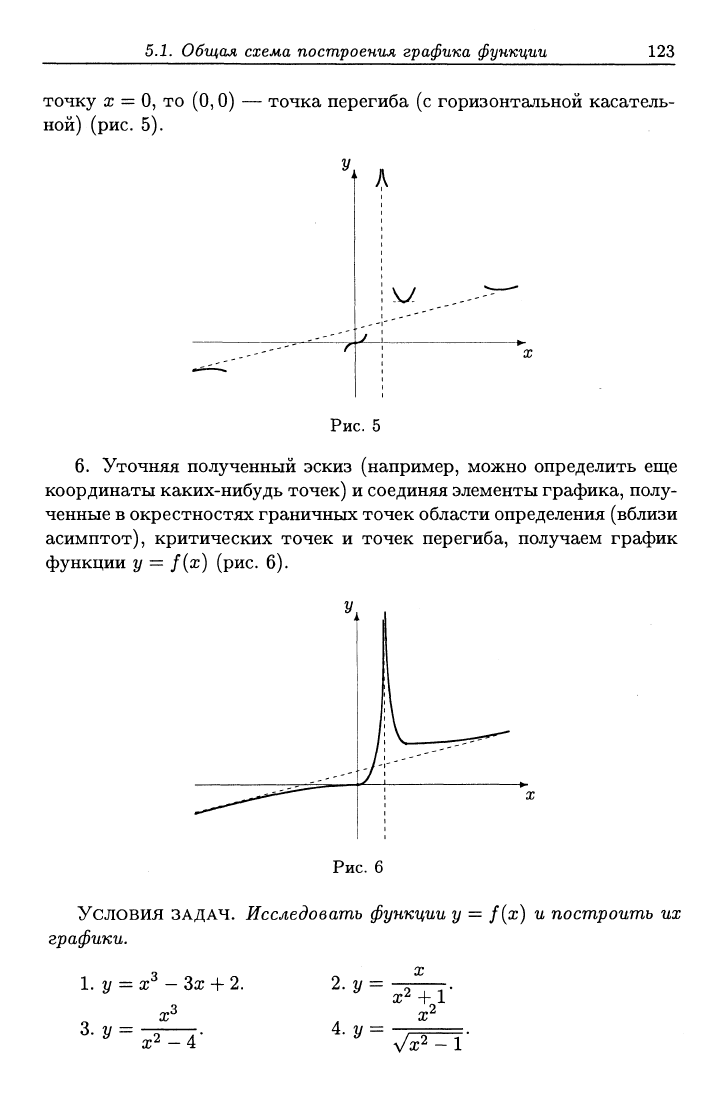
при ж G (6, 6 + 5)), то

(6,

27/8) — точка минимума (рис. 4).

—^

' А

Рис.

Находим точки перегиба функции и интервалы выпуклости

вверх и вниз. Для этого:

а) вычисляем вторую производную

4(2 - хУ

бх

{x~2Y

Единственная точка, принадлежащая области определения функции,

в которой у'' =

это точка х

б) определяя знак второй производной, находим интервалы вы-

пуклости вверх и вниз: функция выпукла вверх в интервале (—оо,0)

и выпукла вниз в интервалах (0,2) и (2, +оо).

Отметим, что направление выпуклости соответствует расположе-

нию графика относительно асимптот:

при X < О функция выпукла вверх и график приближается к на-

клонной асимптоте снизу;

при X G (0,2) функция выпукла вниз и график приближается к

вертикальной асимптоте х ~ 2 слева;

при X е (2, -foo) функция выпукла вниз и график приближается к

вертикальной асимптоте х = 2 слева, а к наклонной асимптоте сверху;

в) так как вторая производная меняет знак при переходе через

5.1.

Общая схема построения графика функции

123

точку ж = о, то (о, 0) — точка перегиба (с горизонтальной касатель-

ной) (рис. 5).

Рис.

6. Уточняя полученный эскиз (например, можно определить еще

координаты каких-нибудь точек) и соединяя элементы графика, полу-

ченные в окрестностях граничных точек области определения (вблизи

асимптот), критических точек и точек перегиба, получаем график

функции у = f(x) (рис. 6).

Рис.

Условия ЗАДАЧ. Исследовать функции у = f{x) и построить их

графики.

1.у = х''-Зх + 2.

А.у

у/^^-\

124 Гл.

Графики функций

Б. у = хе ^. 6. 1/ = —.

— 1 X

7.у =

1п

+ 1. 8.у = -—.

X тх

9. у

—

In cos

ж.

10. у — \/х'^{х

-\-1).

Ответы. 1. Асимптот нет. Точки: минимума (1,0), максимума

(-1,4), перегиба (0,2).

Асимптоты: горизонтальная j/ = 0. Точки: минимума

(-1,-1/2), максимума (1,1/2), перегиба (0,0), (-\/3,-\/3/4),

(v/3,V3/4).

Асимптоты: вертикальные х = —

х = 2, наклонная у = х.

Точки: минимума (2\/3,3\/3), максимума (—2\/3, —3\/3), перегиба

(0,0).

Асимптоты: вертикальные ж = —

а: = 2, наклонные у = —х

(при X -> —оо), у = X (при X

—>

+оо). Точки минимума (—л/2,2),

(v/2,2).

Асимптоты: горизонтальная у = О (при а; -> +оо). Точки:

максимума (1,1/е), перегиба (2,2/е^).

6. Асимптоты: вертикальная ж = О, горизонтальная у =

(при

а:

—>•

—оо). Точка минимума (1,е).

Асимптоты: вертикальные ж = О, а; = 1, горизонтальная

у = 1 (при

—>•

±оо).

8. Асимптоты: вертикальная а: = 1 (ж =

асимптотой не явля-

ется).

Точки: минимума (е, е), перегиба (е^,е/2).

9. Асимптоты: вертикальные х = 7г/2 +

тгк.

Точки максимума

(27гА:,0)

(А:

= 0,±1,...).

10.

Асимптоты: наклонная у =

ж4-1/3.

Точки: минимума (0,0),

максимума (-2/3,-^/3), перегиба (-1,0).

5.2. Наиболыпее и наименыпее

значения функции

ПОСТАНОВКА ЗАДАЧИ. Найти наибольшее и наименьшее значе-

ния функции f{x) на отрезке [а, 6].

ПЛАН РЕШЕНИЯ. Наибольшее и наименьшее значения непрерыв-

5.2. Наибольшее и

наименьшее

значения функции 125

ной функции /(ж) на данном отрезке [а,

Ь]

достигаются в критичес-

ких точках функции (точках, в которых f'{x) = О, ±оо или f'{x) не

существует) или на концах отрезка [а,

Ь].

Проверяем, что заданная функция на данном отрезке является

непрерывной.

Ищем производную заданной функции.

Находим критические точки функции f{x) и выбираем из них

те,

которые принадлежат данному отрезку [а,

6].

Вычисляем значения функции в критических точках внутри от-

резка и значения функции на концах отрезка. Сравнивая полученные

значения, находим наибольшее М и наименьшее т значения функции

на [а,

6].

ПРИМЕР. Найти наибольшее и наименьшее значения функции

Юж

+ 10

^~ ж2 +

2а;

-h 2

на отрезке [—1,2].

РЕШЕНИЕ.

Заданная функция является непрерывной на отрезке [—1,2], так

как является отношением непрерывных функций со знаменателем, не

равным нулю (ж^ -f 2ж + 2 > 0).

Вычисляем производную заданной функции:

у'^-10,

^' + '^

(a;2-f2x-f 2)2*

Критическими точками заданной функции являются ж = О и

X = —2. Данному отрезку

[—1,2]

принадлежит только точка х = 0.

Вычисляем значение функции в точке х =

и значения функции

на концах заданного отрезка. Имеем

/(0) = 5, /(-1) = 0, /(2) = 3.

Сравнивая эти значения, заключаем, что наименьшее значение

функции m = О достигается в точке х = —

а наибольшее значе-

ние М = 5 — в точке X = 0.

Ответ. Функция принимает наименьшее значение m =

в точке

ж =

—1,

а наибольшее значение М = 5 — в точке х = 0.

126

Гл.

Графики функций

Условия ЗАДАЧ. Найти наибольшее и наименьшее значения

функции у = f{x) на отрезке [а,Ь].

2/ = 1- ^а;2 - 2х,

[0,2].

y = 2x-3\^, [-1,1].

у =

х^{х-2)\

[0,2].

2/= (ж^ - 9а;2)/4 + бх - 9,

[0,4].

2/ = 4x2/(3+ х2), [-1,1].

6. у = 1+^х^ + 2х, [-2,0].

у = 2x3 - За;2 - 4,

[0,2].

8. 2/ = 3^(а:-3)2-2а; + 6,

[2,4].

9. у = ^х2(а: - 2)2,

[0,2].

10.

у = 2 - 12а;2 - 8жЗ, [-2,0].

Ответы. 1. m = у(0) = у(2) = 1, М = у(1) = 2. 2. m = у(-1) =

= -5, М = у(0) = 0. 3. m = у(0) = у(2) = О, М = у(1) = 1.

m = у(0) = -9, М = у(2) = -4. 5. m = у(0) =: О, М =

= 2/(-1) = 2/(1) = 1- 6. m = у(-2) - у(1) = 1, М - у(-1) = 2.

m =: у(1) =- -5, М = у(2) = 0. 8. m = у(3) = О, М = у(2) = 5.

9. m - у(0) = у(2) = О, М = у(1) = 1. Ю. m = у(-1) = -2,

М = у(-2) = 18.

5.3.

Исследование функции с помощью

производных ВЫСП1ИХ порядков

ПОСТАНОВКА ЗАДАЧИ. Исследовать функцию у

—

f{x) в окрест-

ност.и точки х

—

а с помощью производных высших порядков.

ПЛАН РЕШЕНИЯ. Пусть при некотором fc > 1

/'(а) = /"(а) = ... =

f^'-'Ha)

= О,

f^'Ha)

ф 0.

5.3. Исследование функции с помощью производных высших порядков 127

Тогда если к — четное число, то точка а является точкой экстремума,

а именно точкой максимума, если

f^^\a)

< О, и точкой минимума,

если /^^(а) > 0. Если же к — нечетное число, то точка а является

точкой перегиба.

ПРИМЕР. Исследовать функцию

у = sin^(a:

—

ж^ 4- 2ж

в окрестности точки а = 1 с помощью производных высших порядков.

РЕШЕНИЕ.

Вычисляем производные заданной функции в точке а = 1:

у'

= sin(2x - 2) - 2д; -f 2, у'{1) = О,

у"

cos(2x - 2) - 2, у"{1) = О,

2/'"

= -4sin(2x-2), У'"(1) = 0,

у""

= -8cos(2a: - 2), 2/""(1) = -8 < 0.

Так как к =

— четное число и

у""{1)

< О, то точка а = 1 есть

точка максимума функции у = sin^(a:

—

ж^ + 2х.

Ответ. Функциия у = sin^(a;

—

а:^ + 2ж имеет максимум в

точке а = 1.

Условия ЗАДАЧ. Исследовать функцию у = f{x) в окрестности

точки X = а с помощью производных высших порядков.

y = 2x'^-\-8x + Acos{x-\-2), а = -2.

у = 41па; + 2ж2-8ж + 5, а = 1.

?/= 2х - ж^+ со8^(ж - 1), а = 1.

у = 21п(х - 2) +

ж^

- 8х + 3, а = 3.

2/=:x^ + 8ж + 8-2e^+^ а =-3.

6. 2/ = 2cos(a:-f 3) + ж2+ 6ж + 2, а =-3.

2/ = х2 +

1-2х1п(ж

+ 1), а = 0.

S. у = sin^

- ж^ -f 4, а = 0.

128

Гл.

Графики функций

9. J/ = 2е^-2 -

ж^

+ 2а; -М, а = 2.

10.

у = 2е^ - sin

- х^ - ж, а = 0.

Ответы.

1. а = — 2 — точка минимума.

3. а

== 1

— точка минимума.

5. а = — 3 — точка перегиба.

а = О — точка максимума.

9. а =

— точка перегиба.

а =

— точка перегиба.

а = 3 — точка перегиба.

6. а = — 3 — точка максимума.

8. а =

— точка максимума.

10.

а = О — точка перегиба.

Глава б

ФУНКЦИИ НЕСКОЛЬКИХ

ПЕРЕМЕННЫХ

При изучении темы ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

вы на примерах познакомитесь с понятиями частных производных,

полного дифференциала, градиента, производной по направлению и

научитесь их вычислять. Вы также научитесь дифференцировать

сложные функции нескольких переменных и функции, заданные не-

явно.

Эти умения вы сможете применить для нахождения касатель-

ной плоскости и нормали к поверхности и точек экстремума функции

двух переменных.

С помощью пакета РЕШЕБНИК.ВМ вы можете вычислить част-

ные производные, решить системы уравнений (для нахождении ста-

ционарных точек), выполнить все численные расчеты и проверить

правильность полученных вами результатов.

6.1.

Частные производные

ПОСТАНОВКА ЗАДАЧИ. Найти частные производные до второго

порядка включит,елъно функции z = /(xi, Ж2,..., Жп).

ПЛАН РЕШЕНИЯ.

Чтобы найти частную производную функции z = /(xi,..., Хп)

по переменной Xk, фиксируем остальные переменные и дифференци-

руем / как функцию одной переменной Xk-

Частные производные высших порядков вычисляются анало-

гично последовательным дифференцированием, т.е.

5^/

дх1

9X29X1

дх\ \dxij '

fdf\

dxi \dx2J '

9^/

dxidx2

dxl ~

dx2 \dxi

д (af\

dx2 \dx2J