Zuo-Guang. Ye Advanced Dielectric Piezoelectric and Ferroelectric Materials: Synthesis, Characterisation and Applications

Подождите немного. Документ загружается.

Handbook of dielectric, piezoelectric and ferroelectric materials420

observations agree, in particular the extensive observation of phase mixing

in this system as well as in others is in opposition with prediction of second-

order phase transition, also the possibility of triclinic phase was not observed.

It should also be mentioned that no direct transitions Pm → Pm3m or Cm →

Pm3m have been observed in any system. Also the question of multiple

points should be examined more in detail in further studies: for instance to

answer the question of how the cubic–tetra–rhombo–monoclinic regions are

connected.

14.4.2 From local polar order to long-range order:

monoclinic phase as adaptive phase

In Section 14.3.3, it has been proposed from diffuse scattering experiments

that the elastic accommodation between the CORs and the PNRs is realised

via a monoclinic short-ranged zone, which is also in agreement with the

% phase

100

= 0.415

I II III IV

P4mm

Pm3m

0 100 200 300 400 500 600 700 800

(K)

= 0.43

= 0.45

= 0.50

= 0.55

Pm+P4mm

P4mm

490 K

550 K

465 K 565 K

420 K

585 K

590 K

Pm3m

(K)

14.20

Temperature evolution of the phase coexistence for some PSN–

PT compounds.

WPNL2204

From the structure of relaxors to the structure of MPB 421

structural data described in Section 14.3.1. Thus, on the mesoscale (i.e. few

nanometres) the monoclinic order may be considered as an adaptive phase

and serves as a ‘bridge’ between the CORs and the host-matrix. This local

and embedded monoclinic phase previously reported on relaxor-based systems

has also been observed by TEM on the non-relaxor PZT system (Glazer

et al., 2004) and in PMN–PT35% (Wang et al., 2006).

The progressive ‘growing’ of monoclinic phase when doping by Ti in

PMN–PT, PSN–PT or PZN–PT can be easily detected in diffraction experiments

through the observation of continuous widening of H00 peaks (which are

single in the rhombohedral patterns). In fact as already pointed-out, local

monoclinic order is detected even in the pure compounds, except that the

correlation length of the associated local polarisation appears to be higher in

PZN than in PMN, whereas weak Ti doping is needed in PSN to observe

such widening.

The notion of an adaptive phase first developed for martensitic

transformation was proposed by Khachaturyan et al. (1991) and Jin et al.

(2003) to explain the transformation pathway through the monoclinic phase

and associated features such as the tweed-like domain patterns observed in

MPB systems. The adaptive phase is issued from martensitic-like phase

transitions and is based on stress-accommodating twinned domains in a

similar way to the mesoscale structure proposed through the investigation of

the anisotropic diffuse scattering.

Some authors have also proposed that the different monoclinic phases of

MPB systems are in fact nothing other than tetragonal or rhombohedral

twinned nanodomains. A long time ago, such an idea was successfully used

in the field of incommensurate and quasicrystal systems, leading to debates

about the real existence of (for instance) five-fold (pentagonal) symmetries

or nano-twinning of six-fold twins. It appears in the end that both types of

system exist, i.e. ‘true’ incommensurate or quasicrystal systems and ‘ersatz’

nanotwinned commensurate or crystal. Perhaps the same situation will be

disclosed in the field of MPB. This is left for further studies.

14.4.3 Modelling of MPB phase diagrams

The origin of the term ‘morphotropic phase boundary’ is related to the

experimental observation of optimal properties in a restricted range of

concentration where two phases, rhombohedral and tetragonal, were supposed

to coexist. From this point of view the existence of monoclinic structures

appeared as a simpler way to rotate the polarisation; however, the discovery

that several monoclinic phases can exist and moreover coexist, also with the

rhombohedral or tetragonal phase involved, showed that the reality is in fact

rather complex. From a simplistic thermodynamic point of view the coexistence

of three phases is possible only at a definite and unique composition at

WPNL2204

Handbook of dielectric, piezoelectric and ferroelectric materials422

which an abrupt change of structure is supposed to happen when the

composition is changed. As pointed out by Rossetti et al. (2006), the diagrams

shown on Figs. 14.16 to 14.18 with abrupt boundaries cannot be equilibrium

phase diagrams and their geometry, with or without consideration of an

adjacent low-temperature monoclinic phase, contradicts thermodynamics:

according to the Gibbs phase rule, the single-phase fields on the phase diagram

must be separated by two-phase regions rather than by line boundaries. A

low-order Landau expansion in the approximation of the theory of regular

solutions by these authors showed that the phase coexistences appear to be

an equilibration process implicated by the thermodynamic. These questions

have been discussed in detail in PSN–PT by Haumont (2004).

The success of the phenomenological theory based on Landau–Devonshire

development had proved very successful in the field of magnetic and structural

phase transitions, well before the discovery of the MPB phases. The problem

of higher complexity, such as incommensurate systems for instance, has

been explained within this theoretical framework. Therefore an interpretation

of the phase diagram of PZT based on a eighth-order development of free

energy by Vanderbilt and Cohen (2001) quickly followed the experimental

report by Noheda et al. (1999). Local-density approximation (LDA) calculation

by Fu and Cohen (2000) was published the same year. The different paths of

rotation between the different possible phases have been studied and

synthetically condensed in figures such as Fig. 14.15, eventually involving

possible triclinic phase if twelfth-order polynoms are taken into account.

The main results of these works have been very briefly discussed above.

In connection with the experimental studies of the structures of MPB

diagrams we would like also to report some works from Bellaiche and

coworkers based on effective Hamiltonian calculation which have clarified

the problem of chemical versus polar order as discussed in this paper. Initially

the first system studied using these techniques was PZT (Bellaiche et al.,

2000). The results on PSN–PT (Haumont et al., 2003, 2006a) were published

later. The progressive ‘growing’ of monoclinic phase when doping by Ti in

PMN–PT, PSNPT or PZN–PT can be easily detected in diffraction experiments

through the observation of continuous widening of H00 peaks (which are

single in the rhombohedral patterns) (Fig. 14.21). Interestingly the first

principles simulations for disordered PSN–PT were unable to mimic the

observed path: only the M

phase was observed in the simulations among all

possible monoclinic phases. Moreover, it happened that the width of the

MPB obtained in the simulation was much smaller than that measured. Since

the disorder is responsible for the introduction of strong random fields,

which modify the ground state, it seems obvious that a deviation from a

perfectly homogeneous and disordered state should be realised. Simulations

made for different ordered states (some of them unrealistic!) showed other

interesting results; in particular the appearance of the M

phase (Fig. 14.22).

WPNL2204

From the structure of relaxors to the structure of MPB 423

Another result from these simulations is that none of the theoretically

investigated ordered alloys has a rhombohedral ground state at compositions

with low Ti content: they all rather adopt a monoclinic phase at low temperature.

In fact, the simulations showed that the existence of chemically ordered

Intensity arb. units

300

250

200

150

100

50.0

= 0

= 0.10

= 0.18

= 0.26

= 0.35

39 39.5 40 40.5 41 41.5

2θ (°)

0.550

0.500

0.450

0.400

0.350

0.300

0.250

0.200

0.150

0.100

FWHM (°)

R3m

0.0 0.050 0.10 0.15 0.20 0.25 0.30 0.35 0.40

14.21

X-ray rocking-curve of (200) peak in PSN–PT and associated

FWHM.

WPNL2204

Handbook of dielectric, piezoelectric and ferroelectric materials424

clusters inside the disordered matrix is needed to widen the Ti-poor part of

the calculated MPB and thus to mimic the experimental observations. For

low Ti content this heterogeneous state leads to the appearance of a

rhombohedral phase.

These simulations explain the strong connection between chemical

composition at a local scale and polar states. It is probable that the same

Local polarisation magnitude

Spontaneous polarisation (µC/cm

)

R-phase

-phase

T-phase

0.40 0.41 0.42 0.42 0.44

Ti composition

(a)

Spontaneous polarisation (µC/cm

)

R-phase

- phase

T-phase

0 200 400 600 800 1000

Temperature (K)

(b)

C-phase

-phase

14.22

Spontaneous polarization as predicted by the Heff approach:

(a) versus composition in disordered PSN–PT at

= 50K; (b), versus

temperature in PSN–PT41 for ordered structure.

WPNL2204

From the structure of relaxors to the structure of MPB 425

scenario exists in other MPB systems as very similar polarisation path is

observed.

In fact these considerations arising from modelling allows the MPB systems

to be divided in two groups. The first group includes homogeneous systems

such as PZT in which no chemical order (CORs) has been observed and for

which the MPB is confined in a restricted concentration range, in direct

agreement with the results from simulations. Others are the relaxor-based

morphotropic systems such as PMN–PT characterised by the existence of

CORs and huge regions of concentration in which monoclinic order is detected.

A further example, among the BiBB′O

–PT systems (Suchomel and Davies,

2004) is BiScO

–PT (Eitel et al., 2004; Chaigneau et al., 2007) which illustrates

the ideas that homogeneous systems exhibit a confined MPB region, with a

unique monoclinic phase. However, in this distinction one has to take care

about the scale that is considered: indeed in PZT very short chemical order

(the first core shell around Zr or Ti) was considered in first-principles calculation

which clearly shows that the very local order may also strongly affect the

ground state (George et al., 2003).

14.4.4 From CORs to chemical inhomogeneity regions

(CIRs) in the MPB phase diagrams

It is known that doping PMN or PSN with PbTiO

results in the suppression

of the short-range chemical order (CORs) as is evidenced by the continuous

decrease of intensity and correlation length of the superstructure (SS) peaks

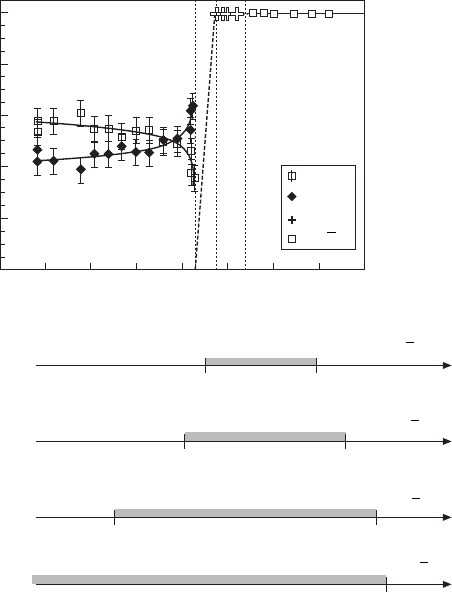
associated with cation chemical ordering. In PSN–PT (Fig. 14.23) with about

10% of titanium concentration, no more chemical ordering could be detected

but as SS factor peaks are also intrinsically diminished when Ti content is

increased, even in a perfectly ordered situation, Raman scattering experiments

are more accurate: indeed we were able to follow the local ordering of Sc/Nb

cations up to x = 0.16 concentration, a value above which no more ordering

is observed. However, we also observed the vanishing of dielectric relaxation

at concentrations far from x = 0.16 i.e. x = 0.485, just inside the MPB (Fig.

14.23) in contradiction to the mechanism of relaxation based on the interaction

of PNRs with CORs.

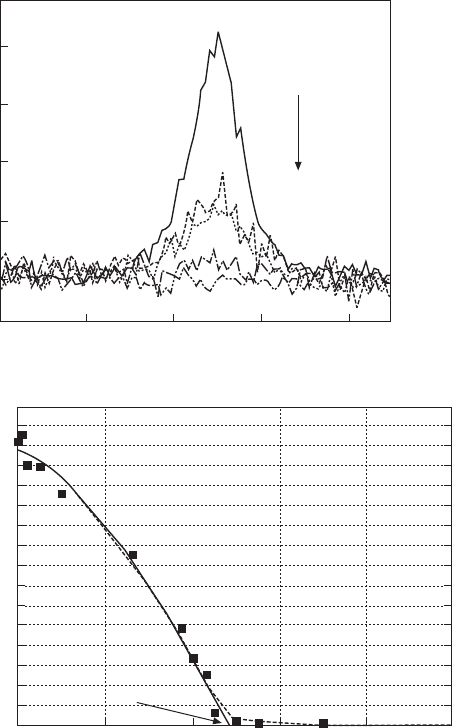
The same type of contradiction appears if one compares the concentration

evolution of the diffuse scattering in PMN–PT, associated with elastic

accommodation of PNRs with CORs which disappears between 0.25 and

0.30 (Fig. 14.24) whereas the dielectric relaxation is observed at least up to

x = 0.40, inside the MPB. These sets of observation seem to indicate that the

local ordering of Mg/Nb/Ti or Sc/Nb/Ti is not exactly the correct parameter

to consider for a global picture of relaxation and MPB in lead-based systems.

Disappearance of local ordering in PSN–PT well before the MPB

composition is reached is corroborated by the measurements of hysteresis

WPNL2204

Handbook of dielectric, piezoelectric and ferroelectric materials426

loops of polarization in disordered and long-annealed samples of PSN–PT,

whereas for low concentration of titanium, difference in the P = F(E) evolution

between both types of samples is found, and above x = 0.16 no difference

exists. The same result is obtained when comparing the temperature evolution

of dielectric constant: above x = 0.16 the evolution is identical for the disordered

or long-annealed samples.

In fact, micro-Raman spectroscopy, which is very sensitive to the local

Sc/Nb/Ti arrangement of samples, shows a great variation of signal with the

Intensity arb. units

16.0 16.4 16.8 17.2 17.6

2θ(°)

(a)

= 0

= 0.01

= 0.02

= 0.05

= 0.10

∆

(K)

3.2

2.8

2.4

2.0

1.6

1.2

0.80

0.40

0.0

MPB

≈ 0.485

0 0.2 0.4 0.6 0.8 1

(b)

14.23

In PSN–PT, (a) vanishing of superstructure peaks associated to

CORs in PSN–PT; (b) concentration evolution of dielectric relaxation.

WPNL2204

From the structure of relaxors to the structure of MPB 427

location of the beam on the surface of the ceramics, indicating a great

inhomogeneity of the Ti/Sc/Nb occupancy on the B-site of the perovskite. A

comprehensive Raman study of PSN–PT as a function of Ti content shows

that, on a local scale, heterogeneities exists up to 80% of PT (Haumont et al.,

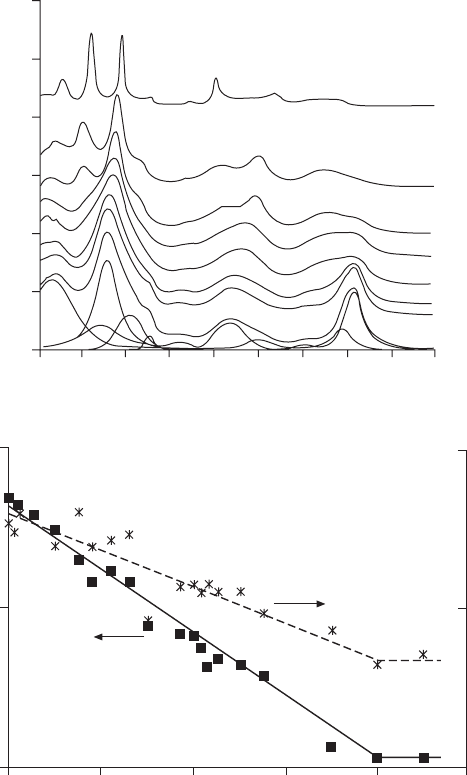
2006a). The most striking feature in the Raman spectra (Fig. 14.25) arises

from the evolution of the relative intensity defined as I

/(I

+ I

), where I

and I

are intensities of band K (or G) and band J (or H), respectively. The

value of this ratio, continuously decreases and changes close to x = 0.80. In

the PMN–PT system, the similar band K disappears at about the same Ti

content (Ohwa et al., 2001) and is a signature that a true tetragonal symmetry

is recovered above this concentration.

(b)

(d)

(a)

(c)

14.24

(

0) sections of the room-temperature X-ray precession patterns

of the PMN–PT solid solutions with differerent lead titanate content.

WPNL2204

Handbook of dielectric, piezoelectric and ferroelectric materials428

Below x = 0.80 the Raman spectral evolution presented on Fig. 14.25 can

be described on the basis of the so-called two-mode behaviour which was

also proposed for the PMN–PT system (Chaabane et al., 2004). In this two-

mode scenario the vibration modes associated with band J and band K do not

Intensity (arb. units)

2.5

1.5

0.5

(1LO), E(2TO)

E(2TO, 2LO), B

(2TO)

B(2LO)

E(3TO)

(3LO)

F(4LO)

100 200 300 400 500 600 700 800 900 1000

Wavenumber (cm

–1

)

(a)

= 1

= 0.7

= 0.55

= 0.43

= 0.37

= 0.15

= 0.05

= 0

)

0.5

0 0.20 0.40 0.60 0.80 1

(b)

0.5

)

14.25

(a) Room-temperature Raman spectra of PSN–PT powder

samples with various titanium concentration with a representative

deconvolution for pure PSN in insert. (b) Ti-dependence of the

relative intensity of band K (or G) and band J (or H).

WPNL2204

From the structure of relaxors to the structure of MPB 429

couple, that involves the existence of local phase segregation. The origin of

those bands should be due to alternation of zones richer in one constituent

than the other, with band J being associated with a very local segregation of

Ti-rich regions whereas band K corresponding to Mg/Nb-rich ones. These

local chemical orders would occur on the scale of a couple of unit cells

making them difficult to be detected by diffraction probes. In the PSN–PT

system, the same situation was also considered. Further complexity arises

from the fact that band J is detected also in pure PSN, meaning that this band

cannot be explained only on the basis of Ti-rich regions but should also be

associated with the CORs.

These sets of experiments show that the structure of the CORs transforms

with PT doping, even if they are not more detectable above x ≈ 0.16 by

diffraction technique. Above this concentration it is better to call them chemical

inhomogeneity regions (CIRs) which continue to act as a nucleation centre

for PNRs.

Additional proofs were obtained by the comparison of the diffraction

pattern of a MPB sample of PSN–PT (x = 0.43) which revealed definite

changes, before and after long-term annealing, in particular in the phase

mixing ratio of monoclinic phase Pm and tetragonal P4mm phase (85% of

Pm phase in annealed sample, instead of 79%). A comparative Rietveld

analysis shows in addition changes in the monoclinic angle (90.20° after

annealing instead of 90.09°), and also in the magnitude of polarisation for

both phases (62 and 67µC/cm

after annealing instead of 55 and 57°µC/

). These experiments clearly indicate the strong effect of a chemical

rearrangement onto the ground state in the MPB region.

14.5 Stability of the MPB phases under external and

internal fields

Up to now we have mainly discussed the concentration and temperature

structural evolution of relaxors and MPB compounds. However, many potential

applications of these materials arise from the strong effect of electric field on

properties. Moreover these applications often require the use of materials in

the form of ceramics or thin films. That is why the effects of size reduction,

external pressure, substrate-induced misfit, etc., have been recently considered.

The electric field and pressure evolution of diffuse scattering have been

briefly discussed in Section 14.3.3. The object of this section is to point out

some results related to the question of phase stability.

14.5.1 Electric field effects

Pioneering works reported investigations of the non-ergodic state of PMN

under an electric field. Indeed, when the electric field is applied along the

WPNL2204