Lefebvre A.H., Ballal D.R. Gas Turbine Combustion: Alternative Fuels and Emissions

Подождите немного. Документ загружается.

50 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

transferred to the drop is now used to furnish the heat of vaporization of the

fuel. Eventually, the drop attains its steady-state temperature and the heat

supplied to the drop is used solely as heat of vaporization. This condition

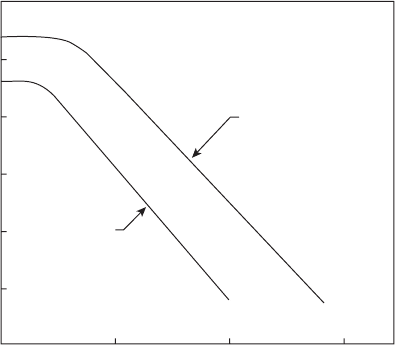
corresponds to the straight lines drawn in Figure 2.6.

2.10.1 Heat-up Period

Figure 2.6 shows the relationship between (drop diameter)

and evaporation

time for droplets of kerosine and JP 4 fuels. Inspection of this gure reveals

that the slope of the D

/t graph is almost zero in the rst stage of the evapora-

tion process and then gradually increases with time until the drop attains

its steady-state temperature, after which the value of D

/t remains fairly

constant throughout the remainder of the drop lifetime. The vaporization

curves drawn in Figure 2.6 are based on measurements carried out in air at

2000 K temperature and normal atmospheric pressure. At this pressure, the

heat-up period constitutes only a very small portion of the total evaporation

time, as indicated in Figure 2.6. However, for many fuels at high ambient

pressures and temperatures, the heat-up period is much longer; so much so

that drops formed from multicomponent fuels containing several different

petroleum compounds may not experience steady-state evaporation during

their lifetime. The practical signicance of these observations is that actual

drop and spray evaporation rates can be appreciably lower than the experi-

mental values quoted in the literature, most of which were measured during

steady-state evaporation at normal atmospheric pressure.

3.2

2.8

2.4

2.0

(Drop diameter)

, mm

1.6

1.2

0.8

Time, s

JP 4

Kerosine

Figure 2.6

Evaporation rate curves for kerosine and JP 4.

Combustion Fundamentals 51

2.10.2 evaporation Constant

One of the rst theoretical approaches to the problem of droplet evaporation

was made by Godsave [24], who derived the rate of evaporation of a single

drop as

(

)

πρλ4,

(2.16)

where

λ=

(

)

dD dt

(2.17)

Note that λ corresponds to the slope of the lines drawn in Figure 2.6.

The average rate of evaporation during the drop lifetime is obtained from

Equation 2.16 as



(

)

πρλ6.

(2.18)

The drop lifetime is also readily obtained by assuming λ is constant and

integrating Equation 2.17 gives

λ.

(2.19)

Following Spalding, the evaporation rate of a single drop can also be

expressed in terms of a mass transfer number B [25,26]. We have



mDkc B

ln 1+=

(

)

(

)

2π ,

(2.20)

whereas drop lifetime is given by

tDkc B

eFop

n1+=

(

)

(

)

81.

(2.21)

A drawback to using B instead of λ for calculating m

and t

is that the accu-

racy of the results is very dependent on the choice of values of k and c

[27].

Values of λ may be used to determine the transfer number B (and vice

versa). Equating (2.16) and (2.20) gives

λρ=

(

)

(

)

8 kc B

ln 1+ .

(2.22)

52 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

2.10.3 Convective effects

In most continuous ow combustors, the fuel is sprayed into air or gas

owing at high velocity. Where relative motion exists between the droplets

and the surrounding gas, the rate of evaporation is enhanced by forced con-

vection. This effect can be accommodated by multiplying the evaporation

rate calculated for quiescent conditions by the correction factor

1022

+ .,

where Re

, the drop Reynolds number, is typically around 5.

2.10.4 effective evaporation Constant

From a practical viewpoint, it would be very convenient if Godsave’s evapo-

ration constant, which corresponds to steady-state evaporation in quiescent

air, could be modied to take into account both the adverse effect of the

heat-up period and the benecial effect of forced convection. To accomplish

this, Chin and Lefebvre [28] dened an effective evaporation constant as

effoe

= Dt

(2.23)

where t

is the total time required to evaporate the fuel drop, including both

convective and transient heat-up effects, and D

is the initial drop diameter.

Calculated values of λ

eff

for an ambient air pressure of 100 kPa are plotted

in Figure 2.7. Similar graphs for higher levels of pressure may be found in

Chapter 5. Figure 2.7 shows plots of λ

eff

vs. T

, the normal boiling point, for

various values of UD

at three levels of ambient temperature, namely, 500,

1200, and 2000 K. While recognizing that no single fuel property can fully

describe the evaporation characteristics of any given fuel, the normal boiling

point has much to commend it for this purpose, because it is directly related

to fuel volatility and vapor pressure. It also has the virtue of being quoted in

fuel specications. Figure 2.7 shows that λ

eff

increases with increases in ambi-

ent temperature, velocity, and drop size, and diminishes with an increase in

normal boiling temperature.

For any given conditions of pressure, temperature, and relative velocity, the

lifetime of a fuel drop of any given size is obtained from Equation 2.23 as

eoeff

λ ,

(2.24)

while the average rate of fuel evaporation is given by



FFeffo

(

)

πρλ6.

(2.25)

Combustion Fundamentals 53

The velocity term U in Figure 2.7 denotes the relative velocity between

the drop and the surrounding gas. Small droplets rapidly attain the same

velocity as the surrounding gas, after which they are susceptible only to

the uctuating component of velocity, u′. For gas turbine combustors, where

the value of u′ is usually high enough to affect evaporation rates, U in

Figure 2.7 should be replaced with u′.

420 440 460 480

, K

∞

= 500 K

∞

= 1200 K

∞

= 2000 K

(m/s)(µm)

10000

5000

2000

1000

500

200

100

10000

5000

2000

1000

500

200

100

10000

5000

2000

1000

500

200

100

P = 100 kPa

1.6

1.4

1.2

1.0

0.8

0.6

1.0

0.8

0.6

eﬀ

, mm

0.4

0.2

0.24

0.20

0.16

0.12

0.08

0.04

500 520 540 560

Figure 2.7

Variation of effective evaporation constant with normal boiling point at normal atmospheric

pressure. (From Chin, J.S. and Lefebvre, A.H., Proceedings of the 20th Automotive Technology

Development Contractor Coordination Meeting, 325–31 1982.)

54 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

The concept of an effective value of evaporation constant concept has

many useful practical applications. For example, Equation 2.29 may be used

to calculate fuel spray evaporation rates in a combustion zone, whereas

Equation 2.24 greatly facilitates calculations on the length of duct required

for complete evaporation of the fuel spray when injected into a ducted air-

stream. The drop diameter selected for insertion into Equation 2.24 should,

of course, be that of the largest drop in the spray.

2.10.5 Spray evaporation

For a volume of air, V, containing n fuel drops of Sauter mean diameter D

the average rate of fuel evaporation can be expressed as



mnD

FFeffo

(

)

πρλ6.

(2.26)

The fuel/air ratio in the volume is obtained as

qnDV=

(

)

πρ ρ6

Fo A

(2.27)

which may be rewritten as

nVDq=

(

)

(

)

(

)

πρρ

AF o

(2.28)

Substituting for n from Equation 2.28 into Equation 2.26 yields



mVqD

FAeffo

=ρ λ

(2.29)

This equation gives the average rate of evaporation of a fuel spray.

More detailed information on single drop and spray evaporation, includ-

ing the effects of evaporation on drop-size distributions in sprays, may be

found in Lefebvre [27].

2.10.6 Some recent Developments

Progress in the modeling of droplet vaporization up to 1994 has been

reviewed by Peng and Aggarwal [29]. Their review includes the methodolo-

gies currently available for representing droplet motion and vaporization his-

tory in two-phase ow computations. More recent work includes a numerical

study of two-component droplet evaporation by Stengele et al. [30]. This work

is of special interest for gas turbine applications because it features gas tem-

peratures of 800 and 2000 K and a range of pressures from 1 to 40 bars.

As a further advance on the λ

eff

concept [28], Chin has developed more

sophisticated models for the evaporation of multicomponent fuel drops

Combustion Fundamentals 55

that employ variable nite mass and thermal diffusivity. This work has

culminated in a practical engineering calculation method for commercial

gas turbine fuels. The procedures employed by Chin are too detailed for

inclusion here, thus for further information, reference should be made to the

original publications [31–33].

2.11 Ignition Theory

Most ignition theories are based on the idea that the transient ignition source,

usually an electric spark, must supply sufcient energy to the combustible

mixture to create a volume of hot gas that just satises the necessary and suf-

cient condition for propagation, namely, that the rate of heat generation just

exceeds the rate of heat loss.

The work of Lewis et al. [34–36] did much to clarify and improve knowledge

of spark ignition in quiescent mixtures. The rst major contribution to ignition

theory for owing mixtures was made by Swett [37], who studied the inu-

ence on ignition energy of variations in pressure, velocity, equivalence ratio,

and turbulence. Swett’s theory is based on the ideas that (1) only a portion

of the discharge length is important in the ignition process and (2) heat loss

by thermal conduction is negligible compared with heat loss by eddy diffu-

sion. Both of these ideas were fully conrmed in subsequent experiments

carried out by Ballal and Lefebvre on ignition in owing mixtures [38,39].

Unfortunately, Swett’s treatment of turbulence is very limited and much of

his experimental data are suspect for reasons discussed in Reference [39].

2.11.1 gaseous Mixtures

Ballal and Lefebvre [38] analyzed the processes governing the rate of heat

generation in an incipient spark kernel and the rate of heat loss by thermal

conduction and turbulent diffusion. They conclude that, for the spark kernel

to survive and propagate unaided throughout a gaseous mixture, its mini-

mum dimension should always exceed the quenching distance as expressed by

cS u

po L

−

′

(

)

016ρ .

(2.30)

for low-turbulence (u′ < 2S

) and

cS u

po T

−

′

(

)

063ρ .

(2.31)

for highly turbulent mixtures

()

′

uS 2

56 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

The minimum ignition energy E

min

is dened as the amount of energy

needed to heat to its adiabatic ame temperature, the smallest volume of gas

whose minimum dimension is equal to the quenching distance. Clearly, the

smallest volume that satises this criterion is a sphere of diameter d

, so

EcTd

min

().=

po ad q

/ρπ∆ 6

(2.32)

Substituting d

from Equations 2.30 and 2.31 into Equation 2.32 leads, respec-

tively to

kS u

min

[( .)]

()

−

′

−

524

016

∆

(2.33)

and

kS u

min

−

′

(

)









(

)

−

524

063

∆

(2.34)

The result of plotting measured values of E

min

that were obtained over

wide ranges of pressure, velocity, turbulence intensity, and mixture compo-

sition for both methane and propane fuels against values of d

as calculated

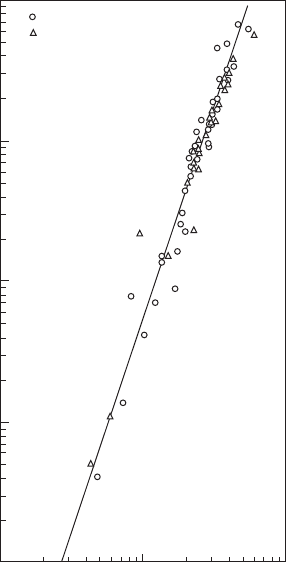
from Equations 2.30 and 2.31 is shown in Figure 2.8. The straight line drawn

through the data points has a slope of 3.0, thus conrming the cubic relation-

ship between E

min

and d

, as expressed in Equation 2.32.

The theory predicts that d

(and hence E

min

) increases with an increase in

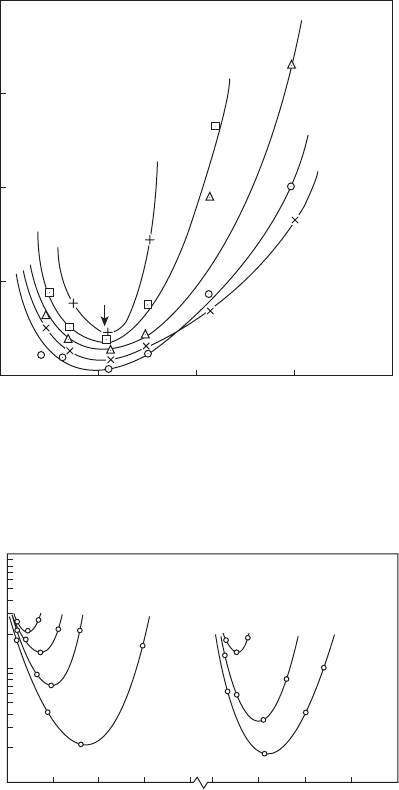
turbulence intensity; this is borne out by tests performed on propane–air

mixtures, the results of which are shown in Figure 2.9. The effect of pres-

sure on d

is illustrated in Figure 2.10. Inspection of the data points indicates

that quenching distance is roughly inversely proportional to pressure, as

predicted by Equation 2.30. This corresponds to a pressure dependence for

minimum energy of E

min

αP

–2

Figure 2.10 also illustrates the benecial effect (from an ignition stand-

point) of replacing some or all of the nitrogen in the air with oxygen.

2.11.2 Heterogeneous Mixtures

All the evidence obtained in the studies of Subba Rao, Rao, and Lefebvre

[40,41] on the ignition of owing mixtures of fuel drops and air (see

Chapter 5) serves to suggest that passage of the spark creates a kernel in

which high gas temperatures are attained, partly from the energy supplied

in the spark, but also from the heat liberated by the evaporation and rapid

combustion of the smallest fuel drops. This initial high temperature then

Combustion Fundamentals 57

falls as heat is lost by diffusion to the fresh mixture in contact with the

outside surface of the kernel, and to the remaining fuel drops undergoing

evaporation within the kernel. The key factor governing ignition is whether

these droplets can evaporate and generate heat quickly enough to counter

the heat loss from the kernel to its surroundings before it has shrunk below

its minimum critical size, which corresponds to the quenching distance for

the mixture.

When ignition is successful, combustion of the fuel vapor continues to pro-

duce heat that diffuses outward from the kernel to raise the temperature

and initiate combustion in the surrounding unburned mixture. The ame

then spreads rapidly to all regions where the air and fuel are in combustible

proportions.

Analysis of all the experimental data obtained in these investigations

[40,41] led to the conclusion that the sole criterion for the successful ignition

of mixtures of fuel drops and air is a sufciency of fuel vapor in the ignition

0.1

0.01

0.1

100

110

Quenching distance, mm

Minimum ignition energy, mJ

Slope = 3

Methane

Propane

φ = 1

P = 8.1, 18, 35.4 kPa

Figure 2.8

Relationship between E

min

and d

for both quiescent and owing mixtures. ϕ = 1.0. (From Ballal,

D.R. and Lefebvre, A.H., Proceedings of the Royal Society, London Series A, 357 (1689), 163–81, 1977.)

58 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

zone. Ignition will automatically ensue if passage of the spark creates suf-

cient thermal energy to produce the requisite amount of fuel vapor. The

basic argument is that over wide ranges of operating conditions, the chemi-

cal reaction time is so short in comparison with the time required to produce

an adequate amount of fuel vapor in the ignition zone that for all practical

0.5

Minimum ignition energy, mJ

1.0

22%

15%

2.5%

Tu rbulence

intensity

Pressure = 0.17 atmos

Velocity = 6 m/s

Fuel = propane

1.5

Equivalence ratio

2.0 2.5

Figure 2.9

Inuence of turbulence intensity on minimum ignition energy for propane–air mixtures.

(From Ballal, D.R. and Lefebvre, A.H., Fifteenth Symposium (International) on Combustion, The

Combustion Institute, Pittsburgh, PA, 1473–81, 1975.)

0.1

1.0

10.0

Pressure = 8 kPa Pressure = 35 kPa

% O

21 35

100

35 50

% O

Quenching distance, mm

10 20 30

Propane, percent volume

40 010203040

Figure 2.10

Inuence of pressure and oxygen concentration on quenching distance for propane.

Velocity = 15.3 m/s. (From Ballal, D.R. and Lefebvre, A.H., Proceedings of the Royal Society, London

Series A, 357 (1689), 163–81, 1977.)

Combustion Fundamentals 59

purposes it can be neglected [42]. This is in marked contrast to the ignition

process in homogeneous mixtures, which is totally dominated by chemical

reaction rates.

These considerations led to the development by Ballal and Lefebvre [42,43]

of a theoretical model for the prediction of quenching distance and minimum

ignition energy in liquid fuel sprays. The model is based on the assumption

that chemical reaction rates are innitely fast and that the onset of ignition is

limited solely by the rate of fuel evaporation.

The process of ignition is envisaged as occurring in the following man-

ner. Passage of the spark creates a small, roughly spherical, volume of air

(henceforth referred to as the spark kernel) whose temperature is sufciently

high to initiate rapid evaporation of the fuel drops contained within the vol-

ume. Reaction rates and mixing times are assumed innitely fast, so any

fuel vapor created within the spark kernel is instantly transformed into com-

bustion products at the stoichiometric ame temperature. If the rate of heat

release by combustion exceeds the rate of heat loss by thermal conduction

at the surface of the inamed volume, then the spark kernel grows in size

to ll the entire combustion volume. If, however, the rate of heat release is

lower than the rate of heat loss, the temperature within the spark kernel falls

steadily until fuel evaporation ceases altogether.

Thus, of crucial importance is the spark-kernel size for which the rate of

heat loss at the kernel’s surface is just balanced by the rate of heat release, due

to the instantaneous combustion of fuel vapor, throughout its volume. As

with homogeneous mixtures, this concept leads to the denition of quenching

distance as the critical size that the inamed volume must attain to propagate

unaided; the amount of energy required from an external source to attain

this critical size is termed the minimum ignition energy.

Analysis of the relevant heat-transfer and evaporation processes [42,43]

yields the following expression for the quenching distance of quiescent or

slow-moving multidroplet mists:

Ast

ln 1+

(

)













ρφ

(2.35)

It should be noted that this equation was derived through consideration of

the basic mechanisms of heat generation within the kernel and heat loss from

its surface, and it contains no experimental or arbitrary constants. It is valid

for monodisperse sprays only. However, for polydisperse sprays of the type

provided by most practical atomizing devices, it can be shown [44] that the

quenching distance is given by

Ast

ln 1+

(

)













ρφ

(2.36)