Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

C HAOS IN T WO-DIMENSIONAL M APS

Consider a point with itinerary ⭈⭈⭈S

⫺k

⭈⭈⭈S

⫺1

•

⭈⭈⭈S

⭈⭈⭈.The

image of this point under the map B has the itinerary ⭈⭈⭈S

⫺k

⭈⭈⭈S

⫺1

•

⭈⭈⭈

⭈⭈⭈. That is, the effect of the map B on itineraries is to shift the symbols one

to the left, with respect to the decimal point.

Deﬁnition 5.16 The shift map s is deﬁned on the space of two-sided

itineraries by:

s(...S

⫺2

⫺1

•

...) ⫽ ...S

⫺2

⫺1

•

....

Secondly, as we mentioned above, if the itinerary consists of a repeated

sequence of k symbols, the point is contained in a periodic orbit of period k

(or smaller). The orbit is asymptotically periodic if and only if the itinerary is

eventually periodic toward the right.

This gives us a good way to identify chaotic orbits. Any itinerary that is not

periodic toward the right is not asymptotically periodic. Recall that the Lyapunov

exponents of every orbit of the baker map are ⫺ ln 3 and ln 2, the latter being

positive. So any itinerary that does not eventually repeat a single ﬁnite symbol

sequence toward the right is a chaotic orbit.

Theorem 5.17 The skinny baker map has chaotic orbits.

5.6 THE HORSESHOE MAP

The skinny baker map has a regular construction that makes the itineraries fairly

easy to organize. Its discontinuity at the line y ⫽ 1 2 makes it less than ideal as a

model for continuous natural processes. The horseshoe map, on the other hand,

is a model that can easily be identiﬁed in continuous nonlinear maps like the

enon map.

For example, Figure 5.14 shows a quadrilateral, which we shall refer to

loosely as a rectangle, and its image under the H

enon map (2.8) of Chapter 2.

Notice that the image of the rectangle takes a shape vaguely reminiscent of a

horseshoe, and lies across the original rectangle. The dynamics that result in the

invariant set are in many ways similar to those of the baker map.

The horseshoe map is a creation of S. Smale. Deﬁne a continuous one-

to-one map h on ⺢

as follows: Map the square W ⫽ ABCD to the overlapping

horseshoe image, as shown in Figure 5.15, with h(A) ⫽ A

ⴱ

, h(B) ⫽ B

ⴱ

, h(C) ⫽

ⴱ

,andh(D) ⫽ D

ⴱ

. We assume that in W the map uniformly contracts distances

horizontally and expands distances vertically. To be deﬁnite, we could assume

216

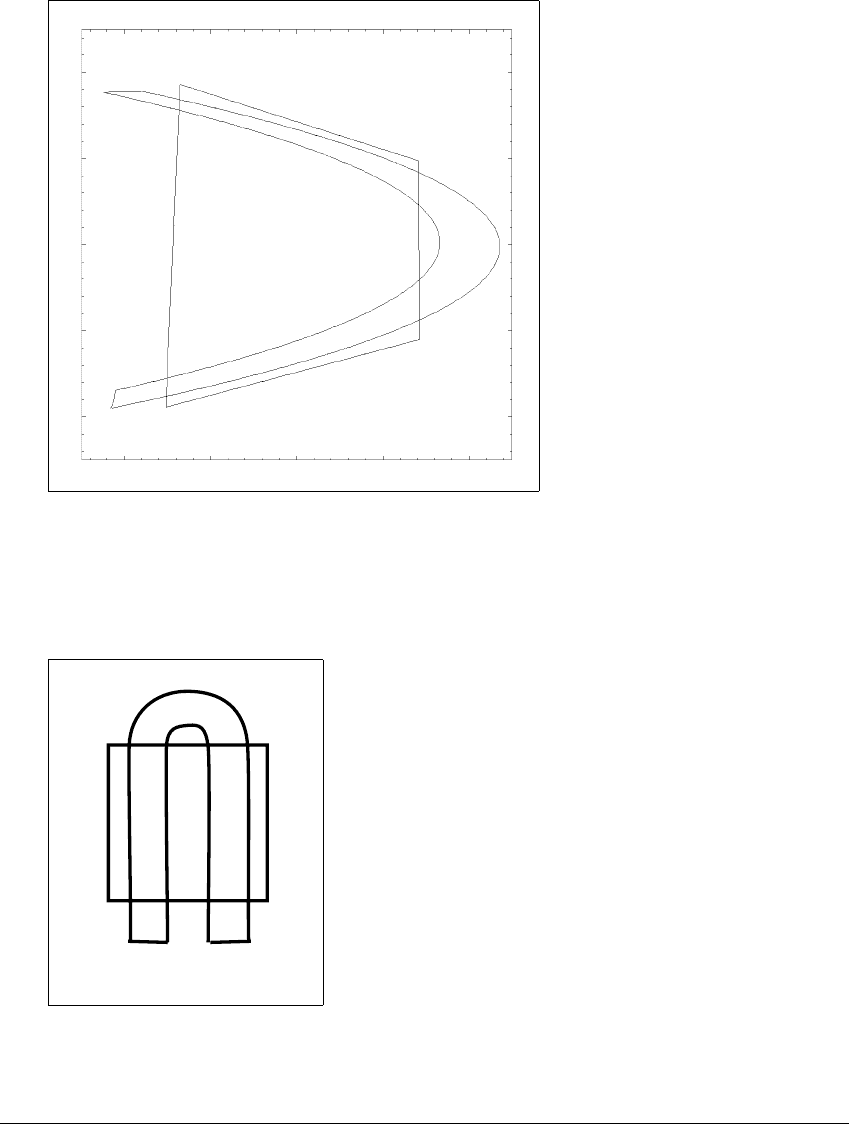
5.6 THE H ORSESHOE M AP

Figure 5.14 A horseshoe in the H

enon map.

A quadrilateral and its horseshoe-shaped image are shown. Parameter values are

a ⫽ 4.0andb ⫽⫺0.3.

A* B* C* D*

Figure 5.15 The horseshoe map.

The map sends the square W ⫽ ABCD to its image A

ⴱ

, which is shaped

like a horseshoe.

217

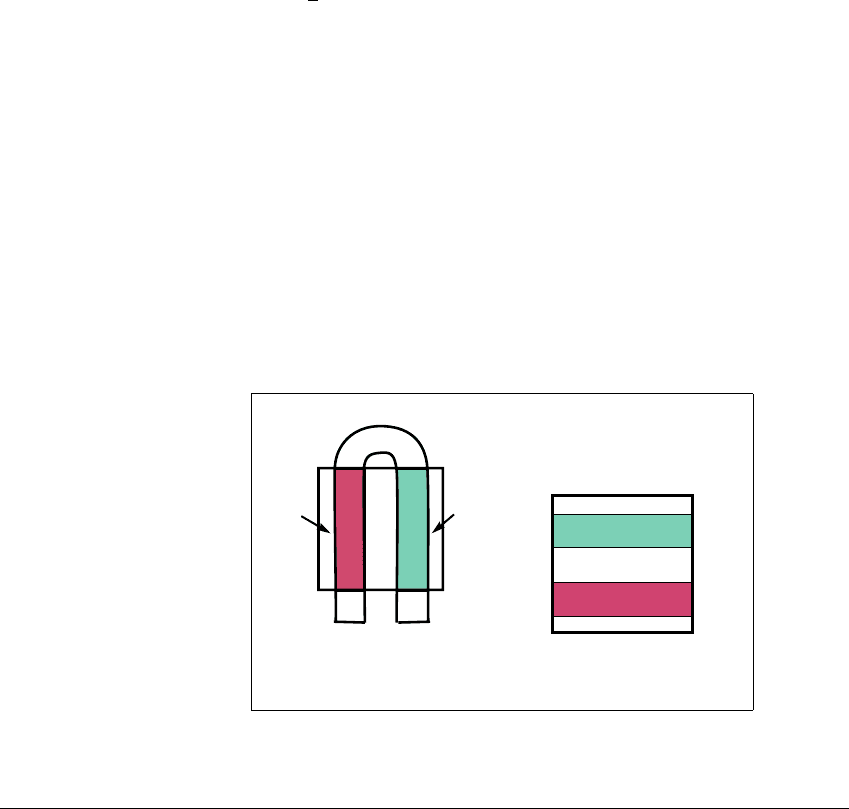
C HAOS IN T WO-DIMENSIONAL M APS

points are stretched vertically by a factor of 4, and squeezed horizontally by a

factor of 4. Outside W, the only restriction we make on h is that it be continuous

and one-to-one.

In our analysis of the horseshoe map, we focus on the points in the plane

that remain in the rectangle W for all forward and backward iterates. These points

form the invariant set H of h.

Notice that any point in H must be in either the left leg V

or the right

leg V

of W 傽 h(W). We can assign itineraries to these points that depend on

the location, V

or V

, of each iterate. As with the baker map, the itinerary that

gives the forward iterates does not uniquely deﬁne a point, and both the past and

future of a point are needed in order to identify it. For a point v in H,wedeﬁne

the itinerary

v of v to be ...S

⫺3

⫺2

⫺1

•

...,as follows:

1. If h

(v) lies in V

,setS

⫽ L.

2. If h

(v) lies in V

,setS

⫽ R.

Which points in W map into V

and which map into V

? Imagine unfolding

the horseshoe image, stretching it in one direction and shrinking it in another,

so that square A

ⴱ

can be placed exactly on square ABCD. Then the

points corresponding to V

and V

form two horizontal strips, labeled

•

L and

•

in Figure 5.16. The points in

•

L (respectively,

•

R) are those that map into V

(respectively, V

) and for which S

is L (respectively, R).

In order to assign coordinate S

, “unfold” h

(W), as shown in Figure 5.17.

The four sets of points whose itineraries begin S

form four horizontal strips,

nested in pairs inside the strips

•

L and

•

R. Again, each time we specify an

A* B*

C* D*

(a) (b)

Figure 5.16 Unfolding of the horseshoe map.

The grey (resp., black) region in (b) maps to the grey (resp., black) region in (a).

218

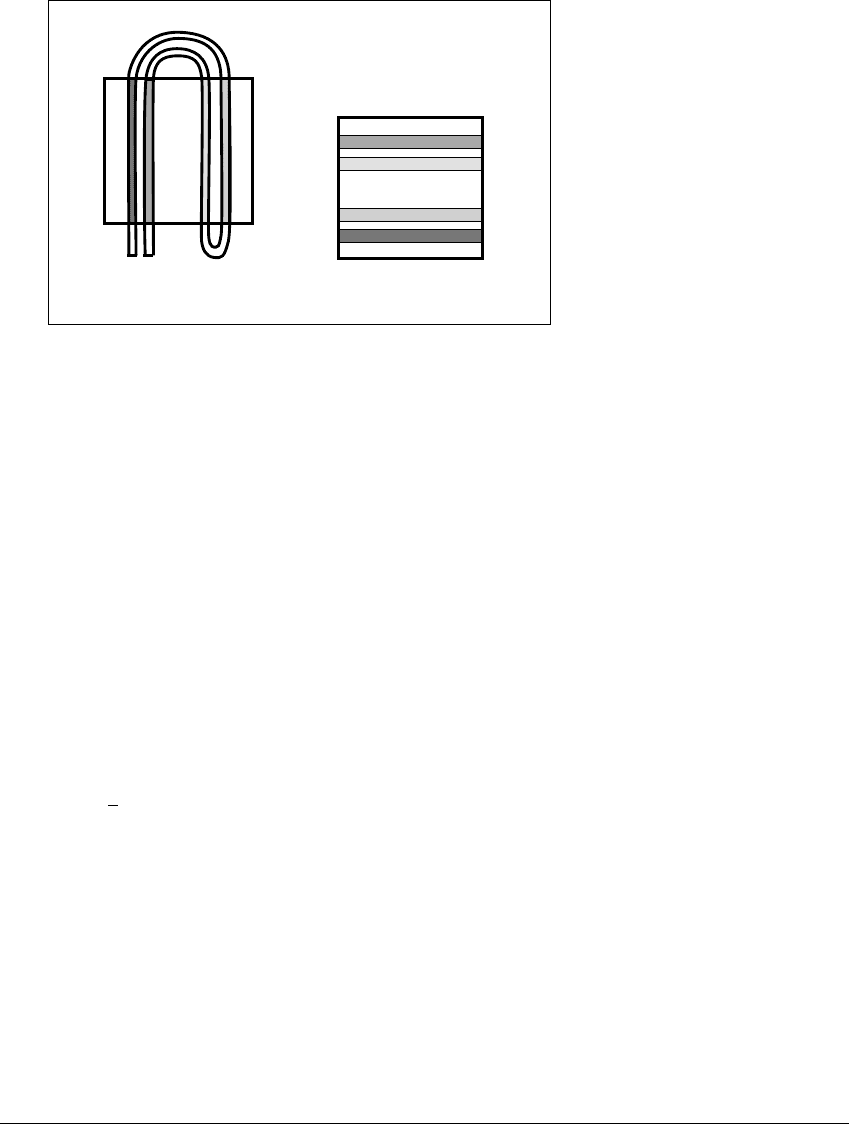
5.6 THE H ORSESHOE M AP

2 3 4

.RL

.RR

.LR

.LL

(a) (b)

Figure 5.17 Unfolding h

(

), the second iterate of the horseshoe map.

Forward itineraries of points in the unit square are shown.

additional coordinate, we double the number of horizontal strips. When the entire

sequence

•

...is speciﬁed, the set of points represented is a horizontal line

segment. The collection of these segments, for all possible such sequences, forms

a Cantor set of horizontal line segments.

Now we turn to the inverse iterates. Which points have h

⫺1

in V

and which

in V

? To begin with, if the inverse iterate of a point v in W is to remain in W,

v must be in V

or V

. If we do the inverse procedure of h, i.e., unfolding h(W),

then, as we saw previously, the inverse images of V

and V

are the horizontal

strips

•

L and

•

R. The set of points within

•

L that are in V

are labeled L

•

L in

Figure 5.18(a); those in V

are labeled R

•

L. Figure 5.18(b) shows the points v in

W for which

v has S

⫺1

•

equal to each of the four partial sequences: LL

•

, RL

•

,andLR

•

By specifying the entire one-sided sequence ...S

⫺2

⫺1

•

,werepresent

a vertical line segment of points. The collection of all such sequences is a

Cantor set of vertical line segments. To specify exactly one point in H,we

intersect the vertical line segment represented by ...S

⫺2

⫺1

•

and the hori-

zontal line segment represented by

•

.... Thus each two-sided itinerary

...S

⫺2

⫺1

•

... corresponds to exactly one point in H. Notice that an

assumption of uniform stretching in one direction and contraction in the other

is necessary for the width of the vertical strips and height of the horizontal strips

to go to zero, ensuring the one-to-one correspondence.

219

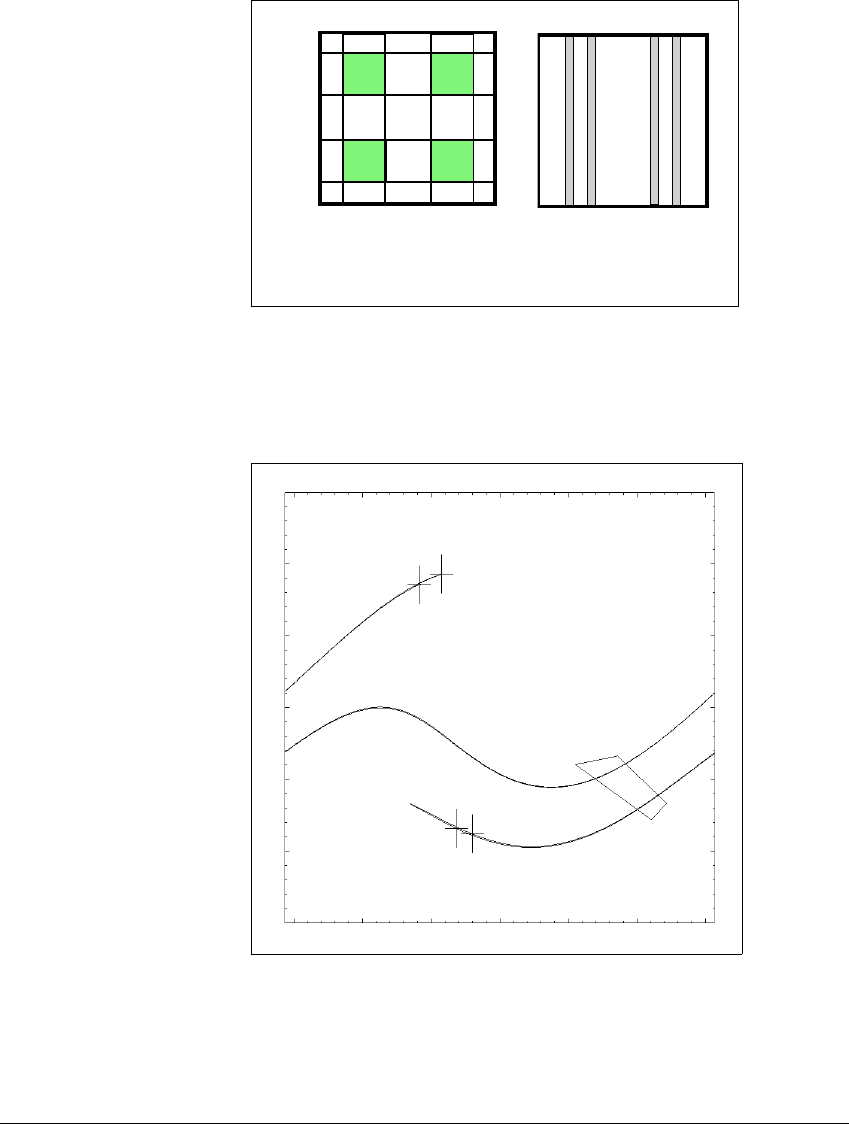
C HAOS IN T WO-DIMENSIONAL M APS

L.L R.L

L.R R.R

LL. LR. RR.RL.

(a) (b)

Figure 5.18 Itineraries of the horseshoe map.

(a) Two-sided itineraries are intersections of vertical and horizontal strips. (b) Back-

ward itineraries correspond to vertical strips.

Figure 5.19 Horseshoe in the forced damped pendulum.

The rectangular-shaped region is shown along with its ﬁrst image under the time-2

␲

map. The image is stretched across the original shape, and is so thin that it looks

like a curve, but it does have width. The crosses show the image of the corner points

of the domain rectangle.

220

5.6 THE H ORSESHOE M AP

✎ E XERCISE T5.8

Construct the periodic table for the horseshoe map, for periods up to 6.

We can also deﬁne a shift map, identical to Deﬁnition 5.16 for the baker

map. Notice that in the case of two-sided itineraries the shift map is invertible.

As with the baker map, the one-to one correspondence says in the context of

this deﬁnition that h(v) ⫽ w if and only if s(

v) ⫽ w. In particular, there are

exactly two ﬁxed points in W, whose symbol sequences are ...RR

•

RR ... and

...LL

•

LL ....

If we assume that the horseshoe map stretches and contracts uniformly

at points in the invariant set and that stretching directions map to stretching

directions and contracting directions map to contracting directions, then each

orbit in the invariant set has a positive Lyapunov exponent. For example, assume

that the horseshoe in Figure 5.15 has width 1 4 of the width of the original square

ABCD, and length three times the original. Then the Lyapunov exponents are

ln 3 and ⫺ ln 4. With this assumption, we can say the following.

Theorem 5.18 The horseshoe map has chaotic orbits.

The forced damped pendulum (2.10) of Chapter 2 also has a horseshoe.

Figure 5.19 shows a “rectangle” of initial conditions (

␪

). The long thin image

set represents the images of those states 2

␲

time units later. The corners of the

image rectangle are marked with crosses. Recall that

␪

, the horizontal variable, is

periodic with period 2

␲

, so that the image set is a connected set.

The horseshoe map of Theorem 5.18 is a prototype. To the extent that a

system such as the forced damped pendulum maps a rectangle across itself in the

shape of a horseshoe, and satisﬁes appropriate stretching and shrinking conditions,

the rich itinerary structure of the prototype horseshoe of this section will exist.

One of the most profound facts of chaotic dynamics is Theorem 10.7, due to

S. Smale, that shows that horseshoes must exist in the vicinity of any transversal

homoclinic intersection of stable and unstable manifolds.

We have seen that the existence of a horseshoe in a map forces a great

deal of complexity (a two-sided shift map) in the system dynamics. Theoretical

discovery of the horseshoe was followed by the identiﬁcation of its presence in

real systems. Color Plates 21–22 show a horseshoe in the dynamics of a laboratory

mixing apparatus along with the intricate patterns that follow.

221

C HAOS IN T WO-DIMENSIONAL M APS

☞ C HALLENGE 5

Computer Calculations and Shadowing

RE COMPUTER calculations reliable? We have shown the results of com-

puter calculations in this book to demonstrate mathematical concepts. Some

of these calculations involve many thousands of iterations of a map. Because

ﬂoating-point computers have a ﬁnite degree of precision, there will be small

errors made on essentially every operation the computer carries out. Should the

pictures we make, and conclusions we reach on the basis of computer calculation,

be trusted?

This is a deep question with no deﬁnitive answer, but we will begin with

some simple examples, and in Challenge 5 work our way to a surprisingly strong

positive conclusion to the question. We start by considering ﬁxed points, and

establish that it is certainly possible for a computer to produce a misleading

result. Let

f(x, y) ⫽ (x ⫹ d, y ⫹ d), (5.14)

where d ⫽ .000001. Consider the initial condition x

⫽ (0, 0), and suppose the

computer makes an error of exactly ⫺d in each coordinate when f is computed.

Then the computer will calculate the incorrect

f(0, 0) ⫽ (0, 0), instead of the

correct f(0, 0) ⫽ (d, d). The computer says there is a ﬁxed point but it is wrong.

The true map has no ﬁxed points or periodic points of any period.

It seems extremely easy to make such a mistake with this map—to ﬁnd a

ﬁxed point when there isn’t one. From this example one might infer that using

a computer to make mathematical conclusions about interesting maps means

trading the world of mathematical truth for “close enough”.

The problem is compounded for longer-term simulations. If k ⫽ 10

,the

correct f

(0, 0) ⫽ (1, 1) has been turned into

(0, 0) ⫽ (0, 0) by the computer.

Many small errors have added up to a signiﬁcant error.

Add to this the consideration that the above map is not chaotic. Suppose we

are using a computer to simulate the iteration of a map with sensitive dependence

on initial conditions. A digital computer makes small errors in ﬂoating-point

calculations because its memory represents each number by a ﬁnite number of

binary digits (bits). What happens when a small rounding error is made by the

computer? Essentially, the computer has moved from the true orbit it was supposed

to follow to another nearby orbit. As we know, under a chaotic map, the nearby

orbit will diverge exponentially fast from the true orbit. To make matters worse,

222

C HALLENGE 5

these small rounding errors are being made each iteration! From this point of

view, it sounds as if the computer-generated orbit is garbage, and that simulating

a chaotic system is hopeless.

The goal of Challenge 5 is to have you take a closer look, before you melt

your chips down for scrap. It is true that the orbit the computer generates will

not be the actual orbit starting at the initial value the computer was given.

As discussed above, sensitive dependence makes it impossible to do otherwise.

However, it is possible that the computer-generated orbit closely approximates a

true orbit starting from another initial condition, very close to the given initial

condition. Often it is close enough so that the computed orbit found is acceptable

for the intended purpose.

You will start with the skinny baker map B. The ﬁrst goal is to prove the

fact that if the image B(x

) lies within a small distance of x

, then there must be

a ﬁxed point near that pair of points. In other words, the baker map is immune to

the problem we saw above for map (5.14).

Step 1 Assume that B(x

) differs from x

by less than d in each coordinate.

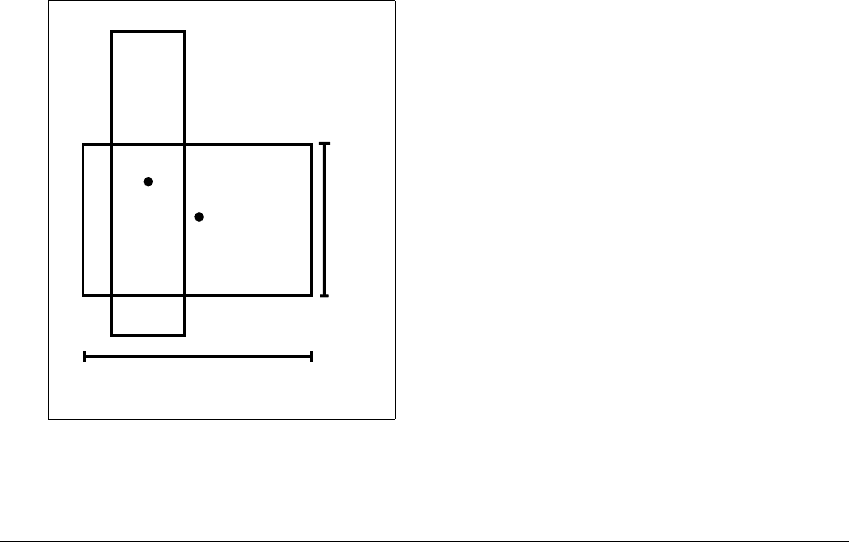
In Figure 5.20 we draw a rectangle centered at x

with dimensions 3d in the

horizontal direction and 2d in the vertical direction. Assume that the rectangle

lies on one side or the other of the line y ⫽ 1 2, so that it is not chopped in two

B(S

)

B(x

)

Figure 5.20 Image of a small square under the baker map.

The wide rectangle S

maps across itself, implying that a ﬁxed point exists in the

overlap.

223

C HAOS IN T WO-DIMENSIONAL M APS

by the map. Then its image is the rectangle shown; the center of the rectangle is

of course B(x

). Show that the image of the rectangle is guaranteed to “lie across”

the original rectangle. Explain why there is a ﬁxed point of B in the rectangle,

within 2d of x

Step 2 Now suppose our computer makes mistakes in evaluating B of size

at most 10

⫺6

, and it tells us that B(x

)andx

are equal within 10

⫺6

. Prove that

B has a ﬁxed point within 10

⫺5

of x

So far these results are less than astonishing. In order for B(x

)tomap

near x

under the baker map, x

must be either near the lower left or upper right

corners of the square. Since the two ﬁxed points are (0, 0) and (1, 1), it’s no

surprise that x

is near a ﬁxed point. The next fact, however, we ﬁnd amazing.

Step 3 Prove Theorem 5.19.

Theorem 5.19 Let B denote the skinny baker map, and let d ⬎ 0. Assume

that there is a set of points 兵x

, x

,...,x

k⫺1

, x

⫽ x

其 such that each coordinate of

B(x

) and x

i⫹1

differ by less than d for i ⫽ 0, 1,...,k⫺ 1. Then there is a periodic

orbit 兵z

, z

,...,z

k⫺1

其 such that |x

⫺ z

| ⬍ 2d for i ⫽ 0,...,k⫺ 1.

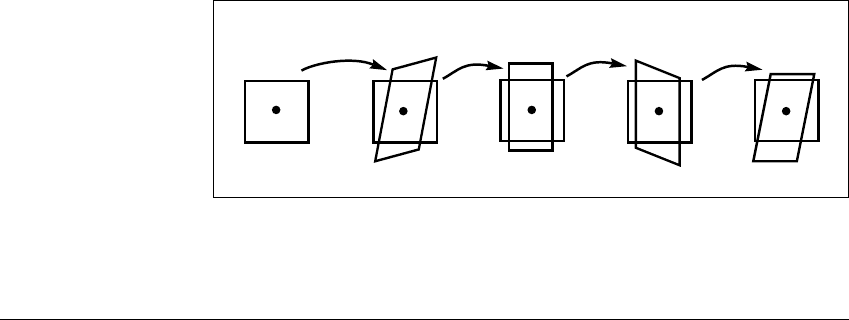
[Hint: Draw a 3d ⫻ 2d rectangle S

centered at each x

as in Figure 5.21. Show

that B(S

) lies across S

i⫹1

by drawing a variant of Figure 5.20, and use Corollary

5.13.]

Therefore, if you are computing with the skinny baker map on a computer

with rounding errors of d ⫽ .000001 and ﬁnd an orbit that matches up within

the ﬁrst seven digits, then you know there is a true periodic orbit within at

f f

Figure 5.21 Transitivity of lying across.

For the rectangle S

on the left and repeated on the right, f

) lies across S

(by

the transitivity of ‘lying across’, Figure 5.10). This implies that f

has a ﬁxed point.

224

C HALLENGE 5

most 2d ⫽ .000002. (The 2 can be replaced by the slightly smaller



13 2.)

The striking fact about the theorem is that the length of the orbit is nowhere

relevant. The theorem can be used to verify the existence of a period-one-million

orbit as well as a ﬁxed point. The true orbit that slinks along very close to a

computer-generated “approximate orbit” is called a shadowing orbit. Moreover,

the phenomenon holds even more generally than for periodic orbits.

Step 4 Let f be any continuous map, and assume that there is a set of

rectangles S

,...,S

such that f(S

) lies across S

i⫹1

for i ⫽ 0,...,k⫺ 1, each

with the same orientation. Prove that there is a point x

in S

such that f

)

lies in the rectangle S

for all 0 ⱕ i ⱕ k. By the way, does k have to be ﬁnite?

Step 5 Let B denote the baker map and let d ⬎ 0. Prove the following:

If 兵x

, x

,...,x

其 is a set of points such that each coordinate of B(x

)andx

i⫹1

differ by less than d for i ⫽ 0, 1,...,k⫺ 1, then there is a true orbit within 2d of

the x

, that is, there exists an orbit 兵z

, z

,...,z

其 of B such that |x

⫺ z

| ⬍ 2d

for i ⫽ 0,...,k.

Step 6 To what extent can the results for the baker map be reproduced

in other maps? What properties are important? Show that the same steps can

be carried out for the cat map, for example, by replacing the 3d ⫻ 2d rectangle

appropriately.

Step 7 Assume that a plot of a length one million orbit of the cat map

is made on a computer screen, and that the computer is capable of calculating

an iteration of the cat map accurately within 10

⫺6

. Do you believe that the dots

plotted represent a true orbit of the map (to within the pixels of the screen)?

Step 8 Decide what property is lacking in map (5.14) that allows incorrect

conclusions to be made from the computation.

Postscript. Computer-aided techniques based on Challenge 5 have been used to

verify the existence of true orbits near computer-simulation orbits for many different

systems, including the logistic map, the H

enon map, the Ikeda map, and the forced

damped pendulum (Grebogi, Hammel, Yorke, Sauer, 1990). For these systems, double-

precision computations of orbits of several million iterates in length have been shown to

be within 10

⫺6

of a true orbit, point by point. Therefore, the computer pictures shown in

this book represent real orbits, at least within the resolution available to the printer which

produced your copy. Astronomers have begun to apply shadowing ideas to simulations

of celestial mechanics in order to investigate the accuracy of very long orbits of n-body

problems (Quinn and Tremaine, 1992).

225