Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

C HAOS IN T WO-DIMENSIONAL M APS

E XERCISES

5.1. Assume that the map f on ⺢

has constant Jacobian determinant, say det Df(x) ⫽ D

for each x. Explain why the product of all m Lyapunov numbers is D (equivalently,

the sum of the Lyapunov exponents is ln D).

5.2. Let





⫽







(mod 1).

Then f is deﬁned on the unit square in

⺢

(or on the torus). Find the Lyapunov

exponents of any orbit of the map. Notice that these numbers are exactly half those

of the cat map of Example 5.4. Why?

5.3. Show that the cat map of Example 5.4 is one-to-one.

5.4. Draw the transition graphs for the Markov partitions of the skinny baker map and

the horseshoe map.

5.5. Show that the set of chaotic orbits of the horseshoe map is uncountable.

5.6. Show that the invariant set of the horseshoe map contains a dense chaotic orbit.

5.7. Consider the map f(z) ⫽ z

,wherez represents complex numbers.

(a) Use Euler’s formula from complex arithmetic to show that f corresponds to

the map p(r,

␪

) ⫽ (r

, 2

␪

) in polar coordinates.

(b) Find all initial points whose trajectories are bounded and do not converge

to the origin.

(a) (b)

Figure 5.22 Images of the unit square.

The maps used in Exercise 5.8. (a) The image of the unit square intersects itself in

two pieces, and (b) in three pieces.

226

E XERCISES

(d) Show that f has chaotic orbits.

5.8. Explore itineraries and periodic points for the two maps deﬁned on the unit square

shown in Figure 5.22. For each map, decide in what ways it is similar to, and different

from, the horseshoe map. Draw and label with symbols the strips of points which

stay in the square for two forward iterates. Repeat for backward iterates. Find the

transition graph for each map, and show examples of periodic orbits.

5.9. Let f be a continuous map on

⺢

,andS a rectangle in ⺢

with vertical sides s

and

, and horizontal sides s

and s

. Assume that f(s

)andf(s

) surround s

and s

(in terms of x-coordinates) and that f(s

)andf(s

) surround s

and s

(in terms of

y-coordinates). Show that f has a ﬁxed point in S.

5.10. (from Clark Robinson) Let f(x, y) ⫽ (5 ⫺ x

⫺ 0.3y, x), a version of the H

enon map.

Deﬁne the rectangles V

⫽ [⫺3, ⫺1] ⫻ [⫺3, 3] and V

⫽ [1, 3] ⫻ [⫺3, 3]. (a) Show

that the net rotation of f on the boundary of the rectangle is nonzero, for both V

and V

. (b) Show that 兵V

其 is a Markov partition for f. (c) What periods are

present in the periodic orbits of f?

227

C HAOS IN T WO-DIMENSIONAL M APS

☞ L AB V ISIT 5

Chaos in Simple Mechanical Devices

NE OF THE most appealing properties of chaos is the fact that it is exhibited

by systems on a wide variety of size scales, including scales within the ﬁrst-

hand experience of human beings. One of the most familiar physical systems,

to anyone who has used a swing as a child or watched a grandfather clock, is

the pendulum. We have already used a mathematical model of the pendulum to

illustrate concepts. The equation for the forced, damped pendulum apparently

has chaotic trajectories, as shown by a plot of its time-2

␲

map in Figure 2.7 of

Chapter 2.

Here we present two experiments which were carried out jointly by the

Daimler-Benz Corporation, which has a long-term interest in mechanical sys-

tems, and a nearby university in Frankfurt, Germany. Both start with a simple

mechanical system, and apply periodic forcing. These nonchaotic elements com-

bine to produce chaos. The researchers built a mechanical pendulum that could

be forced externally by torque at its pivot, and a metal ribbon whose oscillations

can be forced by placing it in an alternating magnetic ﬁeld. Both exhibit chaotic

orbits in a two-dimensional Poincar

e map.

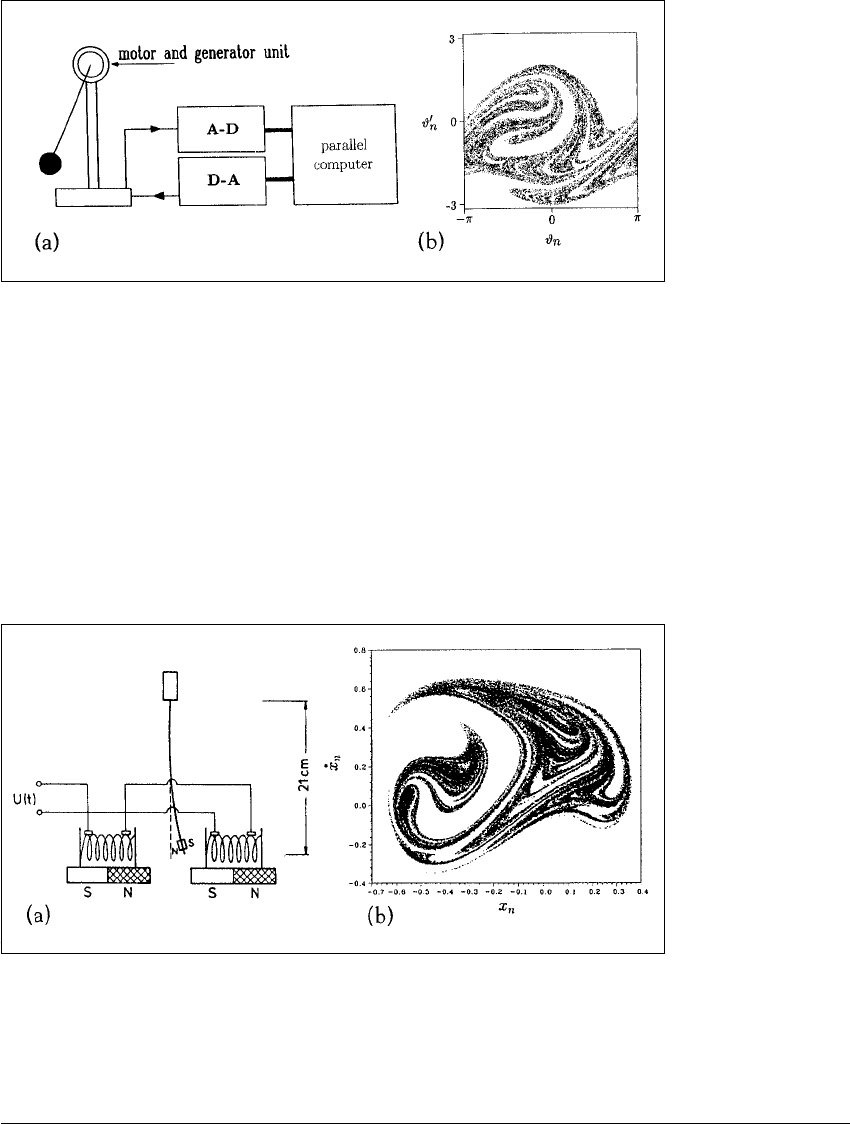
Figure 5.23(a) shows a schematic picture of the pendulum constucted by

the group. The damping is due to mechanical friction, and the forcing is applied

through an electric motor at the pivot point of the pendulum. The motor applies

force sinusoidally, so that the torque alternates in the clockwise/counterclockwise

direction, exactly as in Equation (2.10) of Chapter 2.

An experimental time-T map of the pendulum is shown in Figure 5.23(b).

The time T is taken to be the forcing period, which is 1.2 seconds. The plot of an

orbit of the map bears a strong resemblance to the theoretical pendulum attractor

of Figure 2.7 of Chapter 2. There are differences due to discrepancies in param-

eter settings of the computer-generated system as compared to the experimental

ubinger, B., Doerner, R., Martienssen, W., Herdering, M., Pitka, R., Dressler, U.

1994. Controlling chaos experimentally in systems exhibiting large effective Lyapunov

exponents. Physical Review E 50:932–948.

Dressler, U., Ritz, T., Schenck zu Schweinsberg, A., Doerner, R., H

ubinger, B., Mar-

tienssen, W. 1995. Tracking unstable periodic orbits in a bronze ribbon experiment.

Physical Review E 51:1845–8.

228

L AB V ISIT 5

Figure 5.23 The experimental forced damped pendulum.

(a) The experimental setup shows an electric motor at the pivot, controlled by the

computer via the digital-analog converter, provides the periodic forcing. (b) A plot

of (

␪

) done in time increments of length 1.2 seconds, the period of the forcing

torque at the pivot.

system. The fractal dimension of the time-T map in Figure 5.23(b) was estimated

to be 1.8. Since each point represents an entire loop of the trajectory, the entire

attractor should have dimension 2.8.

The second experimental setup is an elastic bronze ribbon, shown in Figure

5.24(a). Two small permanent magnets have been attached to the free end of the

Figure 5.24 The bronze ribbon experiment.

(a) Two small magnets are attached to the free end of the ribbon. Two large per-

manenet magnets provide an inhomogeneous magnetic ﬁeld, and an alternating

current through the two coils provide a periodic forcing to the ribbon. (b) An orbit

of the time-2

␲

map. One hundred thousand (x,

x) pairs are plotted.

229

C HAOS IN T WO-DIMENSIONAL M APS

ribbon. Deﬁne the variable x to be the distance of the tip from its equilibrium

position with no bend. Two larger magnets set up a magnetic ﬁeld such that

the original equilibrium x ⫽ 0 is no longer stable. Instead, there are two stable

equilibrium positions symmetrically situated about x ⫽ 0. When the oscillating

magnetic ﬁeld set up by the coils is added, there are no stable equilibria, and the

ribbon wobbles chaotically.

The period of the oscillatory voltage in the coil is 1 second in the experiment

reported here. Figure 5.24(b) shows a plot of the time-1 map for the bronze ribbon.

The fractal structure of the chaotic attractor is clearly visible.

230

C HAPTER S IX

Chaotic Attractors

N IMPORTANT aspect of explaining dynamical phenomena is the description

of attractors. Newton knew of two types of attracting motion that systems settle

into: the apple sitting on the ground is in equilibrium, and the planets in the solar

system are undergoing periodic, or more properly quasiperiodic motion, at least to

good approximation. For the next 300 years, these were the only kinds of motion

known for simple dynamical systems. Maxwell and Poincar

ewereamongasmall

number of scientists who were not content with this view. The small number

grew, but it was not until the widespread availability of desktop computers in the

last quarter of the 20th century that the third type of motion, chaos, became

generally recognized.

In previous chapters, we have developed the concept of a chaotic orbit.

We have seen they occur in certain one-dimensional quadratic maps and in

two-dimensional maps with horseshoes. But can chaotic motion be attracting?

231

C HAOTIC ATTRACTORS

If chaotic motion is to be observed in the motion of a physical system, it must

be because the set on which the chaotic motion is occurring attracts a signiﬁcant

portion of initial conditions. If an experimentalist observes a chaotic motion,

he or she has chosen (often randomly) an initial condition whose trajectory

has converged to a chaotic attractor. This motion could perhaps be described as

“stable in the large” (it attracts a large set of initial conditions) while “locally

unstable” (it is a chaotic orbit).

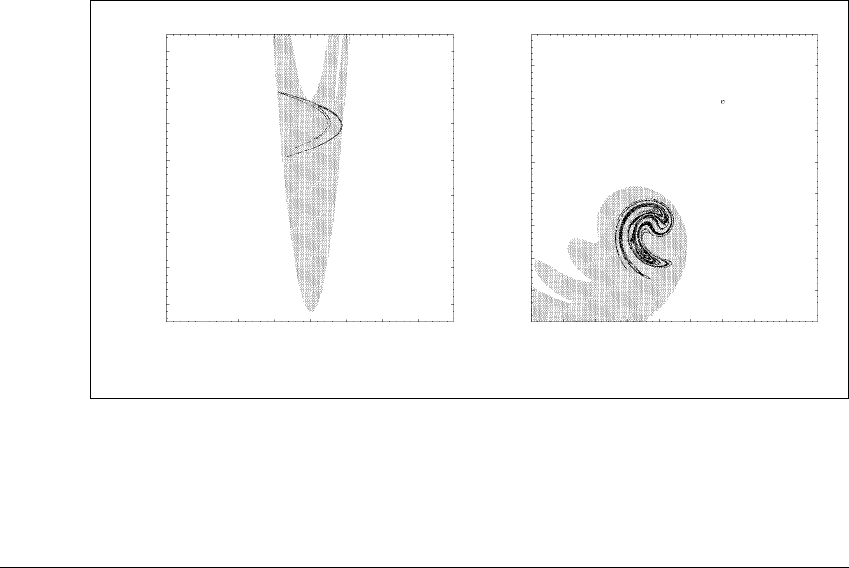
Figure 6.1 shows two numerically observed chaotic attractors. The black

set in each picture was obtained by plotting a ﬁnite trajectory that appears to

be chaotic. Throughout the calculation, the orbit appears to have a positive

Lyapunov exponent and it fails to approach periodic behavior. Figure 6.1(a)

shows a chaotic orbit (in black) of the H

enon map:

f(x, y) ⫽ (a ⫺ x

⫹ by, x), (6.1)

where a ⫽ 1.4andb ⫽ 0.3. The gray set in Figure 6.1(a) is the basin of the chaotic

orbit, the set of initial values whose orbits converge to the black set. The iteration

of any point chosen randomly in the gray region would produce essentially the

same black set—that is, after throwing out the initial segment of the trajectory

⫺11

⫺88

(a)

⫺3

⫺36

(b)

⫹

Figure 6.1 Chaotic attractors of plane maps.

Each part shows a chaotic attractor in black inside a gray basin. (a) The chaotic

attractor of the H

enon map. White points are attracted to inﬁnity. (b) The chaotic

attractor of the Ikeda map. Gray points approach the chaotic attractor; white points

approach the sink in the upper right corner at (3.00, 3.89).

232

6.1 FORWARD L IMIT S ETS

during the approach to the attractor. The white set consists of initial values whose

orbits diverge to inﬁnity.

Figure 6.1(b) shows a chaotic orbit of the Ikeda map, whose governing

equation is:

f(x, y) ⫽ (R ⫹ C

(x cos

␶

⫺ y sin

␶

),C

(x sin

␶

⫹ y cos

␶

)), (6.2)

where

␶

⫽ C

⫺ C

 (1 ⫹ x

⫹ y

), and R, C

, and C

are ﬁxed parameters.

For this picture, the settings R ⫽ 0.9,C

⫽ 0.4,C

⫽ 0.9, and C

⫽ 6 were

used. This map was proposed as a model of the type of cell that might be used

in an optical computer. The chaotic orbit is shown in black; the gray set consists

of initial values whose orbits are attracted to the chaotic orbit. The white set

consists of initial values whose orbits converge to the sink located approximately

at (3.0026, 3.8945).

The two most important properties of a chaotic attractor are demonstrated

in Figure 6.1. A chaotic attractor: (1) contains a chaotic orbit, and (2) attracts a

set of initial values that has nonzero area in the plane. Both of these properties

are fairly intuitive, but both need further elaboration to make them more precise.

6.1 FORWARD LIMIT SETS

The idea of a chaotic orbit is familiar by now. By deﬁnition, it is not periodic or

asymptotically periodic, and it has at least one positive Lyapunov exponent. Now

we introduce the idea of “chaotic attractor”, keeping in mind as our model the

black limit sets in the previous ﬁgures. First of all, a chaotic attractor is a “forward

limit set”, which we deﬁne formally below. It is in some sense what remains after

throwing away the ﬁrst one thousand, or one million, or any large initial number

of points of a chaotic orbit. That means that the orbit continually returns to the

vicinity of these points far into the future.

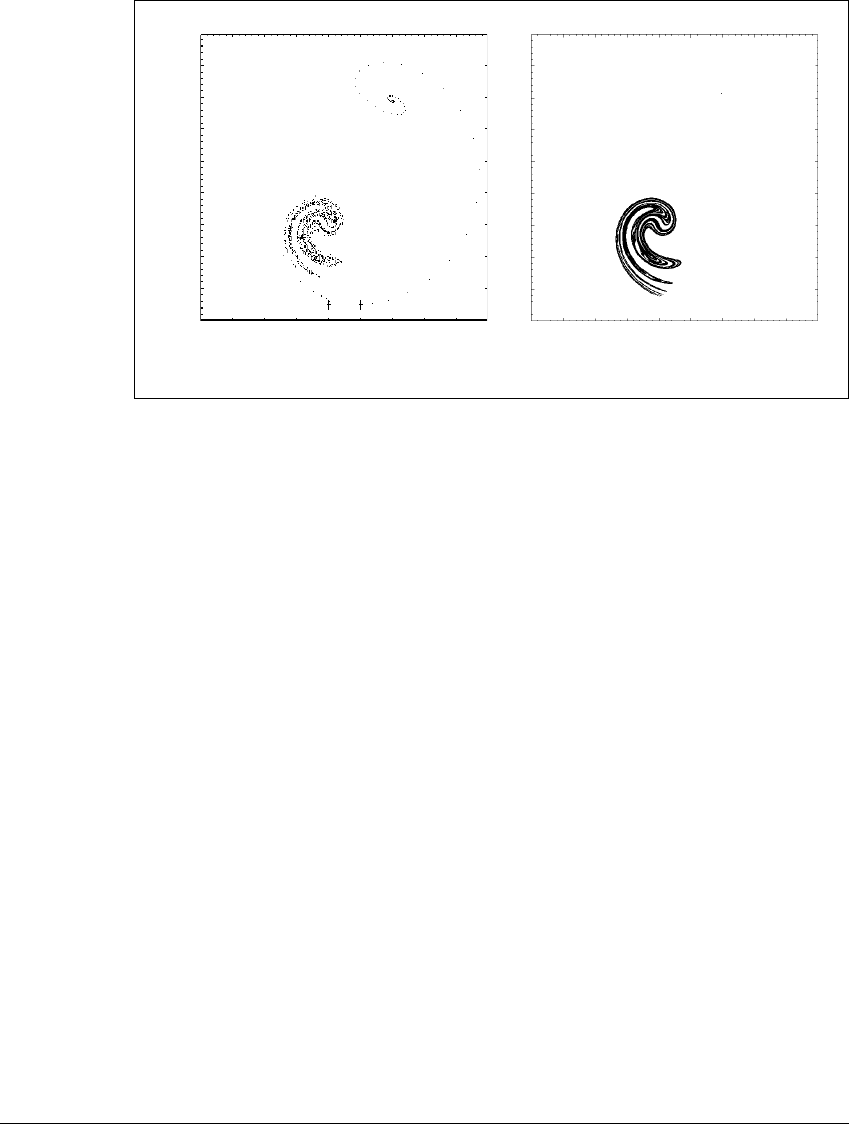
Figure 6.2(a) shows the ﬁrst 1000 points of two different orbits of the Ikeda

map. The two initial conditions are marked by crosses. The two initial values lie

in separate basins (see Figure 6.1(b)), so their orbits have different asymptotic

behavior. Figure 6.2(b) shows iterates 1,000,001 to 2,000,000 of the same two

orbits.

For one orbit, the 10

plotted points lie on the chaotic Ikeda attractor

shown in Figure 6.1(b). We predict you will see a similar picture no matter

how many iterates are thrown away (and no matter which initial condition is

chosen within the basin). This set of points that won’t go away is the forward

limit set of the orbit. In the other case, the 10

points lie on top of the sink at

233

C HAOTIC ATTRACTORS

⫺3

⫺36

(a)

⫺36

(b)

Figure 6.2 Two orbits of the Ikeda map.

(a) Two initial values are denoted by crosses. The next 1000 iterates of each initial

value are plotted. One orbit approaches the chaotic attractor, the other approaches

a sink. (b) Points 1,000,001–2,000,000 of each orbit are plotted. Part (b) shows

some points of the forward limit set of the chaotic orbit of part (a).

⬇ (3.0026, 3.8945). Higher iterates of the orbit do not return to the initial point

since the orbit becomes trapped by the sink. The forward limit set in this case is

the set consisting of the sink alone. It is an attractor but it is not chaotic.

The forward limit set of an orbit 兵 f

)其 is the set of points x to which

the orbit forever makes occasional neighborhood visits. No matter how small

⑀

⬎ 0ischosen,andnomatterhowlongN we wait, there is an n ⬎ N with

) ⫺ x| ⬍

⑀

. For example, if f

) tends toward a period-two orbit, then the

forward limit set is comprised of the two points of the periodic orbit. If x is one of

these two points, then |f

) ⫺ x| would be small only for large odd values of n

or large even values.

Deﬁnition 6.1 Let f be a map and let x

be an initial condition. The

forward limit set of the orbit 兵 f

)其 is the set

␻

) ⫽ 兵x : for all N and

⑀

there exists n ⬎ N such that |f

) ⫺ x| ⬍

⑀

其.

This set is sometimes called the

␻

-limit set of the orbit;

␻

is the Greek letter

omega, the last letter of the Greek alphabet. If

␻

) is a forward limit set of some

orbit and x

is another initial condition, then we will say that the orbit 兵 f

)其

(or the point x

)isattracted to

␻

)if

␻

) is contained in

␻

234

6.1 FORWARD L IMIT S ETS

The deﬁnition of forward limit set of an orbit is the set of points to which

the orbit returns arbitrarily close, inﬁnitely often. Points in an orbit may or may

not be contained in its forward limit set. The forward limit set may have no points

in common with the orbit, as is the case with the forward limit set of an orbit

converging to a sink. In this case the forward limit set is one point, the sink,

which is approached by the orbit as closely as you specify and as far forward in

time as you want to require. The orbit is attracted to the sink.

Fixed-points are forward limit sets because x

⫽

␻

). So are periodic

orbits, for the same reason: The forward limit set of the orbit is the orbit itself.

These are examples of ﬁnite sets, but larger sets can also be forward limit sets. In

Chapter 3, we found a chaotic orbit for the logistic map G ⫽ g

that is dense in

the unit interval [0, 1]. This orbit returns arbitrarily close inﬁnitely often to every

number between 0 and 1. Therefore the forward limit set of this orbit is [0, 1].

The fact that the chaotic orbit is dense in [0, 1] is an important one. It means

that no smaller set could be its forward limit set.

✎ E XERCISE T6.1

Show that if x

is in a forward limit set, say

␻

(y), then the entire orbit

兵 f

):n ⱖ 0其 is in

␻

(y).

✎ E XERCISE T6.2

Show that a forward limit set cannot contain a ﬁxed point sink unless it is

itself a ﬁxed point sink. Can a forward limit set contain any ﬁxed points and

be more than a single point?

Deﬁnition 6.2 Let 兵 f

)其 be a chaotic orbit. If x

is in

␻

), then

␻

) is called a chaotic set. In other words, a chaotic set is the forward limit set

of a chaotic orbit which itself is contained in its forward limit set. An attractor is

a forward limit set which attracts a set of initial values that has nonzero measure

(nonzero length, area, or volume, depending on whether the dimension of the

map’s domain is one, two, or higher). This set of initial conditions is called the

basin of attraction (or just basin), of the attractor. A chaotic attractor is a chaotic

set that is also an attractor.

The requirement that the deﬁning chaotic orbit be in its own forward limit

set ensures that a chaotic set has a dense orbit (why?), and thus provides that

the set be irreducible. We stress that not all chaotic sets are chaotic attractors, as

Exercise T6.3 shows.

235