Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems
Подождите немного. Документ загружается.


C HAOTIC ATTRACTORS
✎ E XERCISE T6.3
(a) Show that the logistic map g
a
(x) ⫽ ax(1 ⫺ x), for a ⬎ 4, has a
chaotic set, which is not a chaotic attractor.
(b) Show that the horseshoe (described in Chapter 5) contains a
chaotic set.
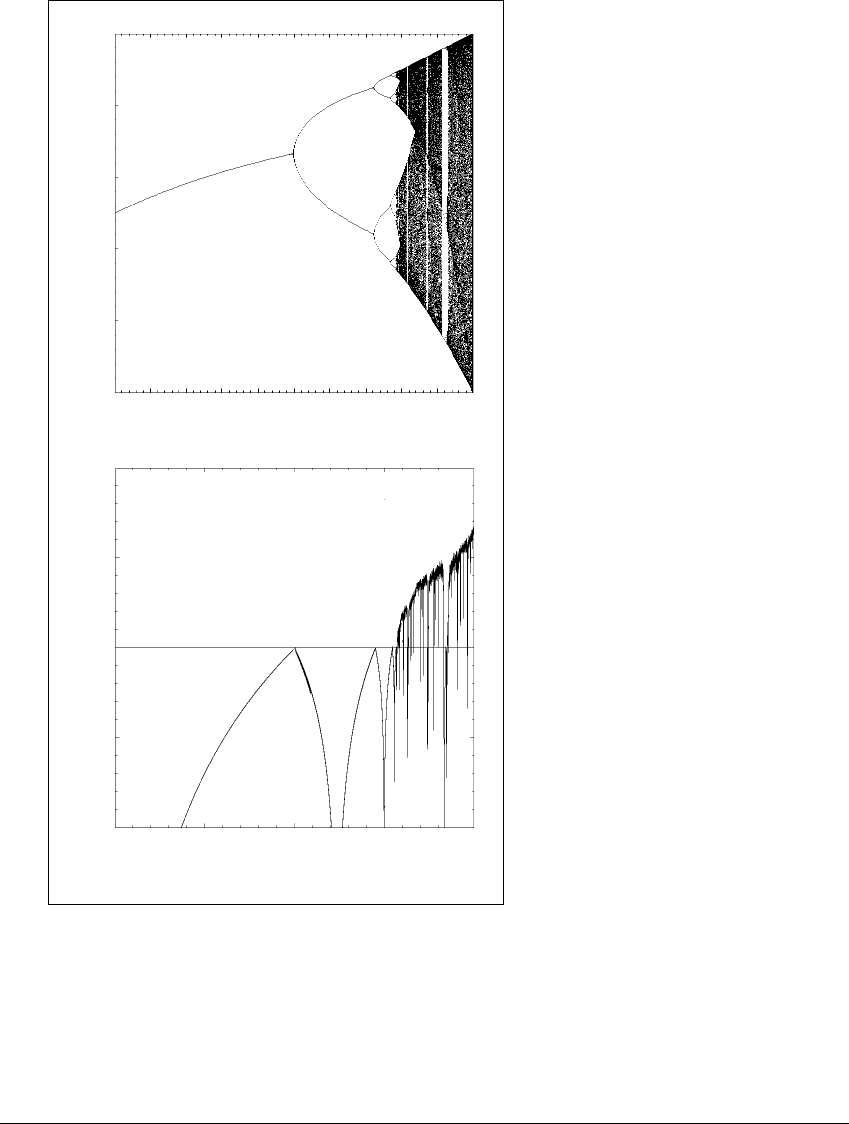
Figure 6.3 shows the observable attractors for the one-parameter family of
one-dimensional maps g
a
(x) ⫽ ax(1 ⫺ x) over a values in the range 2 to 4. Each
vertical slice of the figure is the attractor for a fixed value of a. The figure was
made as follows: for each value of a, a random initial value in [0, 1] is chosen;
the orbit of this point is calculated and the first 100 iterates are discarded. During
this time, the initial condition converges toward the attractor. The next 10,000
iterates are plotted and should reflect an orbit on (more precisely, infinitesimally
close to) the attractor.
The attractors vary widely for different values of the parameter a.When
for a given a value the chosen initial point is in the basin of a fixed point
attractor, only one point will appear in the vertical slice at that a value. This
behavior characterizes a values below 3. When the initial value is in the basin
of a periodic attractor, isolated points in the attracting orbit will appear in the
vertical slices. This behavior occurs for subintervals of a values throughout the
diagram. Beginning at a ⫽ 3, for example, there is a period-two attracting orbit,
which becomes a period-four attractor, then a period-eight attractor, etc., as the
parameter is changed. An interval of parameter values for which the only attractor
is a periodic orbit is called a periodic window in the bifurcation diagram.
For certain a values (larger than a ⫽ 3.57), one observes an entire interval
or intervals of plotted points. (Recall this is one orbit plotted.) Calculation of
Lyapunov exponents at these parameter values indicates that the orbits are indeed
chaotic. In addition, virtually every choice of initial value in (0, 1) yields the same
diagram, indicating a large basin of attraction for these sets. The last a value with
a visible limit set is a ⫽ 4. For a values larger than 4, the orbits of almost all points
in [0, 1] leave the interval and become unbounded. Although there appear to be
entire intervals of a values with chaotic attractors, looks can be deceiving, as the
Computer Experiment 6.1 shows.
➮ COMPUTER EXPERIMENT 6.1
Let g
a
(x) ⫽ ax(1 ⫺ x). Choose a subinterval of length 0.01 in the parameter
a which appears to contain only chaotic attractors (for example, a set within
236
6.1 FORWARD L IMIT S ETS
1
x
0
2a4
(a)
1
0
⫺1
2a4
(b)
Figure 6.3 Attractors and Lyapunov exponents for the logistic family of maps.
(a) Attractors of g
a
are plotted on the vertical scale. The horizontal axis is the
parameter a. (b) Lyapunov exponents of the attracting orbit of g
a
versus parameter
a. The exponent rises and hits zero at period doublings and becomes positive in the
chaotic region. It drops below 0 when there is a periodic attractor.
237

C HAOTIC ATTRACTORS
[3.9, 4.0], according to Figure 6.3(a)). Magnify the region until a periodic window
is located.
Disclaimer 6.3 This is a good place to remark on the difficulty of proving
rigorously that orbits are chaotic, even for simple systems. For a particular vertical
slice in Figure 6.3, even if the best computer approximation can indicate a positive
Lyapunov exponent and a nonperiodic orbit, this is not a mathematical proof. If
the orbit is periodic with period longer than the number of atoms in the universe,
no simple computer iteration scheme will tell us. The same caution is due for
the two attractors in Figure 6.1. Although they appear to be chaotic orbits from
computer experiments, there is at the time of this writing no rigorous proof of
that fact.
➮ COMPUTER EXPERIMENT 6.2
Choose a point p on the attractor of g
a
for a ⫽ 3.9. (Find this point by
taking the 1000th point of a trajectory in the basin.) Choose another point x in
the basin, and let m
n
be the minimum distance between p and the first n iterates
of x. Print out values of n and m
n
each time m
n
changes. Does m
n
→ 0asn →
⬁
?
Can you quantify the rate at which it goes to zero? (In other words, what is the
functional relation of m
n
and n?)
Figure 6.4 shows two other examples of probable chaotic attractors of plane
maps. In each case, the chaotic attractor was plotted by choosing an initial point
in the gray region and plotting trajectory points 1001, 1002,...,1,000,000.
Experience has shown that almost any other point chosen from the gray would
have yielded the same picture. Of course, we can subvert the process by choosing
a nonattracting fixed point for the initial point, on or off the attractor. Then the
plot would only show a single point, assuming that small computer roundoff errors
did not push us away.
6.2 CHAOTIC ATTRACTORS
A fixed-point sink is easily seen to satisfy the definition of attractor, since it
attracts an entire
⑀
-neighborhood. (The forward limit set of each point in the
neighborhood is the sink.) Periodic sinks are also attractors.
238

6.2 CHAOTIC ATTRACTORS
14
⫺2
⫺88
(a)
4
⫺2
⫺
(b)
Figure 6.4 More chaotic attractors of plane maps.
The attractors are shown in black inside their basins, which are shown in gray.
(a) A chaotic attractor of the H
´
enon map (6.1) with a ⫽ 2.1, b ⫽⫺0.3. The basin
boundary, as well as the attractor, is fractal. White points are attracted to infinity.
(b) The chaotic attractor of the time–2
map of the forced damped pendulum. The
basin of this attractor, shown in gray, consists of virtually all initial conditions.
The unit interval is the forward limit set of a chaotic orbit of the logistic
map G ⫽ g
4
and it attracts an interval of initial conditions (itself), so it is a
chaotic attractor. Similarly, the unit interval is a chaotic attractor for the tent
map T
2
(x).
E XAMPLE 6.4
Let f(x) ⫽ 2x (mod 1). As in Exercise 3 of Chapter 4, we can associate
with each point in [0, 1] an itinerary (an infinite sequence of 0’s and 1’s) on
which the shift map represents the action of f. All points in the subinterval
[(k ⫺ 1)2
⫺n
,k2
⫺n
], 1 ⱕ k ⱕ 2
n
, are represented by a finite sequence of n symbols.
By constructing a symbol sequence that contains every possible finite sequence,
a point with an orbit that is dense in [0, 1] can be shown to exist.
✎ E XERCISE T6.4
Show that [0, 1] is a chaotic attractor for the 2x (mod 1) map of Example
6.4.
239

C HAOTIC ATTRACTORS
W HAT IS AN ATTRACTOR?
T
he term attractor is used for the forward-time limit of an orbit
that attracts a significant portion of initial conditions. A sink is an
example, since it attracts at least a small neighborhood of initial
values.
An attractor should be irreducible in the sense that it includes only
what is necessary. The set consisting of the sink together with one
of the orbits approaching the sink is also a set that attracts initial
conditions, but for the reason that it contains the sink. Only the sink
is actually needed. Irreducibility is guaranteed by requiring that the
attractor contain a dense orbit, an orbit that comes arbitrarily close
to each point in the attractor.
Besides irreducibility, the attractor must have the property that a
point chosen at random should have a greater-than-zero probability
of converging to the set. A saddle fixed point is irreducible in the
above sense and does attract orbits: for example, the one whose initial
condition is the fixed point itself. However, this initial condition is
very special; the definition requires that an attractor must attract a
set of initial values of nonzero state space volume.
Chaos introduces a new twist. Chaotic orbits can be attracting, as
shown in this chapter. If the forward limit set of such a chaotic orbit
contains the orbit itself (and therefore contains a dense orbit), then
the attractor is a chaotic attractor.
E XAMPLE 6.5
The map of Example 6.4, although not continuous as a map of the interval,
is continuous when viewed as the map f(
) ⫽ 2
of the circle. Using polar
coordinates, we can embed f into a map of the plane
f(r,
) ⫽ (r
1 2
, 2
).
See Figure 6.5. There is a repelling fixed point at the origin, which is the forward
limit set
(0). The circle r ⫽ 1 is also the forward limit set of an orbit with
Lyapunov exponent ln 2, which we can conclude from Example 6.4. This means
240

6.2 CHAOTIC ATTRACTORS
x
y
Figure 6.5 Map for which the unit circle is a chaotic attractor.
Two orbits are shown for the map f(r,
) ⫽ (r
1 2
, 2
) given in polar coordinates.
All orbits except the origin converge to the unit circle r ⫽ 1, which has a dense
chaotic orbit.
the circle is a chaotic set. All points other than the origin are attracted to this
circle, making the circle a chaotic attractor.
E XAMPLE 6.6
The piecewise linear map on the unit interval illustrated in Figure 6.6 is
called the W-map. If we restrict our attention to the subinterval S ⫽ [1 4, 3 4],
0 1/2
1
1/2
1
A
1
A
2
A
3
A
4
Figure 6.6 The W-map of the unit interval.
The set [1 4, 3 4] is a chaotic attractor.
241
C HAOTIC ATTRACTORS
the map operates like the tent map. Points from the remainder of the unit interval
are immediately mapped into S. Because of the analogy with the tent map, we
know that S contains a dense orbit with Lyapunov exponent ln 2. That makes S a
chaotic set. Further, the entire unit interval is attracted to S, making S a chaotic
attractor.
E XAMPLE 6.7
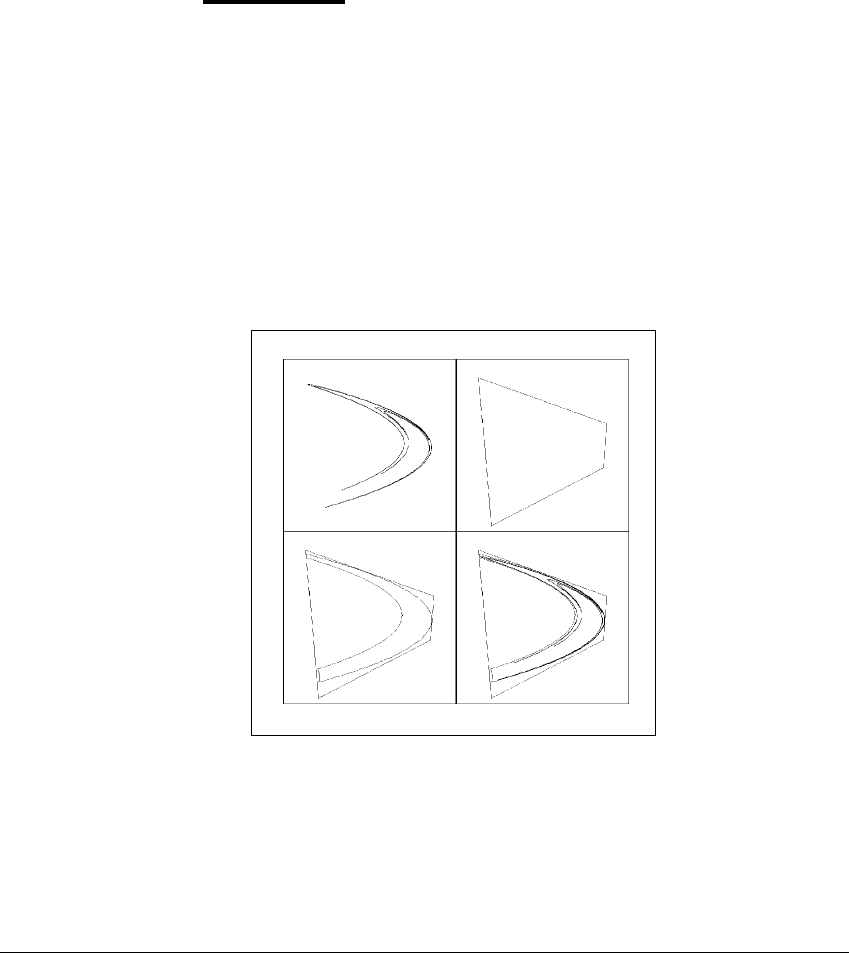
H
´
enon observed the attractor shown in Figure 6.7 for the map (6.1) with
a ⫽ 1.4andb ⫽ 0.3. In addition, he found a quadrilateral in the plane, shown
in Figure 6.7(b), which maps into itself when the function is applied to it once.
A bounded neighborhood that the map sends into itself, such as the quadri-
lateral, is called a trapping region. A quadrilateral trapping region, together with
its forward image, is shown in Figure 6.7(c). The Jacobian determinant of H is
J ⫽⫺0.3 (minus the coefficient of y) at all points in the plane. Thus the image
under H of a region of the plane is decreased by the factor |J| ⫽ 0. 3. Because H
Figure 6.7 The H
´
enon attractor and a trapping region.
The attractor of the map f(x, y) ⫽ (1.4 ⫺ x
2
⫹ 0.3y, x)shownin(a)iscontained
in a quadrilateral trapping region shown in (b). The trapping region maps into itself
and contracts in area by the factor 0.3. The quadrilateral and its image under f are
shown in (c). Since f is area-contracting, forward iterates of the trapping region
shrink down to a limit set (the attractor) that has zero area. The figures in (a) and
(c) are superimposed in (d).
242

6.2 CHAOTIC ATTRACTORS
is area-contracting, forward iterates of the quadrilateral shrink to zero area in the
limit.
What are the implications of a trapping region for an area-contracting map
such as the H
´
enon map? One iterate maps the region inside itself to the shape in
Figure 6.7(c), which is 30% of the original size. Two iterates map the quadrilateral
to 9% of its original size, to a shape folded further within itself. The limit of this
process is the chaotic attractor shown in Figure 6.7(d). Numerical approximation
of the Lyapunov exponents on the attractor yield .39 and ⫺1.59, so that this is
a chaotic attractor—assuming that it is not just a long periodic orbit. That fact
is surprisingly hard to prove and as of this writing, it has not been established for
these parameter values of the map. It is likely that there is a chaotic attractor
here but it may never be proved. One difficulty is that arbitrarily small changes
in the parameters (0.3 and 1.4) can be made so that the system has an attracting
periodic orbit.
E XAMPLE 6.8
The circle r ⫽ 1 in Example 6.5 is a good prototype of a chaotic attractor.
It is properly contained in a basin of attraction (unlike the logistic map g
4
), and
the map is smooth, at least around the attractor (unlike the W-map). It is not,
however, an invertible map. By increasing the dimension of the underlying space,
we can define a similar example, called the solenoid, in which the map is one-to-
one. The underlying set of this chaotic attractor was described first by topologists
(see, for example, (Hocking and Young, 1961)) and then as a dynamical system
by (Smale, 1967).
We define the map f on the solid torus (a subset of ⺢
3
), which we think of
as a circle of two-dimensional disks. The disk D in ⺢
2
can be defined with one
complex coordinate z, as D ⫽ 兵z : |z| ⱕ 1其. Then points in the solid torus T can
be described by two coordinates:
T ⫽ 兵(t, z):t 僆 [0, 1) and |z| ⱕ 1,z僆 ⺓其.
The map f : T → T is defined as follows:
f(t, z) ⫽
2t (mod 1),
1
4
z ⫹
1
2
e
2
it
,
where e
ix
⫽ cos x ⫹ i sin x.
In order to understand this map geometrically, we refer to the picture of T
and f(T) in Figure 6.8(a). Think of the solid torus T as being stretched to a longer,
thinner loop. Then it is twisted, doubled over, and placed back into T. The image
243
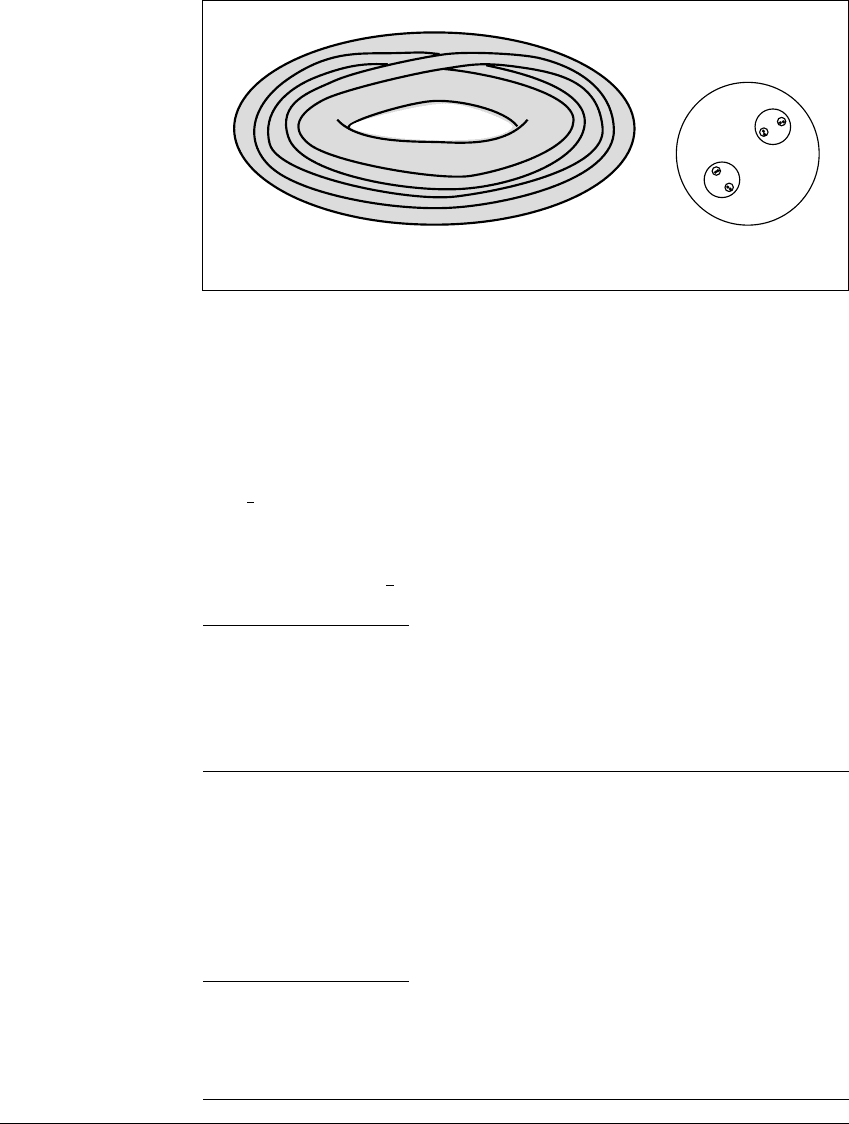
C HAOTIC ATTRACTORS
(a) (b)
Figure 6.8 Schematic picture of the solenoid map.
(a) The solid torus T together with the image f(T) is shown. (b) A cross-sectional
disk D
t
in the solid torus T is shown together with the intersection of f(T), f
2
(T),
and f
3
(T)withD
t
.
of T now intersects each cross-sectional disk D
t
in two smaller disks, D
0
and D
1
,
each
1
4
the diameter of the original. The second iterate f
2
(T ) intersects each D
t
in
four smaller disks, etc. Figure 6.8(b) shows a cross-sectional disk D
t
of T together
with intersections of f(T), f
2
(T ), and f
3
(T )withD
t
. Any two points in T whose
t-coordinates differ by
1
2
map to the same cross-sectional disk.
✎ E XERCISE T6.5
(a) Identify the pre-images of D
0
and D
1
, the intersection of f(T)withthe
cross-sectional disk D
t
. (b) Show that D
0
and D
1
are symmetric with respect
to the origin in D
t
.
The map f is uniformly stretching in the t direction: Each orbit has a positive
Lyapunov exponent of ln 2. The attractor A ⫽
nⱖ0
f
n
(T ) intersects each D
t
in a
Cantor set, and A has zero volume inside T, the basin of attraction. The solenoid
has many interesting topological and dynamical properties that we do not pursue
here. For a detailed discussion, see (Robinson, 1995).
We leave the task of identifying a dense orbit for A to the following exercise.
✎ E XERCISE T6.6
Find a way to assign bi-infinite symbol sequences to points in A, as done
earlier for the horseshoe map. Determine an orbit that is dense in A.
244

6.3 CHAOTIC ATTRACTORS OF E XPANDING I NTERVAL M APS
6.3 CHAOTIC ATTRACTORS OF EXPANDING
INTERVAL MAPS
In this section, we take a closer look at a class of maps of the unit interval that
have chaotic attractors. Let p
0
⬍ p
1
⬍⭈⭈⭈⬍ p
k
be points on the real line and let
I be the interval [p
0
,p
k
]. Define the closed intervals A
i
⫽ [p
i⫺1
,p
i
]. Let f : I → I be
a map whose derivative satisfies |f
(x)| ⱖ
␣
⬎ 1 except possibly at the p
i
(where
f may have a corner, or in some other way not be differentiable). We will call
such a map a piecewise expanding map with stretching factor
␣
. We say that
兵p
0
,p
1
,...,p
k
其 is a stretching partition for the piecewise expanding map f if, for
each i, f(A
i
) is exactly the union of some of the intervals A
1
,...,A
k
. A stretching
partition satisfies the covering rule of Chapter 3, which allows the construction
of transition graphs for the partition intervals A
i
. (It is also the one-dimensional
analogue of the concept of “Markov partition,” defined in Chapter 5.) An example
of a piecewise expanding map is the W-map of Figure 6.6.
We found in Chapter 3 that when there is a partition that satifies the
covering rule, symbol sequences can be used to keep track of the itinerary of an
orbit of f. For example, if the orbit begins in interval A
1
, then maps into A
2
,and
then to A
3
, its itinerary would begin: .A
1
A
2
A
3
.... Of course, there is a countable
set of orbits that eventually land precisely on one of the points p
i
.Weignorethese
special orbits in this discussion and concentrate on the remaining uncountably
many orbits.
Not all sequences of the symbols A
1
,...,A
k
may be achievable by orbits of f.
For example, let f be the W-map as shown in Figure 6.6. Any orbit that begins
in subinterval A
1
⫽ [0, 1 4] maps to the subinterval [1 4, 3 4] ⫽ A
2
傼 A
3
; but
f(A
2
) ⫽ f(A
3
) ⫽ A
2
傼 A
3
, meaning that the orbit will never return to A
1
.That
is, .A
1
A
2
...is an allowable symbol sequence for f, but .A
2
A
1
...is not. In general,
if B and C are two subintervals for a stretching partition, C is allowed to follow B
in the symbol sequence of a point of the interval I if and only if f(B) ⫽ C 傼 (other
subintervals).
The fact that a continuous map f is stretching by at least the factor
␣
⬎ 1
causes the dynamics of f to be well organized. Let L be the length of the entire
interval I. For an allowable sequence .B
1
...B
n
of n symbols (repetitions allowed),
there is a subinterval of length at most
L
␣
n⫺1
, which we call an order n subinterval,
whose points follow that itinerary. For each n, the order n subintervals virtually fill
up I: every point of I either lies in some order n subinterval or is on the boundary
of an order n subinterval. An infinite allowable sequence represents one point in
I,sinceL
␣
n⫺1
→ 0asn →
⬁
.
245
