Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

C HAOTIC ATTRACTORS

The derivative (f

)



) ⫽ f



n⫺1

) ⭈⭈⭈f



) is greater than

␣

for each x

|(f

)



1 n

ⱖ

␣

. (6.3)

The Lyapunov number for the orbit starting at x

is therefore at least

␣

,ifthe

limit exists. Although our formal deﬁnition of chaotic orbit in Chapter 3 requires

the Lyapunov number to be greater than 1, we will relax the requirement that

the limit of (6.3) exists for the statement of Theorem 6.11. For readers with an

advanced calculus background, we point out that whether the limit exists or not,

lim inf |(f

)



1 n

ⱖ

␣

⬎ 1, (6.4)

which is a more inclusive deﬁnition of chaos.

E XAMPLE 6.9

Let f be the tent map on the unit interval [0, 1]. We studied the itineraries

of this map in Chapter 3 as an example of chaotic orbits. It is clear that 兵0,

, 1其

is a stretching partition for the tent map, with

␣

⫽ 2.

E XAMPLE 6.10

Let f be the W-map of Figure 6.6. The stretching partition is 0 ⬍

⬍

⬍ 1, and

␣

⫽ 2. Allowable symbol sequences are arbitrary sequences of

, A

with the restriction that every symbol must be followed by either A

or A

.ThusA

and A

can appear only as the leftmost symbol. This corresponds

to the fact that the intervals [0, 1 4] and [3 4, 1] map into the interval [1 4, 3 4]

and the points never return. The transition graph for this partition is shown in

Figure 6.9.

The facts we have developed in this section are summarized in the following

theorem. The proof of the last property is left to the reader.

Theorem 6.11 Let f be a continuous piecewise expanding map on an interval

I of length L with stretching factor

␣

,andletp

⬍ ⭈⭈⭈ ⬍ p

be a stretching partition

for f.

1. Each allowable ﬁnite symbol sequence .A

⭈⭈⭈A

corresponds to a subinterval

of length at most

␣

n⫺1

2. Each allowable inﬁnite symbol sequence .A

⭈⭈⭈corresponds to a single

point x of I such that f

(x) 僆 A

i⫹1

for i ⱖ 0, and if the symbol sequence is

not periodic or eventually periodic, then x generates a chaotic orbit.

246

6.3 CHAOTIC ATTRACTORS OF E XPANDING I NTERVAL M APS

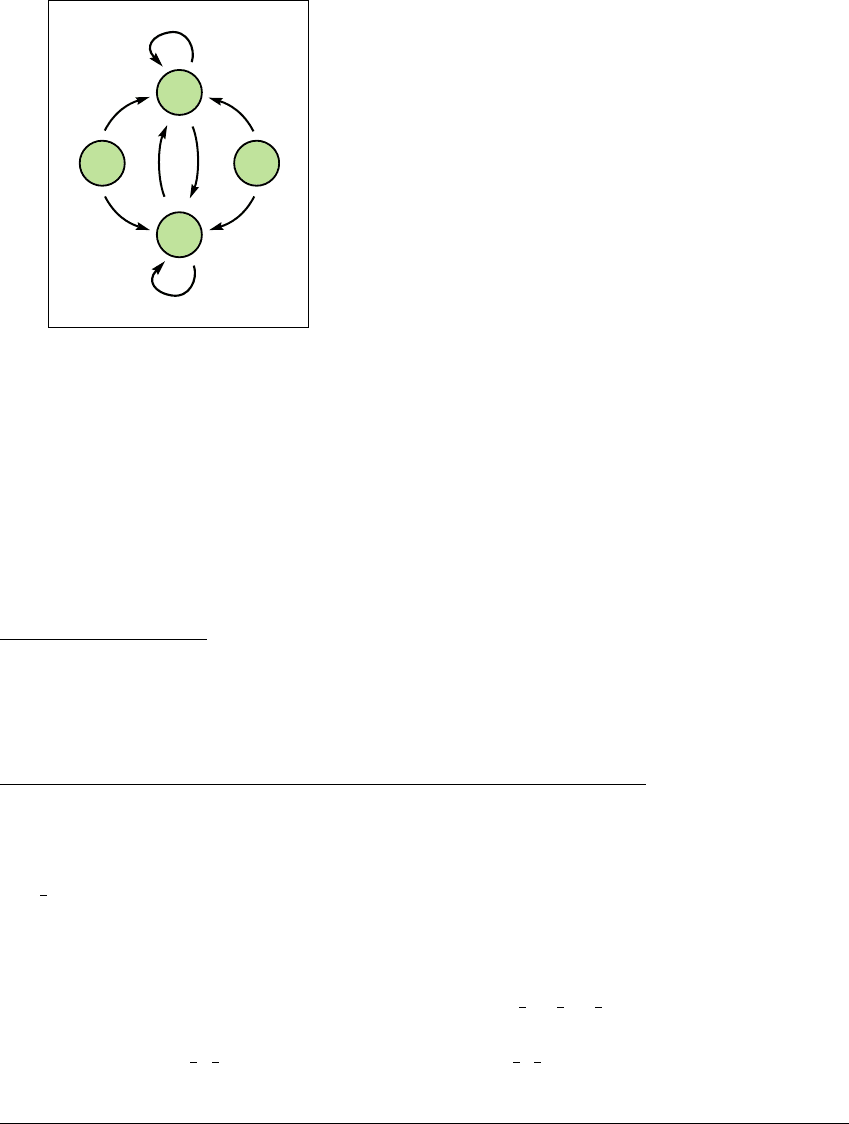
Figure 6.9 Transition graph for the W-map.

The unit interval is partitioned into four subsets, A

, A

,andA

, on each of

which the map is stretching. The

␻

-limit set of any orbit is A

傼 A

3. If, in addition, each pair of symbols B and C (possibly B ⫽ C) can be

connected by allowable ﬁnite symbol sequences B ⭈⭈⭈C and C ⭈⭈⭈B,thenf

has a dense chaotic orbit on I, and I is a chaotic attractor.

✎ E XERCISE T6.7

Assuming the hypothesis of Theorem 6.11 and, in addition, that each pair

of symbols can be connected by an allowable symbol sequence, show that

f has a chaotic orbit that is dense in I.

Theorem 6.11 is extremely useful for proving the existence of chaotic

attractors on the real line. Consider the tent map, with stretching partition

0 ⬍

⬍ 1 and symbols A

and A

corresponding to the two subintervals. Since

f(A

) ⫽ A

傼 A

and f(A

) ⫽ A

傼 A

, the pair of symbols A

and A

can occur

in either order, and part 3 of Theorem 6.11 applies. The unit interval is a chaotic

attractor for the tent map.

The W-map of Example 6.10 has a stretching partition 0 ⬍

⬍

⬍ 1.

Because A

cannot occur, part 3 of Theorem 6.11 does not apply. However, if

we restrict the map to [

], part 3 again applies to show that [

] is a chaotic

attractor. In fact this attractor is essentially the tent map attractor.

247

C HAOTIC ATTRACTORS

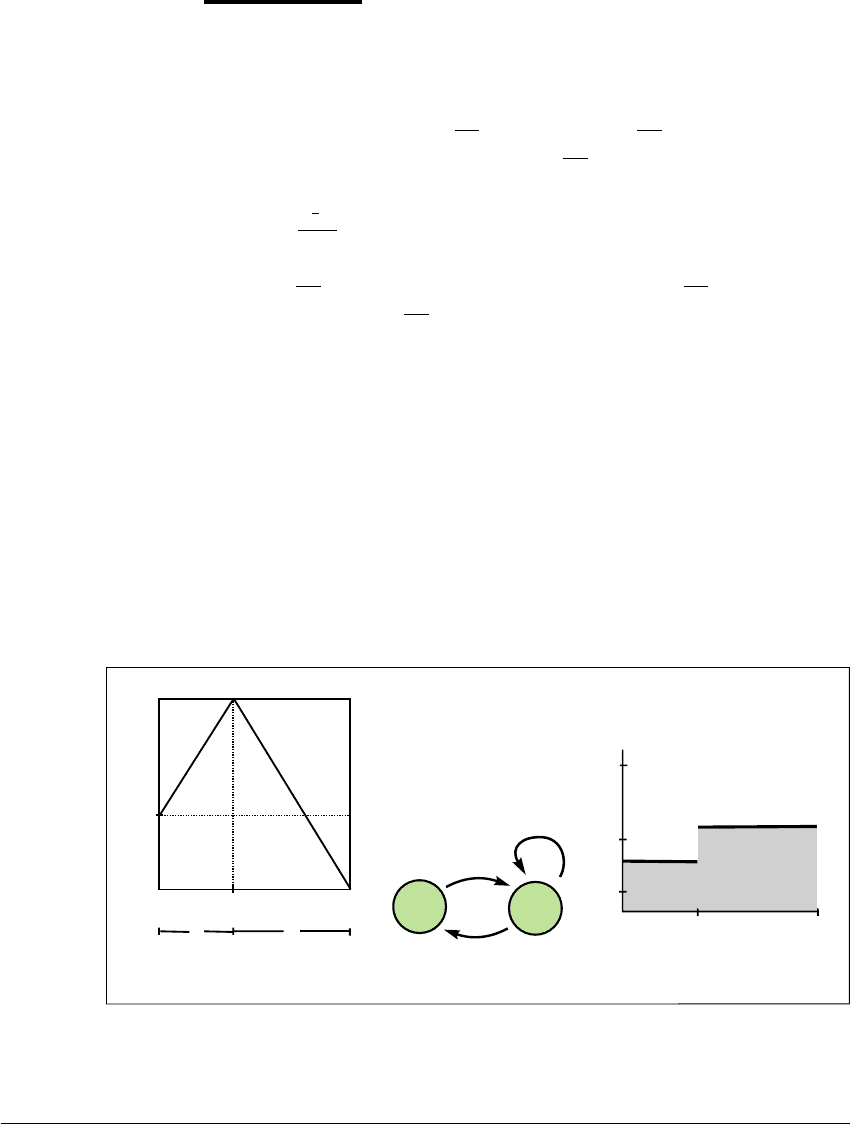
E XAMPLE 6.12

(Critical point is period three.) Deﬁne

f(x) ⫽



a⫹1

⫹ ax if 0 ⱕ x ⱕ

a⫹1

a ⫺ ax if

a⫹1

ⱕ x ⱕ 1

where a ⫽



5⫹1

is the golden mean. The map is sketched in Figure 6.10. Note

that a is a root of the equation a

⫽ a ⫹ 1. Because of the careful choice of a,

we have f(

a⫹1

) ⫽ 1, and since also f(1) ⫽ 0andf(0) ⫽

a⫹1

, the peak of the

function f occurs at c ⫽

a⫹1

⬇ 0.382, which is a period-three point for f.

The partition 0 ⬍ c ⬍ 1 is a stretching partition for f. Deﬁne the subinter-

vals A ⫽ [0,c]andB ⫽ [c, 1]. Notice that f(A) ⫽ B and f(B) ⫽ A 傼 B. Allowable

symbol sequences for orbits of f consist of strings of A and B such that A cannot

be followed by A. The stretching factor under f is the golden mean, which is

approximately 1.618.

Can part 3 of Theorem 6.11 be applied? Symbol sequences AB, BA,andBB

can obviously occur, and since ABA is also permitted, all possible pairs can be

connected. Therefore [0, 1] is a chaotic attractor for the map f.

A B

(a) (b) (c)

Figure 6.10 Map for which the critical point is period three.

(a) Sketch of map. (b) Transition graph. (c) Invariant measure for (a); see Section

6.4.

248

6.4 MEASURE

In our quest to identify and describe ﬁxed-point, periodic, and chaotic attractors,

we have considered them as sets of points. Although this does a good job of

characterizing the attractor when the point set is ﬁnite, the case of chaotic

attractors presents an extra challenge, since they must contain inﬁnitely many

points.

When studying chaotic attractors we must give up on the idea of keeping

track of individual points, and instead do our bookkeeping over regions. The

term “measure”, to which this section is devoted, refers to a way of specifying how

much of the attractor is in each conceivable region.

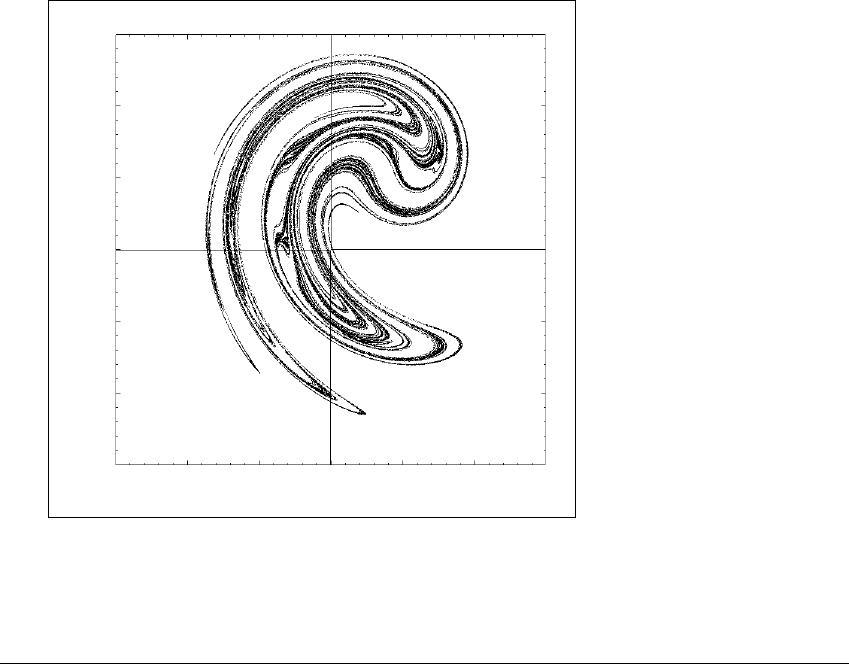
For example, imagine a box drawn in the plane that contains part of the

Ikeda attractor, such as box 1 in Figure 6.11. How could we measure the proportion

of points on the attractor that are contained in the box? We will use the “rain

⫺2

⫺12

Figure 6.11 100,000 points on the Ikeda attractor.

The proportion landing in each of the 4 boxes is an approximation to the natural

measure of the Ikeda attractor for that box. Boxes 1, 2, 3, and 4 contain about 30%,

36%, 17%, and 17%, respectively.

249

C HAOTIC ATTRACTORS

gauge” technique and measure the proportion of points that fall into box 1 from

a typical orbit.

Choose an initial point at random to start an orbit. At each iteration, we

record whether the new orbit point fell into the box or not. We keep this up for a

long time, and when we stop we divide the number that landed in the box by the

total number of iterates. The result would be a number between 0 and 1 that we

could call the “Ikeda measure” of the box. In Figure 6.11, 29,798 of the 100,000

points shown lie in box 1, so that approximately 30% of the points fall into the

box.

This number could be regarded as the probability that a point of the Ikeda

attractor lies in the box. A box located away from the attractor would have Ikeda

measure zero. In fact, on the basis of the 100,000 points shown, the Ikeda measure

of box 1 is 0.29798. The measures of boxes 2, 3, and 4 are 0.35857, 0.17342,

and 0.17003, respectively. These four numbers add up to 1 because each of the

100,000 points landed in one of the four boxes.

Now we will make our ideas on measure a little more precise. The two most

important properties of the rain-gauge method are nonnegativity and additivity,

namely:

(a) The measure of any set is a nonnegative number, and

(b) The measure of a disjoint union of a ﬁnite or countably inﬁnite number

of sets is equal to the sum of the measures of the individual sets.

If A is a subset of B, we will denote by B ⶿ A the complement of A in B,thesetof

points in B that do not belong to A. It follows from (b) that if A is a subset of B,

then the measure of the complement B ⶿ A is the difference of the measures of B

and A.

A method of assigning a number to each closed set so that (a) and (b) are

satisﬁed is called a measure. (See Section 8.2 for an introduction to closed sets.)

The ordinary measures we are used to, such as length on ⺢

,areaon⺢

,and

volume on ⺢

are called Lebesgue measures when extended to apply to all closed

sets. Although fact (b) is true when the union is a countably inﬁnite union, we

can’t expect (b) to hold for uncountable disjoint unions. The length of a single

point is zero, and an uncountable union of them makes a unit interval with length

one.

Once a measure is deﬁned for all closed sets, we can extend the deﬁnition

to many other sets with the help of properties (a) and (b). For example, using

Lebesgue measure (length) m on the real line gives the length of the unit interval

to be one, m([0, 1]) ⫽ 1. Since we know that the length of the single point set

250

6.4 MEASURE

兵0其 is zero, we can ﬁnd the measure of the half-open interval (0, 1]. Rule (b) gives

m(兵0其) ⫹ m((0, 1]) ⫽ m ([0, 1]), so that we ﬁnd m((0, 1]) ⫽ 1. In this way we can

deﬁne the measure of many nonclosed sets. A Borel set is a set whose measure

can be determined by the knowledge of the measure of closed sets and a chain

of applications of rules (a) and (b). The set (0, 1) is a Borel set because rule (b)

allows deﬁnition of its measure from other sets: m((0, 1)) ⫹ m(兵1其) ⫽ m((0, 1]),

from which we conclude that m((0, 1)) ⫽ 1 ⫺ 0 ⫽ 1. To summarize, the Borel

sets are those that have a well-deﬁned number assigned to them by the measure.

It is hard to conceive of a set of real numbers that is not a Borel set, but

they do exist. See any book on measure theory for examples. Strictly speaking,

our deﬁnition of measure, with its scope limited to closed sets and those that can

be formed from them using (b), is often called a Borel measure. Less restrictive

deﬁnitions of measure exist but will not be considered in this book.

✎ E XERCISE T6.8

Show that if

␮

is a measure, A and B are Borel sets,

␮

(B) ⫽ 0, and A 傺 B,

then

␮

(A) ⫽ 0.

The rain-gauge method of generating a measure has two further properties

that are important. First, since it measures the proportion of points falling into a

set, it satisﬁes the following property:

A measure that satisﬁes rule (c) is called a probability measure.

Finally, notice that the amount of rain-gauge measure in a box using points

generated by the map f is the same as the measure of the pre-image of the box

under the map f. The reason is that all of the pre-iterates of B willendupinB on

their next iteration. A measure

␮

that satisﬁes the property

(d)

␮

⫺1

(S)) ⫽

␮

(S) for each closed set S

is called an f-invariant measure. Ikeda measure satisﬁes both (c) and (d), so it is

an f-invariant probability measure.

Lebesgue measure is generated by the rain-gauge technique by replacing

the Ikeda attractor with a random number generator. Assume that we have a

251

C HAOTIC ATTRACTORS

method for producing pairs (x, y) of real numbers that randomly ﬁll the square

[0, 1] ⫻ [0, 1] in a uniform way. In theory, if the random number generator is truly

random and uniform, we could use this device to ﬁnd area: We could call it “area

measure”, by analogy with Ikeda measure. A box with dimensions a ⫻ b lying in

the square [0, 1] ⫻ [0, 1] will get a proportion of randomly generated points that

converges to ab with time.

A random number generator on a computer is pseudo-random, meaning

that it is a deterministic algorithm designed to imitate a random process as closely

as possible. If the random number program is run twice with the same starting

conditions, it will of course yield the same sequence of random numbers, barring

machine failure. That is the meaning of “deterministic”. This is sometimes useful,

as when a simulation needs to be repeated a second time with the same random

inputs. However, it is important to be able to produce a completely different

random sequence. For this reason most random number generators allow the user

to set the seed, or initial condition, of the program. If the algorithm is well-

designed, it will measure the area of an a ⫻ b rectangle to be ab, no matter which

seed is used to start the program.

The relationship of an invariant measure to a chaotic attractor is the same

as the relationship of standard area to a uniform random number generator. The

important concept is that the percentages of points in a given rectangle in Ikeda

measure are independent of the initial value of the orbit used in the rain-gauge

technique. If this is true, then Ikeda measure of a rectangle has a well-deﬁned

meaning. In the same way, we know that an a ⫻ b rectangle in the plane has area

ab, even though there may be no uniform random number generator nearby to

check with.

Both chaotic attractors and random number generators could fail to give the

correct measure. For all we know, our random number generator might produce

the inﬁnite sequence of points (1 2, 1 2), (1 2, 1 2),....In fact, this sequence

of numbers is as likely to occur as any other sequence. Obviously this output

of random numbers will not correctly measure sets. It would imply that the set

[0, 1 4] ⫻ [0, 1 4] has measure zero. The corresponding problem with an attractor

occurs, for example, if the initial value used to generate the points happens to be a

ﬁxed point. The orbit generated will not generate Ikeda measure; it will generate

a measure that is 1 if the box contains the ﬁxed point, and 0 if not.

To have a good measure, we need to require that almost every initial value

produces an orbit that in the limit measures every set identically. That is, if we

ignore a set of initial values that is a measure zero set, then the limit of the

proportion of points that fall into each set is independent of initial value. A

measure with this property will be called a natural measure.

252

6.5 NAT U R A L M EASURE

6.5 NATURAL MEASURE

Now we are ready to make the rain-gauge measure into a formal deﬁnition. We

need to introduce some ﬁne print to the deﬁnition of rain-gauge measure that is

important for borderline cases. First, deﬁne the fraction of iterates of the orbit

兵 f

)其 lying in a set S by

F(x

,S) ⫽ lim

n→

⬁

#兵 f

)inS :1ⱕ i ⱕ n其

. (6.5)

E XAMPLE 6.13

Let f(x) ⫽ x 2. All orbits are attracted to the sink x ⫽ 0. First deﬁne

⫽ [⫺1, 1]. For any initial point x

, the fraction F(x

) ⫽ 1. Even if the orbit

doesn’t start out inside S

, it eventually moves inside S

and never leaves. The

ratio in the deﬁnition (6.5) tends to one in the limit as n →

⬁

.IfwedeﬁneS

to be a closed interval that does not contain 0, then the orbit would eventally

leave the interval and never return, so that F(x

) ⫽ 0 for any x

. For these sets

and S

, the rain-gauge technique gives the correct answer, since the measure

should be concentrated at x ⫽ 0.

Now let S

⫽ [0,

⬁

) and compute the fraction F(x

) for various x

.If

⬍ 0, no iterates of the orbit lie in S

,andF(x

) ⫽ 0. If x

ⱖ 0, then all

iterates of the orbit lie in S

,andF(x

) ⫽ 1.

Because one of the boundaries of S

lies at the sink, this is a borderline

case. The rain-gauge technique is too unreﬁned to work here. When we ask what

proportion of a typical orbit lies in S

, we get conﬂicting answers, depending on

. A similar problem occurs for an orbit starting in the basin of, say, a chaotic

enon attractor S.Ifv

is attracted to S but not in S,thenf

) gets very close

to S, but is never in S. Hence the fraction F(v

,S) ⫽ 0. On the other hand, if

we fatten the attractor by a tiny amount, the problem is ﬁxed. In other words, if

r ⬎ 0, then F(v

,N(r, S)) ⫽ 1, where we have used the notation

N(r, S) ⫽ 兵x : dist(x, S) ⱕ r其, (6.6)

to denote the set of points within r of the set S.

The difﬁculty in assigning the correct value to the fraction of the orbit that

lands inside a given set is solved by the following deﬁnition of natural measure.

Assume that f is a map and that S is a closed set.

253

C HAOTIC ATTRACTORS

Deﬁnition 6.14 The natural measure generated by the map f,also

called f-measure,isdeﬁnedby

␮

(S) ⫽ lim

r→0

F(x

,N(r, S)) (6.7)

for a given closed set S, as long as all x

except for a measure zero set give the

same answer.

Quite often we will want to apply this deﬁnition to f limited to a subset of its

domain. It is common for this subset to be a basin of attraction. For example, the

logistic map G(x) ⫽ 4x(1 ⫺ x) on the unit interval [0, 1] has a natural measure

which is investigated in detail in Challenge 6. Notice that even in this case, we

must allow for a measure zero set of x

which do not go along with the crowd. Not

every orbit 兵 f

)其 can be used to evaluate

␮

(S). For example, we know that G

has two ﬁxed-point sources in [0, 1]. Neither of these orbits can be used; nor can

any of the periodic orbits of G. Together they make up a countable set, which has

measure zero. On the other hand, the map G on the entire real line does not have

a natural measure, since initial values outside of [0, 1] are attracted to

⬁

,andso

the condition that the exceptions be a measure zero set is not satisﬁed.

✎ E XERCISE T6.9

Show that properties (a), (b), (c), and (d) in the deﬁnition of invariant

measure hold for a natural measure.

With this more sophisticated version of natural measure, the difﬁculty of

determining the fraction of an orbit lying within a set disappears. For f(x) ⫽ x 2

and S ⫽ [0,

⬁

), the set N(r, S) ⫽ [⫺r,

⬁

), and F(x

,N(r, S)) ⫽ 1 for any x

,as

long as r ⬎ 0. Therefore

␮

(S) is the limit as r → 0, which is 1. (The fact that

F(x

,N(0,S)) ⫽ 0ifx

⬍ 0 is now irrelevant.)

Any interval [a, b]witha ⬍ 0 ⬍ b will have f-measure equal to 1. Even if

some of the original iterates miss the interval, eventually they will stay within a

neighborhood of 0 so small that it is contained entirely within [a, b]. The limiting

ratio of orbit points in the interval to the total approaches 1 in the limit.

Now consider an interval with one endpoint equal to 0. This is another

borderline case. An orbit converging to 0 eventually moves into the set N(r, S)

for any r ⬎ 0. Therefore

␮

([a, 0]) ⫽

␮

([0,b]) ⫽ 1.

A singleton set 兵x其 has f-measure zero if x ⫽ 0 because it is contained in an

interval with f-measure zero, by Exercise T6.8. On the other hand,

␮

(兵0其) ⫽ 1.

The measure of other sets can be found using the above facts in conjunction with

Property (b). For example,

␮

((0, 1]) ⫽

␮

([0, 1]) ⫺

␮

(兵0其) ⫽ 1 ⫺ 1 ⫽ 0.

254

6.5 NAT U R A L M EASURE

W HY M EASURE?

hy do we study measure in connection with chaotic attractors? At

the very least, we must know that the natural measure of a map is not

atomic if there is a chaotic attractor. More importantly, the existence

of a natural measure allows us to calculate quantities that are sampled

and averaged over the basin of attraction and have these quantities

be well-deﬁned. Perhaps the most important such quantity for the

purposes of this book is the Lyapunov exponent. For an orbit of a

one-dimensional map f, the Lyapunov exponent is ln |f



| averaged

over the entire orbit. In order to know that the average really tells us

something about the attractor (in this case, that orbits on the attractor

separate exponentially), we must know that we will obtain the same

average no matter which orbit we choose. We must be guaranteed

that an orbit chosen at random spends the same portion of its iterates

in a given region as any other such orbit would. That is precisely what

a natural measure guarantees.

Recent progress has been made in the mathematical veriﬁcation of the

existence of chaotic attractors for the H

enon family f

a,b

. (Benedicks

and Carleson, 1991) have shown that for small negative Jacobian

(small ﬁxed b), there is a set of parameter a values with positive

Lebesgue measure such that the attracting set for f

a,b

is a chaotic

attractor. Interestingly, the particular a values with chaotic attractors

cannot be speciﬁed. Also, (Benedicks and Young, 1996) have shown

that there is a natural measure associated with these attractors. See

(Palis and Takens, 1993) for more details.

A measure is atomic if all of the measure is contained in a ﬁnite or countably

inﬁnite set of points. To summarize our conclusions for Example 6.13, the natural

measure for f is the atomic measure located at the sink x ⫽ 0. In general, a map

for which almost every orbit is attracted to a ﬁxed-point sink will, by the same

reasoning, have an atomic natural measure located at the sink.

Ikeda measure is an example of a measure generated by a map. A different

measure would be generated by a chaotic H

enon attractor as in Figure 6.1(a) or

6.4(a). Other map-generated measures are extremely simple and look nothing

like a random number generator.

255