Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях

Подождите немного. Документ загружается.

а второго типа

, .

Если определить

то получим

В этом случае проекции

независимы по первому типу, но уже зависимы по

второму.

-функции условных проекций второго типа равны

, .

Пример 1.8.

Пусть в

определено

-отношение:

где

такие, что .

Из уравнения имеем

откуда .

Подставляя полученное выражение в , получим

По аналогии, для

имеем

где .

Для условных проекций второго типа по (1.13) и (1.14) получаем выражения:

Таким образом, если

, то

независимы по второму типу, поскольку в этом случае

и, кроме того, имеем

, .

При

множества

являются зависимы по второму типу.

Если положить, например,

= с

, то

и, следовательно,

т.е. проекции

являются независимыми по первому типу. Аналогичное утверждение

справедливо при

= с

Теорема 1.1.

Пусть и существуют такие и , что

Тогда, если , то

являются проекциями

-отношения

оказательство

Покажем, например, что

B = Q

. Для произвольного фиксированного

имеем:

Равенство

A = Q

доказывается аналогично.

Теорема 1.2.

Пусть и существуют такие и , что

Тогда, если

нормальные

-множества, т.е.

то они являются проекциями

-отношения

оказательство.

Покажем, например, что

B = Q

. Действительно, для произвольного фиксированного

имеем:

Равенство

A = Q

доказывается аналогично.

Замечание

. Из (1.17) и (1.18) выводятся следующие соотношения

аналогичные формулам Байеса в теории вероятности.

Если по аргументам

-функции ясно, на каком базовом множестве она задана и понятен ее

смысл, то можно применять более простую форму записи, опуская обозначения

-множеств у

соответствующих

-функций (например, ).

1.7. Отображение F-множеств

В ТНМ считается, что произвольное

-отношение в

∗

устанавливает определенное

отображение межд

. П

сть в

∗

задано некоторое

-отношение с ф

нкцией

принадлежности , которое можно толковать как нечеткий график

-отображения,

вводимого следующим образом.

Говорят, что задано

-отображение

f: X

→

, если каждому

A F(X)

ставится в соответствие

(A) F(Y)

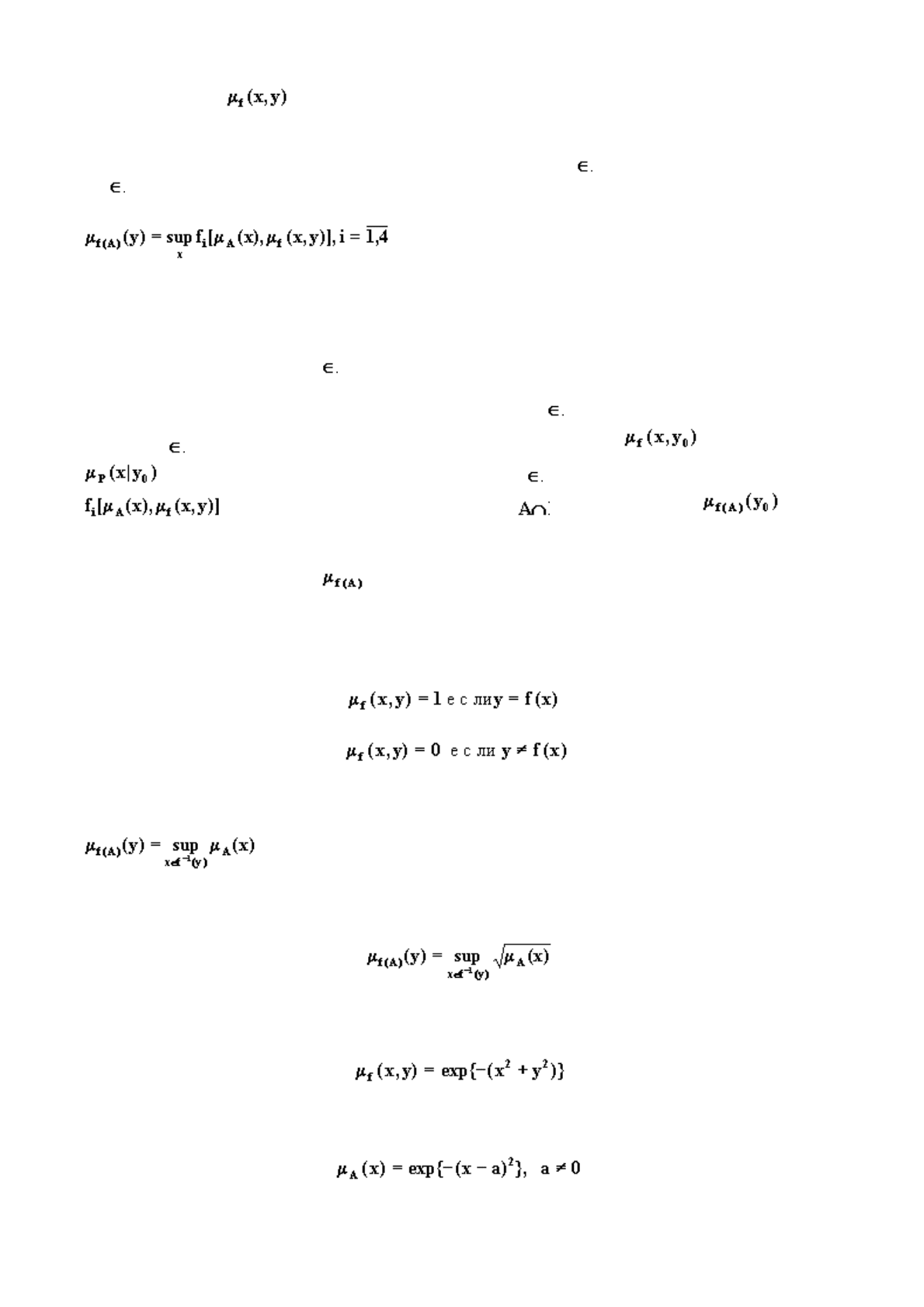
по следующему правилу

, (1.19)

где функция

определяет какую-либо из операций пересечения i-го типа.

Соотношение (1.19) для i=1 получено в работе Заде [98]по аналогии геометрическому способу

построения образа элемента

x X

по графику обычного отображения

f:R

→

роцед

ра

построения множества

f(A

) по (1.19) при

A F(X)

заключается в следующем.

Пусть

- произвольный фиксированный элемент. Тогда есть

-функция

условной проекции первого типа

PF(X)

. Следовательно, выражение

является

-функцией множества

и величина равна

супремуму этой функции на

Таким образом, функция

является рез

льтатом решения параметрической

кстремальной задачи

, в которой в качестве параметра выступает переменная

В частности, если

есть отношение в

∗

, определяющее обычное отображение

f:X

→

, т.е.

то из (1.19) для i=1 ,2,4 следует, что

, (1.20)

а для i=3

Пример 1.9.

Пусть

X=Y=R

f:R

→

определяется следующим

-отношением:

Если

то для i=1 максимум функции по

при произвольном фиксированном

достигается в точке , определяемой из уравнения

ешение которого дает

Подставляя в или в получим

Если

a=0

, т.е. , то очевидно, что определяется из уравнения

т.е. и, следовательно,

Если i=2, т.е. операция пересечения определяется по второму типу, то из уравнения

находим, что и, следовательно,

Пример 1.10.

Пусть снова

X=Y=R

и задано отображение

y=f(x)=x

Если

то учитывая, что имеем

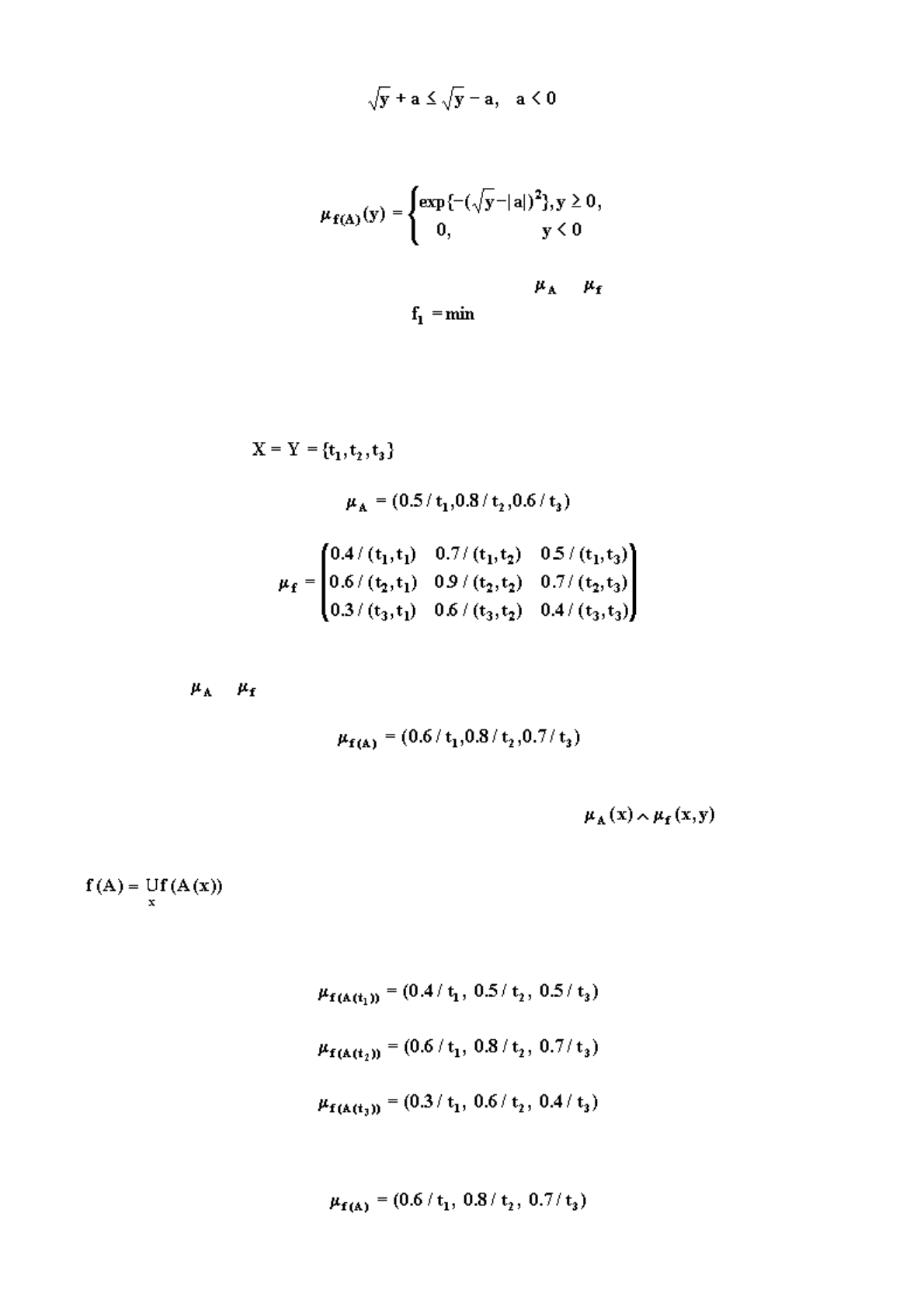
Следовательно, согласно (8.2)

В том случае, когда

- конечные

-множества, т.е. и представимы в виде вектора

и матрицы, то, например, для i=1, т.е. , нахождение

f(A)

сводится

максиминном

произведению вектора на матрицу

В этой операции произведение значений F-функций

аменяется взятием их минимума, а сумма - их максимумом.

Поясним это следующим примером.

Пример 1.11.

Пусть ,

Слева от наклонной черты указывается значение

-функций в соответствующей точке.

Перемножая и по описанному правилу, получим

Этот же результат можно получит другим путем, заметив из (1.19) следующий факт. Если

произвольный фиксированный элемент из

, то

-функция определяет в

(Y)

некоторое множество

f(A(x))

. Тогда

. (1.21)

Для нашего примера имеем

откуда

Исходя из (1.19)-(1.21), Л. Заде сформулировал так называемый

принцип обобщения

который для нечетких множеств представляет собой основное равенство, позволяющее

асширить область определения

отображения или отношения

, включив в нее наряду с

точками произвольные нечеткие подмножества

. Предположим, что

- нечеткое

подмножество вида

Тогда принцип обобщения утверждает, что

, (1.22)

т.е. образ множества

при отображении

можно получить зная образы элементов

при этом отображении.

Во многих приложениях принципа обобщения возникает

следующая проблема. Имеется

функция

переменных и нечеткое множество (отношение)

, характеризующееся функцией принадлежности . Однако во многих

случаях известно не само множество

, а его проекции на

соответственно. В связи с этим возникает вопрос: какое выражение следует

использовать для .

В таких случаях обычно, если нет специально оговоренных ограничений на

переменные

, предполагают, что функция принадлежности отношения

имеет вид

, (1.23)

где ,

i=1,...,n

- функция принадлежности множества

, что эквивалентно предположению

о том, что

- декартово произведение своих проекций., т.е.

Пример 1.12.

Пусть

- арифметическое произведение

, а проекции

определены следующим образом:

примерно

2 = 0,6/1 + 1/2 + 0,8/3,

примерно

6 = 0,8/5 + 1/6 + 0,7/7.

Используя (1.23) и применяя принцип обобщения, имеем:

0,8/5

1/6 0,7/7

0,6/1

0,6/5 0,6/6 0,6/7

1/2

0,8/10 1/12 0,7/14

0,8/3

0,8/15 0,8/18 0,7/21

Таким образом, арифметическое произведение нечетких чисел

примерно

2 и

примерно

6 есть

нечеткое число с найденной функцией принадлежности.

Понятие отображение

-множеств играет исключительно важную роль как в практических

приложениях, так и при введении алгебраических операций над нечеткими величинами.

1.8. Уровневые множества

Определение уровневых множеств совпадает с определением множеств Лебега в теории

измеримых функций.

Если

A F(X)

[0, 1]

, то

слабым

-уровневым множеством

-множества

называется

множество

, (1.24)

сильным

-уровневым множеством

. (1.25)

Нетрудно показать, что уровневые множества обладают следующими свойствами [67]:

10.

Пусть

- множество всех четких подмножеств из

- класс отображений

f: [0,1]

→

со свойствами:

1. ;

f(0)=Х

Тогда справедлива следующая теорема [179].

Теорема 1.3.

Существует биекция

между классами

F(X)

такая, что

)

есть слабое

-уровневое множество для

T(f)

Если же

- введенный класс со свойствами:

1. ;

f(1) равняется пустому множеству

то справедлива аналогичная теорема [166], где

)

будет сильным

-уровневым множеством

для

T(f)

С помощью

-уровневых множеств в дальнейшем формулируются многие важные свойства

F-множеств.

Анализ обширного отечественного [6, 7, 64, 65, 84, 178, 179, 214, 243, 245] и зарубежного

материала [54, 98, 99, 110, 129, 170, 265, 281, 318, 334] по теоретическим и практическим

аспектам теории нечетких множеств показывает, что в еще слабо разработаны численные и

аналитические методы для работы с нечеткими величинами и очень мало работ по

применению этой теории в алгоритмах контроля и управления сложными системами.

Поэтому приведем основные результаты, полученные нами в [38, 72, 134], для обеспечения

вычислительных расчетов с нечеткими величинами. Мы рассмотрим наиболее общие

аналитические и численные методы, позволяющие оперировать с нечеткими величинами.

Понятие нечеткой и интервальной величины вводятся путем обобщения понятия

вещественного числа.

ГЛАВА 2. АЛГЕБРАИЧЕСКИЕ

ОПЕРАЦИИ НАД НЕЧЕТКИМИ

ВЕЛИЧИНАМИ

2.1. Математическая структура базового множества и

свойство выпуклости

В предыдущей главе у базового множества

не предполагалось наличие какой-либо

внутренней математической структуры. Если считать, например, что

- векторное,

топологическое, метрическое или какое-либо другое пространство, то естественно возникает

вопрос, каким образом определенную структуру базового множества можно распространить

на класс

F(X)

Будем полагать,

X=R

- множество вещественных чисел, а элементы класса

F(R)

будем

называть

нечеткими величинами

. Основные задачи, решаемые в данной главе, заключаются

в следующем:

1. Распространить алгебраические операции из

на класс

F(R)

2. Исследовать свойства полученных операций.

3. Показать некоторые аналитические и численные методы нахождения результатов

алгебраических операций над

-величинами.

Величина называется

дискретной

, если множество конечное или счетное.

Если мощность

равна континууму, то величина

называется

непрерывной

Поскольку некоторые пункты исследования тесно связаны с методами решения

экстремальных задач, то основное внимание будем уделять непрерывным

-величинам.

Кроме того, среди всех непрерывных

-величин целесообразно выделить следующие.

Величина

А F(R)

называется

выпуклой

, если для любых и любого

[0,1]

справедливо неравенство

(2.1)

Если в (2.1) равенство возможно только при

, то величина

называется

строго

выпуклой

Пример 2.1.

Пусть

А F(R)

и имеет

-функцию вида

или