Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях

Подождите немного. Документ загружается.

Очевидно, что в обоих случаях

- строго выпуклая

-величина.

Пример 2.2.

Пусть

А F(R)

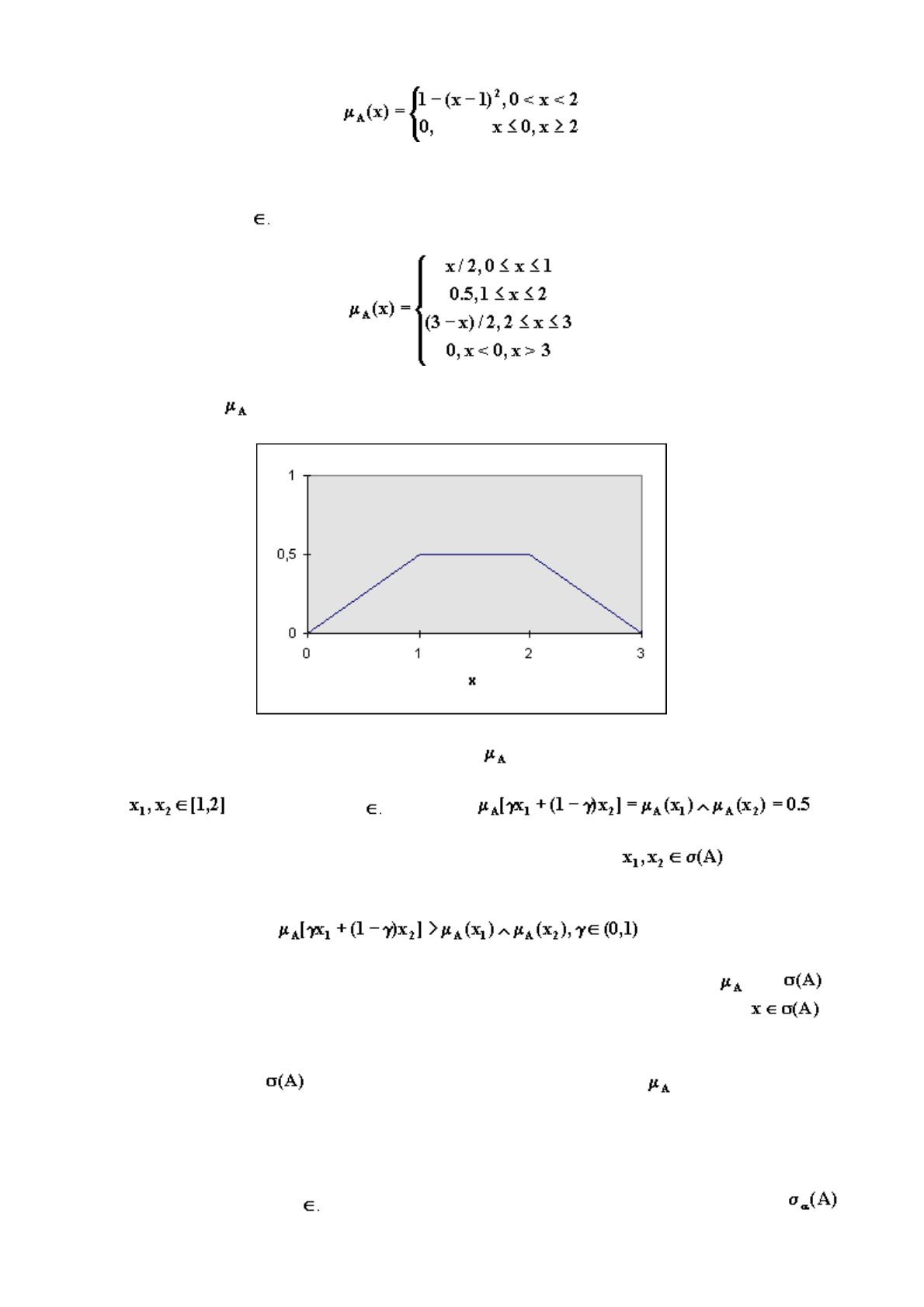
определяется следующим образом:

График функции показан на рис.2.1.

Рис.2.1. График функции для примера 2.2.

Если , то для любого

[0,1]

имеем ,

т.е. А - выпуклая F-величина, поскольку для всех остальных выполняется

неравенство

Нетрудно заметить, что если А - строго выпуклая F-величина, то функция на -

строго возрастающая или строго убывающая; или строго возрастает до некоторого ,

затем строго убывает.

Если

- выпуклая, то может дополнительно иметь участки, где постоянная.

Связь между выпуклыми величинами и их

-уровневыми множествами из

устанавливается

следующей теоремой.

Тео

ема 2.1.

Величина

А F

(

)

вып

кла тогда и только тогда, когда множества

выпуклы для всех .

оказательство

. Пусть величина

А F(R)

- выпуклая. Рассмотрим

-уровневое множество

Если пусто, то оно выпукло. Пусть , т.е. и . Тогд

из условия выпуклости для

получим

В силу того, что следует, что при любом точка

принадлежит , т.е. оно выпукло в

С другой стороны, предположим, что множества выпуклы в

при любом .

Пусть и . Необходимо доказать, что для

Предположим противное, т.е. пусть найдется такое, что

Тогда очевидно, что для любого , , точки . Следовательно,

поскольку по условию теоремы множество - выпуклое, то

должна принадлежать , что не выполняется, т.к. .

Полученное противоречие завершает доказательство.

Аналогичную теорему можно доказать и для слабых

-уровневых множеств.

Следствие

. Учитывая тот очевидный факт, что если

А ,B F(R)

- выпуклые и при этом

выпуклое при любом заключаем,

что - выпуклая

-величина.

ножество

называется

выпуклым

, если для любых точек и из

и любого выполняется неравенство

(2.2)

Если равенство в (2.2) возможно только при

, то

называется

строго выпуклым

Тео

ема 2.2.

Если

А,B F

(

)

- вып

клые, то -вып

клое.

оказательство

. Действительно, если , то

В этом случае, учитывая второе и третье определения, имеем

что и доказывает теорему.

Теорема 2.3.

Если - выпуклое, то его проекции являются выпуклыми.

оказательство

. Пусть ,

-функция одной из проекций и точки и

такие, что и .

Тогда для произвольного имеем:

Выпуклость второй проекции доказывается аналогично.

F-отображение

f: R

→

называется

выпуклым

, если соответствующее ему

-отношение

выпукло в

Теорема 2.4.

Если

f: R

→

выпуклое отображение и

А F(R)

выпуклая величина, то

f(A)

тоже будет выпуклой.

оказательство

. Величина

f(A)

имеет

-функцию

Пусть и такие, что

Тогда для произвольного имеем:

Следствие

. Если

А F(R)

выпуклая величина и

f: R

→

линейная функция, то

f(A)

выпуклая.

Пример 2.3.

Пусть и . В силу взаимной

однозначности отображения f из (1.20) имеем

Пример 2.4.

Пусть и , т.е.

- нелинейное отображение. В

этом случае получим ,

и, следовательно, , т.е. не является выпуклой.

2.2. Алгебраические операции над F- величинами

Операции сложения, умножения, вычитания и деления, определенные на множестве

вещественных чисел, распространяются на класс

F(R)

следующим образом. Каждая из

отмеченных выше бинарных операций на

есть отображение

f: R

∗

→

Если взять теперь два сегмента

A=[a,b]

B=[c,d]

, то их сумма, например, определяется

отображением

f: A

∗

→

которое для запишется в виде

f(x,y) = z = x+y

где . Очевидно, что

A+B = [a+c, b+d]

Теперь становится понятным переход к определению алгебраических операций над

величинами.

Пусть теперь

A, B F(R)

- есть некоторая операция из набора

{+, -, *, /}

. Учитывая

соотношения (1.8) и (1.20) можно записать:

. (2.3)

Если декартово произведение определить по второму типу, то получим

(2.4)

Общий случай для всех четырех типов декартового произведения запишется в виде:

(2.5)

где - какая-либо из четырех типов функций, введенных ранее.

Таким образом, для получения F-функции необходимо решить параметрическую задачу

на нахождение условного экстремума, т.е. в зависимости от

z R

найти верхнюю грань

функции на множестве

, задаваемого ограничением (уравнением связи)

g(x, y; z) = x

y - z = 0.

(2.6)

Необходимо отметить, что решение поставленной задачи всегда существует в отличие от

задачи поиска максимума некоторой функции на заданном множестве [71].

Пример 2.5.

Пусть на

U={x| 0< x<1}

. В этом случае

но точек максимума на

функция

не имеет. Если же

U={x| 0< x 1}

, то

Пример 2.6.

Функция на

U={x| 1< x }

не имеет точек максимума, но

. Если

U={x| 1< x a < }

, то

Вообще говоря, все аналитические и численные методы решения экстремальных задач

предназначены для нахождения локальных максимумов и минимумов [41, 71, 163, 233].

Поэтому, если верхняя грань функции не совпадает с ее глобальным максимумом, то

необходимо п

оводить некото

ые специальные исследования. Хо

ошо известно также, что

успех решения экстремальной задачи во многом зависит от вида целевой функции. Более

подробно эти вопросы будут рассматриваться в последующих разделах.

Прежде чем приступить к исследованию некоторых свойств алгебраических операций над

величинами, следует сделать одно замечание.

Если выразить одну из переменных в (2.6) через другую, например,

через

в виде

y = u(x,z)

то, подставляя полученное выражение для

в (2.5), можно преобразовать данную задачу в

следующую экстремальную задачу без ограничений, содержащую единственную переменную

. (2.7)

Другой подход состоит в использовании множителей Лагранжа. В этом случае задача (2.5) с

учетом (2.6) преобразуется к виду

(2.8)

В дальнейшем, если не оговорено противное, алгебраические операции определяются по

первому типу, т.е. соотношением (2.3).

Алгебраические операции над

-величинами обладают следующими свойствами:

1. Коммутативность сложения и умножения.

Поскольку для всех четырех типов

декартового произведения

а сложение и умножение вещественных чисел коммутативно, то для

A, B F(R)

из (2.5)

следует

A+B=B+A, AB=BA

. (2.9)

2. Ассоциативность сложения и умножения.

Если сложение и умножение определяются по

(2.3) или (2.4), то эти операции ассоциативны, т.е.

(A+B)+C=A+(B+C), (AB)C=A(BC)

. (2.10)

Действительно, если символ * обозначает операцию произведения или взятия минимума, то

. Пусть

где . Тогда

где . Используя (2.7), получим

С другой стороны, поскольку

где , то

где . Следовательно,

Таким образом, . Кроме того, если записать

где , то это можно трактовать как трехместную операцию сложения

-величин. Делая замену , получим, что

(A+B)+C=A+(B+C) =A+B+C

Ассоциативность

множения доказывается аналогично.

3. Дистрибутивность

. В общем случае это свойство операций не выполняется, т.е.

Для получения более точной формулировки закона дистрибутивности необходимо вывести

некоторые соотношения. Покажем сначала, что

, (2.11)

где . Подставляя в (2.11), получим

С другой стороны

где , и следовательно,

Тогда

где , т.е.

что и требовалось доказать. Аналогично показывается, что

, (2.12)

где

Сравним значения функций и в некоторой произвольной точке .

едположим, что такие, что и, к

оме того,

Если положить , то на основании равенства

из (2.12) следует, что не исключена возможность существования таких с условием

, что

и, следовательно,

. (2.13)

Рассмотрим частный случай, когда . Из (2.11) получим

при условии , откуда

. (2.14)

Соответственно, из (2.12) имеем

, (2.15)

при условии . Сравним (2.14) и (2.15) в некоторой произвольной точке , которой

соответствует такая, что

Рассмотрим соотношение ,

из которого следует . (2.16)

Рассмотрим следующие случаи.

1. Числа

одного знака, т.е. . Тогда из (2.16) получаем, что

или . Если при этом

- выпуклая

-величина, то очевидно, что при

поскольку при всех других с указанными выше положениями относительно точки

справедливо неравенство

Наглядное представление этому дает рис 2.2.

Рис.2.2. График для выпуклой функции .

Если А не является выпуклой, то ясно, что могут найтись такие точки , что

и справедливо неравенство

Учитывая дополнительно, что при получаем ,

окончательно получаем, что

Наглядное представление сказанному

дает рис. 2.3.