Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.


450
R.
W.
Ogden
Taken together, equations
(56)-(60)
constitute the basic boundary-
value problem of incremental elasticity when the underlying defor-
mation
x
is known. We next examine the question
of
uniqueness of
solution of the incremental problem and the associated question
of
stability of the deformation
x.
3.1
Uniqueness
and
Stability
Let
X
and
X*
be two possible solutions of the incremental problem
and let
Ax
=
X*
-
jl
(61)
denote their difference. More generally, we adopt the notation A(-)
to represent
(a)*
-
(.).
Then
Ad,
=
GradAx, AS
=
d'AA,
(62)
and hence
DivAS
=
0
in
&,
On use of the divergence theorem it follows that
Clearly,
a
suficient
condition
for uniqueness
of
solution of the
incremental problem is
1,
tr(ASAA)dV
>
0,
for
all
AX
+
0
in
B,
and satisfying AX
=
0
on
8BF,
or,
equivalently,
tr{(d'AA)AA}dV
>
0.
J,

Nonlinear Elasticity
45
1
Note that this sufficient condition applies when the boundary
conditions are inhomogeneous (i.e.
i
#
0,
d-
#
0
in
(56)-(57))
so
in
considering incremental uniqueness it suffices henceforth to examine
the homogeneous boundary-value problem
DivS
=
0
in
B,,
(69)
x
=
0
on
as;,
ST^
=
o
on
a~;,
one solution of which is
x
=
0.
inequality
(67)
becomes
Thus, on setting
x*
=
0,
the
and
(68)
similarly becomes
for all
jl
f
0
in
f?,
satisfying
x
=
0
on
af?;.
If
(73)
holds in the configuration
f?
then the only solution
of
the
homogeneous incremental problem is the trivial solution
2
=
0;
cor-
respondingly, the solu tioii of the inhomogeneous problem is unique
(assuming it exists). Expressed otherwise,
(73),
or equivalently
(67),
excludes bifurcation from the solution
x
of
the underlying boundary-
value problem. The inequality
(73),
or
equivalently
(72)’
is there-
fore referred to as the
exclusion
condition
(for the dead-load traction
boundary condition). The exclusion condition requires modification
if
u
is allowed to depend on the deformation.
To
see why we take
‘
>
0
’
rather than
‘
<
0
’
in
(73)
we consider
the change in the energy functional due to the change in deforma-
tion from
x
to
x’.
On use of the boundary condition
(70)
and the
divergence theorem this is seen to be
E{x’}
-
E{x}
=
/
{W(A’)
-
W(A)
-
tr(SA)}dV.
(74)
fir

452
R.
W.
Ogden
By
application
of
the Taylor expansion to
W(A')
this then becomes
E{x'}
-
E{x}
=
1
{
;tr[(d'A)A]
+
.
,
.}dV
Br
(75)
Thus, to the second order in
A,
(73)
implies that
E{x'}
>
E{x}
for all admissible
jL
$
0
satisfying
(70).
This inequality states that
x
is
stable
with respect
to
perturbations
j(
from
x,
and that
x
is
a
local minimiser
of
the energy functional.
For full discussion
of
infinitesimal
stability we refer to
[20].
Suppose now that we restrict attention to the all-round dea.d-load
problem
so
that
aB:
=
8,
dB,
=
8s:.
If
the underlying deformation
is homogeneous then
A
is independent
of
X
and, therefore,
so
is
A'.
It then follows that
(73)
is equivalent to the local condition
tr{(A*A)A}
>
0
(76)
for all
A
#
0,
i.e.
A'
is
positive definite at each point
X
E
B,.
In order to illustrate loss of uniqueness and stability we now con-
centrate attention on the dead-load traction boundary-value problem
in which the deformation is homogeneous,
so
that
(76)
is the relevant
exclusion condition.
4
Bifurcation from a Homogeneous Defor-
mation under Dead-load
Let
us
imagine
a
path
of
dead-loading from the unstressed configu-
ration in S-space resulting in
a
path of deformation in A-space along
which
A'
is positive definite, i.e. along which
x
is
locally (infinites-
imally) stable
so
that
(76)
holds.
(Note, however, that,
as
we see
shortly,
(76)
does
not hold at the origin
A
=
I
in A-space from which
the path starts.) The inequality first fails,
if
at
all,
when
a
point is
reached where
for
all
A,
with equality holding for some
A
#
0.
By
the estremal
property of quadratic forms it follows that
tr{(A'A)A}
2
0
(77)
AIAe
=
0
(78)

Nonlinear Elasticity
453
for the
A,
which minimises
(77).
Note, however, that
in
general there
may be more than one
A,
satisfying (78). Points
in
A-space where
(78)
holds are given by
det(A')
=
0,
(79)
where we are regarding
d1
as
a
linear mapping
on
the vector space
of second-order tensors
A.
Equation
(79)
describes
a
hypersurface
in A-space and can be regarded as the stability limit or bifurcation
surface since, on this surface,
S,
A'A,
=
0.
(80)
Following the terminology of Hill
[8,9]
we
refer to
A,
as
an
eigenmode
(an eigenvector of
A'
associated with zero eigenvalue) and the sur-
face
as
an
eigensurface.
Bifurcation occurs since, to the first order
in
A,
A
and
A'
=
A
+
A
correspond to tlie same state
of
stress
S.
In
Figure
1
we depict the stable region of A-space bounded by surfaces
on which
(79)
holds together with
a
path of deformation emanating
from
A
=
I
and terminating at
a
point
on
such
a
surface.
Clearly, in the dead-load traction problem,
local
bifiircation
oc-
curs where
A'
is
singular.
Since, in
(77),
equality holds for
A
=
A,
the stability criterion
(76)
is inappropriate to determine the stabil-
ity status of points on the eigensurface. Referring to
(75)
we see
that stability is determined by the sign of the integrmd for
A
=
A,,
and that this is dependent on third- and liigher-order terms
in
A,;
we do not pursue the details here.
Glohnlly,
different branches of
the solution of the dead-load problem can be found by inverting the
stress-deformation relation
(21)
for an unconstrained material or
(22)
for an incompressible material. Before examining this inversion we
consider the singularities of
A'
for an isotropic elastic material.
For an isotropic elastic material the components of
A'
referred
to the principal axes
u(;)
and
di)
are given by

454
R.
W.
Ogden
A=l
1
DEFORMATION
Figure
1:
Depiction of the region
of
sta.bility in A-space.
A!..
13
13
.
+
A!.
1931
..
=
W;;
-
W;j
i
#
j,
A.
1-
-
Xj,
(84)
where
W;
=
aW/aX;,
Wjj
=
d2W/aX;aAj
and
i,
j
E
{1,2,3},
and
no
summation is implied by the repetition
of
indices. (We have now
dropped our convention
of
using Greek letters
for
indices relating
to Lagrangean components.) For details
of
the derivation
of
these
components we refer to
[14].
In the classical theory
of
elasticity, corresponding to the situa.tion
in which there
is
no underlying deformation, the components of
A'
can be written compactly in the form
where
X
and
p
are the classical
Lame'
moduli of ela.sticity and
6;j
is
the Kronecker delta. The values
of
Wjj
when
Xi
=
1
for
i
E
{1,2,3}
should be consistent with
(85).
Also, we ta.ke
W'i
=
0
when
Xj
=
1

Nonlinear Elasticity
455
for
i,j
E
{1,2,3}
so
that the configuration
B,
is stress free; such
a
configuration is called
a
natural configuration.
Necessary and sufficient conditions for
(76)
to hold are
W;j
is
positive definite,
(86)
(87)
rv;
+
rvj
>
0
i,j
E
{1,2,3},
i
#
j,
w;
-
rvj
xi
-
xj
>o
i#j
jointly, while singularities
of
A'
are identified by one or more of the
equations
det(lV;j)
=
0,
(89)
Wj+Wj=O
i+j,
(90)
The form of
W
is critical in deciding whether (S9)
or
(91)
can hold,
but
(90)
must hold on some surfaces in A-spa.ce irrespective
of
the
form
of
W
since the principal Biot stresses
tt
=
Wi
can
take both
positive and negative values (i.e. an elastic material can be subjected
to both tensile and compressive stresses). In particuhr, as indicated
above,
(90)
holds in the natural configuration
A
=
I.
The purpose
of
the above discussion was to show that
A'
can possess singularities,
and we do not examine here the associated eigenmodes; the latter
are studied in detail in
[14,
page
3691.
For incompressible materials, bearing in mind the difference be-
tween
(52)
and
(53),
the components
of
d'
have the sa.me form
as
in
(81)-(84),
but are subject to
(10).
In
this ca.se, however, when
A;
=
1
for
i
E
{
1,2,3}
the components are given by
2'33
'331
i
#
j,
(93)
A!
...
=A!
...
=
0
and
Wj;
=
W;
=
p,
1V;j
=
0,
where
11
is the
shew
modulus
in
B,.
material is
The analogue
of
the stability inequality
(76)
for an incompressible
tr{(d'A)A}
+
ptr(A-'AA-IA)
>
0.
(94)

456
R.
W.
Ogden
Necessary and sufficient conditions for this to hold for an isotropic
elastic material are given in
[14,
page
4501.
4.1
Global
Aspects
of
Non-uniqueness
The singularities of
A'
considered above
are
local manifestations
of non-uniqueness in the relationship between
S
and
A
expressed
through the constitutive equation
dW'
S
=
-(A)
dA
(95)
(for an unconstrained material). We now examine briefly the global
inversion of
(95).
First, we have from
(34)l
s
=
T'R~,
(96)
from which it follows that
and
det
S
=
det
T
=
ti
titi.
Unlike
(4),
however, the polar decomposition
(96)
is not in general
unique since
T'
is not sign definite. For
a
given
S
there are in general
four
distinct polar decompositions of the form
(96),
and
infinitely
many when
(t;')*
=
(tf)2
(i
#
j),
but at most one of these satisfies
the stability inequality
(87).
For each such polar deconiposition
R
is
determined (at least to within an arbitrary rotation about
a
principal
axis) and
U
can
in principle be found by inverting
(25),
an inversion
which itself may not be unique. The resulting deformation gradients
are then calculated from
A
=
RU.
For further discussion of these
points we refer to
[14,
pages
358-3G11.
In order to illustrate the non-uniqueness more explicitly it suffices
to take
R
=
I
and to examine the inversion of
(25)
or
(26).
More
particula.rly, we consider the pure strain
A
=
U
in
which
u(~)
are

Nonlinear Elasticity
457
fixed in direction
as
the load increases.
The problem then reduces
to inverting the scalar equations
(32)
or
(33).
The mathematics can
be associated with the physical problem in which
a
cuboid of elastic
material is subjected to normal forces
1;'
per unit reference area on
its three pairs
of
faces,
as
in the following exa.mple.
4.2
A
Two-dimensional Example
For purposes of this example we consider
an
incompressible material
and rewrite
(33)
in
the form
(99)
81V
ax;
X.t1
xi---
-y
i
E
{1,2,3},
a
'a
with
X1X2X3
=
1.
On elimination of
y
from
(99)
we obtain
Equations
(loo)-(
101)
provide three
equatioiis
for
XI,
A*,
A3
when
t:,ti,ti
are prescribed. Alternatively, if
A3
is given, along with
ti
and
ti,
then
X1
and
X2
and hence
ti
can be found.
For
simplicity
we consider this latter situation with
A3
=
1,
so
that it remains to
determine
X1
and
A2
from the two equations
On introducing the change
of
variables A1
=
X,X2
=
A-'
and the
notation
i@(xj
=
w(x,
A-l,
1)
(103)
we can reduce equations
(102)
to
subject to
I@'(
1)
=
0,

458
R.
W.
Ogden
where the prime indicates differentiation with respect to
A.
further specialization
ti
=
ti
(=
tl,
say) reduces (104) to
The
(A
-
X-’)t’
=
XWl(X).
(106)
The problem is now two-dimensional and we take the cuboid to have
a
square cross-section in the (1,2)-plane. We require to determine
X
when the dead-load traction
t’
is given.
Noting (105),
we
see that, independently
of
tl,
X
=
1
is always
one solution of (106); this corresponds to the situa.tion
in
which the
square cross-section remains unchanged
as
t’
increases from zero.
We wish, however,
to
consider the possible emergence of solutions of
(106) for which
X
#
1.
To
this end we rewrite (106) in the form
In
the limit
X
+
1
this becomes
(
108)
which is the (positive) shear modulus of the material. The stress
t:
is
a
criticd
due
of
t’
in the sense that it
is
the value at which
bifurcation from the symmetrical solution
X
=
1
call occur. This can
be seen by expanding (107)
as
a
Taylor series near
X
=
1
to give
1-
2
2;
=
-Ivy
1)
=
p,
t’
=
t;
+
q(X
-
1)2
+
. . .
,
(109)
1
12
where
q
=
-fiyl)
-
W”(1).
Note that it can be shown that
dt’/dX
=
0
at
X
=
1.
Equation (109) shows that
a
synimetry-breaking bifurcation can
emerge in which the square cross-section becomes rectangula,r. [We
do not consider here possible complications associated with rotation
of
the principal axes and the inclusion of
R
in the equations.) The
sta-
bility inequality (94) for this two-dimensional problem can be shown
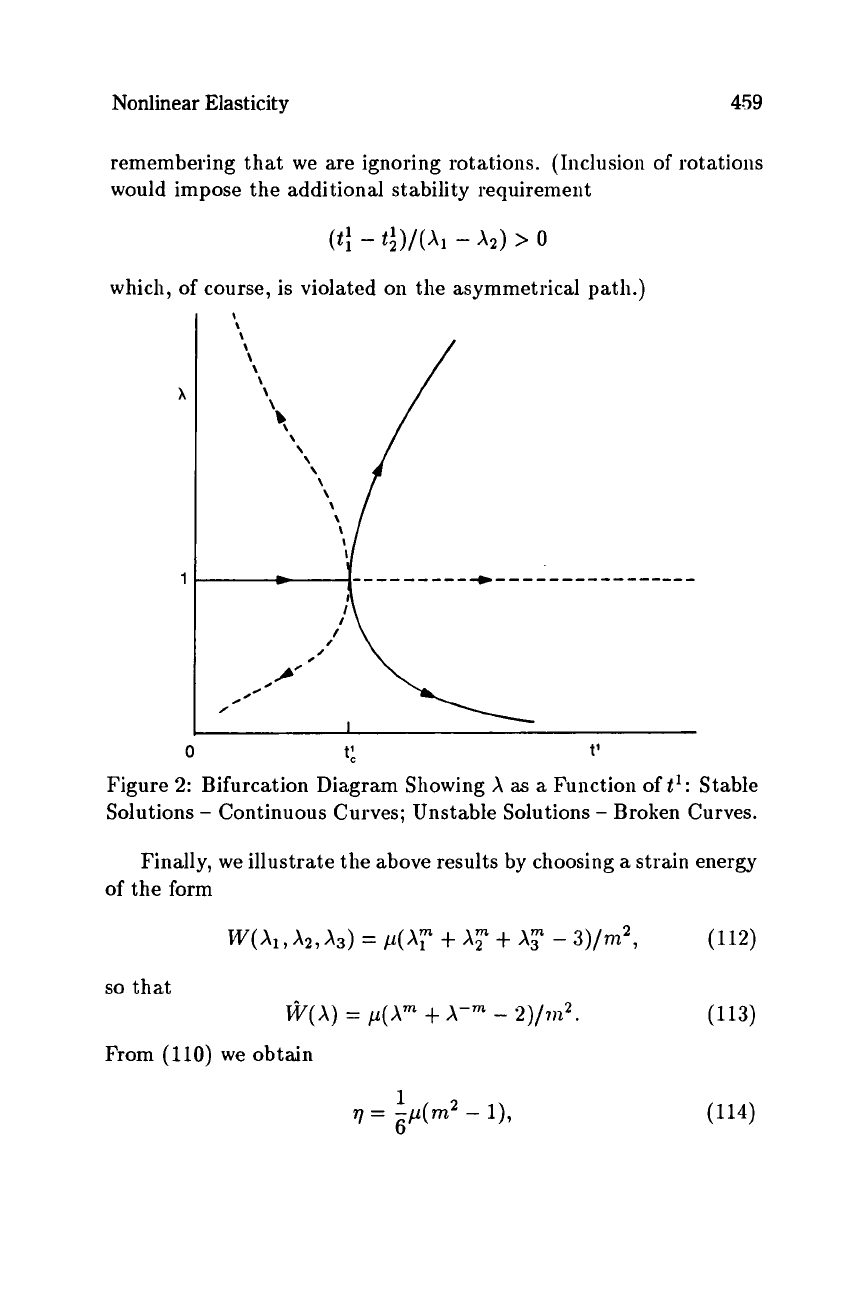
Nonlinear Elasticity
459
remembering that we are ignoring rotations. (Inclusion
of
rotations
would impose the additional stability requirement
(t:
-
ti)/(Xl
-
X2)
>
0
which,
of
course, is violated on the asymmetrical path.)
0
t:.
t'
Figure
2:
Bifurcation Diagram Showing
X
as
a
Function oft': Stable
Solutions
-
Continuous Curves; Unstable Solutions
-
Broken Curves.
Finally, we illustrate the above results by choosing
a
strain energy
of
the form
so
that
@(A)
=
p(P
t
A-"
-
2)/7n2.
(113)
From
(110)
we obtain
(114)
77=
gp(m
12
-
11,
