Анищенко В.С. Нелинейные эффекты в хаотических и стохастических системах
Подождите немного. Документ загружается.

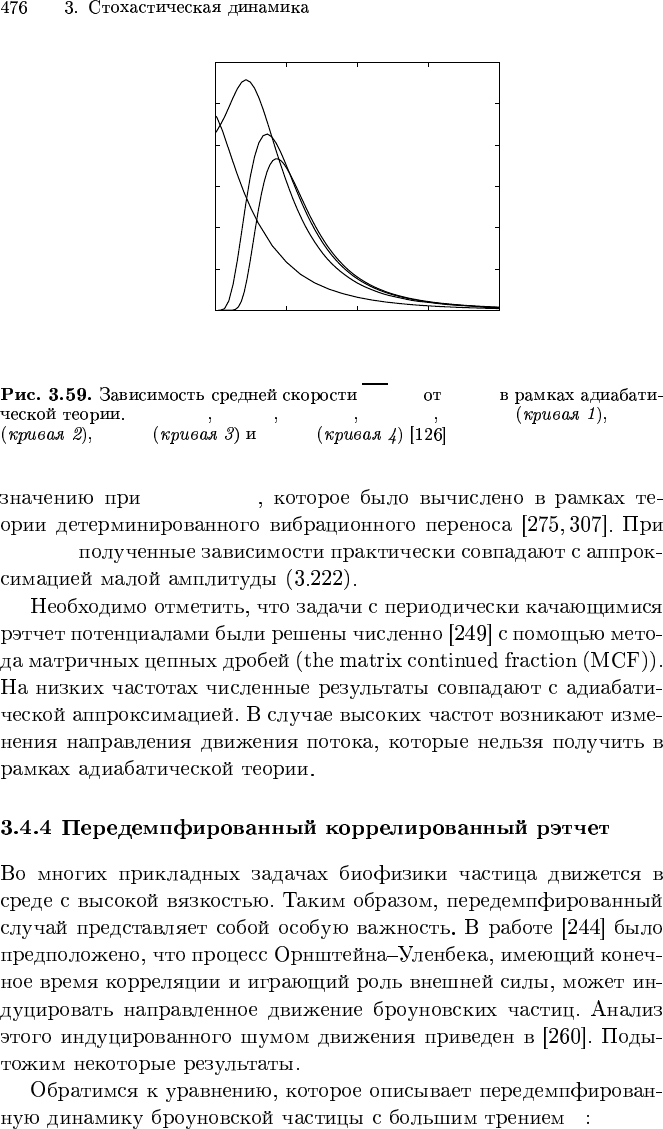
0
0.01
0.02
0.03
0.04
0.05
0.06
0 0.5 1 1.5 2
<x>/B
2
D/U
0
1
2
3
4
.
|
h ˙xi/A
2
D/U
0
a
1
= 1.25 a
2
= 5 x
1
= 0.8 x
2
= 0.2 A = 0.1 A = 1
A = 2 A = 5
D/U
0
→ 0
A < 0.5
γ

˙x =
1
γ
−V
0
(x) + F + y(t) +
√
2Dξ(t)
.
y(t)
hy(t)y(t
0
)i =
Q
τ
exp
|t −t
0
|
τ
,
τ Q
h˙xi J
0
= h˙xi/L
x, y
50
Q τ F = 0 γ = 1
U(x) =
1
(2π)
[sin(2πx) + 0.25 sin(4πx)] .
Q τ
hy
2
i = 0 τ
Q
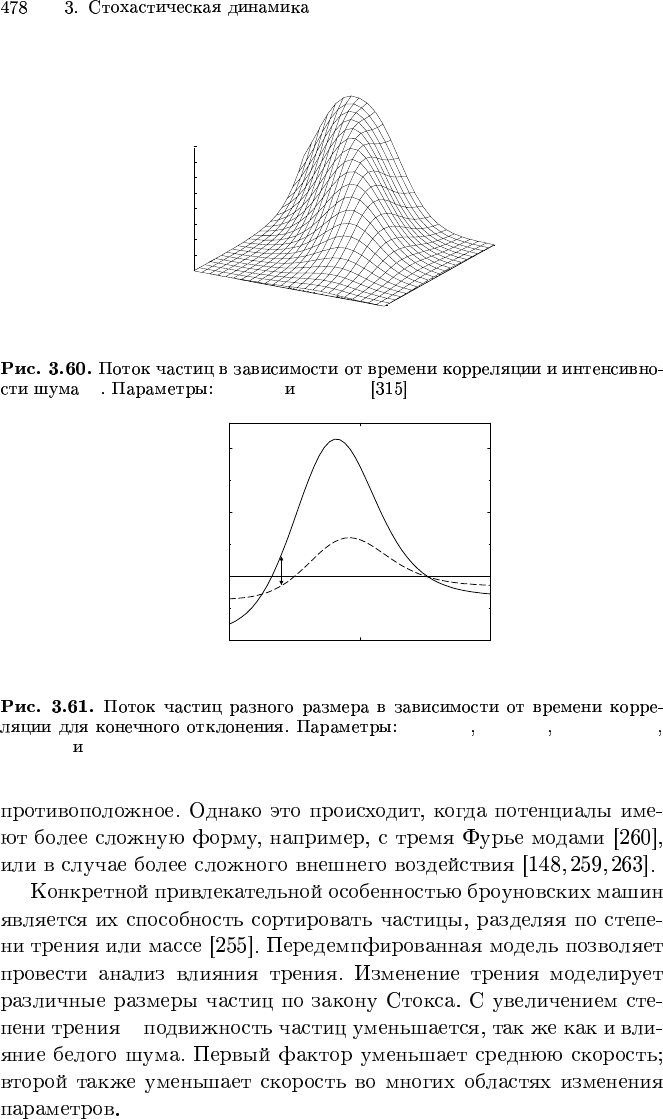
0.01
0.1
1
10
0.01
0.1
1
10
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
Q
tau
Q γ = 1.0 D = 0.1
10
−2
10
0
10
2
τ
−0.005
0
0.005
0.01
D = 0.1 Q = 0.2 F = −0.005
γ
1
= 1.0 γ
2
= 2.0
γ

F 6= 0
τ = 0.1
x v
m γ
˙x = v, m ˙v = −γv −U
0
(x) + F + y(t) +
√
2Dξ
1
(t).
y(t)
ξ
1
(t)
D
˜
t =
t
t
0
, ˜x =
x
x
0
, ˜v =
vt
0
x
0
, ˜y =
yV
0
x
0
, V (˜x) =
U(x)
V
0
,
˜
F =
x
0
F
V
0
,

V V (˜x) =
V (˜x + 1)
t
0
= γx
2
0
/V
0
µ =
mV
0
x
2
0
γ
2
,
˜
D =
D
V
0
γ
,
˜
Q =
Q
V
0
γ
, ˜τ =
τV
0
γx
2
0
.
˙x = v, µ ˙v = −v −V
0
(x) + F + y(t) +
√
2Dξ
1
(t), ˙y = −
y
τ
+
√
2Q
τ
ξ
2
(t)
˜
hvi
∝ 1/γ
τ
x, v, y

x
τ
µ → ∞
˙x =
1
g(x)
−V
0
(x) + F +
p
2(Q + D) ξ(t)
,
g(x)
g(x) = 1 +
d
dx
τ Q [V
0
(x) − F ]
(D + Q)(1 + µ/τ) + τ V
00
(x)
.
J hvi = h˙xi = J
h˙xi =
L (Q + D)
h
1 − exp
Φ(1)/(Q + D)
i
1
R
0
dx g(x) exp
− Φ(x)/(Q + D)
x+1
R
x
dy g(y) exp
Φ(y)/(Q + D)
.
Φ(x) =
Z
x
0
g(y) [V
0
(y) − F ] dy.
τ → 0 g(x) → 1
h˙xi
τ=0
F 6= 0 µ 0 < τ <
∞
V (x) F = 0
τ F = 0
h˙xi = −
ˆτ
2
Q
A(0)(D + Q)
2
Z
1
0
V
0
(y)V
00
(y)
2
dy,
A(F ) =
1
Z
0
dx
x+1
Z
x
dy exp
[V (y) − V (x) + (x − y)F ]/(D + Q)
.

ˆτ = τ/(1+µ/τ)
µ
µ
τ
ˆτ
0.1 1.0
τ
0.001
0.01
0.1
<v>
0.1 1.0
τ
0.001
0.01
0.1
<v>
h˙xi = k
+
− k
−
,
k
+
k
−
k
±
= ζ
±
exp −∆Φ
±
/D ∆Φ
±
D x
#

V (x) − xF x
+
x
−
= x
+
−1
τ
∆Φ
±
(τ) = ∆Φ
(0)
±
+ ∆Φ
(1)
±
(τ)
=
V (x
#
) − V (x
±
) + (x
±
− x
#
)F
1 + R
+ τ
2
R
(1 + R)
2
Z
∞
−∞
¨q
2
±
(t) dt
R = Q/D q
±
(t)
µ¨q
±
(t) =
−˙q
±
(t) − V
0
(q
±
(t)) + F
t → ∞
ζ
±
ζ(τ) ' ζ(τ = 0) (D + Q)
h˙xi = k
0
+
[ exp (−∆Φ
(1)
+
/D)−exp (−[∆Φ
(1)
−
+LF/(1+R)]/D)],
k
0
+
= k
+
(τ = 0) ∆Φ
(0)
+
∆Φ
(1)
+
−∆Φ
(1)
−
µ
µ 1
k
±
τ = 0.5
τ
µ

P (x, v, y)
v y
x
Q
Q
D
0.01
1
100
µ
0.01
1
100
τ
0
0.004
0.008
0.012
<v>
0.01
1
100
µ
0.01
1
100
τ
0
0.004
0.008
0.012
<v>
Q/D < 1 Q/D > 1 Q D
µ → ∞
τ µ
τ
µ
µ τ
µ ≈ 0.1
µ τ
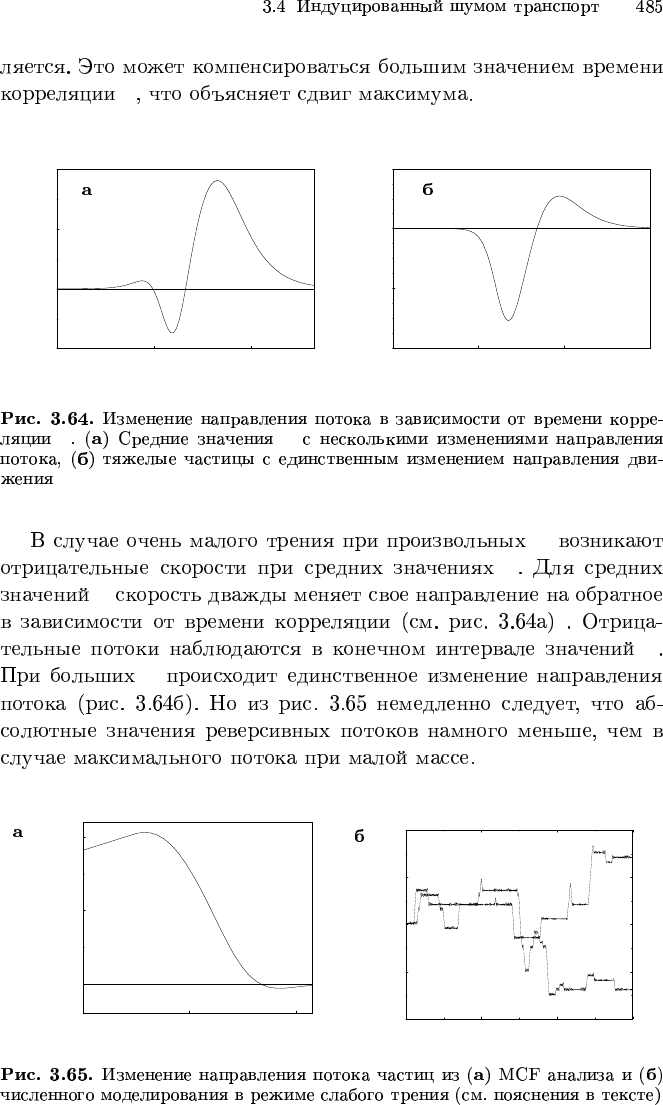
τ
10
−2
10
0
10
2
τ
−5
.
10
−5
0
5
.
10
−5
10
−4
<v>
10
−2
10
0
10
2
10
4
τ
−4
.
10
−5
−2
.
10
−5
0
2
.
10
−5
<v>
τ µ
R
τ
µ
τ
µ
10
−2
10
0
10
2
µ
0.000
0.001
0.002
<v>
0 2000 4000 6000
t
−20
−10
0
10
20
x(t)
