Balakumar Balachandran, Magrab E.B. Vibrations

Подождите немного. Документ загружается.

3.3.1 Natural Frequency

Translation Vibrations: Natural Frequency

For translation oscillations of a single degree-of-freedom system, the natural

frequency v

of the system is deﬁned as

(3.14)

where k is the stiffness of the system and m is the system mass. The quantity

, which is also referred to as the natural frequency, has the units of Hz.

For the conﬁguration shown in Figure 3.1, the vibratory system exhibits

vertical oscillations. For such oscillations, we make use of Eq. (3.6) and

Eq. (3.14) and obtain

(3.15)

where is the static deﬂection of the system.

Rotational Vibrations: Natural Frequency

Drawing a parallel to the deﬁnition of natural frequency of translation mo-

tions of a single degree-of-freedom system, the natural frequency for rota-

tional motions is deﬁned as

(3.16)

where k

is the torsion stiffness of the system and J is the mass moment of in-

ertia of the system.

 2pf



rad/s

 2pf



rad/s

 2pf



rad/s

80 CHAPTER 3 Single Degree-of-Freedom Systems

Design Guideline: For single degree-of-freedom systems, an in-

crease in the stiffness or a decrease in the mass or mass moment of in-

ertia increases the natural frequency, whereas a decrease in the stiffness

and/or an increase in the mass or mass moment of inertia decreases the

natural frequency. Equivalently, when applicable, the greater the static

displacement the lower the natural frequency; however, from practical

considerations too large of a static displacement may be undesirable.

Period of Undamped Free Oscillations

For an unforced and undamped system, the period of free oscillation of the

system is given by

(3.17)

Thus, increasing the natural frequency decreases the period and vice versa.

T 



In the following examples, we show how the static displacement can be

used to determine the natural frequency of a single degree-of-freedom system.

EXAMPLE 3.4

Natural frequency from static deﬂection of a machine system

For a particular choice of machinery mounting, the static deﬂection of a piece

of machinery is found to be . For two other choices of machin-

ery mounting, this deﬂection is found to be and .

Based on the static deﬂection, we will determine the natural frequency for

vertical vibrations for each of the three machinery mountings. To this end, we

make use of Eq. (3.15). Noting that the acceleration due to gravity g 

9.81 m/s

, we arrive at the following for the natural frequencies of the three

machinery mountings:

EXAMPLE 3.5

Static deﬂection and natural frequency of the tibia bone in a human leg

Consider a person of 100 kg mass standing upright. We shall determine the

static deﬂection in the tibia bone and an estimate of the natural frequency of

axial vibrations. The tibia has a length of 40 cm, and it is modeled as a hol-

low tube with an inner diameter of 2.4 cm and an outer diameter of 3.4 cm.

The Young’s modulus of elasticity of the bone material is .

The static deﬂection will be determined by using Eq. (3.6), and Eq. (3.15)

will be used to determine the natural frequency. We assume that both legs

support the weight of the person equally, so that the weight supported by the

tibia is

(a)

To determine the stiffness k of the tibia, we use Case 1 of Table 2.3 to obtain

(b) 22.78  10

N/m

k 



12  10

N/m

2

313.4  10

2

 12.4  10

2

40  10

2

mg  a

100

kg b 19.81 m/s

2 490.5 N

2  10

N/m



2p B

st 3



2p B

9.81 m/s

10  10

3

 4.98 Hz



2p B

st2



2p B

9.81 m/s

1  10

3

 15.76 Hz



2p B

st1



2p B

9.81 m/s

0.1  10

3

 49.85 Hz

st3

 10 mmd

st2

 1 mm

st1

 0.1 mm

3.3 Natural Frequency and Damping Factor 81

Hence, from Eqs. (3.6), (a), and (b), the static deﬂection is given by

21.53 m (c)

and, from Eqs. (3.15) and (c), the natural frequency is

(d)

EXAMPLE 3.6

System with a constant natural frequency

In many practical situations, different pieces of machinery are used with

a single spring-mounting system. Under these conditions, one would like for

the system natural frequency to be constant for the different machinery-

mounting-system combinations; that is, we are looking for a system whose

natural frequency does not change as the system mass is changed. Through

this example, we examine how the spring-mounting system can be designed

and discuss a realization of this spring in practice.

From Eq. (3.14), it is clear that the natural frequency depends on the mass

of the system. In order to realize the desired objective of constant natural fre-

quency regardless of the system weight, we need a nonlinear spring whose

equivalent spring constant is given by

(a)

where A is a constant, the weight W  mg, and g is the gravitational constant.

Then, from Eqs. (3.15) and (a), we arrive at

(b)

from which it is clear that the natural frequency is constant irrespective of the

weight of the mass.

Nonlinear Spring Mounting

When the side walls of a rubber cylindrical tube are compressed into the non-

linear region,

the equivalent spring stiffness of this system approximates the

characteristic given by Eq. (a). For illustrative purposes, consider a spring that

has the general force-displacement relationship

(c)

where a and b are scale factors and c is a shape factor. Noting that for a ma-

chinery of weight W, the static deﬂection x

is determined by using Eq. (c) as

F1x 2 a a



2p B



2p B



2Ag

k  AW



2p B



2p B

9.81 m/s

21.53 m

 107.4 Hz



490.5 N

22.78  10

N/m



82 CHAPTER 3 Single Degree-of-Freedom Systems

E. I. Riven, Stiffness and Damping in Mechanical Design, Marcel Dekker, NY, pp. 58–61

(1999).

(d)

For “small” amplitude vibrations about x

, the linear equivalent stiffness of

this spring is determined from Eqs. (c) and (d) to be

(e)

Then, from Eqs. (3.14) and (e), we determine the natural frequency of this

system as

(f)

Representative Spring Data

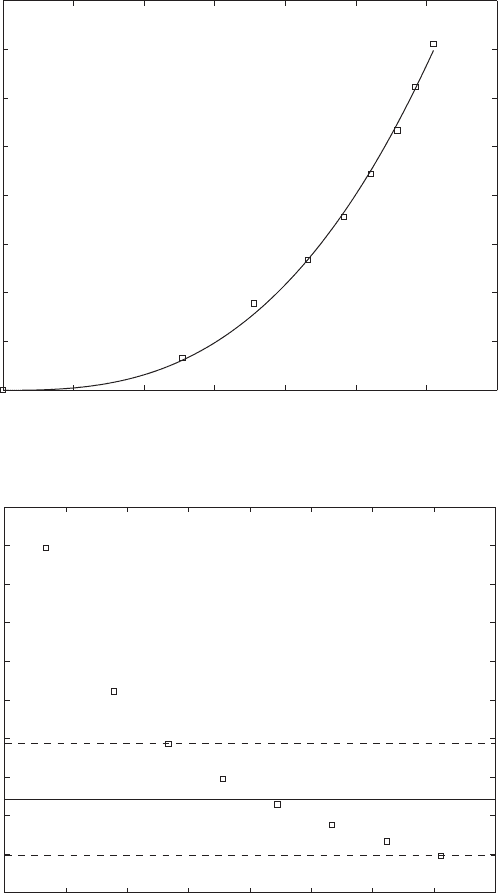
We now consider the representative data of a nonlinear spring shown in

Figure 3.5a. By using standard curve-ﬁtting procedures,

we ﬁnd that a 

2500 N, b  0.011 m, and c  2.77. After substituting these values into

Eq. (f), we arrive at the natural frequency values shown in Figure 3.5b. It

is seen that over a sizable portion of the load range, the natural frequency of

the system varies within the range of 8.8%. The natural frequency of

a system with a linear spring whose static displacement ranges from 12 mm

to 5 mm varies approximately from 4.5 Hz to

7.0 Hz or approximately 22% about a frequency

of 5.8 Hz.

3.3.2 Damping Factor

Translation Vibrations: Damping Factor

For translating single degree-of-freedom systems, such as those described by

Eq. (3.8), the damping factor or damping ratio z is deﬁned as

(3.18)

where c is the system damping coefﬁcient with units of Ns/m, k is the system

stiffness, and m is the system mass. The damping factor is a nondimensional

quantity.

z 

2mv



22km



129.8/0.005

/2p Hz 2

129.8/0.012

/2p Hz 2



2p B

1/12c2



2p B

W/g



2p B

1/c



1c12/c



dF1x 2

x x



c1

 b a

1/c

3.3 Natural Frequency and Damping Factor 83

The MATLAB function lsqcurveﬁt from the Optimization Toolbox was used.

0 0.002 0.004 0.006 0.008 0.01 0.012 0.014

500

1000

1500

2000

2500

3000

3500

4000

x (m)

W (N)

(a)

0 500 1000 1500 2000 2500 3000 3500 4000

7.5

8.5

9.5

10.5

11.5

(Hz)

W (N)

(b)

FIGURE 3.5

(a) Curve ﬁt of nonlinear spring data: squares– experimental data values; solid line– ﬁtted curve;

(b) natural frequency for data values in (a) above: horizontal broken lines are within 8.8% from

the solid horizontal line.

3.3 Natural Frequency and Damping Factor 85

Critical Damping, Underdamping, and Overdamping

Deﬁning the quantity c

, called the critical damping, as

(3.19)

the damping ratio is rewritten in the form

(3.20)

When . The signiﬁcance of c

is discussed in Section 4.2, where

free oscillations of vibratory systems are considered. A system for which

is called an underdamped system and a system for which is

called an overdamped system. A system for which is called a critically

damped system.

Rotational Vibrations: Damping Factor

For rotating single degree-of-freedom systems such as those described by

Eq. (3.13), the damping ratio z is deﬁned as

(3.21)

where the damping coefﬁcient c

has the units Nms/rad.

From Eqs. (3.14) and (3.16), we see that the stiffness and inertia proper-

ties affect the natural frequency. From Eqs. (3.18) and (3.21), we see that

the damping ratio is affected by any change in the stiffness, inertia, or damp-

ing property. However, one can change more than one system parameter in

such a way that the net effect on z remains unchanged. This is shown in Ex-

ample 3.8.

Governing Equation of Motion in Terms of Natural Frequency

and Damping Factor

Introducing the deﬁnitions given by Eqs. (3.14) and (3.18) into Eq. (3.8), we

obtain

(3.22)

The signiﬁcance of the quantities v

and z will become apparent when the

solution to Eq. (3.22) is discussed in detail in the subsequent chapters. If we

introduce the dimensionless time , then Eq. (3.22) can be written as

(3.23)

It is seen from Eq. (3.23) that the natural frequency associated with the non-

dimensional system is always unity (one), and that the damping factor z is the

only system parameter that appears explicitly on the left-hand side of the equa-

tion. We shall use both forms of Eqs. (3.22) and (3.23) in subsequent chapters.

 2z

 x 

f 1t2

t  v

 2zv

 v

x 

f 1t 2

z 

2J v



22k

z  1

z  10  z  1

c  c

, z  1

z 

 2mv

 22km

86 CHAPTER 3 Single Degree-of-Freedom Systems

In the absence of forcing, that is, when , the motion of a vibra-

tory system expressed in terms of nondimensional quantities can be described

by just one system parameter. This fact is further elucidated in Section 4.2,

where free oscillations are considered and it is shown that the qualitative nature

of these oscillations can be completely characterized by the damping factor. In

the presence of forcing, that is, , both the damping factor z and the

natural frequency v

are important for characterizing the nature of the re-

sponse. This is further addressed when the forced responses of single degree-

of-freedom systems are considered in Chapters 5 and 6.

Since the damping coefﬁcient is one of the most important descriptors of

a vibratory system, it is important to understand its interrelationships with the

component’s parameters m (or J), c (or c

), and k (or k

). We shall illustrate

some of these relationships with the following example.

EXAMPLE 3.7

Effect of mass on the damping factor

A system is initially designed to be critically damped—that is, with a damping

factor of . Due to a design change, the mass of the system is increased

20%—that is, from m to 1.2m. Will the system still be critically damped if the

stiffness and the damping coefﬁcient of the system are kept the same?

The deﬁnition of the damping factor is given by Eq. (3.18) and that for

the critical damping factor is given by Eq. (3.19). Then, the damping factor of

the system after the design change is given by

Therefore, the system with the increased mass is no longer critically damped;

rather, it is now underdamped.

EXAMPLE 3.8

Effects of system parameters on the damping ratio

An engineer ﬁnds that a single degree-of-freedom system with mass m, damp-

ing c, and spring constant k has too much static deﬂection d

. The engineer

would like to decrease d

by a factor of 2, while keeping the damping ratio

constant. We shall determine the different options.

Noting that this is a problem involving vertical vibrations, it is seen from

Eqs. (3.6), (3.15), and (3.18) that

(a)

From Eqs. (a), we see that there are three ways that one can achieve the goal.

2z 

 c



new



22k11.2m2

 0.91

22km

 0.91

 0.91  1  0.91

z  1

f 1t2 0

f 1t2 0

3.3 Natural Frequency and Damping Factor 87

First Choice

For the ﬁrst choice, let c remain constant. Then, when d

is reduced by

one-half,

(b)

and, therefore, the mass has to be reduced by a factor of and the stiffness

has to be increased by a factor of ; that is,

(c)

since,

(d)

Thus, for and c held constant, and .

Second Choice

For the second choice, let m remain constant. Then, when d

is reduced by

one-half,

(e)

and, therefore, the damping coefﬁcient has to be increased by a factor of

and the stiffness has to be increased by a factor of 2; that is,

(f)

since,

(g)

Thus, for and m held constant, and .

Third Choice

For the last choice, let k remain constant. Then, when d

is reduced by one-half,

(h)

Thus, the mass has to be reduced by a factor of 2; that is,

(i)m 씮



씮



c 씮 c22

k 씮 2kd

씮 d



씮



c 씮 c22

and

k 씮 2k

2z 

씮

k 씮 k22m 씮 m/ 22d

씮 d



씮

k22



m 씮

and

k 씮 k22

2z  c

씮 c

2gm

88 CHAPTER 3 Single Degree-of-Freedom Systems

Furthermore, since

(j)

the damping coefﬁcient has to be reduced by a factor of ; that is,

(k)

Thus, for and k held constant, and .

Notice that in all three cases the natural frequency increases by a factor

of . The results of this example can be generalized to a design guideline

(see Exercises 3.22 and 3.23).

In the next two sections, the governing equations for different types of

damping models and forcing conditions are presented. For all of these cases,

translational motions are considered for illustrative purposes, and the equa-

tions are obtained by carrying out a force balance along the direction of mo-

tion. The form of the governing equations will be similar for systems involv-

ing rotational motions.

3.4 GOVERNING EQUATIONS FOR DIFFERENT TYPES OF DAMPING

The governing equations of motion for systems with different types of damp-

ing are obtained by replacing the term corresponding to the force due to vis-

cous damping with the force due to either the ﬂuid, structural, or dry friction

type damping. Solutions for different periodically forced systems are given

in Section 5.8, where equivalent viscous damping coefﬁcients for different

damping models are obtained.

Coulomb or Dry Friction Damping

After using Eq. (2.52) to replace the term in Eq. (3.8), the governing equa-

tion of motion takes the form

(3.24)

which is a nonlinear equation because the damping characteristic is piece-

wise linear. This piece-wise linear property can be used to ﬁnd the solution of

this system.

Fluid Damping

After using Eq. (2.54) to replace the cx˙ term in Eq. (3.8), the governing equa-

tion takes the form

Nonlinear dry

friction force

 kx  mmgsgn 1x

2 f 1t 2

c 씮 c/ 22m 씮 m/2d

씮 d

c 씮

2z 

2km

⎫

⎬

⎭

3.5 Governing Equations for Different Types of Applied Forces 89

(3.25)

which is a nonlinear equation due to the nature of the damping.

Structural Damping

After using Eq. (2.57) to replace the cx˙ term in Eq. (3.8), we arrive at the gov-

erning equation

(3.26)

Equation (3.26) is further addressed in Section 5.8.

3.5 GOVERNING EQUATIONS FOR DIFFERENT TYPES OF APPLIED FORCES

In Section 3.2, we addressed governing equations of single degree-of-

freedom systems whose inertial elements were subjected to direct excitations.

Here, we address governing equations of single degree-of-freedom systems

subjected to base excitations, systems excited by rotating unbalance, and sys-

tems immersed in a ﬂuid.

3.5.1

System with Base Excitation

The base-excitation model is a prototype that is useful for studying buildings

subjected to earthquakes, packaging during transportation, vehicle response,

and for designing accelerometers (see Section 5.6). Here, the physical system

of interest is represented by a single degree-of-freedom system whose base is

subjected to a displacement disturbance y(t), and an equation governing the

motion of this system is sought to determine the response of the system x(t).

If the system of interest is an automobile, then the road surface on which

it is traveling can be a source of the disturbance y(t) and the vehicle response

x(t) is to be determined. To avoid failure of electronic components during trans-

portation, a base-excitation model is used to predict the vibration response of

the electronic components. For buildings located above or adjacent to subways

or above ground railroad tracks, the passage of trains can act as a source of

excitation to the base of the building. In designing accelerometers, the ac-

celerometer responses to different base excitations are studied to determine the

appropriate accelerometer system parameters, such as the damping factor.

A prototype of a single degree-of-freedom system subjected to a base ex-

citation is illustrated in Figure 3.6. The system represents an instrumentation

package being transported in a vehicle. The vehicle provides the base excita-

tion y(t) to the instrumentation package modeled as a single degree-of-

 kbpsgn1x

2x  kx  f 1t 2

Nonlinear ﬂuid

damping force

 c

x

 x

 kx  f 1t2

⎫

⎬

⎭