Balakumar Balachandran, Magrab E.B. Vibrations

Подождите немного. Документ загружается.

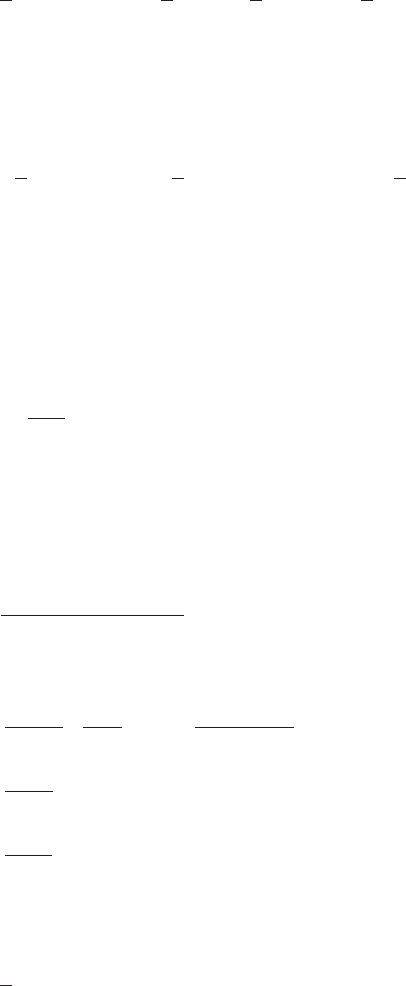
System Kinetic Energy

The total kinetic energy of the system is

(b)

where J

and J

are the mass moments of inertia of bar of mass m

and bar

of mass m

about the ﬁxed point O, respectively, and J

is the mass moment

of inertia of bar m

about the ﬁxed point O. Then, making use of Eq. (b) of

Example 2.1 and Figure 3.15, we ﬁnd that

(c)

Since the angle b and the length r(w) are each related to w by Eqs. (a), we

proceed to obtain expressions for and (w) in terms of . We differentiate

the ﬁrst of Eqs. (a) with respect to time to obtain

which leads to

(d)

Upon differentiating the third of Eqs. (a) with respect to time, we arrive at

which results in

(e)

We now use Eqs. (a) and Eq. (d) in Eq. (e) to obtain

(f)

After substituting Eqs. (d) and (f) into Eq. (b), we arrive at the following

expression for the total kinetic energy in terms of

(g)T 

m1w 2w



1w 2

3ab cos w  b



1w 2

 ab cos w  r

1w 24



b sin w

r1w2

sin w c

a  b cos w

r1w2

d b w

sin w f



1w 2 cos b  bw

sin w

r1w2 sin b

1w 2cos b  r1w2b

sin b  bw

sin w  0

1w 2

r1w 2

sin w

2r 1w2r

1w 2 2ab w

sin w



and



T 

 J



1w 2

110 CHAPTER 3 Single Degree-of-Freedom Systems

where

(h)

System Potential Energy

The system potential energy is given by

(i)

Equation of Motion

Since the expressions for kinetic energy and potential energy are not in the

standard form of Eqs. (3.46), we will make use of the Lagrange equation

given by Eq. (3.44) to obtain the equation of motion; that is,

(j)

where we have used the fact that the generalized force is zero. Noting that

there is no dissipation in the system—that is, D  0—we substitute for the

kinetic energy and potential energy from Eqs. (g) and (i), respectively, into

Eq. (j), and carry out the differentiation operations to obtain the following

nonlinear equation

(k)

where the prime denotes the derivative with respect to w.

EXAMPLE 3.17

Oscillations of a crankshaft

Consider the model of a crankshaft shown in Figure 3.16 where gravity is act-

ing in the k direction. The crank of mass m

and mass moment of inertia J

about its center of mass is connected to a slider of mass m

at one end and to

a disk of mass moment of inertia J

about the ﬁxed point O. Choosing the an-

gle u as the generalized coordinate, we will ﬁrst derive the governing equation

m1w 2w



m¿1w 2w

 kr1w 2r¿1w 2 k

w  k

ed1t 2

b



 0

V 

1w 2

3d1t2 ew4

 m

r1w 2

sin wb

m1w 2 J

 J

 1J

 m

ab cos w  b

1w 2

3.6 Lagrange’s Equations 111

G. Genta, Vibration of Structures and Machines: Practical Aspects, 2nd ed., Springer-Verlag,

NY, pp. 338–341 (1995); and E. Brusa, C. Delprete, and G. Genta, “Torsional Vibration of Crank-

shafts: Effects of Non-Constant Moments of Inertia,” J. Sound Vibration, Vol. 205, No. 2,

pp. 135–150 (1997).

of motion of the system, and then from this equation, determine the equation

governing oscillations about a steady rotation rate.

Kinematics

From Figure 3.16, we see that the position vector of the slider mass m

with

respect to point O is

(a)

and that the position vector of the center of mass G of the crank with respect

to point O is

(b)

Furthermore, from geometry, the angle g and the angle u are related by the

relation

(c)

To determine the slider velocity, we differentiate the position vector r

with respect to time and obtain

(d)

By differentiating Eq. (c) with respect to time, we obtain the following rela-

tionship between g˙ and u

(e)

After substituting Eq. (e) into Eq. (d), we obtain the slider velocity to be

(f)

The velocity of the center of mass G of the crank is obtained in a similar

manner. We differentiate Eq. (b) with respect to time to obtain

(g)v

 1ru

sin u  ag

sin g2i  1ru

cos u  ag

cos g2j

ru

1sin u  tan g cos u2i



cos u

cos g

 1ru

sin u  lg

sin g2i

r sin u  d  l sin g

 1r cos u  a cos g 2i  1r sin u  a sin g 2j

 1r cos u  l cos g 2i  dj

112 CHAPTER 3 Single Degree-of-Freedom Systems

, J

M(t)





FIGURE 3.16

Crankshaft model.

After substituting Eq. (e) into Eq. (g) and noting that a  b  l, we obtain the

velocity of the crank’s center of mass to be

(h)

System Kinetic Energy

The total kinetic energy of the system is given by

(i)

We now substitute Eqs. (e), (f), and (h) into Eq. (i) to obtain

(j)

where

(k)

and from Eq. (c)

(l)

Equation of Motion

Noting that the generalized coordinate q

 w, the system potential energy is

zero, the system dissipation function is zero, and that the generalized moment

M(t), Eq. (3.44) takes the form

(m)

Upon substituting Eq. (j) into Eq. (m) and performing the differentiation op-

erations, we obtain

(n)

where the prime denotes the derivative with respect to u.

The angle u can be expressed as the superposition of a rigid-body motion

at a constant angular velocity v and an oscillatory rotation f; that is,

(o)

Then, from Eqs. (n) and (o), we arrive at

(p)J1u 2f



J¿1u 21v  f

M1t 2

u1t 2 vt  f1t2

J1u 2u



J¿1u 2u

M1t 2

b

M1t 2

g  sin

1

sin u 

 J

cos u

cos g

 r

1sin u  tan g cos u2

J1u 2 J

 r

easin u 

tan g cos u b

 a

cos u b

T 

J1u 2u

T 



2



asin u 

tan g cos u bru

i  a

cos u bru

3.6 Lagrange’s Equations 113

EXAMPLE 3.18 Vibration of a centrifugal governor

A centrifugal governor is a device that automatically controls the speed of an

engine and prevents engines from exceeding certain speeds or prevents dam-

age from sudden changes in torque loading. We shall derive the equation of

motion of such a governor by using Lagrange’s equation. A model of this de-

vice is shown in Figure 3.17.

The velocity vector relative to point o of the left hand mass is given by

(a)

From Eq. (1.22) and Eq. (a), the kinetic energy is

(b)

 mv

1r  L sin w2

 mw

 m c1Lw

cos w2

 1Lw

sin w2

 11r  L sin w2v2

T 1w, w

2 2 c

m1V

Lw

cos wi  Lw

sin w j  1r  L sin w2vk

114 CHAPTER 3 Single Degree-of-Freedom Systems

J. P. Den Hartog, Mechanical Vibrations, Dover, p. 309, 1985; and Z.-M. Ge and C.-I Lee,

“Nonlinear Dynamics and Control of Chaos for a Rotational Machine with a Hexagonal

Centrifugal Governor with a Spring,” J. Sound Vibration, 262, pp. 845–864, 2003.

Controlled arm

(rLsin)

[⊥ to page]





Lϕ

FIGURE 3.17

Centrifugal governor.

The potential energy with respect to the static equilibrium position is

(c)

where the factor of 2 inside the parenthesis is because each pair of linkages

compresses the spring from both the top and the bottom.

Upon using Eq. (3.44) with q

 w, noting that , and

performing the required operations, we obtain the following governing

equation

(d)

Introducing the quantities

(e)

Eq. (d) is rewritten as

(f)

If we assume that the oscillations w about w  0 are small, then

, and Eq. (f) simpliﬁes to

(g)

From the stiffness coefﬁcient in the equation of motion, we see that for

the stiffness coefﬁcient is negative.

EXAMPLE 3.19

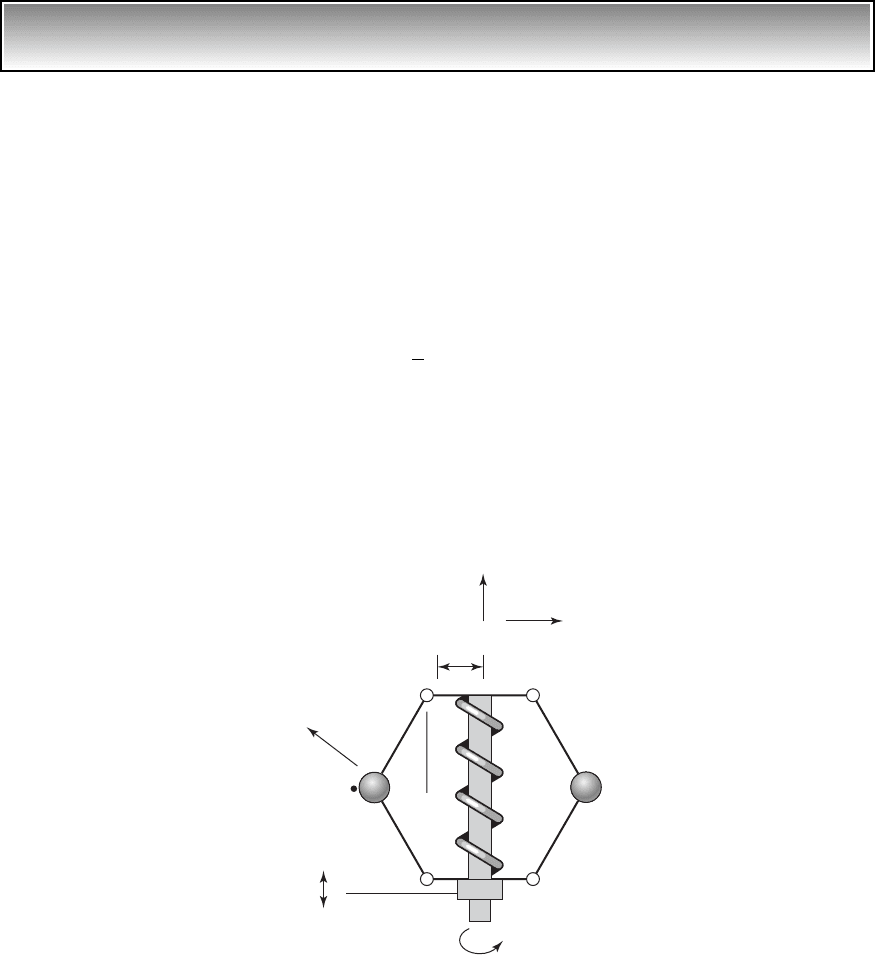
Oscillations of a rotating system

A cylindrical wheel is placed on a platform that is rotating about its axis with

an angular speed . The center of the wheel is attached to the platform by a

spring with constant k, as shown in Figure 3.18. We shall determine the

change in the equilibrium position of the wheel and the natural frequency of

the system about this equilibrium position. When , the center of the

wheel is at a distance R from the axis of rotation, which is the length of the

unstretched spring.

If we denote the change in the equilibrium of the spring due to the rota-

tion , then at equilibrium, the spring force is equal to the centrifugal

force, which can be represented as

kd  m1R  d2Æ

Æ as d

Æ  0

v  v

 1v

 v

2w  gv

sin w  wcos w  1,

 gv

cos w  1v

 v

2sin w cos w  1v

 v

2sin w  0

g 



and



 L 1mg  2kL2sin w  0

 mrLv

cos w  1mv

 2k2L

sin w cos w

 D  0

V1w 2

k 12L 11  cos w22

 2mgL cos w

3.6 Lagrange’s Equations 115

116 CHAPTER 3 Single Degree-of-Freedom Systems

Upon solving for , we obtain

where

For small angles of rotation, the kinetic energy is

The potential energy for oscillations about the equilibrium position is

The Lagrange equation for this undamped system is

where the centrifugal force is treated as an external force. Thus, the

governing equation is

Hence, from the stiffness and inertia terms in the governing equations of mo-

tion, the natural frequency is

rad/s

3.7 SUMMARY

In this chapter, the use of two different methods to derive the governing equa-

tion of motion of a single degree-of-freedom system was illustrated. One of

these methods is based on applying force and/or moment balance and the

other method is based on Lagrange’s equations. The underlying approach for

each of these methods will be used again for deriving governing equations of

systems with multiple degrees of freedom in Chapter 7. Deﬁnitions of natu-

ral frequency and damping factor were also introduced. It was shown how the

static-equilibrium position of a vibratory system can be determined and how

nonlinear systems can be linearized to describe small oscillations about a sys-

tem’s equilibrium position.



 Æ

m bx

 1k  mÆ

2x  0

mxÆ

b



 Q

 mxÆ

V 

T 





m bx



d 

/Æ

 1

Ω

FIGURE 3.18

Elastically restrained wheel on

a rotating platform.

Exercises 117

a that is rotating about its axis at a speed of rad/s.

Assume that the mass of the beam is negligible and its

equivalent stiffness is k

. Derive the governing equa-

tion of motion for transverse vibrations of the beam in

terms of the variable x.

Section 3.2.2

3.6 Derive the governing equation of motion for the

rocker-arm valve assembly shown in Figure E3.6. As-

sume “small” motions. The quantity J

is the mass

moment of inertia about point O of the rocker arm of

length (a  b), k is the stiffness of the linear spring

that is ﬁxed at one end, and M is the external moment

imposed by the cam on the system. This moment is

produced by the contact force generated by the cam at

one end of the rocker arm.

3.7 Derive the governing equation of motion for the

system shown in Figure E3.7. The mass moment of

EXERCISES

Section 3.2.1

3.1 Rewrite the second-order system given by Eq.

(3.8) as a system of two ﬁrst-order differential equa-

tions by introducing the new variables and

. The resulting system of equations is said to be

in state-space form, a useful form for numerically de-

termining the solutions of vibrating systems.

3.2 A vibratory system with a hardening nonlinear

spring is governed by the following equation

Determine the static-equilibrium position of this sys-

tem for a  1 and linearize the system for “small” os-

cillations about the system static-equilibrium position.

3.3 A vibratory system with a softening nonlinear

spring is governed by the following equation

Determine the static-equilibrium positions of this sys-

tem for a  1 and linearize the system for “small” os-

cillations about each of the system static-equilibrium

positions.

3.4 Determine the equation governing the system stud-

ied in Example 3.13 by carrying out a force balance.

3.5 A mass m is attached to the free end of a thin can-

tilever beam of length L, as shown in Figure E3.5. The

ﬁxed end of this beam is attached to a shaft of radius

 cx

 k1x  ax

2 0

 cx

 k1x  ax

2 0

 x

FIGURE E3.5

m x



FIGURE E3.6

FIGURE E3.7

c.g.



L/2

118 CHAPTER 3 Single Degree-of-Freedom Systems

mine the equation of motion of this system, and from

this governing equation, ﬁnd the natural frequency

and damping factor of the system.

3.15 A spring elongates 2.5 mm when stretched by a

force of 5 N. Determine the static deﬂection and the

period of vibration if a mass of 8 kg is attached to the

spring.

3.16 Determine the natural frequency of the steel disk

with torsion spring shown in Figure E3.16 when

, d  50 mm, r

disk

 7850 kg/m

and h  2 mm.

 0.488 N

m/rad

inertia of the bar about the point O is J

, and the tor-

sion stiffness of the spring attached to the pivot point

is k

. Assume that there is gravity loading.

3.8 Determine the equation governing the system stud-

ied in Example 3.15 by carrying out a force balance.

Section 3.3.1

3.9 A cylindrical buoy with a radius of 1.5 m and a

mass of 1000 kg ﬂoats in salt water (r  1026 kg/m

Determine the natural frequency of this system.

3.10 A 10 kg instrument is to be mounted at the end of

a cantilever arm of annular cross section. The arm has

a Young's modulus of elasticity E  72  10

N/m

and a mass density r  2800 kg/m

. If this arm is

500 mm long, determine the cross-section dimensions

of the arm so that the ﬁrst natural frequency of the

system is above 50 Hz.

3.11 The static displacement of a system with a motor

weight of 385.6 kg is found to be 0.0254 mm. Deter-

mine the natural frequency of vertical vibrations of

this system.

3.12 A rotor is attached to one end of a shaft that is ﬁxed

at the other end. Let the rotary inertia of the rotor be J

and assume that the rotary inertia of the shaft is negli-

gible compared to that of the rotor. The shaft has a di-

ameter d, a length L, and it is made from material with

a shear modulus G. Determine an expression for the

natural frequency of torsional oscillations.

3.13 Obtain an expression for the natural frequency

for the system shown in Figure E3.5.

3.14 Consider the hand motion discussed in Example

3.3 and let the hand move in the horizontal plane; that

is, the gravity force acts normal to this plane. Assume

that the length of the forearm l is 25 cm, the mass

of the fore arm m is 1.5 kg, the object being carried

in the hand has a mass M  5 kg, the constant k

as-

sociated with the restoring force of the biceps is 2 

N/rad, the constant K

associated with the triceps

is 2  10

N/rad, and the spacing a  4 cm. Deter-

3.17 Consider a nonlinear spring that is governed by

the force-displacement relationship

where a  3000 N, b  0.015 m, and c  2.80. If this

spring is to be used as a mounting for different

machinery systems, obtain a graph similar to that

shown in Figure 3.5b and discuss how the natural

frequency of this system changes with the weight of

the machinery.

3.18 The static deﬂection in the tibia bone of a 120 kg

person standing upright is found to be 25 m.

Determine the associated natural frequency of axial

vibrations.

3.19 A solid wooden cylinder of radius r, height h, and

speciﬁc gravity s

is placed in a container of tap wa-

ter such that the axis of the cylinder is perpendicular

to the surface of the water. Assume that the density of

F1x 2 a a

FIGURE E3.16

Exercises 119

Section 3.3.2

3.22 Formulate a design guideline for Example 3.8

that would enable a vibratory system designer to de-

crease the static deﬂection by a factor n while holding

the damping ratio and damping coefﬁcient constant.

3.23 Formulate a design guideline for Example 3.8

that would enable a vibratory system designer to de-

crease the static deﬂection by a factor n while keeping

the damping ratio and mass m constant.

3.24 An instrument's needle indicator has a rotary in-

ertia of . It is attached to a torsion

spring whose stiffness is and a

viscous damper of coefﬁcient c. What is the value of c

needed so that the needle is critically damped?

3.25 Determine the natural frequency and damping

factor for the system shown in Figure E2.26.

3.26 Determine the natural frequency and damping

factor for the system shown in Figure E2.27.

Section 3.6

3.27 For the base-excitation prototype shown in Fig-

ure 3.6, assume that the base displacement y(t) is

known, choose x(t) as the generalized coordinate, and

derive the equation of motion by using Lagrange's

equation.

3.28 Obtain the equation of motion for the system

with rotating unbalance shown in Figure 3.7 by using

Lagrange's equations.

3.29 Obtain the equation of motion for the system

shown in Figure 3.10 by using moment balance and

compare it to the results obtained by using Lagrange's

equation.

3.30 Derive the governing equation for the single-

degree-of-freedom system shown in Figure E3.30 in

terms of u when u is small, and obtain an expression

for its natural frequency. The top mass of the pendu-

lum is a sphere, and the mass m

of the horizontal rod

and the mass m

of the rod that is supporting m

are

1.1  10

5

m/rad

1.4  10

the water is . It is assumed the wooden cylinder

stays upright under small oscillations.

a) If the cylinder is displaced a small amount, then

determine an expression for its natural frequency.

b) If the tap water is replaced by salt water with spe-

ciﬁc gravity of 1.2, then determine whether the

natural frequency of the wooden cylinder in-

creases or decreases and by what percentage.

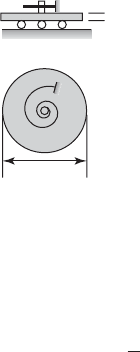
3.20 Consider the pulley system shown in Figure

E3.20. The mass of each pulley is small compared

with the mass m and, therefore, can be ignored. Fur-

thermore, the cord holding the mass is inextensible

and has negligible mass. Obtain an expression for the

natural frequency of the system.

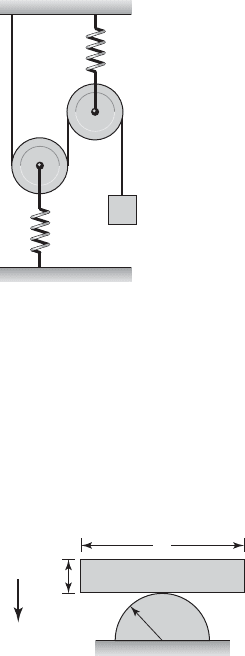
3.21 A rectangular block of mass m rests on a station-

ary half-cylinder, as shown in Figure E3.21. Find the

natural frequency of the block when it undergoes

small oscillations about the point of contact with the

cylinder.

FIGURE E3.21

FIGURE E3.20