Balakumar Balachandran, Magrab E.B. Vibrations

Подождите немного. Документ загружается.

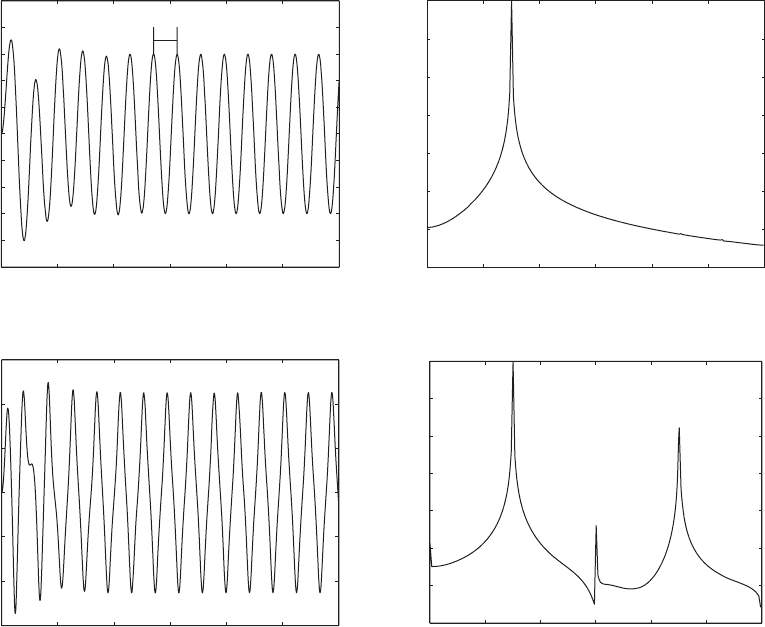
The solution to Eq. (5.162) has to be obtained numerically

for the non-

linear case (a  0). For the linear and nonlinear cases, we assume that 



3, z  0.4, and F

/k  50 units; for the nonlinear case, we assume that a 

1.5. The numerical solutions to Eq. (5.162) are presented in Figure 5.47,

along with their amplitude spectra. The amplitude spectra were obtained from

the steady-state portions of the signal;

that is, for v

t  10. We see that in

270 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations

The MATLAB function ode45 was used.

The MATLAB function fft was used.

(a) (b)

0 5 10 15 20 25 30

10

8

6

4

2

2p/Ω

0 2 4 6 8 10 12

70

60

50

40

30

20

10

Ω

0 5 10 15 20 25 30

6

4

2

x(t)

0 2 4 6 8 10 12

70

60

50

40

30

20

10

Ω

 3

3Ω

 9

Time domain Frequency domain

FIGURE 5.47

Displacement response of linear (z  0.4) and nonlinear (z  0.4 and a  1.5) systems to harmonic excitation: (a) time history

of linear system; (b) amplitude spectrum of linear system; (c) time history of nonlinear system; and (d) amplitude spectrum of

nonlinear system.

the time domain, the steady-state nonlinear response is not sinusoidal. From

an examination of the amplitude response, we see that it is the sum of two

components; that at the driving frequency 

 3 and one additional one at

the third harmonic, 3

 9. The third harmonic is due to the nonlinear be-

havior of the spring.

For weak nonlinearity, the following approximation for the periodic am-

plitude response of the nonlinear system has been obtained

from a two-term

approximate solution to Eq. (5.162)

(5.163)

where v/v

and

(5.164)

In Eqs. (5.163) and (5.164), X is the nondimensional magnitude of the dis-

placement of the mass, X

is the nondimensional response amplitude, and S is

the nondimensional force amplitude. In Eq. (5.163), the plus sign is used for a

hardening spring (a  0) and the minus sign is used for a softening spring

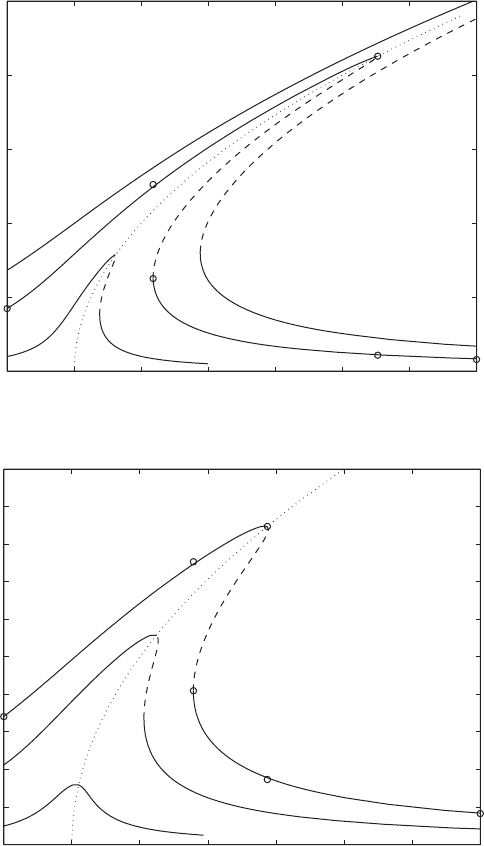
(a  0). A graph of Eq. (5.163) is given in Figure 5.48.

Unlike the case of a

linear system, the maximum value of the amplitude occurs at an excitation fre-

quency away from the natural frequency. This type of result also appears in the

design of strain gauges.

In Figure 5.48, the amplitude information is pre-

sented along with information about the stability of the response.

In Figure 5.48, the solid lines are used to represent the loci of stable pe-

riodic responses and the broken lines are used to represent the loci of unsta-

ble responses. The determination of stability of periodic responses is not dis-

cussed here, but broadly speaking, an unstable periodic response is not stable

to disturbances.

To examine what happens along a frequency-response curve, let us look

at the curve plotted for z  0.05 and S  0.5. In this case, as the excitation

frequency is increased gradually from 0, the response amplitude follows the

branch EDA. At the excitation frequency corresponding to point A, a jump oc-

curs, and for further increases in the excitation frequency, the response fol-

lows the branch BF. On the reverse sweep, as the excitation frequency is de-

creased from the value corresponding to the point F, the response follows the

branch FBC before a jump takes place at point C. For further decrease in the

excitation frequency, the response follows the branch DE.

 X

and

S 

k B



211  X



 12z2

5.10 Inﬂuence of Nonlinear Stiffness on Forced Response 271

See, for example, L. S. Jacobsen and R. B. Ayre, Engineering Vibrations, McGraw-Hill, NY,

pp. 286–293 (1958); or A. H. Nayfeh and D. T. Mook, Nonlinear Oscillations, John Wiley &

Sons, NY (1979).

For a  0, the curves would “bend” in the other direction.

C. Gui et al., “Nonlinearity and Hysteresis of Resonant Strain Gauges,” J. Microelectro-

mechanical Systems, Vol. 7, No. 1, pp. 122–127 (March 1998).

A. H. Nayfeh and B. Balachandran, Applied Nonlinear Dynamics: Analytical, Computational,

and Experimental Methods, John Wiley & Sons, NY, Chapter 2 (1995).

(a)

(b)

0 1 2 3 4 5 6 7

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

S  0

Ω

S  0.1

S  0.5

S  1

0 1 2 3 4 5 6 7

0.5

1.5

2.5

S  0

Ω

S  0.1

S  0.5

S  1

FIGURE 5.48

Representative amplitude response for system with linear and nonlinear stiffness elements

with a  0: (a) z  0.05 and (b) z  0.15.

The locus of the peak amplitudes shown by a dotted line in Figure 5.48

is called a backbone curve. It is given by

(5.165)

When the nonlinearity is of the softening type, the frequency curves bend to-

ward the left as the excitation amplitude is increased. Again, jumps occur in

the response, beyond certain excitation amplitudes. Also, in some cases,

chaotic motions, which are a form of aperiodic motions with identiﬁable char-

acteristics, can be obtained.

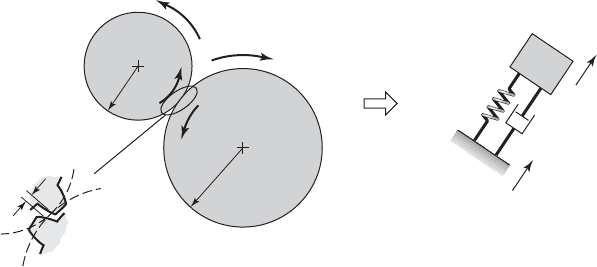
Case 2: Dynamic interactions of gear teeth

We shall derive the governing equation of motion for a pair of meshing gears

that incorporates nonlinear stiffness characteristics, which arise in real sys-

tems due to the changing gear teeth contact regimes and the tooth separations

due to tooth clearances (backlash). This governing equation is numerically

solved to study the nonlinear behavior of the system.

The simpliﬁed gear system is shown in Figure 5.49a, where the gear cen-

ters are rigidly mounted and the stiffness and damping are provided by the

elasticity and damping of the meshing gear teeth. The equivalent single

degree-of-freedom system is shown in Figure 5.49b, where x

is the tangential



 1  X

5.10 Inﬂuence of Nonlinear Stiffness on Forced Response 273

A. H. Nayfeh and B. Balachandran, ibid.

For a more complete treatment of gear systems see, for example: A. Kahraman and R. Singh,

“Interactions between time-varying mesh stiffness and clearance non-linearities in a geared sys-

tem,” J. Sound Vibration, Vol. 146, No. 1, pp. 135–156 (1991); A. Kahraman and G. W. Blanken-

ship, “Interactions between commensurate parametric and forcing excitations in a system with

clearance,” J. Sound Vibration, Vol. 194, No. 3, pp. 317–336 (1996); C. Padmanabhan and

R. Singh, “ Analysis of periodically forced nonlinear Hill’s oscillator with application to a geared

system,” J. Acoustic Soc. Amer., Vol. 99, No. 1, pp. 324–334 (January 1996); and S. Theodossi-

ades and S. Natsiavas, “Non-linear dynamics of gear-pair systems with periodic stiffness and

backlash,” J. Sound Vibration, Vol. 229, No. 2, pp. 287–310 (2000).

k(t)

(b)(a)



Pinion

FIGURE 5.49

(a) Meshing gears and (b) equivalent single degree-of-freedom system model.

displacement of a meshing tooth on gear 1 and x

is the tangential displace-

ment of the meshing tooth on gear 2. These quantities are related to the rota-

tions by

 r

j  1, 2 (5.166)

where r

is the radius of gear j and w

is the angular rotation of gear j. The ro-

tation w

is assumed to consist of a steady-state mesh speed v

, where v

and

are rotational speeds of gears 1 and 2, respectively, and a variation about

this steady-state value given by u

(t); that is,

(t)  v

t  u

(t) j  1, 2 (5.167)

Thus, Eqs. (5.166) become

 r

t  u

(t)) j  1, 2 (5.168)

Governing Equation of Motion

The meshing gear teeth are modeled as a single degree-of-freedom system

with a moving base as shown in Figure 5.49b, where the quantity m

is deter-

mined as follows. Since we have a system with a moving base, we form the

difference between the displacements of gears 1 and 2 as

z  x

 x

 r

 r

(5.169)

where we have used Eq. (5.168) and noted that r

 r

. Next, we differ-

entiate Eq. (5.169) twice with respect to time to obtain

(5.170)

However, from Figure 5.49a and Eqs. (1.17) and (1.21), we have that

(5.171)

where T

is the variation of the torque and F is the corresponding force. From

Eqs. (5.170) and (5.171), we obtain

(5.172)

or, equivalently, as

(5.173)

where the effective inertia m

is given by

(5.174)

We assume that the stiffness of the gear tooth is the time-varying function

k(t)  k

(1  P cos v

t) (5.175)

 a



1

F  m



F 

F  a



J

 r

 J

 r

 r

274 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations

where k

is the mean stiffness, P is a stiffness ratio, and v

 n

the rotating speed of the gears and n

and n

are the number of teeth on gears

1 and 2, respectively. The stiffness of the gear tooth is only engaged when the

mating teeth come in contact; that is, after the mating tooth traverses a small

separation distance b. This is similar, in principle, to the nonlinear spring sys-

tem shown in Figure 4.24. Hence, we use the following relation to express the

restoring force of the spring

 k(t)h(z) (5.176)

where

(5.177)

The governing equation for the system shown in Figure 5.49 is, therefore,

(5.178)

where we assume that the applied force on the teeth of the pinion is

(5.179)

and T

is the steady-state torque applied by the pinion and a is a parameter used

to select the magnitude of the time-varying portion of the torque. To convert

Eq. (5.178) to a nondimensional form, we introduce the following deﬁnitions

(5.180)

Then, Eq. (5.178) becomes

(5.181)

where the overdot indicates the derivative with respect to t and

(5.182)

Numerical Results

The steady-state responses of the numerical evaluation

of Eq. (5.181) are

shown in Figure 5.50. It is seen that for P  0 the steady-state time histories

exhibit a harmonic response. As the magnitude of P increases, the steady-state

response is transformed into a nonharmonic periodic solution with an in-

creasing peak-to-peak value.

 p  sgn1p2

0p 0 1

h1p 2 0 0p 0 1

 2zp

 11  P cos 

t2h1p 2 f

11  a cos 

t  v



p 



2z 





f 1t 2

11  a cos v

 cz

 k1t 2h1z2 f 1t 2

 z  b sgn1z2

0z 0 b

h1z 2 0 0z 0 b

5.10 Inﬂuence of Nonlinear Stiffness on Forced Response 275

The MATLAB function ode45 was used.

EXAMPLE 5.20 Determination of system linearity from amplitude

response characteristics

Suppose that you are told that you have a single degree-of-freedom system

subjected to periodically varying excitation with a known magnitude A

. An

engineer gives you a spectrum of the displacement of the mass, which is

shown in Figure 5.51. The engineer wants to know what could cause the spec-

trum to look like this and if there is a way to determine the cause if there is

more than one way that this could have occurred.

276 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations

(a) (b)

170 180 190 200 210 220 230 240 250

1.07

1.08

1.09

1.1

1.11

1.12

1.13

1.14

p(t)

170 180 190 200 210 220 230 240 250

1.092

1.094

1.096

1.098

1.1

1.102

1.104

1.106

1.108

1.11

p(t)

170 180 190 200 210 220 230 240 250

1.04

1.06

1.08

1.1

1.12

1.14

1.16

1.18

1.2

p(t)

170 180 190 200 210 220 230 240 250

0.95

1.05

1.1

1.15

1.2

1.25

p(t)

FIGURE 5.50

Steady-state time histories of gear system for 

 0.5, z  0.05, a  0.05, f

 0.1: (a) P  0; (b) P  0.1; (c) P  0.2;

and (d) P  0.4.

There are two possible scenarios in which this type of spectrum can

occur. In one scenario, the excitation force is composed of two frequency

components, one at v

and the other at 3v

and the system has a linear stiff-

ness. The other scenario is one where the system is subjected to a force at fre-

quency v

and the system has a nonlinear cubic spring, such as the one de-

scribed in this section. Both of these scenarios can produce this spectrum.

There are two independent ways to determine which of these scenarios

is applicable here. One can subject the system’s spring to a series of known

static forces, which includes as one of its values the forcing amplitude A

, and

measure the corresponding displacements. A plot of the force levels versus

the observed displacement magnitudes would reveal whether or not the spring

is linear or nonlinear. (Recall Figures 2.8 and 2.13.) If the system is linear,

then assuming that the inertia and damping elements are linear, the forcing ex-

citation contains two frequency components.

Another approach to examine if the second scenario is present is to sub-

ject the mass to a periodic force at frequency v

only. If the spectrum of the

displacement has only one frequency component, the system is linear,

whereas if it contains two components, the system is nonlinear.

5.11 SUMMARY

In this chapter, responses of single degree-of-freedom systems subjected to

harmonic and other periodic excitations are studied. Different sources of forc-

ing such as rotating unbalance and base excitation are considered. The no-

tions of system resonance and frequency-response functions are also intro-

duced and explained. The topic of vibration isolation is discussed at length.

The underlying principles of an electrodynamic shaker and an accelerometer

are also explained. For the different damping models, the notion of an equiv-

alent viscous damping is introduced and explained. Free-displacement curves

for linear and nonlinear damping models are examined in the context of en-

ergy dissipation.

Exercises 277

⏐

X()

⏐



3



FIGURE 5.51

Spectrum of the output of single

degree-of-freedom system with

unknown properties.

EXERCISES

Section 5.2.1

5.1 A vibratory system with a natural frequency of

10 Hz is suddenly excited by a harmonic excitation at

6 Hz. What should the damping factor of the system

be so that the system settles down to within 5% of the

steady-state amplitude in 200 ms?

Section 5.2.2

5.2 A 150 kg mass is suspended by a spring-damper

combination with a stiffness of 30  10

N/m and

a viscous-damping constant of 1500 N s/m. The

mass is initially at rest. Calculate the steady-state

displacement amplitude and phase if the mass is

excited by a harmonic force amplitude of 70 N

at 3 Hz.

5.3 The dynamic ampliﬁcation or attenuation of a

single degree-of-freedom system is deﬁned as the ra-

tio of the steady-state magnitude of the displacement

response to its static displacement F

/k, where the

mass is being driven by a harmonic force of magni-

tude F

. Find the dynamic ampliﬁcation or attenua-

tion of a single degree-of-freedom system that is

being excited at 100 rad/s and has the following sys-

tem parameters: m  100 kg, k  20 kN/m, and c 

6000 N s/m.

5.4 Consider the two independent single degree-

of-freedom systems in Figure E5.4 that are each

being forced to vibrate harmonically at the same fre-

quency v. The excitation on System 1 starts at t  0,

and the excitation on System 2 starts at t  t

; that is,

a) Use Eqs. (5.1) to (5.9) to show that the steady-state

responses of the two systems are

where andv/v

, v

 v

, g  z

 u1/v

, gz

2ss

1t 2

H1/v

, gz

2 sin1/v

1t  t

1ss

1t 2

H1, z

2sin 1t  u1, z

1t 2 F

sin1v 3t  t

42u1t  t

1t 2 F

sin1vt 2u1t2

b) If both systems are operating in their respective

mass-dominated regions, then what is the ratio of

the magnitudes of the amplitudes of System 2 to

that of System 1 and their relative phase.

Section 5.2.4

5.5 The control tab of an airplane elevator is shown

schematically in the Figure E5.5. The mass moment

of inertia J

of the control tab about the hinge point O

is known, but the torsional spring constant k

associ-

ated with the control linkage is difﬁcult to evaluate,

and hence, the natural frequency is

difﬁcult to determine. An experiment is designed to

determine this natural frequency of the system. In this

experiment, the elevator is rigidly mounted, springs

with stiffness k

and stiffness k

are attached to the

control tab, and the tab is harmonically excited at an

amplitude e, as illustrated in the ﬁgure. The excitation

frequency v is varied until resonance occurs at v 

, and this value is noted. Assuming that the damping

in the system is negligible, determine an expression

for v

in terms of v

, k

, J

, and L.

 1k

u1a, b 2 tan

1

2ba

1  a

H1a, b 2

211  a

 12ba2

278 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations

(t) f

(t)

FIGURE E5.4



Control tab

e sin t

FIGURE E5.5

Exercises 279

5.6

Consider translational motions of a vibratory

system with a mass m of 200 kg and a stiffness k

of 200 N/m. When a harmonic forcing of the form

sin(vt) is suddenly applied to the mass of the sys-

tem, where F

 1.0 N, determine the responses of the

system and plot them for the following cases: (a) v 

0.2 rad/s, (b) v  1.0 rad/s, and (c) v  2.0 rad/s, and

discuss the results.

Section 5.3.3

5.7 A micromechanical resonator is to be designed

to have a Q factor of 1000 and a natural frequency of

2 kHz. Determine the system-damping factor and the

system bandwidth.

5.8 If a sensor modeled as a mass-spring-damper sys-

tem is to be redesigned so that its sensitivity is in-

creased by a factor of four, determine the correspon-

ding percentage changes in the system natural

frequency and damping ratio.

Section 5.3.4

5.9 Consider the machine of 25 kg mass that is

mounted on springs and dampers as shown in Figure

E5.9. The equivalent stiffness of the spring combina-

tion is 9 kN/m, and the equivalent damping of the

damper combination is 150 N s/m. An excitation

force F(t) is directly applied to the mass of the system,

as shown in the ﬁgure. Consider the displacement x(t)

as the output, the forcing F(t) as the input, and deter-

mine the frequency response of this system.

Section 5.4

5.10 An air compressor with a total mass of 100 kg is

operated at a constant speed of 2000 rpm. The unbal-

anced mass is 4 kg and the eccentricity is 0.12 m. The

properties of the mounting are such that the damping

factor z = 0.15. Determine the following: (a) the

spring stiffness that the mounting should have so that

only 20% of the unbalance force is transmitted to the

foundation and (b) determine the amplitude of the

transmitted force.

5.11 A motor of mass m is mounted at the end of a can-

tilever beam and it is found that the beam deﬂects

10 mm. When the motor is running at 1800 rpm, an

unbalanced force of 100 N is measured. If the beam

damping is negligible and its mass can be neglected,

then what speed should the motor operate at so that the

amplitude of the dynamic response is less than a

Section 5.5

5.12 In the system shown in Figure E5.12, y(t) is the

base displacement and x(t) is the displacement

F(t)

x(t)

FIGURE E5.9

x(t)

y(t)

c2c

Base

FIGURE E5.12