Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.

Time Domain and Frequency Domain Counterparts
We now examine the information corresponding to the displacement response
given by Eq. (6.4a) in the frequency domain. To this end, we recall the fol-
lowing Fourier transform pair given by Eq. (5.60):
(6.13)
where
(6.14)
The amplitude response H(v/v
n
) and the phase response u(v/v
n
) are given
by Eqs. (5.56a) and (5.56b), respectively, and G( jv) is the frequency-
response function given by Eq. (5.55). Hence, based on Eqs. (6.13), the
Fourier transform of the impulse response given by Eq. (6.4a) is
(6.15a)
f
o
e
zv
n
t
mv
d
sin1v
d
t2u1t 23
f
o
k
H1v/v
n
2e
ju1v/v
n
2
f
o
G1jv2
mG1jv 2
1
v
n
2
H1v/v
n
2e
ju1v/v
n
2
1
1zv
n
jv2
2
v
d
2
1
v
n
2
31 1v/v
n
2
2
2jz1v/v
n
24
e
zv
n
t
v
d
sin1v
d
t2u1t 23
1
1zv
n
jv2
2
v
d
2
290 CHAPTER 6 Single Degree-of-Freedom Systems Subjected to Transient Excitations
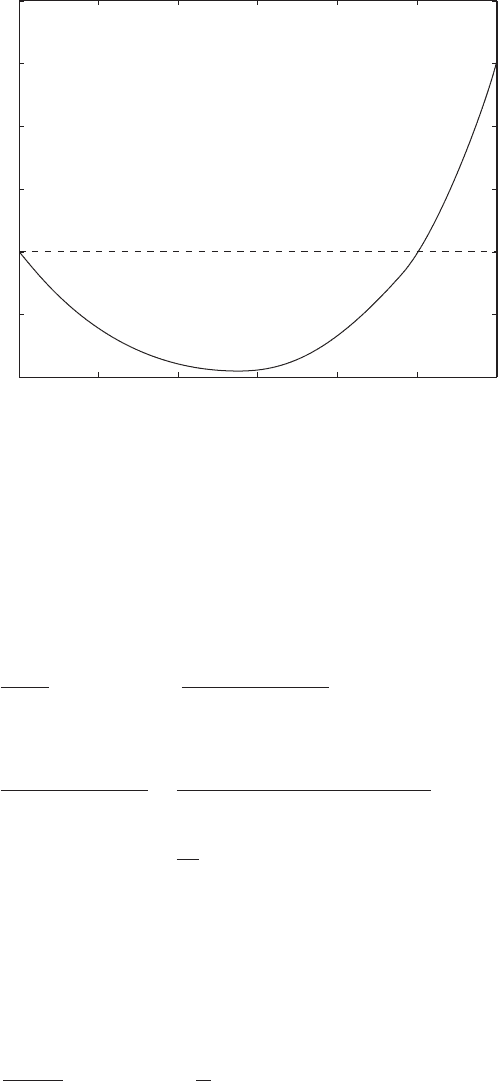
0 0.1 0.2 0.3 0.4 0.5 0.6
0.8
0.9
1
1.1
1.2
1.3
1.4
z
F
b,max
/(f
o
v
n
)
FIGURE 6.3
Maximum magnitude of impulse force transmitted to fixed boundary.

When the magnitude of the impulse f
o
is unity, a unit impulse is said to be ap-
plied to the system shown in Figure 6.1. The corresponding response is called
the impulse response of the single degree-of-freedom system and is given by
(6.15b)
This response is the time domain counterpart of its frequency-response func-
tion, which comprises the amplitude response H(v/v
n
) and the phase re-
sponse u(v/v
n
); that is,
(6.15c)
Transfer Function and Frequency-Response Function
When the initial conditions are zero, the Laplace transform of the response
given by Eq. (D.2) reduces to
(6.16)
which is rewritten as
(6.17)
where the transfer function G(s) is given by
(6.18)
In the frequency domain, Eq. (6.17) becomes
(6.19)
When an excitation of the form given by Eq. (6.2) is applied to a system, the
corresponding Laplace transform is given by transform pair 5 in Table A of
Appendix A. Thus,
(6.20)
Hence, the corresponding Fourier transform F( jv) has a constant magnitude
f
o
over the entire frequency span. In other words, the magnitude of the ampli-
tude spectrum of an impulse function is constant over the frequency range
.
From a practical standpoint, an impulse function is hard to realize, since
an ideal impulse has an “extremely large” magnitude that lasts an infinitesi-
mally short time. However, a device called an impact hammer can be used in
an experiment to apply a pulse of finite time duration to the mass of a system.
An impact hammer usually has a built-in transducer to measure the force
amplitude-time profile created by the hammer. The corresponding Fourier
transform of the hammer’s pulse has a fairly constant magnitude over a finite
0 v q
F1s 2 f
o
X1jv2 G1jv2F1jv 2
G1s 2
1
mD1s 2
X1s 2 G1s 2F1s2
X1s 2
F1s 2
mD1s 2
e
zv
n
t
mv
d
sin1v
d
t2u1t 23
1
k
H1v/v
n
2e
ju1v/v
n
2
G1jv2
h1t 2
e
zv
n
t
mv
d
sin1v
d
t2u1t 2
6.2 Response to Impulse Excitation 291

frequency bandwidth. As discussed in Section 6.6, this bandwidth becomes
larger as the pulse duration is reduced.
The notion of an impulse response leads to an experimental procedure to
determine the frequency-response function. This procedure is an alternative
to that discussed in Chapter 5 where a harmonic excitation was used to con-
struct this function. Thus, one would use an impact hammer or another source
to apply a force (or a moment) of very short time duration to the inertia
element of a system, measure and digitize the forcing and displacement re-
sponse signals, use the discrete Fourier transform on these signals to convert
the time domain information to the frequency domain, and then determine the
frequency-response function G( jv) based on Eq. (5.59c), which is appears in
this chapter as Eq. (6.19).
Response of a Linear System to Arbitrary Inputs Based on
Impulse Response
Examining Eq. (6.17), which is in the Laplace domain, one can state that for
a linear vibratory system the displacement response is the product of the sys-
tem’s transfer function and the Laplace transform of the system input. Simi-
larly, from Eq. (6.19), which is in the frequency domain, it can be stated that
the displacement response is the product of the system’s frequency-response
function and the Fourier transform of the system input. This input-output re-
lationship, which is characteristic of all linear vibratory systems, is schemat-
ically illustrated in Figure 6.4.
From the transform pair 4 in Table A of Appendix A, we arrive at the time
domain counterpart of Eq. (6.17); that is,
(6.21)x 1t 2
t
0
h1h2f 1t h2dh
292 CHAPTER 6 Single Degree-of-Freedom Systems Subjected to Transient Excitations
F(zj) X( j) 5 F( j)G( j)
f(t)
Laplace domain
Time domain
Frequency domain
X(s) 5 F(s)G(s)
F(s)
G(s)
G(s): Transfer function
G( j): Frequency-response
function
x(t) 5 h()f(t 2 )d
∫
t
0
h(t) 5 e
–
n
t
sin(
d
t)
1
m
d
h(t): Impulse response
G( j)
FIGURE 6.4
System input-output relationships in time and transformed domains.
where f (t) is the forcing applied to the inertia elements and the function h(t)
is the impulse response of the system; that is,
(6.22)
As noted in Appendix D for Eq. (D.11), Eq. (6.21) is the convolution integral.
Thus, the applied forcing is convolved with the system impulse response
function over the time interval of interest to determine the system response as a
function of time.
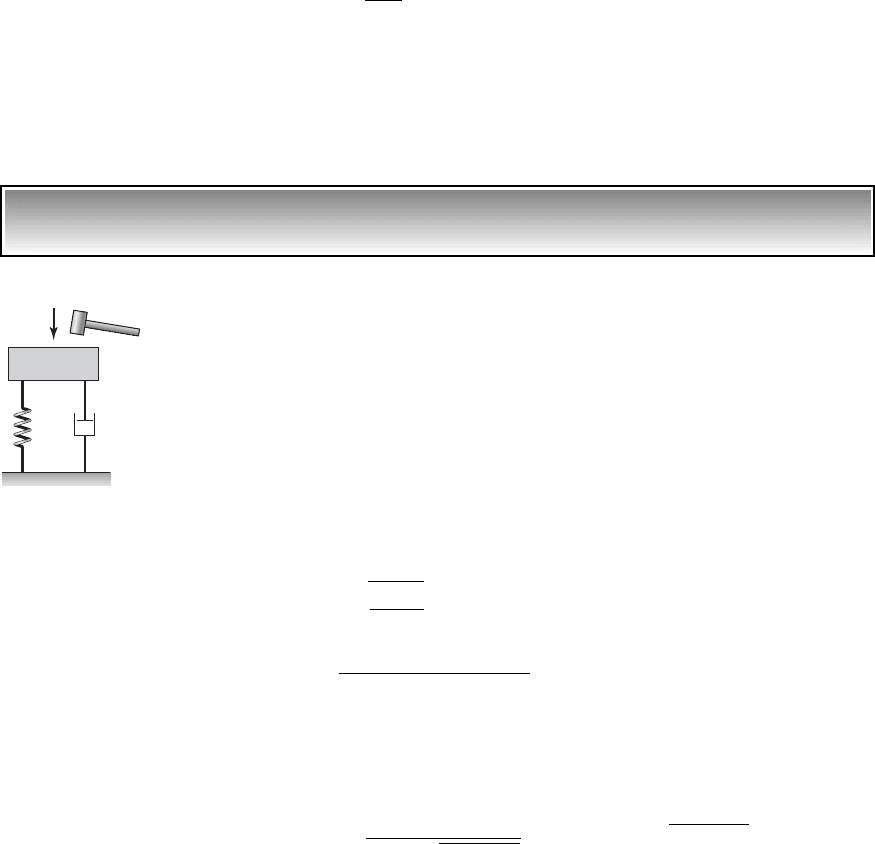
EXAMPLE 6.1
Response of a linear vibratory system to multiple impacts
4
An impact hammer is used to manually apply an impulse to a model of a sin-
gle degree-of-freedom system as illustrated in Figure 6.5. In experiments, a
single impact is preferred; however, it is difficult to realize only a single im-
pact and multiple impacts may occur. Assume that for a system with a mass
of 2 kg, stiffness of 8 N/m, and damping coefficient of 2 Ns/m, a double
impact of the form
5
occurs. We shall determine the system response and compare it to that ob-
tained when the second impact at t 1 s is absent.
For the given parameter values, the natural frequency v
n
and the damp-
ing factor z are determined, respectively, as
Since z 1, we have an underdamped system. Based on Eq. (6.4a), the
response of the system subjected to a single impact starts at t 0 and is
given by
0.26e
0.5t
sin11.94t 2 m
x
1
1t 2
1
2 221 0.25
2
e
10.2522t
sin12 21 0.25
2
t2 m
z
2 N
#
s/m
2 12 kg 2 12 rad/s2
0.25
v
n
B
8 N/m
2 kg
2 rad/s
f 1t 2 d1t 2 0.5d1t 12
h1t 2
1
mv
d
e
zv
n
t
sin1v
d
t2
6.2 Response to Impulse Excitation 293
4
D. J. Inman, Engineering Vibration, Prentice Hall, Upper Saddle River, NJ (2001).
5
Of course, a pulse of a finite-time duration rather than the delta function better approximates
the impact from a hammer. The responses to such pulse functions are discussed later in this
chapter.
c
k
Impact hammer
Mass m
FIGURE 6.5
System inertia element struck by an
impact hammer.

The response of the system subjected to the double impact is given by
Response to Response to second impact
first impact
The unit step function u(t 1) is used to indicate that the second impact affects
the response only for t 1 s. Before one second, that is before the second
impact occurs, the responses to the single and double impacts are identical,
as seen in the graphs of the responses provided in Figure 6.6. However, after
one second, the responses are different, as expected.
EXAMPLE 6.2
Use of an additional impact to suppress transient response
We shall extend Example 6.1 in the following manner. Consider the system
shown in Figure 6.1 that is subjected to an impulse of magnitude
s at
t 0. We then apply another impulse of magnitude
s at t t
o
. We shall
determine the time t
o
that minimizes the root mean square (rms) displacement
response of the mass x
rms
over the interval t
o
t T
n
, where, T
n
2np/ v
d
F
o
N
F
o
N
x
1
1t 2u1t2 0.13e
0.51t12
sin11.941t 122u1t 1 2 m
x
1
1t 2u1t2 10.26 0.5 2e
0.51t12
sin11.941t 122u1t 1 2 m
x
2
1t 2 x
1
1t 2u1t2 0.5x
1
1t 12u1t 12
294 CHAPTER 6 Single Degree-of-Freedom Systems Subjected to Transient Excitations
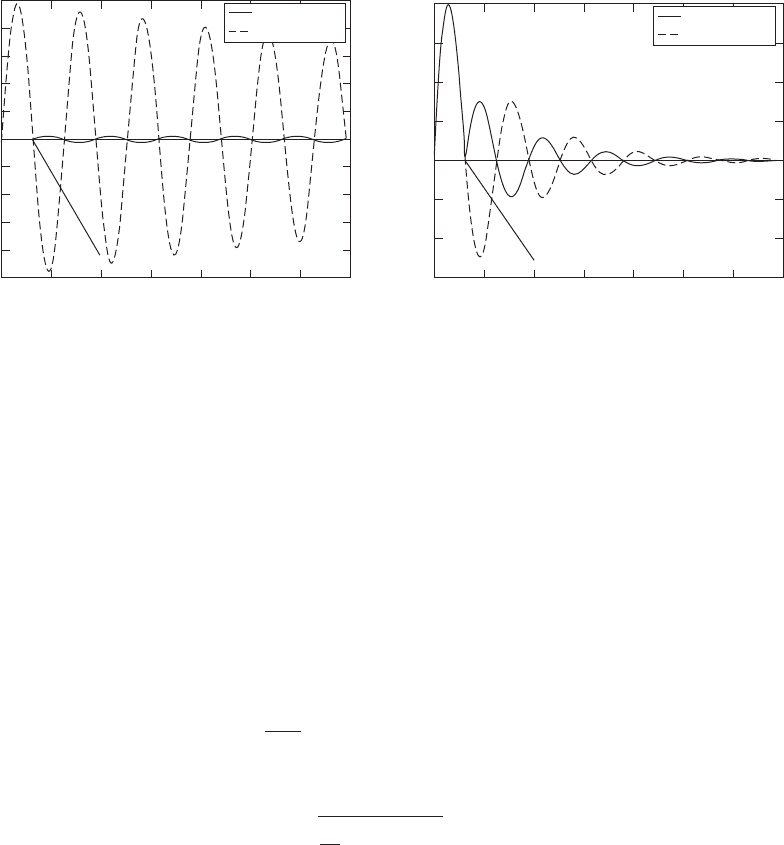
0 1 2 3 4 5 6
–0.1
–0.05
0
0.05
0.1
0.15
0.2
x(t) (m)
x
2
(t)
t (s)
x
1
(t)
FIGURE 6.6
Displacement responses to single impulse and two impulses one second apart.
⎫
⎬
⎭
⎫
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎭
6.2 Response to Impulse Excitation 295
and n is an integer. The quantity T
1
is the period of the damped oscillation.
The choice of n is somewhat arbitrary, but from Figure 6.2 we see that n
should increase as z decreases.
From the statement of the problem, we have that
(a)
Upon substituting Eq. (a) into Eq. (6.1a), we find that
(b)
The rms value over the specified time interval is given by
(c)
Equation (c) is solved numerically by using a standard optimization pro-
cedure
6
to determine the earliest time t
o
that gives the smallest value of x
rms
.
The results are shown in Figure 6.7 for z 0.01 and z = 0.15. It is seen from
the figure that for a very lightly damped system, the application of an impulse
at the nondimensional time v
n
t
o
3.142 virtually eliminates the magnitude
of the oscillations immediately after the application of the second impulse.
x
rms
B
1
T
n
t
o
T
n
t
o
x
2
1t 2dt
x1t 2
F
o
mv
d
3e
zv
n
t
sin 1v
d
t2u1t 2 e
zv
n
1tt
o
2
sin 1v
d
1t t
o
22u1t t
o
24
f 1t 2 F
o
3d1t2 d1t t
o
24
1
05
x(t)/(F
o
/m
n
)
10 15
n
t
o
=
3.142
20
(a)
(b)
n
t
25 30 35
0.8
0.6
0.4
0.2
0
–
0.2
–
0.4
–
0.6
–
0.8
–
1
0.8
05
x(t)/(F
o
/m
n
)
10 15
n
t
o
=
3.174
20
n
t
25 30 35
0.6
0.4
0.2
0
–
0.2
–
0.4
–
0.6
Two impulses
One impulse
Two impulses
One impulse
FIGURE 6.7
Response of the inertia element subjected to two impulses, where the second impulse has been applied so that the subsequent
response is minimized over the duration of interest: (a) z 0.05 and (b) z 0.15.
6
The MATLAB function fminsearch was used.

However, the application of the second impact has less effect as the damping
is increased. It is noted that the nondimensional half period of damped oscil-
lations is thus, for z 0.05, we have that
Therefore, for lightly damped systems, it is possible to
greatly reduce the magnitude of oscillations after the application of another
impulse if the second impulse is applied at a time approximately equal to the
half period of its damped oscillation.
EXAMPLE 6.3
Stress level under impulse loading
Consider the spring-mass-damper system shown in Example 6.1, and assume
that the top of the spring is welded to the mass. The welding is over an area
A
w
4 mm
2
, and the allowed maximum stress for the weld material is s
w,max
150 MN/m
2
. For an impulse of magnitude 100 N s, we shall determine
whether the stress level in the weld material will be below the maximum
allowed stress. It is assumed that z 0.25, m 200 kg, k 800 N/m, and
therefore, v
n
2 rad/s.
The impulse is given by Eq. (6.2) with f
o
100 N s, and the correspon-
ding displacement response of the system is determined from Eq. (6.4a).
Then, the force acting on the weld material is determined and from the
maximum value of this force, the maximum stress experienced by the weld
material during the motions is determined. This value is compared to the max-
imum allowed stress level, s
w,max
. The force acting on the weld material is
given by
(a)
The maximum force on the weld is given by Eq. (a) when x(t) x
max
, where
x
max
is given by Eq. (6.6). From Eq. (6.8), we find that
(b)
and, therefore,
(c)
Then, from Eq. (6.6), x
max
is
(d)
By using Eqs. (a) and (d), the maximum force on the weld is
(e)f
weld,max
kx
max
800 0.178 142.4 N
x
max
100
200 2
e
1.318/3.873
0.178 m
tan w tan 1.318 3.873
w tan
1
a
21 z
2
z
b tan
1
a
21 .25
2
.25
b 1.318 rad
f
weld
1t 2 kx1t2
#
#
v
n
T
1
/2 3.137.
v
n
T
1
/2 p/ 21 z
2
;
296 CHAPTER 6 Single Degree-of-Freedom Systems Subjected to Transient Excitations

6.2 Response to Impulse Excitation 297
Hence, the maximum stress s
w,max
experienced by the weld material is given by
(f )
This value is well below the maximum allowed stress level in the weld mate-
rial of 150 MN/m
2
. To exceed the given value of maximum allowed stress, the
impulse magnitude will have to be at least 4.2 times stronger than the present
impulse magnitude.
EXAMPLE 6.4
Design of a structure subjected to sustained winds
We shall determine an estimate of the outer diameter d
o
of a 10 m high steel
lamppost of constant cross-section that is subjected to sustained winds so that
the maximum transverse displacement of the lamps on top of the lamppost does
not exceed 5 cm. The mass of the lights on top of the lamppost is 75 kg. We as-
sume that the lamppost is a cylindrical tube whose inner diameter is 95% of d
o
,
that the system acts as a beam in bending, and that it can be modeled as a sin-
gle degree-of-freedom system. In addition, the damping ratio of the system is
assumed to be z 0.04. The magnitude of the turbulence-induced wind force
spectrum has been experimentally determined to be
(a)|F1jf 2| 400 fe
0.667f
N
s
w,max
f
weld,max
A
w
142.4 N
4 10
6
m
2
35.6 MN/m
2
0 2 4 6 8 10
0
50
100
150
200
250
f (Hz)
|F( jf)| (N)
FIGURE 6.8
Assumed wind-induced force spectrum acting on the lamppost.
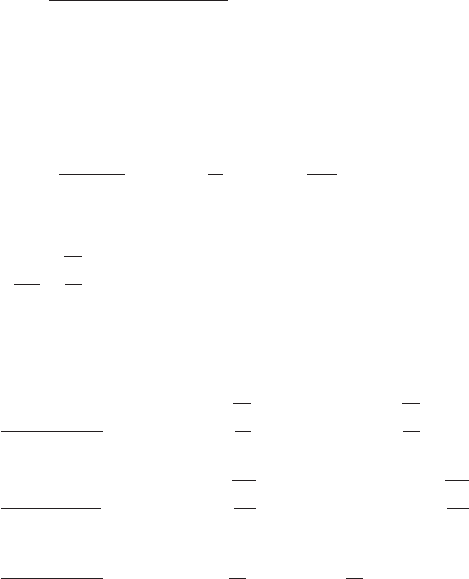
where f is frequency in Hz. The spectrum given by Eq. (a) is shown in
Figure 6.8.
Response in Frequency Domain
The solution is obtained by first determining from the displacement response
in the frequency domain the value of the equivalent stiffness k for which the
maximum amplitude is less than 0.05 cm over the entire frequency
range of . After the magnitude of the equivalent stiffness is known, the
value of d
o
is determined from the relationship for the stiffness of a cantilever
beam. Noting from Eq. (6.18) that the frequency-response function is
(b)
the displacement response in the frequency domain is then determined from
Eqs. (a) and (b), and Eq. (6.19). This response is converted from the radian
frequency notation v to frequency f in Hz resulting in
(c)
where the natural frequency f
n
in Hz is
(d)
Upon substituting Eqs. (d) and (a) into Eq. (c) and noting that m 75 kg and
z 0.04, we obtain
(e)
We now plot Eq. (e) for three values of k: 20,000, 30,000, and
40,000 N/m. The results are shown in Figure 6.9. It is seen that as the stiff-
ness increases, the natural frequency increases and the maximum magnitude
of |X( jf )| decreases. This decrease is brought about by the fact that the spec-
tral amplitude of |F( jf )| diminishes as f increases, when f is greater than about
1.6 Hz. Since this magnitude of the forcing is decreasing in this frequency re-
gion, the magnification by the system’s frequency response function |H( jf )|
in the damping-dominated region is magnifying a smaller quantity; hence, the
peak magnitude of |X( jf )| becomes smaller.
400 fe
0.667 f
k
ca1 2960.9
f
2
k
b
2
18.95
f
2
k
d
1/2
400 fe
0.667 f
k
ca1 a2pf
B
75
k
b
2
b
2
a4p10.042f
B
75
k
b
2
d
1/2
0X1jf 20
400 fe
0.667 f
k
ca1 a2pf
B
m
k
b
2
b
2
a4pzf
B
m
k
b
2
d
1/2
f
n
1
2p B
k
m
0X1jf 20
0F1jf 20
k
ca1 a
f
f
n
b
2
b
2
a
2zf
f
n
b
2
d
1/2
G1jv2
1
m31zv
n
jv2
2
v
d
2
4
|F1jf 2|
|X1jf 2|
298 CHAPTER 6 Single Degree-of-Freedom Systems Subjected to Transient Excitations
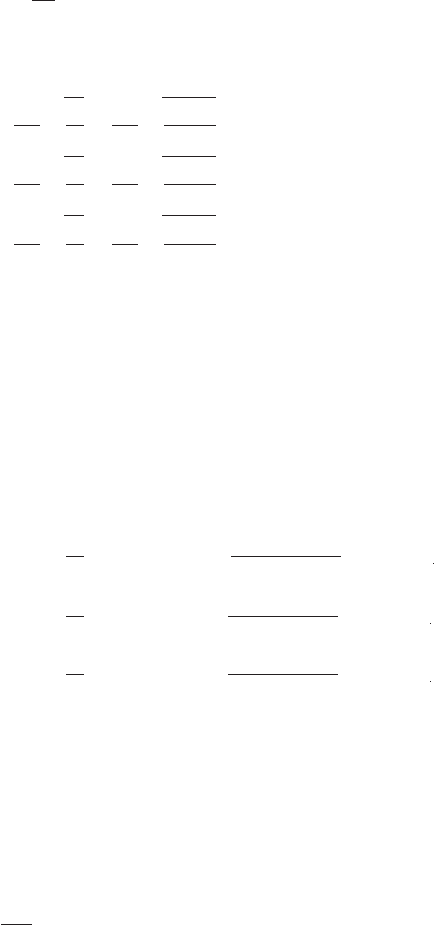
Another way to determine approximately the peak responses is to recall
the response of a system in the damping-dominated region given by
Eq. (5.29); that is,
(f)
Thus, for z 0.04, H(1) 12.5. The values of |F( jf )| at the three the natural
frequencies corresponding to the three stiffness values k
j
are, respectively,
(g)
Then, from Eqs. (a) and (g), we have that
(h)
These values could also have been obtained directly from Figure 6.8, but with
less precision. Consequently, the peak magnitudes of the displacements at
these three frequencies are, respectively,
(i)
It is seen that these values correspond to their respective counterparts in
Figure 6.9.
Lamppost Parameters
The value of k that produces a maximum magnitude of |X( jf )| equal to 5 cm
is determined numerically
7
to be 34,909 N/m. To determine the diameter of
the cylindrical support, we note from entry 4 in Table 2.3 that
(j)k
3EI
L
3
0X1jf
n3
20
1
k
3
0F1jf
n3
20H11 2
126.4 12.5
40000
3.95 cm
0X1jf
n2
20
1
k
2
0F1jf
n2
20H11 2
152.5 12.5
30000
6.35 cm
0X1jf
n1
20
1
k
1
0F1jf
n1
20H11 2
183.6 12.5
20000
11.5 cm
0F1jf
n3
20 400f
n3
e
0.667 fn3
400 3.68e
0.667 3.68
126.4 N
0F1jf
n2
20 400f
n2
e
0.667 fn2
400 3.18e
0.667 3.18
152.5 N
0F1jf
n1
20 400f
n1
e
0.667 fn1
400 2.6e
0.667 2.6
183.6 N
f
n3
1
2p B
k
3
m
1
2p B
40000
75
3.68 Hz
f
n2
1
2p B
k
2
m
1
2p B
30000
75
3.18 Hz
f
n1
1
2p B
k
1
m
1
2p B
20000
75
2.6 Hz
H11 2
1
2z
6.2 Response to Impulse Excitation 299
7
The MATLAB function fzero and the MATLAB function fminbnd from the Optimization
Toolbox were used.
