Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.


The reduction in transmissibility, denoted R, is a measure of the amount
of force or displacement that doesn’t get through; thus,
R 1 TR (5.105)
EXAMPLE 5.12
Design of a vibration isolation mount
It has been found that when a 100 kg machine rotating at 1200 rpm is mounted
directly to the floor it generates 180 N of force on the floor. It is decided that
the machine should be isolated from the floor so that the magnitude of the mo-
tion of the machine is less then or equal to 2 mm and that the TR is 10% or
less. We shall determine the isolation system’s spring stiffness k and damping
constant c.
If the magnitude of x(t) is X
m
and the magnitude of the force transmitted
to the floor is F
m
, then from Eqs. (5.17) and (5.102) and the given parameters,
we find that
(a)
and from Eq. (5.104) that
(b)
where v/v
n
and v 1200 (2p)/60 125.66 rad/s. From Eqs. (a) and
(b), we obtain
(c)
and that
(d)
From Figure 5.34, we see that if we assume that z 0.1, then must be
greater than approximately 4, which means that v
n
v/125.66/4
31.415 rad/s. Thus, from the definitions of and v
n
,
and
(e)
We see from Eq. (a) that X
m
1800 0.0666/98690 0.0012 m, which is
less than 0.002 m.
The isolation system’s damping constant is
c 2zmv
n
2 0.1 100 31.4 628 Ns/m
0.0666
H12 311
2
2
2
12z2
2
4
1/2
311 4
2
2
2
12 0.1 42
2
4
1/2
k mv
2
n
100 31.415
2
98690 N/m
k
F
o
X
m
H12
1800 N
10.002 m 2
H12 90 10
4
H12 N/m
F
o
F
m
TR
180
0.1
1800 N
TR H
mb
1 2 0.1
F
m
F
o
H
mb
1 2 180 N
X
m
F
o
k
H12 2 mm
240 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations
5.7 Vibration Isolation 241
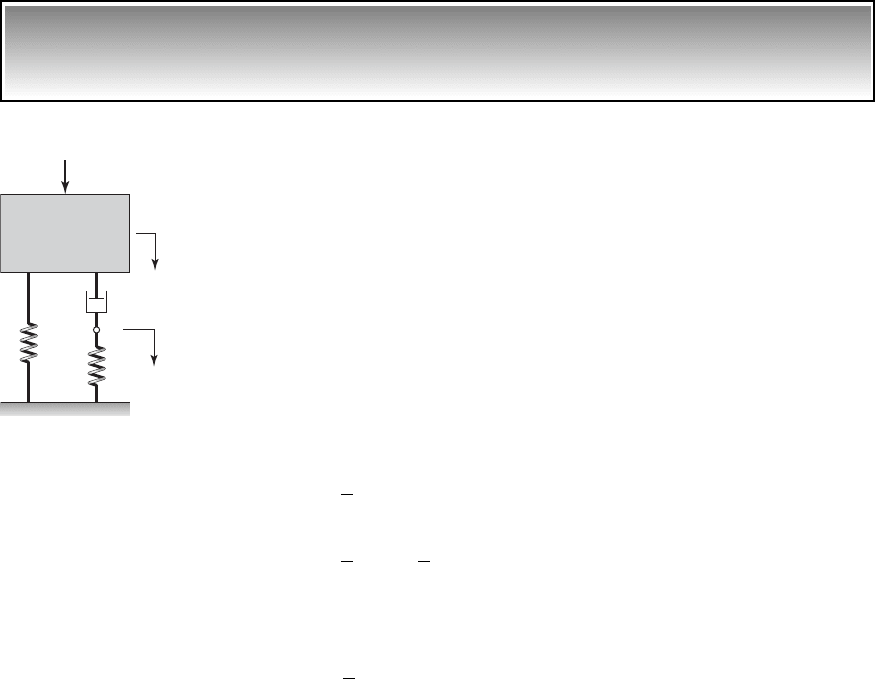
EXAMPLE 5.13 Modified system to limit the maximum value of TR due to
machine start-up
The isolation that is indicated by Eq. (5.105) is valid only when the excitation
frequency is much greater than the natural frequency of the system, and as-
sumes that the system always operates at this frequency. There are many sys-
tems, however, that operate at a frequency much greater than the natural fre-
quency, but are cycled so that they turn on and off on a regular and frequent
basis. As these systems get up to operating speed (frequency) they must pass
through the system’s resonance region, where larger forces/displacements are
temporarily transmitted to the ground/base.
17
A modification to the system that
can reduce the maximum value of TR in the neighborhood of the resonance is
shown in Figure 5.35. The modification includes an additional spring k
2
be-
tween the damper and the base, which, we recall from Example 4.7, results in
a Maxwell element. We shall now re-derive the governing equation of this
system using Lagrange’s equations.
The kinetic energy and potential energy for this system are, respectively,
(a)
and the dissipation function is
(b)
By using Eq. (3.41), the Lagrange equations, with N 2, q
1
x
1
, q
2
x
2
,
Q
1
f(t), and Q
2
0, we obtain
(c)
Although the inertia element shown in Figure 5.35 is described in terms
of a single coordinate—that is, x
1
—here, the additional variable x
2
is also
needed to determine the damper force and the spring force associated with
k
2
. As discussed later on, the transmitted force depends on the variable x
2
.
18
c1x
#
1
x
#
2
2 k
2
x
2
0
mx
$
1
c1x
#
1
x
#
2
2 k
1
x
1
f 1t 2
D
1
2
c1x
#
1
x
#
2
2
2
V
1
2
k
1
x
1
2
1
2
k
2
x
2
2
T
1
2
mx
#
2
1
f(t)
x
1
(t)
x
2
(t)
k
2
k
1
c
m
FIGURE 5.35
Single degree-of-freedom system
with an additional spring added in
series with the damper.
17
It is mentioned that if a vibratory system such as a rotating machine is ramped up to operate at
a high frequency, then to attenuate the response while passing through resonance, one will need
some amount of damping.
18
As discussed in Example 4.7, the system shown in Figure 5.35 is said to be a system with one
and a half degrees of freedom: One of the governing equations is a second-order differential
equation, while the other one is a first-order differential equation.

Introducing the damping factor z c/(2mv
n
) and the natural frequency
Eq. (c) is written as
(d)
where g k
2
/k
1
.
We assume that the initial conditions are zero and take the Laplace trans-
forms of Eqs. (d). This results in
(e)
where X
1
(s) is the Laplace transform of x
1
(t), X
2
(s) is the Laplace transform
of x
2
(t), and F(s) is the Laplace transform of f(t). Solving for X
1
(s) and X
2
(s)
from Eqs. (e), we obtain
(f)
where
(g)
We are interested in the dynamic force transmitted to the ground, which
for the configuration shown in Figure 5.35, is
F
T
k
1
x
1
k
2
x
2
(h)
Taking the Laplace transform of Eq. (h) and using Eqs. (f) we obtain
(i)
From Section 5.3.4, we see that the transmissibility ratio is obtained by
setting s jv in Eq. (i) and then taking its magnitude, which results in
(j)
When g →∞, that is, k
2
becomes rigid, Eq. (j) becomes H
mb
() given by
Eqs. (5.82).
TR `
F
T
1jv2
F1jv 2
`
2g
2
32z11 g 24
2
2g
2
11
2
2
2
12z2
2
31 g
2
4
2
F
T
1s 2
F1s 2
v
n
2
D
3
1s 2
3C1s2 gB1s 24
C1s 2 gv
n
2
2zv
n
s
B1s 2 2zv
n
s
D
3
1s 2 gv
2
n
1s
2
v
n
2
2 2zv
n
s1s
2
v
n
2
31 g42
X
2
1s 2
F1s 2
m
B1s 2
D
3
1s 2
X
1
1s 2
F1s 2
m
C1s 2
D
3
1s 2
2 zv
n
sX
1
1s 2 1gv
n
2
2zv
n
s2X
2
1s 2 0
1s
2
2zv
n
s v
n
2
2X
1
1s 2 2zv
n
sX
2
1s 2
F1s 2
m
2 zv
n
1x
#
1
x
#
2
2 gv
2
n
x
2
0
x
$
1
2zv
n
1x
#
1
x
#
2
2 v
n
2
x
1
f1t 2
m
v
n
1k
1
/
m
,
242 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations
5.7 Vibration Isolation 243
0.5 1 1.5 2 2.5 3 3.5 4
1.5
2
2.5
3
3.5
4
4.5
5
z 0.15
z 0.2
z 0.25
z 0.3
z 0.4
z 0.5
g
TR
max
(a)
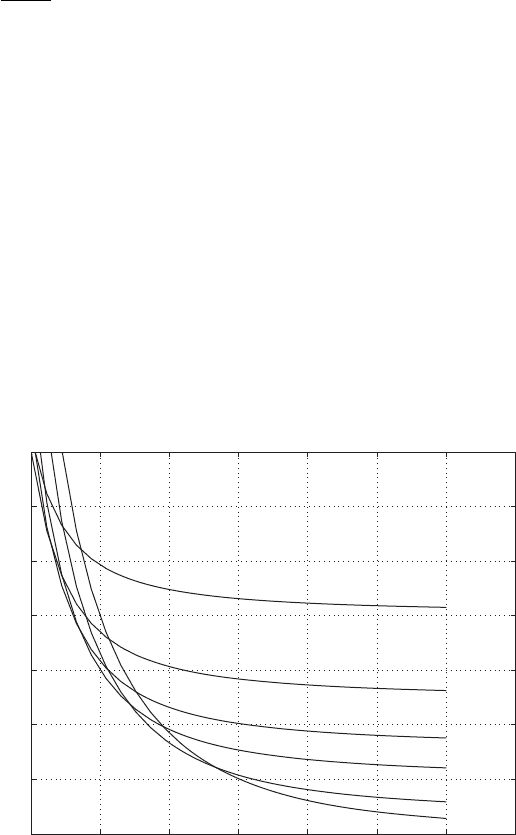
FIGURE 5.36
(a) TR
max
as a function of z and g.
For a fixed value of z and g, the frequency ratio at which TR is an ex-
tremum,
max
, corresponds to
(k)
After evaluating
19
Eq. (k), we obtain
where y
2
and
The real root of this equation is denoted as .
The real values of TR
max
which are determined at
max
are plotted in Fig-
ure 5.36 for several values of g and z. We see, for example, that TR
max
will al-
ways be less than 2.5 when g 2 and z 0.25. In this case, if the operating
y
max
2
max
C
4
2g
4
C
3
2g
4
16g
2
11 g2z
2
C
2
12g
2
z
2
4z
2
11 g2
2
g
2
3211 g2
3
z
4
C
1
32z
4
11 g2
2
C
1
y
3
C
2
y
2
C
3
y C
4
0
01TR 2
0
0
19
We have used diff from the MATLAB Symbolic toolbox and roots to obtain the numeri-
cal values.
frequency ratio is 5, then we find from Eq. (j) that TR 0.1; that is, less
than 10% of the force will be transmitted to the base. In addition, on the way
to reaching this operating speed, the TR will not exceed 2.5.
5.8 ENERGY DISSIPATION AND EQUIVALENT DAMPING
As discussed in the earlier chapters, viscous damping is one form of damping
model. Other types of damping models include Coulomb or dry friction
damping, fluid or velocity-squared damping, and structural or material damp-
ing. The viscous damping model as presented in Chapter 2 can be a linear or
nonlinear model, while the Coulomb or dry friction model and the fluid model
are nonlinear. In addition, the structural damping model is a linear one. We
shall now relate the three damping models to the viscous damping model
through a quantity called the equivalent viscous damping c
eq
, which is the
value of the damping coefficient c that is required in order to dissipate the
same amount of energy per period of forced harmonic oscillation. Since
the energy consideration is on a per cycle basis, the following results are only
applicable to a system subjected to harmonic excitation.
In a vibratory system, the spring force and inertia force are conservative
and hence, the work done by each of the forces over one cycle of forced os-
cillation is zero.
20
Therefore, in determining the energy dissipation in a vi-
bratory system, we only pay attention to the damper or dissipation force.
244 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations
20
See Exercise 2.28 for the work done by the spring force.
0.5 1 1.5 2 2.5 3 3.5
0.95
1
1.05
1.1
1.15
1.2
1.25
1.3
1.35
z 0.15
z 0.2
z 0.25
z 0.3
z 0.4
g
Ω
max
z 0.5
(b)
FIGURE 5.36 (continued )
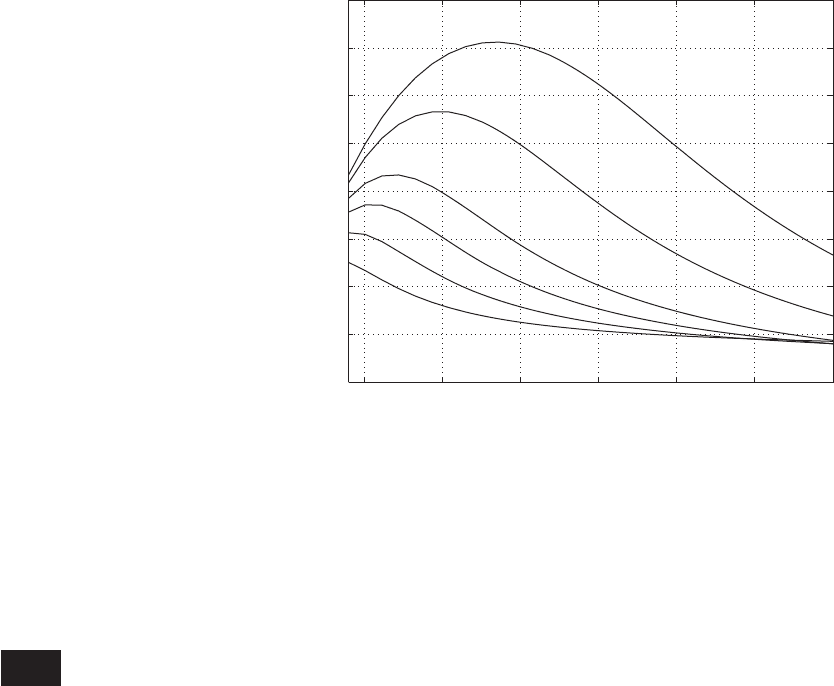
(b)
max
as a function of z and g.

If the dissipation force is F
D
, then the energy dissipation as discussed in
Section 2.4 is given by the work done; that is,
(5.106)
For harmonic excitations of linear systems after the transients settle down, it
can be assumed that the displacement and velocity responses have the forms
(5.107)
where the displacement and the velocity responses have the period 2p/v,
where v is the forcing frequency. It can be shown that the work done by the
external force acting on the system is equal to E
d
over one cycle of forcing.
See Exercise 5.18.
Viscous Damping
From Eq. (2.46), we have that for a linear viscous damping model
(5.108)
Upon substituting Eq. (5.108) into (5.106), the energy dissipated is
(5.109)
On substituting the velocity response from Eqs. (5.107) into Eq. (5.109), we
obtain
(5.110)
From Eq. (5.110), it is clear that the energy dissipated is linearly proportional
to the damping coefficient c and the excitation frequency v, and proportional
to the square of the displacement amplitude X
o
.
If f(t) F
o
sin(t), then using Eq. (5.9) another form of Eq. (5.110) is
(5.111)
where
(5.112)X
o
F
o
k
H12
F
2
o
k
pH12sin 1u122 F
o
X
o
psin 1u1 22
E
viscous
2p/
0
f 1t2x
#
1t 2dt
F
2
o
H12
k
2p/
0
sin 1t2cos 1t u122dt
E
viscous
cv
2
X
2
o
2p/v
0
cos
2
1vt f2dt cpvX
2
o
E
viscous
c
2p/v
0
x
#
2
1t 2dt
F
D
cx
#
1t 2
x
#
1t 2 vX
o
cos 1vt f 2
x1t 2 X
o
sin 1vt f 2
E
d
F
D
dx
F
D
dx
dt
dt
F
D
x
#
dt
5.8 Energy Dissipation and Equivalent Damping 245
is the magnitude of the displacement of the mass at . We see from
Eq. (5.111) that E
viscous
will be a maximum when u() p/2. It was shown
in Eqs. (5.29) and (5.31) that at 1, u(1) p/2 and the force and veloc-
ity are in phase. Therefore, from Eq. (5.111), we see that the external work
that is available to overcome the viscous dissipation per cycle is a maximum
at 1. Hence, we should expect the system response to be a maximum at
1; that is, at the system’s natural frequency.
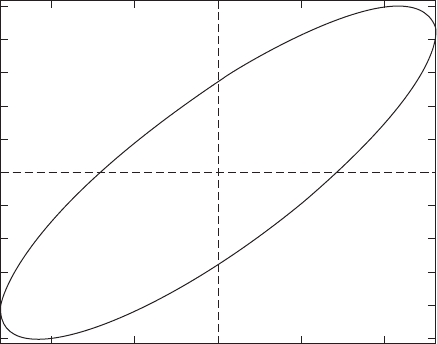
Another way to visualize the energy dissipation per cycle is to plot the
instantaneous force as a function of instantaneous displacement, which is
shown in Figure 5.37 for the specific values of z 0.35 and 0.6. The
force-displacement curve is called a hysteresis loop
21
, and the area enclosed
by this loop is equal to the energy lost per forcing cycle E
viscous
.
Coulomb (Dry Friction) Damping
From Eq. (2.52), we have that the damping force magnitude is
(5.113)
and from Eq. (2.53) the energy dissipated is
(5.114)
where sgn is the signum function introduced in Section 2.4. On substituting
the velocity response from Eqs. (5.107) into Eq. (5.114) and integrating, we
arrive at
E
coulomb
mmg
2p/v
0
sgn1x
#
2x
#
1t 2dt
F
D
mmg sgn1x
#
2
246 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations
1
0.8
0.6
0.4
0.2
0
f(t)/F
o
x(t)/(F
o
/k)
0.2
0.4
0.6
0.8
1
1 0.5
0 0.5 1
FIGURE 5.37
Hysteresis loop for z 0.35 and 0.6 in Eq. (5.17).
21
S. S. Rao, Mechanical Vibrations, 4th ed., Prentice Hall, Upper Saddle River, NJ, 2004, p. 165.

(5.115)
where the variable of integration j vt.
To determine the equivalent viscous damping, we set E
viscous
equal to
E
Coulomb
. Thus, from Eqs. (5.115) and (5.110), we obtain
c
eq
pvX
2
o
4mmgX
o
which leads to
(5.116)
where c
eq
is the equivalent viscous damping. Note that this equivalence of
damping model is based on energy considerations only, and it should not be
inferred that in this and other cases that the linear system with the equivalent
viscous damping has the same stability properties as the original system.
Furthermore, it is noted from Eq. (5.116) that unlike in the case of a system
with viscous damping, in the case of a system with dry friction the equivalent
damping coefficient is inversely proportional to the excitation frequency and
the displacement response amplitude X
o
.
Fluid (Velocity-Squared) Damping
From Eq. (2.54), we stated that the magnitude of the damping force is
(5.117)
where c
d
is given by Eq. (2.55). After substituting Eq. (5.117) into Eq. (5.106),
the energy dissipated is determined from
(5.118)
On substituting the velocity response from Eqs. (5.107) into Eq. (5.118), we
arrive at
(5.119)
where the integration has been carried out in a manner similar to that used to
obtain Eq. (5.115).
E
fluid
c
d
v
2
X
3
o
2p
0
sgn1cosj2cos
3
jdj
8
3
c
d
v
2
X
3
o
E
fluid
c
d
2p/v
0
sgn1x
#
2x
#
3
dt
F
D
c
d
x
#
2
sgn1x
#
2 c
d
0x
#
0x
#
c
eq
4mmg
pvX
o
4mmgX
o
mmgX
o
c
p/2
0
cosjdj
3p/2
p/2
cosjdj
2p
3p/2
cosjdj d
E
coulomb
mmgX
o
2p
0
sgn1cos j 2cos jdj
5.8 Energy Dissipation and Equivalent Damping 247

To determine the equivalent viscous damping, we set E
viscous
from
Eq. (5.110) equal to E
fluid
given by Eq. (5.119). Thus, we arrive at
which leads to
(5.120)
Thus, the equivalent viscous damping is linearly proportional to the excitation
frequency and the response amplitude.
Structural (Material) Damping
In Eq. (2.57), we stated that the magnitude of the damping force is given by
(5.121)
where b is an empirically determined constant. After substituting Eq. (5.121)
into Eq. (5.106), the energy dissipated is
(5.122)
On substituting the velocity response from Eqs. (5.107) into Eq. (5.122), the
resulting expression is
(5.123)
To determine the equivalent viscous damping for this case, we set
E
viscous
from Eq. (5.110) equal to E
structural
in Eq. (5.123). This leads to
from which we obtain
(5.124)c
eq
2kb
v
c
eq
pvX
o
2
2kpbX
2
o
2kpbX
2
o
3p/2
p
sin j cos jdj
2p
3p/2
sin j cos jdj d
kpbX
2
o
c
p/2
0
sin j cos jdj
p
p/2
sin j cos jdj
E
structural
kpbX
2
o
2p
0
sgn1cos j20sin j 0cos jdj
E
structural
kpb
2p/v
p
sgn1x
#
20x 0x
#
dt
F
D
kpb sgn1x
#
20x 0
c
eq
8c
d
vX
o
3p
c
eq
pvX
2
o
8
3
c
d
v
2
X
3
o
248 CHAPTER 5 Single Degree-of-Freedom Systems Subjected to Periodic Excitations

As in the case of dry friction, the equivalent viscous damping for structural
damping is inversely proportional to the excitation frequency.
We now place the expressions for the equivalent viscous damping c
eq
in
their respective governing equations. The restriction for each of these equa-
tions is that the forcing function must be a harmonic excitation.
Viscous damping
(5.125)
Coulomb (dry friction) damping
(5.126)
Fluid (velocity-squared) damping
(5.127)
Structural (material) damping
(5.128)
In what has been presented above, systems with different forms of damp-
ing have been represented by equivalent systems with equivalent viscous
damping. It is repeated that these equivalent systems may not always capture
the true stability properties of the original systems, in particular, in cases like
Eqs. (5.126) and (5.127). We see that these equations are nonlinear equations,
because the equivalent damping term is a function of X
o
, the magnitude of the
displacement response.
Forced Response of System with Structural Damping
The solution to Eq. (5.128) is obtained from Eq. (5.17) by replacing c with
2kb/v or, equivalently, z b/. Thus, in this case,
(5.129)
where the associated amplitude response H
st
() and the phase response u
st
()
are given by
(5.130)
Graphs of Eqs. (5.130) are given in Figure 5.38. It is observed that the value
of at which H
st
() is a maximum always occurs at 1.
u
st
1 2 tan
1
2b
1
2
H
st
1 2
1
21
2
2
2
4b
2
x
st
1t 2
F
o
k
H
st
1 2sin 1t u
st
1 22
mx
#
2kb
v
x
#
kx F
o
sin 1vt 2
mx
#
8c
d
vX
o
3p
x
#
kx F
o
sin 1vt 2
mx
#
4mmg
pvX
o
x
#
kx F
o
sin 1vt 2
mx
$
cx
#
kx F
o
sin 1vt 2
5.8 Energy Dissipation and Equivalent Damping 249
