Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

6.6 Finding the shear centre for a closed section 325

where q

is associated with the force V

through the shear centre and q

with the

equivalent torque. It then follows that

= 0 , (6.48)

from (6.45) and

, (6.49)

from (6.29). We can therefore write

qdS

(6.50)

and substitution in (6.46) yields

2AG

qdS

. (6.51)

Thus, if the line of action of V

is prescribed, we ﬁrst use the procedure of §6.4.1 to

determine q throughout the section and then substitute into (6.51) to determine the

twist

Example 6. 7

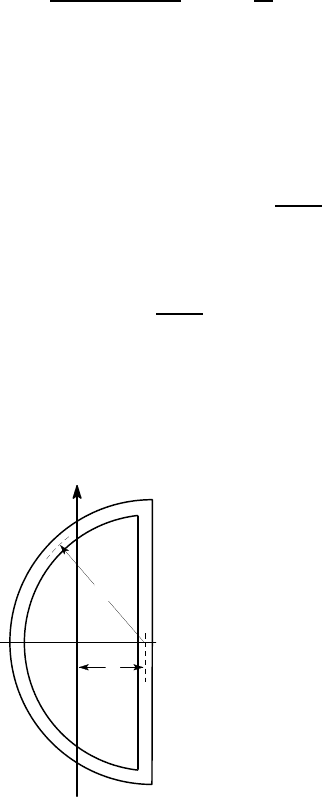
The closed semi-circular section of Figure 6.35 is made of aluminium (G = 30 GPa)

and has dimensions a=30 mm, t =2 mm. Find the location of the shear centre. Hence

or otherwise, ﬁnd the twist per unit length when the beam is loaded by a shear force

=2 kN passing through the point O as shown in Figure 6.35

In determining the location of the shear centre, the ﬁrst two steps are identical

with those of Example 6.5 above and lead to the results

4.474a



1 −



= −

cos

2.237a

+C ,

where the coordinates y,

are deﬁned in Figures 6.35 (a,b) and C is an unknown

constant.

It follows that

qdS

−a



4.474a



1 −





−



−

cos

2.237a



4.474t

−

3 ×4.474t

2aC

−

2.237t

(

+ 2)aC

−

6.711t

Notice that the integrals must be written so that the lower limit is smaller than the

upper limit. It is not necessarily correct to write them such that they pass around the

326 6 Shear and Torsion of Thin-walled Beams

section always in the same sense (clockwise or anticlockwise), since all we are doing

here is performing a summation.

To satisfy equation (6.45), we require

C =

(

+ 2)(6.711a)

= 0.116

To ﬁnd the shear centre, we equate the moment of the distribution about O to that

of V

, as in §6.4.1. Only the stresses in the curved segment have a non-zero moment

arm (= a). The distance c is deﬁned to place the shear centre on the left of O as in

Figure 6.42, so the moment V

×c is deﬁned as clockwise positive. This convention

has to be observed also in taking moments for the distribution and we obtain

×c = −

−

= −

C +

2.237

Substituting for C and dividing through by V

, we ﬁnd

c = −

a(0.116) +

2.237

= 0.530a ,

which determines the location of the shear centre, shown in Figure 6.42. Notice that

for a convex closed section, the shear centre is always inside the section. Also, since

the torsional stiffness of closed sections is generally large (see §6.5.1), the exact

location of the shear centre is of comparatively little importance, since not much

twist will be produced by applying a shear force through a different point.

c = 0.53a

Figure 6.42: Location of the shear centre for the closed semi-circular section

We can use this result to determine the twist by noting that the shear force acting

through O is equivalent to an equal force through the shear centre (which produces

no twist) and an equivalent anticlockwise torque

T = V

c = 0.53V

a .

6.6 Finding the shear centre for a closed section 327

The area enclosed by the section is

A =

and

(

+ 2)a

0.53V

+ 2)a

0.53(

+ 2)V

Substituting the given values, we obtain

0.53(

+ 2) ×2000

×30

×10

−6

×30 ×10

×2 ×10

−3

= 0.010 rad/m .

An alternative method for determining the twist per unit length is to substitute

the shear ﬂow corresponding to the line of action through O directly into equation

(6.51). We showed in Example 6.5 that q is then given by the above expressions with

C =0.285a, so

qdS

(

+ 2)aC

−

6.711t

0.285(

+ 2)V

−

6.711t

= 0.869

We then have

0.869V

2AGt

0.869 ×2000

×30

×10

−6

×30 ×10

×2 ×10

−3

= 0.010 rad/m

as before.

6.6.2 Multicell sect ions

Figure 6.43 shows a closed thin-walled section with an internal partition which di-

vides the enclosed area into two cells.

(a) (b)

Figure 6.43: (a) Multicell section, (b) equivalent shear ﬂow

328 6 Shear and Torsion of Thin-walled Beams

If this section is loaded in torsion, the arguments of §6.5 show that the shear ﬂow

must be constant in each segment of the wall, but there is now the possibility that part

of the shear ﬂow passes down the partition as shown. Another way to think of this

is to deﬁne a ﬂow q

anticlockwise around each cell as shown in Figure 6.43 (b), in

which case superposition shows that the ﬂow in the partition will be q

−q

upwards,

as in Figure 6.43 (a).

The equilibrium argument of §6.5 leads to the result

T =

∑

i=1

, (6.52)

where A

is the area enclosed by the ith cell and N is the total number of cells, but for

N > 1 this is insufﬁcient to determine the shear ﬂows q

in the individual cells for a

given torque T . To complete the solution, we need to impose the compatibility con-

dition that the individual cells twist through the same angle. Using equation (6.51),

this yields

qdS

= .... , (6.53)

which provides just sufﬁcient additional equations to determine the q

An essentially similar procedure can be used for a multicell section loaded by a

shear force. The arguments of §6.4 enable us to determine how q varies in any wall

segment, except that an additional arbitrary constant is introduced by each partition.

The compatibility conditions (6.53) provide the additional equations needed to deter-

mine these constants. For more details of this procedure, see Cook and Young, §§8.8,

9.9.

6.7 Torsion of thin-walled open sections

We have seen in §§6.4–6.6 that closed sections transmit shear forces and torques

by essentially the same mechanism, generating a shear stress that is approximately

uniform through the wall thickness. For open sections, this form of distribution can

arise only for shear forces whose line of action passes through the shear centre and

it can never arise from torsion alone.

We recall from §6.1 that the shear stress must always be tangential to the local

wall of the section, because any local normal component would imply a complemen-

tary shear stress on the traction-free wall of the beam. The only distribution satisfying

this condition in a thin-walled open section which is equivalent to a torque is that il-

lustrated in Figure 6.44 (a), where the shear stress passes along one side of the wall

and back along the other.

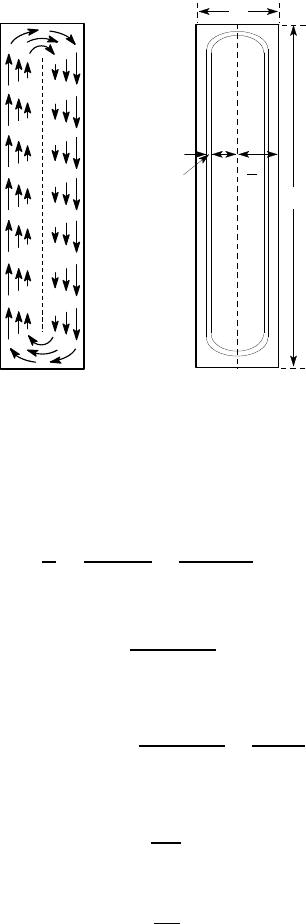
An approximate treatment of this problem can be obtained by considering the

section to be made up of a set of nested thin-walled tubes of wall thickness

y, one

of which is illustrated in Figure 6.44 (b). If the thickness t is constant and we neglect

the small curved regions near the ends, each of these tubes will have parallel walls

and the area enclosed and the perimeter will be approximately

6.7 Torsion of thin-walled open sections 329

A = 2yb ; S = 2b , (6.54)

respectively, where y is measured normal to the mean line, as shown in Figure

6.44 (b).

δy

(a) (b)

Figure 6.44: (a) Shear stress distribution due to torsion in an open section, (b)

elemental thin-walled tube contained within the section

If a given tube carries an elemental torque

T , the twist per unit length will be

T S

8by

, (6.55)

from (6.34) and hence

T =

8by

. (6.56)

All the tubes must have the same twist and hence the total torque transmitted is

T =

t/2

8by

. (6.57)

Notice that this relation can be written

T L

, (6.58)

where

K =

. (6.59)

Eliminating

/L between equations (6.56, 6.57), we obtain

330 6 Shear and Torsion of Thin-walled Beams

T =

24Ty

(6.60)

and hence the shear stress is given by (6.29) as

24Ty

4yb

6Ty

. (6.61)

Thus, the shear stress varies linearly through the thickness, reaching a maximum at

y=t/2 of

max

. (6.62)

This solution is inexact in regions near the ends of the section, but as long as b ≫t,

the error involved will be small.

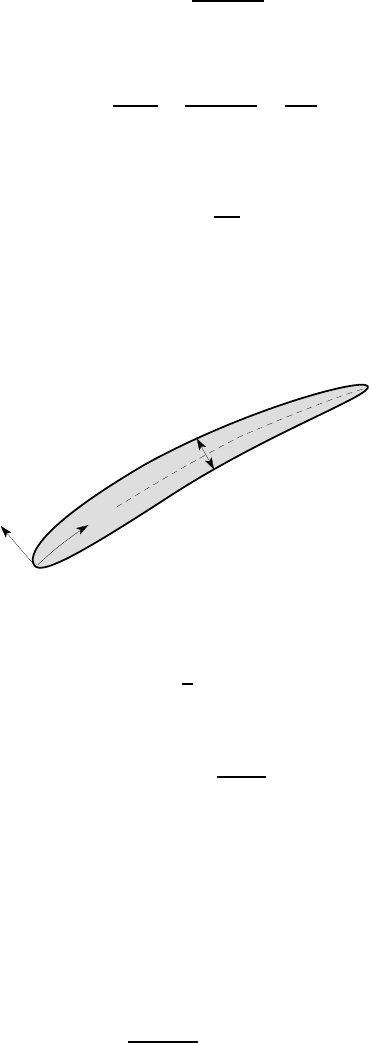
We have developed the argument for the case where the thickness t is constant,

but it is easily extended to sections where t is a function of distance

along the

section, as shown in Figure 6.45.

ξ = b

t (ξ)

Figure 6.45: Thin-walled open section with variable thickness

We ﬁnd that

K =

(6.63)

and the maximum shear stress is

max

(

) =

Tt(

)

. (6.64)

Thus, the absolute maximum shear stress occurs at the thickest part of the section.

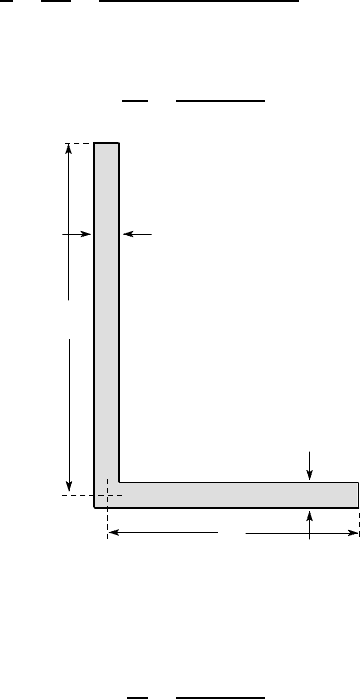
Example 6. 8

The steel angle beam of Figure 6.46 is loaded by a torque of 10 Nm. Find the maxi-

mum shear stress and the twist per unit length (G

steel

=80 GPa).

The perimeter of the section is 120 mm, so

K =

120 ×5

= 5000 mm

6.7 Torsion of thin-walled open sections 331

from equation (6.59). The twist per unit length is therefore

80 ×10

×5000 ×10

−12

= 0.025 rad/m

and the maximum shear stress is

max

3 ×10, 000

120 ×5

= 10 MPa.

all dimensions in mm

Figure 6.46

Alternatively, we could ﬁnd the maximum shear stress from equation (6.64)

which gives

max

10,000 ×5

5000

= 10 MPa

as before.

Notice that this torque gives a modest shear stress (typical steels have yield

stresses over 100 MPa), but produces quite a substantial twist (≈14

per metre).

This illustrates the fact that open sections are surprisingly ﬂexible in torsion. Notice

also how easy these equations are to use.

6.7.1 Loading of an open section away from its shear cent re

These results can be combined with those of § §6.1–6.3 to determine the shear stresses

and the twist for an open section loaded by a shear force whose line of action does

not pass through the shear centre. The procedure is:-

332 6 Shear and Torsion of Thin-walled Beams

(i) Find the shear stress distribution due to an equal shear force acting through the

shear centre (§6.1).

(ii) Find the location of the shear centre (§6.2).

(iii) Find the equivalent torque due to the offset of the prescribed line of action of

the shear force from the shear centre.

(iv) Find the stresses and the twist due to this torque (§6.7).

(v) Superpose the results from (i) and (iv).

Example 6. 9

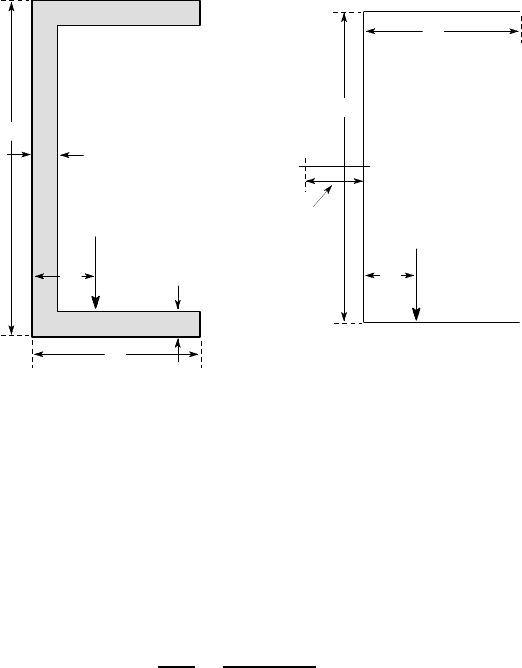
A steel beam with the channel section of Figure 6.47(a) is loaded by a shear force

of 10 kN with the line of action shown. Find the maximum shear stress and the twist

per unit length. The section has a second moment of area I

= 0.81×10

and

G= 80 GPa for steel.

10 kN

13.9

(a) (b)

Figure 6.47: (a) The channel section, (b) the mean line and location of the shear

centre

The mean line of the thin-walled section has the dimensions of Figure 6.47(b)

and the section is similar to Figure 6.26 with a = 37 mm and t = 6 mm. The ﬁrst

two steps in the above procedure can therefore be taken from Example 6.4 (§6.2).

Referring to Figure 6.28 and the associated calculations, we note that the maximum

shear stress due to an equal shear force through the shear centre occurs in the web at

the neutral axis (y= 0) and is

max

16at

9 ×10, 000

16 ×37 ×6

= 25.3 MPa.

Also, from Example 6.4, the shear centre is located at a distance

6.7 Torsion of thin-walled open sections 333

c =

= 13.9 mm

to the left of O, as shown in Figure 6.47(b).

The offset of the shear force is therefore equivalent to a clockwise torque

T = 10,000 ×(13.9 + 12) ×10

−3

= 259 Nm.

The channel section has a constant thickness t = 6 mm and perimeter

b = 37 + 74 + 37 = 148 mm,

K =

148 ×6

= 10.7 ×10

and the twist per unit length is

259

80 ×10

×10.7 ×10

−9

= 0.30 rad/m (17.3

/m).

The torque generates a maximum shear stress

259 ×10

×6

10.7 ×10

= 145 MPa,

which occurs at the edges of the wall all around the section. The maximum shear

stresses due to the shear force and the equivalent torque are shown in Figures

6.48 (a,b) respectively.

25.3 MPa

145 MPa

(a) (b)

Figure 6.48: Magnitude and location of the maximum shear stress due to (a) an equal

shear force through the shear centre and (b) the torque due to the offset of the shear

force

334 6 Shear and Torsion of Thin-walled Beams

Superposing these stress ﬁelds, it is clear that the maximum shear stress will

occur at D, where they act in the same direction, giving

max

= 25 + 145 = 170 MPa.

This example shows that the offset of the line of action of the shear force has a

dramatic effect on the behaviour of the beam in shear. It increases a modest maximum

shear stress of 25 MPa by a factor of 7 and produces an unacceptable amount of

twist per unit length for most practical applications. Thus, with open sections, it

is important to ensure that shear forces are applied as near to the shear centre as

possible. This is generally easier to achieve with symmetric sections such as I-beams,

rather than with channels, for which the shear centre lies outside the section envelope.

6.8 Summary

In this chapter, we have developed methods of estimating the shear stress distribution

in beams due to transmitted shear forces and torques. For any beam cross section,

there exists a unique point known as the shear centre, through which the shear force

must act if there is to be no twist of the beam.

When the shear force acts through the shear centre, the shear stresses are usually

small compared with the bending stresses and they can often be neglected or approx-

imated as

web

, except for built-up or welded sections or in situations where

high accuracy is required.

For thin-walled sections, the shear stress must always be parallel to the edges of

the wall. For closed sections, the shear stress is approximately uniform through the

wall thickness for all loading conditions, but for open sections, this situation arises

only when the shear force acts through the shear centre. When thin-walled open

sections are loaded away from the shear centre or in torsion, the shear stress varies

linearly through the wall thickness and the maximum shear stress and the twist may

be quite large. Furthermore, the shear centre can be located outside the envelope of

the section, making it difﬁcult to apply the load through the shear centre.

By contrast, the shear centre for closed thin-walled sections always lies within

the envelope of the section. The torsional stiffness and strength of these sections is

very easily determined with a few lines of calculation, using the results of §6.5. You

will generally ﬁnd that the section is sufﬁciently strong and stiff in torsion for the

exact location of the shear centre to be of little concern. Closed thin-walled sections

are therefore much to be preferred in design applications where signiﬁcant shear or

torsional loading is expected.