Barber J.R. Intermediate Mechanics of Materials
Подождите немного. Документ загружается.


6.4 Closed sections 315
q
B
=
V
y
A
∗
¯y
∗
I
x
+C (6.25)
and, since B can be chosen to be any point, it completely determines the shear flow
distribution except for the unknown constant C. Different values of C will give dif-
ferent but parallel lines of action for the resultant shear force V
y
, and these can be
determined using the method of §6.2. Conversely, if the line of action of V
y
is pre-
scribed, this can be used to determine C.
Thus, we see that there is a qualitative difference between the shear behaviour of
open and closed thin-walled sections. For an open section, equation (6.9) corresponds
to a unique line of action for the shear force, whereas for a closed section, equation
(6.25) with an appropriate value of the constant C describes the distribution for any
line of action of V
y
.
However, closed sections do have shear centres, in the sense of a point where
V must act in order for there to be no twist of the section. We shall return to this
question in §6.6 below.
Summary
The procedure for finding the shear flow and hence the shear stress in a thin-walled
closed section loaded by a shear force with a prescribed line of action can be sum-
marized as follows:-
(i) Choose any convenient point A as a reference point and denote the shear flow
there as q
A
=C.
(ii) Use equation (6.25) to determine general expressions for q in each segment of
the section. Remember that the area A
∗
is treated as positive if it is traversed in
passing clockwise from A to B and negative if it is traversed anticlockwise.
(iii) Equate the moment of the distribution about any convenient point to the corre-
sponding moment of the prescribed shear force and use the resulting equation to
determine the constant C.
Example 6. 5
The closed semi-circular section of Figure 6.35 is loaded by a vertical shear force V
y
,
whose line of action passes through the point O as shown. Determine the complete
distribution of shear stress in the section.
We first determine the second moment of area I
x
for the section. We can use
equation (6.13) for the semi-circular part of the section and add the contribution for
the straight part, to obtain
I
x
=
π
a
3
t
2
+
(2a)
3
t
12
= 2.237a
3
t .
It is convenient to choose the top corner of the section to be the point A, since
segments starting at A have a simple geometric shape. The shear flow in the straight
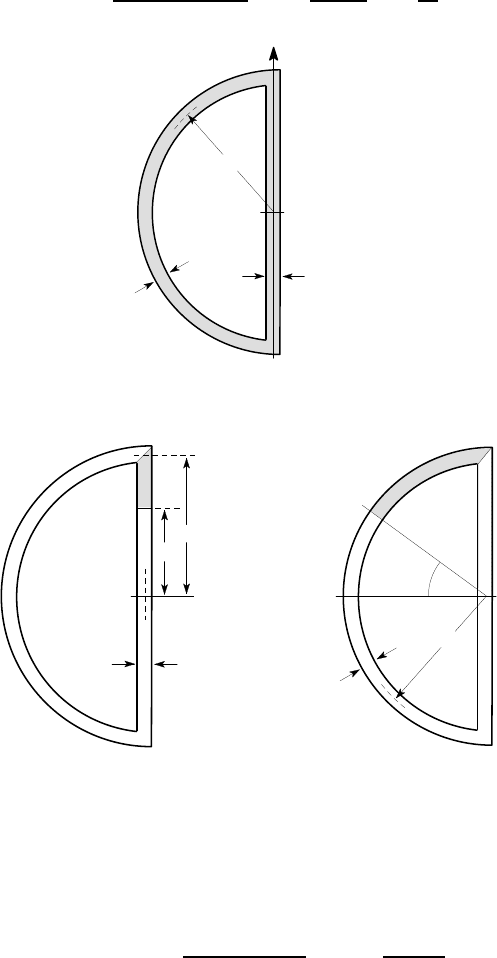
316 6 Shear and Torsion of Thin-walled Beams
portion is found from equation (6.25) by considering the shaded segment AB
1
of
Figure 6.36 (a), giving
q
B
1
=
V
y
(a −y)t(a + y)
2(2.237a
3
t)
+C =
V
y
4.474a
1 −
y
2
a
2
+C .
O
t
t
y
V
a
Figure 6.35: Closed semi-circular section
O
t
a
y
A
B
1
O
t
a
φ
A
B
2
(a) (b)
Figure 6.36
To find q in the curved portion, we use the segment shaded in Figure 6.36 (b), but
since it is traversed in passing anticlockwise from A to B, the corresponding area A
∗
must be treated as negative. We obtain
q
B
2
= −
Z
π
/2
φ
V
y
a sin(
θ
)atd
θ
2.237a
3
t
+C = −
V
y
cos
φ
2.237a
+C .
6.4 Closed sections 317
The above equations completely define the shear flow q and hence the shear
stress,
τ
= q/t, in the section, except for the unknown constant C. To determine C,
we take moments about any convenient point, as in §6.2, to enforce the condition
that the distribution is statically equivalent to the force V . The result is most easily
obtained by taking moments about O, since the moment arm is then zero for both q
B
1
and V
y
. The moment arm for q
B
2
is the radius a and we obtain
V
y
×0 =
Z
π
/2
−
π
/2
aq
B
2
(
φ
)ad
φ
= −
V
y
a
2.237
Z
π
/2
−
π
/2
cos
φ
d
φ
+
π
a
2
C
— i.e.
0 =
π
a
2
C −
2V
y
a
2.237
,
from which
C =
2V
y
2.237
π
a
= 0.285
V
y
a
.
Substituting this value back into the expressions for shear flow, we obtain
q
B
1
=
V
y
a
0.508 −0.223
y
2
a
2
; q
B
2
=
V
y
a
(0.285 −0.447 cos
φ
) ,
which completes the solution.
O
D
A
0.162
a
V
y
0.508
a
V
y
50.5
o
50.5
o
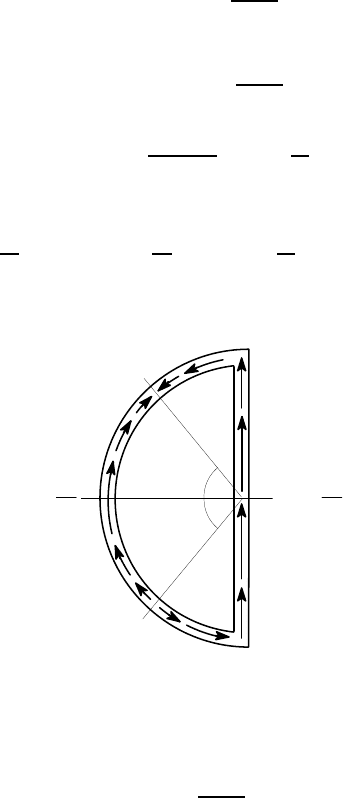
Figure 6.37: Shear stress field due to the shear force V
y
passing through O
The distribution is illustrated in Figure 6.37. Notice that the shear flow is negative
and hence clockwise in the segment −
φ
0
<
φ
<
φ
0
, where
φ
0
= cos
−1
0.285
0.447
= 50.5
o
.
The magnitude of q reaches a maximum at the two points where the section crosses
the neutral axis, being 0.508V/a at O and −0.162V/a at D.
318 6 Shear and Torsion of Thin-walled Beams
6.5 Pure torsion of cl osed thin-walled sections
For a closed section, the shear flow can be non-zero even if the shear force V is zero,
in which case equation (6.25) reduces to
q
B
= C . (6.26)
In other words the shear flow is constant around the section. This corresponds to the
case of a thin-walled closed section subjected to pure torsion.
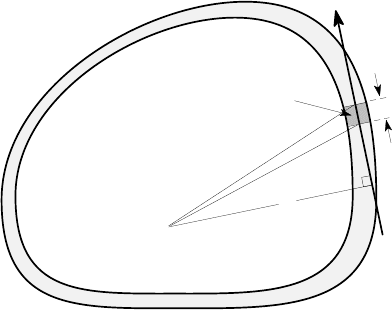
dS
dF = q dS
t dS
O
n
Figure 6.38: Calculating the torque due to a given shear flow
The torque T is the same about any point if V = 0 and we can find it by taking
moments exactly as in §§6.2, 6.4. Consider the contribution of the small element of
area tdS in Figure 6.38, where dS is an element of length around the mean line of
the section and t is the local thickness, which is not necessarily constant. The ele-
mental force associated with tdS is dF =
τ
tdS = qdS. We assume that
τ
is uniformly
distributed over tdS and hence the line of action of dF is locally tangent to the mean
line of the section — i.e. the line which is equidistant between the inner and outer
edges of the wall. The moment of dF about O is therefore ndF where n is the normal
distance from O to the local tangent to the mean line. Summing the contribution for
all such elements by integration, we have
T =
I
S
ndF =
I
S
qndS = C
I
S
ndS (6.27)
from equation (6.26). Notice that C can be taken out of the integral because it is
constant.
The final integral in (6.27) can be given a physical interpretation. From Figure
6.39 (a), we see that ndS is the product of the base and the height of the triangle OPQ
and hence is twice the area of that triangle. Summing ndS over all elements dS, we
therefore obtain twice the area A enclosed by the mean line of the section. In other
words
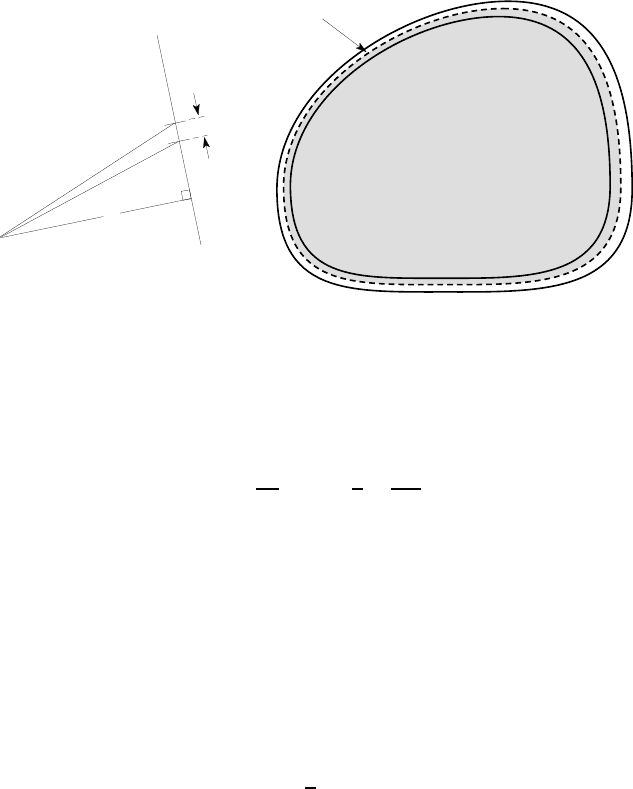
6.5 Pure torsion of closed thin-walled sections 319
I
S
ndS = 2A
and hence
T = C
I
S
ndS = 2AC . (6.28)
The mean line and the corresponding enclosed area A are illustrated in Figure
6.39 (b). Notice however that since t ≪a, only a small error would be involved in
using either the inner or the outer wall of the section to define A.
dS
O
n
P
Q
A
mean
line
(a) (b)
Figure 6.39: (a) Contribution to the integral in equation (6.27) from the element dS,
(b) Interpretation of the enclosed area A
The shear flow and shear stress can be determined from (6.26, 6.28) as
q = C =
T
2A
;
τ
=
q
t
=
T
2At
. (6.29)
Notice that the shear flow is constant around the section, but the shear stress will vary
inversely with thickness t if the latter is not constant. In particular, the maximum
shear stress will occur where the thickness t is a minimum.
6.5.1 Torsional stif fness
It is also useful to know the angle of twist
θ
, and hence the torsional stiffness of the
section. This is most conveniently found using an energy method. As in §3.3, we can
equate the work done by the torque T during loading to the stored strain energy. The
work done is
W =
1
2
T
θ
, (6.30)
since the system is elastic and the torque will be everywhere proportional to the
instantaneous angle of twist [see equation (3.30)].
320 6 Shear and Torsion of Thin-walled Beams
The stored strain energy can be obtained from equation (3.33) as
U =
1
2G
ZZZ
V
τ
2
dV , (6.31)
where V is the volume of material in the beam and we have used the relation G =
E/2(1+
ν
). The shear stress is assumed to be uniform across the thickness t and
hence is constant in the volume element dV =LtdS shown in Figure 6.40. The integral
for the strain energy can therefore be written
U =
L
2G
I
S
τ
2
tdS , (6.32)
where S is the perimeter of the closed section.
t
L t dS
dS
L
Figure 6.40: Volume element for the integration of equation (6.31)
Equating the work done and the strain energy U and using (6.29) for the shear
stress
τ
, we then obtain
1
2
T
θ
=
L
2G
I
S
T
2At
2
tdS =
T
2
L
8A
2
G
I
S
dS
t
, (6.33)
from which
θ
=
T L
4A
2
G
I
S
dS
t
=
T L
GK
, (6.34)
where
K = 4A
2
I
S
dS
t
(6.35)
is a measure of the torsional stiffness of the cross section. Notice that K has the
dimensions of length to power 4. It reduces to the polar moment of area J in the
special case where the section is axisymmetric.
In many problems, the thickness t is constant and the integral in equations (6.34,
6.35) reduces to
I
S
dS
t
=
S
t
. (6.36)
Alternatively, if the perimeter can be divided into segments S
1
,S
2
,... with thickness
t
1
,t
2
,... respectively, we have
I
S
dS
t
=
S
1
t
1
+
S
2
t
2
+ ... . (6.37)

6.5 Pure torsion of closed thin-walled sections 321
Example 6. 6
The symmetrical closed thin-walled section of Figure 6.41(a) is twisted by a torque
of 20 Nm. Find the maximum shear stress and the twist of the beam per unit length if
the material is steel (G= 80 GPa).
1
2
14
27
6.5
6.5
1
2
16.5
1
15
25
5
5
15
5
all dimensions in mm
(a) (b)
Figure 6.41: (a) A closed thin-walled section, (b) the mean line
We first determine the area enclosed by the mean line, which is
A = 5 ×15 + 5 ×15 + 5 ×15 = 225 mm
2
,
from Figure 6.41 (b). The maximum shear stress will occur where the thickness t is
a minimum (t
min
=1 mm) and hence is
τ
=
20,000
2 ×225 ×1
= 44.5 MPa.
The perimeter S of the section comprises a segment of length S
1
=5 +10+15 +10+
5=45 mm of thickness 1 mm and a segment S
2
=15+25+15 =55 mm of thickness
2 mm. We therefore have
I
S
dS
t
=
45
1
+
55
2
= 72.5
and
K =
4 ×225
2
72.5
= 2973 mm
4
,
from equation (6.35). The twist per unit length is
θ
L
=
T
GK
=
20
80 ×10
9
×2973 ×10
−12
= 0.084 rad/m .
322 6 Shear and Torsion of Thin-walled Beams
6.5.2 Design considerations in torsion
Equations (6.29, 6.34) are extremely simple and efficient to use for determining the
shear stress and twist in a thin-walled closed section loaded in torsion. In the sprit of
§1.2.2 they are therefore very useful as a design tool and there is also considerable
justification for using them ‘out of context’ to get a rough estimate of the torsional
behaviour of closed sections whose walls are not strictly thin.
Another interesting consideration here is that the torsional shear stresses are re-
duced and the stiffness increased by increasing the enclosed area A, which however
does not contribute to either the material cost or the weight of the beam. If reducing
weight and cost are primary concerns in the design, the optimal choice for torsion
is a thin-walled circular section, since this has the greatest enclosed area for a given
perimeter. For a cylinder of mean radius a and wall thickness t, the area enclosed
is A =
π
a
2
, the perimeter is S = 2
π
a and the volume of material per unit length is
V =St =2
π
at. It follows that
t =
V
2
π
a
(6.38)
and the shear stress and stiffness are respectively
τ
=
T
2
π
a
2
t
=
T
Va
(6.39)
K =
4(
π
a
2
)
2
t
2
π
a
= 2a
2
V . (6.40)
Thus, for a given material volume V , the torsional shear stress decreases inversely
with the radius a of the tube and the stiffness increases with a
2
.
Of course, there are practical reasons limiting the values of a that can be used in
particular applications. The beam has to fit into a given space and connect to other
components at the ends. Also, the thickness for given V is inverse with a from (6.38)
and for very thin sections, local buckling of the wall is a limiting failure mode. The
reader can verify this by rolling up a piece of paper, taping it to make a closed section
and then loading it in torsion. We shall discuss failure modes involving buckling in
Chapter 12.
The contribution of the enclosed area A to torsional stiffness can have some un-
expected consequences when design changes are made. In my undergraduate days,
a popular student pastime was to buy an old family saloon car and make something
more sporty by removing the roof and parts of the door surrounds. However, many of
these cars were built using ‘monocoque’ construction, in which there is no chassis.
Instead, the car body is an integral part of the structure and front and rear axle assem-
blies are attached only through local sub-frames. In this case, the torsional stiffness
between the front and rear of the car relies on the roof (and to some extent the doors)
which render the car body a closed section. Removing the roof therefore reduced
this torsional stiffness dramatically, resulting in a vehicle with quite bizarre handling
characteristics, particularly on rough roads.
It is in fact quite a challenge to obtain sufficient torsional stiffness in an open car,
even with a chassis. Closed sections can be used for the chassis members, but this

6.6 Finding the shear centre for a closed section 323
is somewhat limited by space considerations. The Lotus Seven — an inexpensive
kit car manufactured by Lotus in the 60s — solved this problem by boxing in the
transmission tunnel.
6.6 Finding the shear centre for a closed section
The energy argument of §6.5.1 can be generalized to determine the location of the
shear centre for a closed section. Remember that the shear centre is defined as the
point through which V
y
must act if there is to be no twist.
We first apply the reciprocal theorem of §3.8 to the bar subjected to the two
separate loads comprising (i) a torque T and (ii) a force V
y
acting through the shear
centre C. By the definition of C, V
y
produces no twist, so T does no work against
the deflections due to V
y
. It follows by the reciprocal theorem that V
y
does no work
against the deflections due to T and hence that during the application of T, the shear
centre does not move. Thus, the shear centre is also the centre of rotation of the
section when the beam is loaded in pure torsion.
11
Now a shear force with a more general line of action can be decomposed into
an equal force V
y
through the shear centre and a torque T = V
y
d, where d is the
perpendicular distance from C to the line of action of V
y
. With this decomposition,
the shear force acting through C will produce a displacement u
C
of C but no twist,
whereas the torque T will produce a twist
θ
of the section, but no displacement of C.
Thus, the work done when the two components are applied simultaneously is
W =
1
2
V
y
u +
1
2
T
θ
. (6.41)
In other words, there will be no coupling terms between V
y
,u and T,
θ
.
The twist
θ
due to T must be in the same direction as T and hence the second
term in equation (6.41) must be positive for all T and hence for all non-zero values
of d. But the first term is independent of d and hence W will be a minimum for a
given magnitude and direction of V
y
, if we choose the line of action of V
y
such that
d = 0. In other words, the work done by V
y
is a minimum when its line of action
passes through the shear centre. Thus, we can find the shear centre by writing the
strain energy for a shear force of general line of action, using the expression for
shear stress from equation (6.25), and requiring it to be a minimum.
From equation (6.32), we have
U =
1
2G
I
S
τ
2
tdS =
1
2G
I
S
q
2
dS
t
(6.42)
and hence
∂
U
∂
d
=
1
G
I
S
q
∂
q
∂
d
dS
t
. (6.43)
This must be zero if V
y
acts through the shear centre C.
11
Notice how these energy theorems are really quite useful!

324 6 Shear and Torsion of Thin-walled Beams
Now changing the line of action of V
y
(without changing its direction) is equiv-
alent to superposing a torque and we know from §6.5 that this merely changes q
everywhere by a constant. It follows that
∂
q
∂
d
= constant (6.44)
and this constant is non-zero (as is G), so the condition
∂
U/
∂
d =0 simplifies to
I
S
qdS
t
= 0 , (6.45)
which must be satisfied if V
y
is to act through the shear centre.
Summary
The procedure for finding the shear centre of a closed thin-walled section can there-
fore be summarized as follows:-
(i) Choose any convenient point A as a reference point and denote the shear flow
there as q
A
=C.
(ii) Use equation (6.25) to determine general expressions for q in each segment of
the section. Remember that the area A
∗
is treated as positive if it is traversed in
passing clockwise from A to B and negative if it is traversed anticlockwise.
(iii) Substitute the result into condition (6.45), which then serves as an equation for
the unknown constant C.
(iv) Substitute for C into the original expressions for q and take moments about any
point as in §6.2 for open sections, to find the line of action of V
y
, using equation
(6.18).
6.6.1 Twist due to a shear force
If the shear force V
y
does not pass act through the shear center, it will cause the
section to twist. If the location of the shear centre is known, this twist is easily found
by decomposing the shear force into an equal force through the shear centre and
an equivalent torque T =V
y
d, where d is the perpendicular distance from the shear
centre to the line of action of V
y
. In this representation, only the torque produces
twist, which is therefore given by
θ
=
T L
4A
2
G
I
S
dS
t
, (6.46)
from equation (6.34).
If the location of the shear centre is not known, a similar decomposition together
with the relation (6.45) yields a general expression for the twist of the section. We
first write the shear flow
q = q
1
+ q
2
, (6.47)
