Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

6.2 Shear centre 305

Example 6. 3

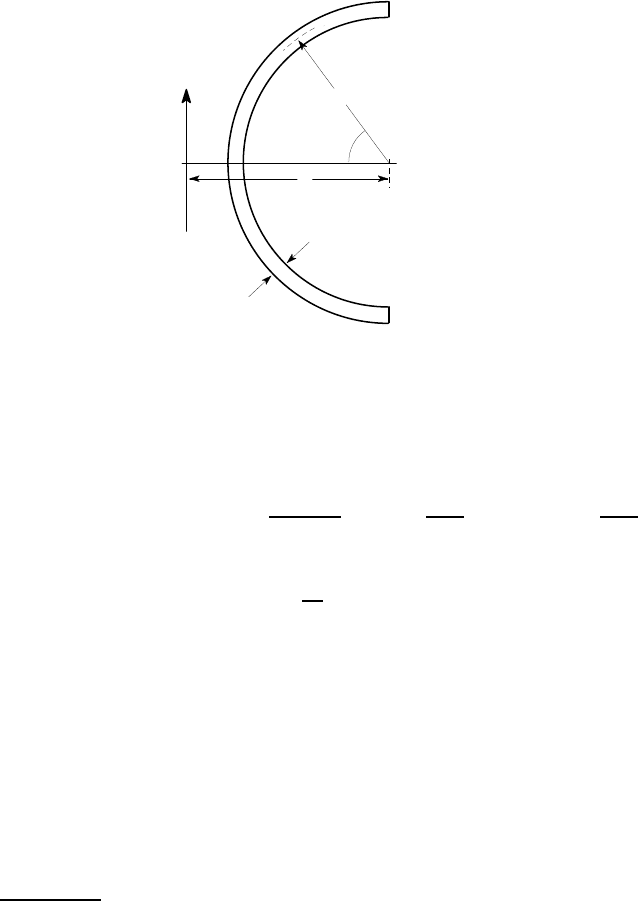
Find the distance c deﬁning the shear centre for the semi-circular section of Figure

6.23.

Figure 6.23: Location of the shear centre for the semi-circular cross section

The shear stress distribution for this section has already been determined in §6.1.4

above and is given by equation (6.15). In applying equation (6.18) to ﬁnd c, it is

convenient to take moments about the centre of the semi-circle, since the moment

arm will then be constant and equal to the radius a. We therefore have

c =

(a)

dA =

−

(a)



cos



atd

−

cos

using (6.15) and hence

c =

≈ 1.27a .

It follows that the shear centre C is actually to the left of the section, as shown

in Figure 6.23 — i.e. it is outside the semi-circle. This is surprising at ﬁrst sight,

but it is reasonable when we realize that the moment of the distribution about C has

to be zero, whereas for any point on the concave side of the section the integrand

would be everywhere positive (positive

and positive moment arm). In general, for

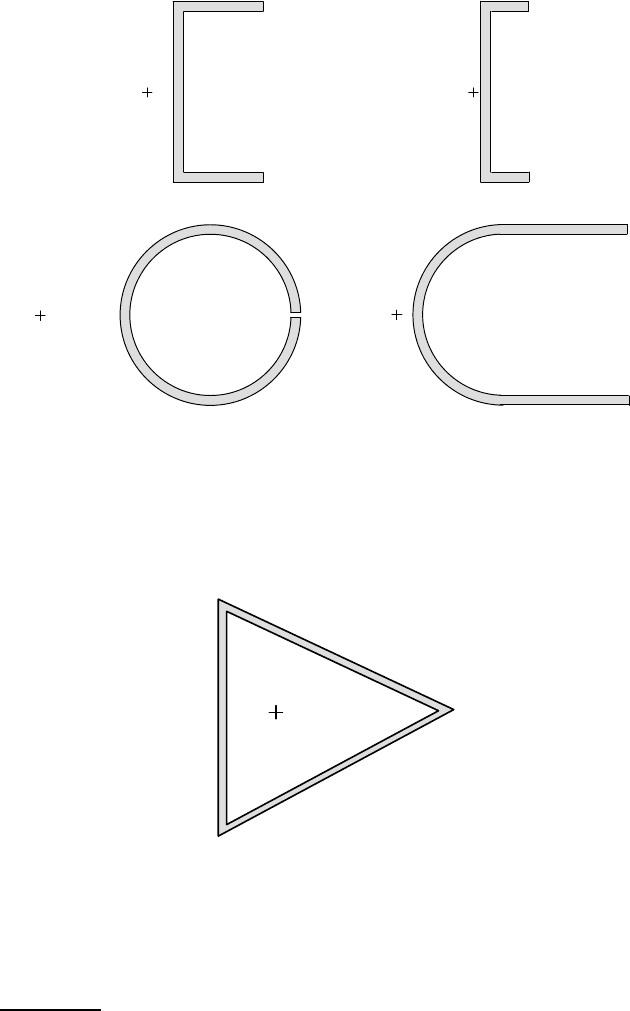
open sections such as semi-circles, channels, open box sections etc., the shear centre

is outside the section, but usually not very far outside. Some typical examples are

shown in Figure 6.24.

Notice that the sections have to be open for this to be true. A different procedure

is needed if they are closed

and generally the shear centre is then inside the section,

as shown for example in Figure 6.25. This will be discussed in §6.6 below.

A closed thin-walled section is one that completely encloses a volume. A closed section is

rendered open by a cut at any point, even if the width of the cut is inﬁnitesimal. Another

way of deﬁning this distinction is to note that a closed section is a multiply-connected

shape, whereas an open section is simply-connected.

306 6 Shear and Torsion of Thin-walled Beams

Figure 6.24: Typical shear centre locations for open sections

Thus, a major difference in shear behaviour is produced by slitting open a closed

thin-walled section. You can examine this effect by comparing a loosely rolled cylin-

drical tube of paper with the same tube after it is taped shut along the edge.

The

distinction arises because the open tube permits relative motion along the axis at the

edge, whereas the closed tube does not.

Figure 6.25: Shear centre for a closed section

Example 6. 4

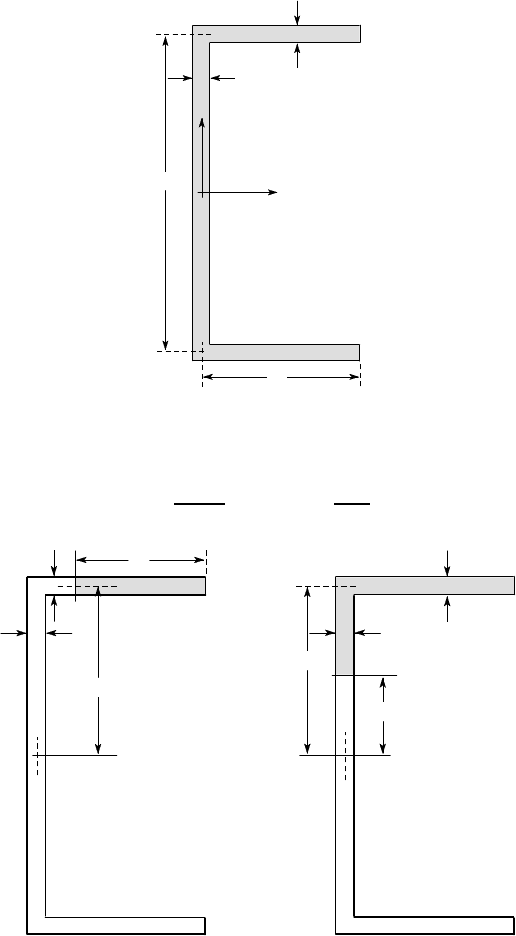
Find the location of the shear centre for the thin-walled channel section of Figure

6.26.

For a more robust experiment, compare the cardboard tube from the centre of a roll of

kitchen paper with a similar tube that has been slit along the axis, as in the third cross

section of Figure 6.24.

6.2 Shear centre 307

Figure 6.26

It is ﬁrst necessary to determine the second moment of area which is

(2a)

+ 2(at)a

cut

(a) (b)

Figure 6.27: Cuts for determining the shear stress (a) in the ﬂange and (b) in the web

If the beam is loaded by a vertical shear force V

, the horizontal shear ﬂow in the

upper ﬂange can be found using the cut of Figure 6.27 (a) and is

308 6 Shear and Torsion of Thin-walled Beams

q =

(tx)a

where x is measured from the free end as shown in the ﬁgure. An equal and opposite

stress is obtained in the lower ﬂange by symmetry.

For the web, we use the cut of Figure 6.27 (b), obtaining

∗

¯y

∗

= (at)a +

(a −y)(a + y)t

−

and hence

q =

16a



3 −



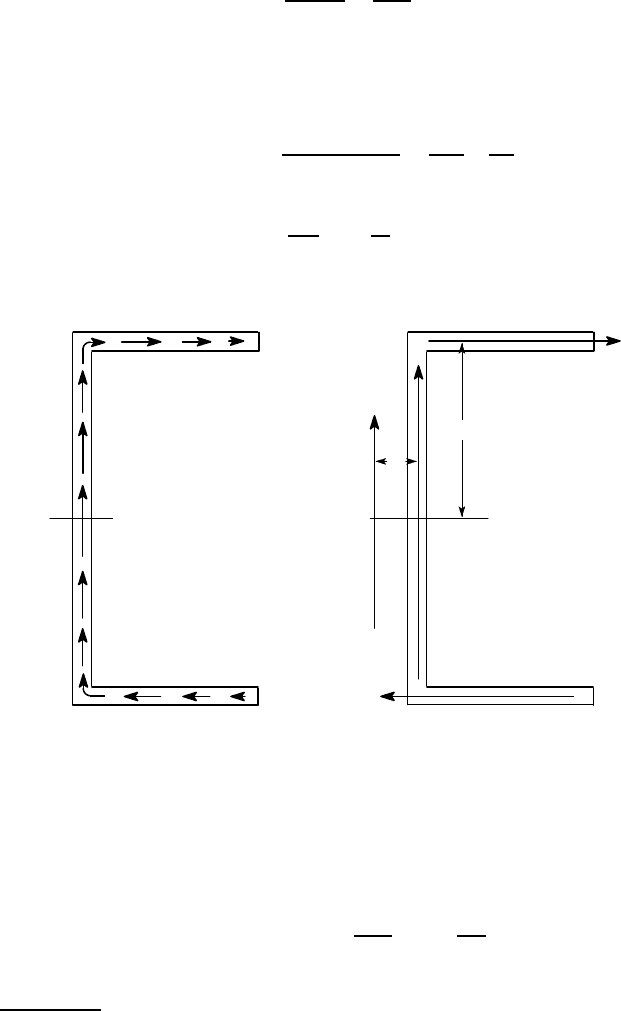
where y is measured from the neutral axis. The stress distribution is illustrated in

Figure 6.28 (a).

(a) (b)

Figure 6.28: (a) shear stress distribution in the channel section, (b) force resultants

The channel section is made up of straight segments and all the elemental forces

in any given segment will have the same line of action. We can therefore sum the

forces separately for each segment by integration. For example, the resultant of the

shear ﬂow q in the top ﬂange is

qdx =





dx =

and it has the line of action shown in Figure 6.28 (b).

Alternatively, we could make a similar cut in the lower ﬂange obtaining exactly the same

expression, except that ¯y

∗

would be −a, leading to a change of sign.

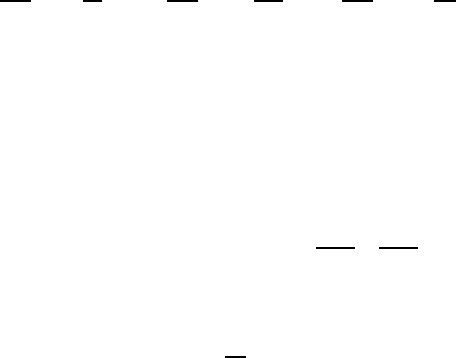
6.2 Shear centre 309

The resultant of the shear stress in the web, F

in Figure 6.28 (b), must be equal

to V

, since this is the only place where the shear stress has a vertical component. We

can conﬁrm this by evaluating F

−a

16a



3 −



dy =

16a



3y −



−a

16a



6a −



= V

The force F

in the lower ﬂange is equal and opposite to F

by symmetry, so

horizontal equilibrium is satisﬁed.

We can now determine the location of the shear centre by taking moments about

the point O in Figure 6.28 (b). The force V

is statically equivalent to the system of

forces F

and hence must have the same moment as this system about any

point. It follows that

×c = F

×a + F

×0 + F

×a =

and hence

c =

Notice that by taking moments about O, we were able to make the moment arm

for F

equal to zero. If we had recognized this from the beginning, we could have

avoided calculating the shear stress in the web, thereby shortening the calculation.

In general, when the problem asks only for the location of the shear centre, a careful

choice of the point about which to take moments can often result in a saving of

algebraic work.

Experiment

It is difﬁcult to load a channel section at the shear centre, since the latter occurs

outside the section. It is easier to load it on the ﬂange. This is equivalent to superpos-

ing a moment in the clockwise sense, as shown in Figure 6.29, and it will twist the

section. You can test this experimentally by making a channel section beam from a

piece of thin metal plate, ﬁxing it at one end and loading the other end by a transverse

force, as in Figure 6.29 (a). You will ﬁnd that the free end rotates clockwise under

the action of the equivalent moment of Figure 6.29 (b).

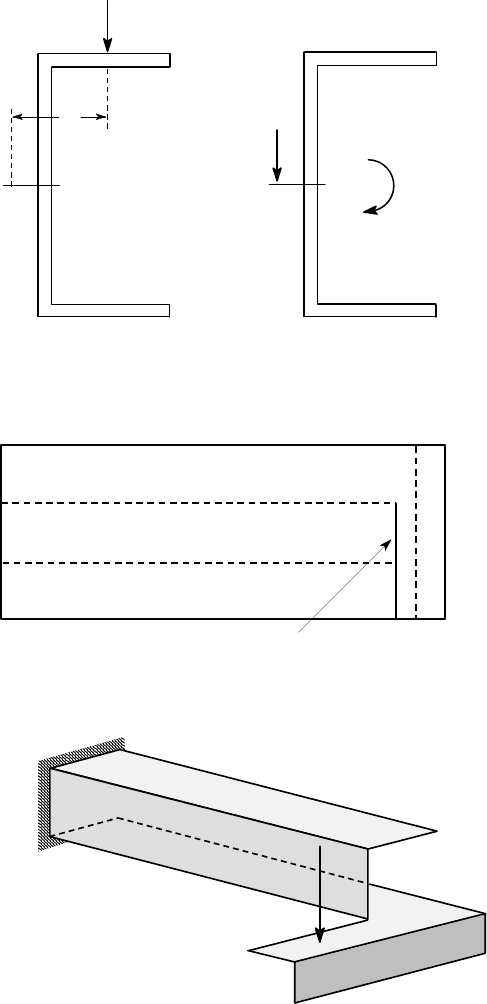
As a variant on this experiment, cut out a rectangular plate as in Figure 6.30 (a)

and fold it along the dotted lines to form the beam of Figure 6.30 (b). You will then

be able to investigate the effect of loading outside the envelope of the section and in

particular to locate the shear centre by ﬁnding the line of action of the force F for

which there is no twist.

310 6 Shear and Torsion of Thin-walled Beams

T = Fd

(a) (b)

Figure 6.29: (a) shear loading of the channel section, (b) equivalent loading system

with the force acting through the shear centre and a torque

cut

Figure 6.30(a): An experimental model for ﬁnding the shear centre of a channel

section

Figure 6.30(b): Fold the plate to form the channel-shaped cantilever shown and ex-

plore the effect of the line of action of F on the twist of the section.

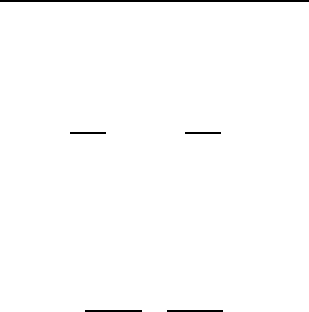
6.3 Unsymmetrical sections 311

6.3 Unsymmetrical sections

So far, we have considered only sections with at least one axis of symmetry. The

generalization to unsymmetrical sections is routine, but leads to signiﬁcantly more

complicated algebra. The principal reason for performing these calculations is to de-

termine the location of the shear centre, since the moment resulting from shear load-

ing of an open section away from its shear centre [see e.g. Figure 6.29 (b)] can cause

signiﬁcant torsional stresses and twist, as will be discussed in §6.7 below. By con-

trast, the shear stresses associated with shear loading acting through the shear centre

are often sufﬁciently small to be neglected, or estimated by simple approximations

as discussed in §6.1.2.

6.3.1 Shear stress for an unsymmetrical section

The derivation of §6.1 can be generalized to unsymmetrical sections, using equation

(4.20) in place of (6.2) to deﬁne the bending stress. We obtain

q =

t =

−V

∗

¯x

∗

−(V

−V

∗

¯y

∗

−I

)

, (6.19)

where (¯x

∗

, ¯y

∗

) are the coordinates of the centroid of A

∗

relative to the centroid of the

whole section and we have used the relations

= −

; V

, (6.20)

obtained by similar arguments to equation (6.1), using the sign convention of Figures

4.1, 6.1.

If the coordinate system Oxy is chosen to coincide with the principal axis system

as in §4.4.3, the product inertia I

will be zero and equation (6.19) reduces to

q =

t =

∗

¯x

∗

¯y

∗

, (6.21)

which is of course equivalent to the superposition of two applications of equation

(6.9) about orthogonal axes.

6.3.2 Determining the shear centre

Suppose that the shear centre of the unsymmetrical thin-walled section of Figure

6.31 is at the point C(a, b). As before, the shear ﬂow q deﬁned by equation (6.19)

corresponds to an elemental force dF =

tdS = qdS. The moment of the complete

stress distribution about O can then be equated to the moment of the two shear force

components V

, giving

−bV

nqdS . (6.22)

312 6 Shear and Torsion of Thin-walled Beams

For a particular problem, q will be known from (6.19) and can be substituted

into (6.22). When the integral is evaluated, the coordinates a,b of the shear centre

can be determined by equating coefﬁcients of V

. Alternatively, we can solve two

separate problems — one with V

= 0 to determine a and another with V

= 0 to

determine b.

Figure 6.31: Determining the shear centre for an unsymmetric section

The procedure is algebraically tedious and will not be pursued here. More details

and worked examples can be found in Cook and Young §9.8 or Bickford §4.4.

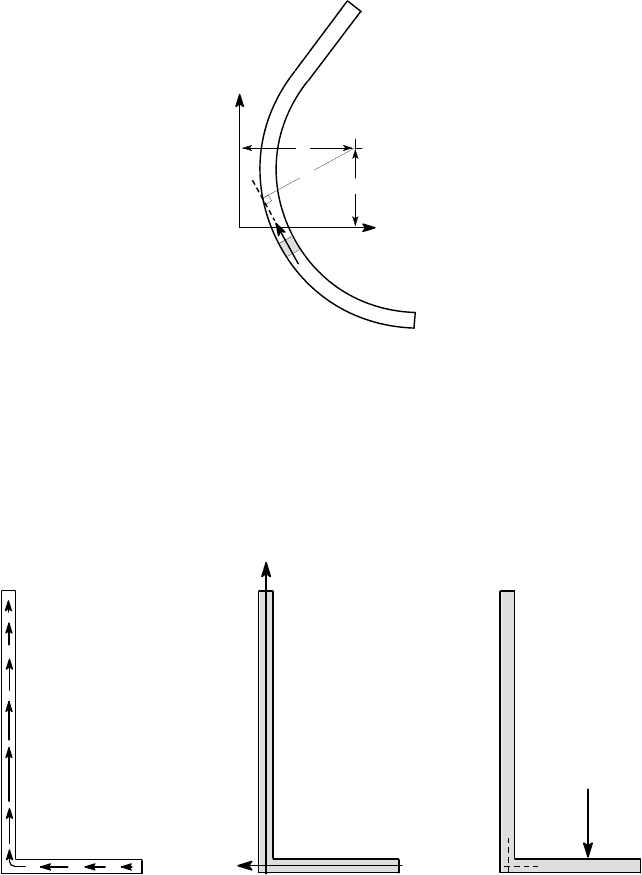
Shear centre for angle sections

One example for which the determination of the shear centre is very straightforward

is the thin-walled angle section of Figure 6.32.

(a) (b) (c)

Figure 6.32: (a) Shear stress distribution, (b) equivalent forces and shear centre

location for an angle section, (c) loading by a force on the ﬂange

6.4 Closed sections 313

The shear stress distribution has to follow the walls of the section as in Figure

6.32 (a) and hence is equivalent to the two forces F

shown in Figure 6.32 (b).

The resultant of these two forces must act through the corner of the section C which

is therefore the shear centre.

Loading of an angle by a shear force on the lower ﬂange, as shown in Figure

6.32 (c), will therefore lead to clockwise twist of the section. Notice incidentally that

vertical loading as in Figure 6.32 (c) implies that F

= 0 and hence that the shear

stress in Figure 6.32 (a) changes direction at some point in the horizontal leg.

6.4 Clo sed sections

A closed section is one with one or more enclosed cavities. Another way of de-

scribing it is to say that a single longitudinal cut through the wall will not generally

separate the section into two parts, but will simply render the section open, as in the

case of the slit tube of Figure 6.33 (b).

(a) (b)

Figure 6.33: (a) Closed section and (b) equivalent open section obtained by slitting

the closed section along the axis

In this section, we shall restrict attention to the case of a single enclosed cav-

ity — e.g. a cylindrical tube or a box section. Other sections with several cavities

(i.e. a closed section with continuous internal stiffeners) can be treated by similar

methods.

6.4.1 Determination of the shear stress distribution

Suppose we have an arbitrary closed thin-walled section transmitting a shear force

. We follow the same procedure as in §6.1, but in order to remove a piece of the

See §6.6.2 below.

314 6 Shear and Torsion of Thin-walled Beams

section to write an equilibrium equation, we now have to make two cuts — e.g. one

at A and one at B in Figure 6.34 (a). We shall adopt the convention that

is positive

in the anticlockwise sense, as shown, remembering that because of the thinness of

the wall, the stress is constrained to be parallel to the wall at every point.

q ,

δz

(a) (b)

Figure 6.34: (a) Cuts needed to determine the shear stress for a closed section, (b)

section removed by the cut

The section removed by the cut is shown in Figure 6.34 (b). Notice that with the

anticlockwise positive convention for

, the shear stresses complementary to

act in opposite directions along the axis on the cut surfaces. The resultant longitudinal

shear force on the two cuts is therefore

Q =

z −

z = (q

−q

)

and substitution into equation (6.7) yields

∗

¯y

∗

+ q

. (6.23)

In using this result, it is important to adhere to the convention of Figure 6.34 (a) that

∗

is that part of the section traversed in passing clockwise from A to B. However,

∗

¯y

∗

for the complete section (shaded + unshaded) is zero and hence

∗

¯y

∗

)

shaded

= −(A

∗

¯y

∗

)

unshaded

. (6.24)

It follows that we can pass in the anticlockwise direction from A to B, provided the

area traversed A

∗

is treated as negative in equation (6.23).

Equation (6.23) deﬁnes the shear ﬂow q throughout the section except for an

arbitrary additive constant. Suppose we choose an arbitrary ﬁxed point A and write

=C, where C is unknown. Equation (6.23) then takes the form