Barnes D.J., Chu D. Introduction to Modeling for Biosciences

Подождите немного. Документ загружается.

4.5 Chemical Reactions 173

remaining agnostic about the speciﬁc value of h. This leads us to a system of two

differential equations.

˙y =−v

max

˙z = v

max

(4.44)

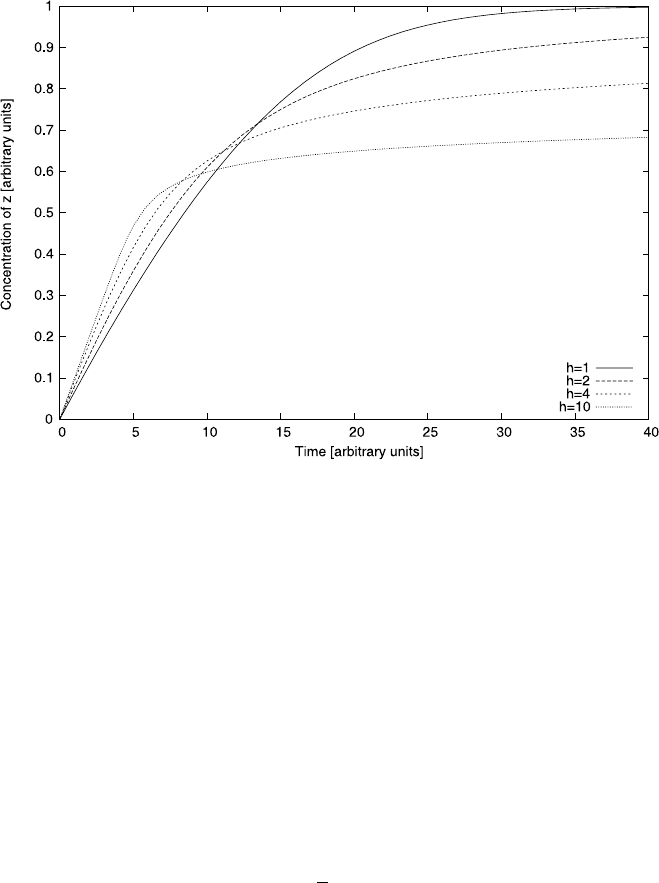
Figure 4.16 plots some solutions for this system assuming initial conditions of

y(0) =1 and z(0) =0. A salient feature of the graph is that the MM-kinetics leads

to initially slower growth. Yet, within the time period shown in the plot it clearly

leads to the highest total conversion. Initial growth is highest for the highest Hill

coefﬁcient (i.e., h =10) shown in the plot, but this one also shows the poorest total

amount of converted substrate after the considered time period.

This qualitative behavior can be easily explained from the properties of the

MM/Hill kinetics. Hill functions become increasingly step-like as h increases (see

Fig. 4.15). For our system, this means that initially, when the substrate concentration

is at its maximum, Hill functions with a high h are much closer to their saturation

value of 1; the MM function, on the other hand, will be comparatively low, resulting

in a lower initial conversion rate. However, as the substrate is depleted and the con-

centration of y falls below y = K, a system with a higher Hill coefﬁcient will see

the conversion rate drop to zero much more quickly. The MM-function, however,

is much less step like and relatively efﬁcient conversion continues even if y is well

below K.

4.15 Formulate the system of differential equations corresponding to (4.44)but

under the assumption that y(t) is replenished at a constant rate.

4.16 What happens qualitatively to the solution of the system (4.44) for very small

and very large values of K. Conﬁrm your conjectures by explicit numerical solu-

tions?

4.17 What happens to the solution of the system (4.44) when t →∞?

4.18 For the system (4.44), plot the conversion rate as a function of time.

4.5.2 Modeling Gene Expression

Enzyme kinetics is an important aspect of biological process modeling. Beyond that,

Hill dynamics is also commonly used to model transcription-factor (TF) regulated

gene expression. As in the case of enzyme kinetics, the use of the MM/Hill function

to describe the regulation of genes relies on the assumption of a separation of time-

scales. We need to assume that binding of TFs to and from the operator site happens

174 4 Differential Equations

Fig. 4.16 A numerical solution for the differential equation (4.44)forv

max

= 1, K = 0.1and

x = 0.1. Note that for higher Hill coefﬁcients it takes longer for the substrate to be used up

much faster than expression of gene products. Generally, this assumption is true. We

will later explicitly derive the Hill equation for gene expression (see Sect. 6.2.2).

For the moment, we have to ask the reader to invest faith in the correctness of our

assertions.

Assume that we have a single gene that is expressed into a product x at a rate a.

To make the model somewhat meaningful, we have to assume that the product is

broken down with a rate b to avoid trivial and unrealistic unbounded growth rates

of the concentration of the product. We have already formulated this differential

equation above.

˙x =a −bx (4.19)

We also have found the general solution to this system.

x(t) =

+Ce

−bt

(4.20)

This is satisfactory as a very simple model of an unregulated gene. It does not cap-

ture the more important case of a regulated gene. In order to model regulated genes,

we need to extend the model to include the action of a TF Y (that is present with a

concentration y) on the rate of gene expression.

To begin with, let us assume that the promoter of G

, the gene encoding pro-

tein X, is controlled by a single binding site for the TF Y which binds to its binding

site with a rate constant of k

and dissociates with a constant k

off

. For the moment,

4.5 Chemical Reactions 175

let us also assume that Y is an activator. The gene G

will then operate in two pos-

sible regimes, depending on whether Y is bound or not. If it is bound, then it will

express X at a high rate a

; otherwise it will only express Y at a “leak” rate a

where a

. Both cases can be described separately by a differential equation

of the form of (4.19). If we know the probability P

(y) that the TF is bound to its

binding site, then we can combine the two differential equations into one.

˙x =(1 −P

(y))a

(y)a

−bx

= a

(y)(a

−a

) −bx

The ﬁrst line just expresses the intuition that if the TF is bound to the operator site

with a probability of P

(y) then the gene will express at a high rate for exactly

this proportion of time. The second line is only a rearrangement of the terms on

the ﬁrst line. The question we need to answer now is how we can express P

(y)

mathematically. As it turns out, the MM function can be used to approximate this

probability.

(y) =

y +K

if K =

off

In this case, the MM-constant K is deﬁned by the ratio of the unbinding rate and

binding rate of the TF to its operator site. Altogether we thus obtain a differential

equation describing the expression of a protein from a gene.

˙x =α +β

y +K

−bx (4.45)

Here we renamed a

and a

−a

to α and β respectively, for reasons of notational

simplicity. While we have not derived this expression from ﬁrst principles, at least

for extreme parameters it seems to make sense. For example, if we assume that

the TF exists in an inﬁnite concentration y, then Y is continuously bound to the

operator site. In this case the expression rate will be α +β. However, particularly

for smaller K, the actual expression rate will be close to this value even for y<∞.

In reality, the fraction of time the TF is bound to its operator site will always be

slightly below one, but probably by not very much. Clearly, the higher the binding

rate k

of Y to its operator site in relation to the unbinding rate, the smaller is K

and (near) continuous occupation of the binding site can be achieved by lower TF

concentrations.

4.19 Write down and solve numerically the full “unpacked” system of differential

equations corresponding to (4.45), i.e., write out the system of differential equa-

tions for which the MM/Hill function is an approximation. Explore its dynamics

and compare it to the solutions to (4.45).

In many cases a particular operator site has more than one binding site for a

particular TF. Modeling these cases can be somewhat more intricate when each

of the possible occupation conﬁgurations of the binding sites is associated with

176 4 Differential Equations

a different expression rate. To consider a simple case, assume that we have two

binding sites and that there are only two possible expression rates, namely, the leak

rate when zero or one of the binding sites are occupied, and a high rate if both

are occupied. Remembering that the MM-function formulates the probability of a

single binding site being occupied, we can now write down the rate equation for our

system.

˙x =α +β

(y +K)

−bx (4.46)

The high expression rate is only relevant when all N binding sites are occupied,

which happens with a probability of

(y+K)

; otherwise the gene is expressed at the

leak rate. While mathematically correct, this form of the kinetic equation is rather

unusual and instead the gene activation function in the presence of several binding

sites of a TF is more often assumed to be of the Hill form.

˙x =α +β

−bx

Similar to the case of enzyme kinetics, the Hill coefﬁcient is normally measured

rather than derived from ﬁrst principles and the Hill coefﬁcient carries some infor-

mation about the cooperativity between the binding dynamics of the underlying TF

binding sites. If the TF is a monomer and it occupies N different binding sites on

the operator, then h ≤ N . The Hill coefﬁcient h will reach its maximum h = N in

the case when there is perfect cooperativity between the sites. This means that the

DNA-TF compound is unstable unless all binding sites are occupied. In this case,

binding can only happen if N TF bind to the N binding sites simultaneously, or

at least within a very short window of time. Perfect cooperativity of this kind is

primarily a mathematical limiting case and in practice there will be imperfect co-

operativity. This means that there will be a ﬁnite (but probably small) stability of

the DNA-nucleotide compound even if only some of the N binding sites are occu-

pied. The maximum binding times will only be achieved when all binding sites are

occupied. In these cases the Hill coefﬁcient will be smaller than N.

Often, TFs are themselves not monomers but dimers or higher order compounds.

In this case, if the Hill function is formulated in terms of the concentration of the

monomer form of the TF, then h could be higher than the number of binding sites.

So far we have assumed that the TF is an activator; there is also a commonly used

gene activation function for repressors, that is if the gene G

is repressed by the TF

species Y .

˙x =α +β

−bx

The Hill repressor function is simply 1−h(x) and thus shares the general qualitative

features of the original function. Gene expression is highest when the concentration

of the repressor y = 0; for very high concentrations of the repressor there is only

leak expression activity α.

4.6 Case Study: Cherry and Adler’s Bistable Switch 177

Gene activation functions can be extended to describe a gene being regulated

by multiple TFs. This is generally not difﬁcult, but care must be taken to properly

describe how the interaction between the TFs works. For example, if we have two

repressor species Y

and Y

and both can independently down-regulate gene expres-

sion, then the following differential equation would be a possible way to capture the

behavior.

˙x =α +β

−bx

Alternatively, if Y

and Y

only partially repress the expression of the gene, then it

would be more appropriate to describe the gene activation function as a sum of two

Hill repressors.

˙x =α +β

+β

−bx

The speciﬁc function used will depend on the particular biological context of the

system that is to be modeled.

4.20 Write down an activation function for a gene that is activated by Y

but re-

pressed by Y

. Formulate the various possibilities for how the repressor and the

activator can interact.

4.21 Formulate the gene activation function for the above case when the activator

and the repressor share the same binding site (competitive binding).

4.6 Case Study: Cherry and Adler’s Bistable Switch

Let us now look at an example to illustrate some of the ideas we have developed.

A relatively simple yet dynamically very interesting example is the bistable genetic

switch that was ﬁrst described by Cherry and Adler [8]. The system consists of

two genes that repress one another via their products. Let us assume the ﬁrst gene

produces a protein X that represses the expression of gene G

producing Y .

Similarly, Y itself also represses the expression of G

. We can immediately write

down the differential equations describing the system.

˙x =

−bx

˙y =

−by

(4.47)

Here we make the special assumption that the system is symmetric in the sense that

the gene activation function of both genes has the same parameters K and h and

that both products are degraded at the same rate b.

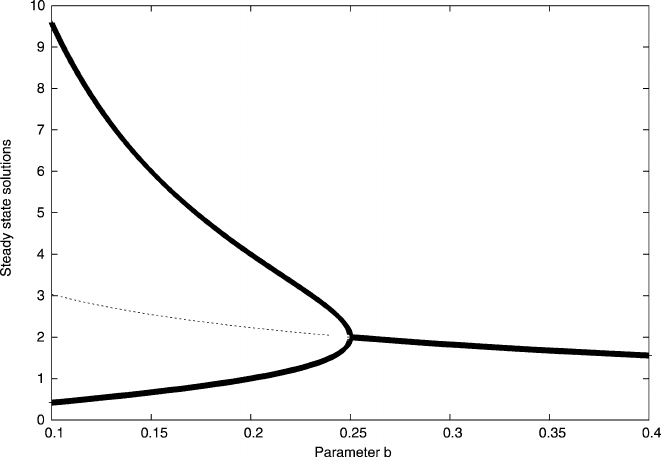
178 4 Differential Equations

Fig. 4.17 The solutions for the system of two mutually repressing genes as deﬁned in (4.47). We

keep K =2 and vary the parameter b

The system is too complicated to be solved analytically and it is necessary to

ﬁnd the solutions numerically. Given the inherent symmetry of the system, that is

and G

are dynamically identical, we would expect that the solutions for x and

y are always the same. As it will turn out though, for some parameters of the system,

x and y can have different steady state solutions. Figure 4.17 plots the steady state

solutions of the system for a particular choice of parameters. Normally, we would

have to specify which variables we consider but, in the present case, this is not nec-

essary; the symmetry of the model means that x and y are always interchangeable,

which does not mean that their values are always equal. In Fig. 4.17 the vertical

axis records the possible steady state values as the parameter b is varied (always

assuming a ﬁxed K = 2).

At the high end of b the system apparently allows a single solution only. Since

we have two variables, but only one possible solution, this must mean that in this

area x

∗

= y

∗

.Atb<0.25 the single steady state splits into three solutions. The

dashed line are steady state solutions where x

∗

; as it will turn out, these

solutions are unstable solutions and we would not expect them to be observed in

a real system. Any tiny ﬂuctuation away from this steady state would lead to the

system approaching one of the other solutions.

The stable solutions s

and s

of the system correspond to the top and bottom

(thick) lines. In this area, if one of the variables, say x, takes the steady state x

∗

then y will take the other stable state y

∗

= s

. Yet both steady states are possible

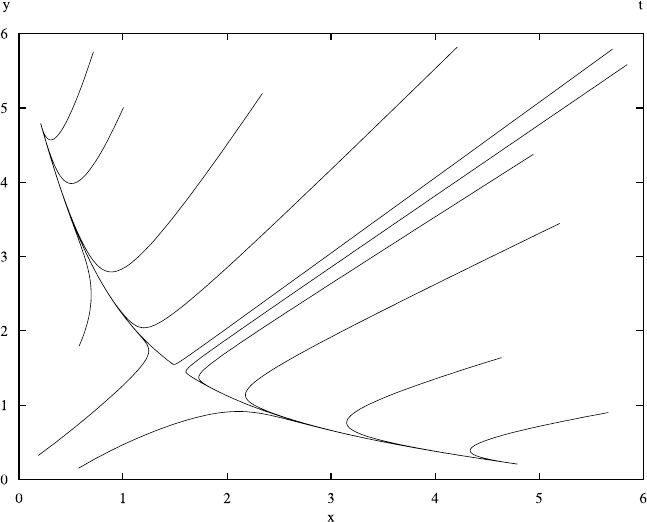
4.6 Case Study: Cherry and Adler’s Bistable Switch 179

Fig. 4.18 The phase-space representation of solutions for (4.47). The parameters are K =2and

b = 0.2. The horizontal axis represents x and the vertical axis represents y. Each line corresponds

to a trajectory of the system starting from an initial condition. Depending on the initial condition,

the system ends up in one of the two steady states. Compare this with the solutions plotted in

Fig. 4.17

for both variables. Which one is taken depends exclusively on the initial conditions

of the system.

Biologically this can be easily understood. If, say, G

is expressed at a high

rate, then this means that the concentration of X is high in the cell. Since X is

repressing Y , this also implies that the gene G

will not be expressed at a high rate,

but is repressed. Intuitively, one can thus easily understand how the symmetry of the

system is compatible with the products having two different steady states. However,

note that whether or not X or Y is expressed at a high rate will depend on the initial

conditions of the system. If we start with a high concentration of X then we would

expect that Y is suppressed and that the system remains in this steady state. On the

other hand, if we start with Y initially being higher, the system will remember that

and remain in a steady state deﬁned by a low concentration of X.Thisisalsohow

we need to read the results in Fig. 4.17.

The dependence of the steady state on the initial conditions is illustrated in

Figs. 4.18 and 4.19. Figure 4.18 shows solutions for the differential equations in

phase space. The phase space shows x versus y; each point on each of the lines

in this diagram corresponds to a particular time. The various curves in this ﬁgure

180 4 Differential Equations

Fig. 4.19 Some sample solutions of (4.47) for different initial conditions. The parameters are

K =2andb = 0.2 and we keep y(0) =2. If x(0)>y(0) then it assumes the higher steady state,

otherwise the lower. Compare this with Figs. 4.17 and 4.18

represent trajectories of the system that starts at some point and then move to one

of the steady states. The sample curves in this phase space diagram show a clear

partition of the space into two halves. The curves that originate above the diagonal

deﬁned by x =y end up in the steady state in the upper right corner of the ﬁgure.

This steady state corresponds to G

suppressing G

or a high concentration of Y

and a low concentration of X. Trajectories that start below the diagonal end up in a

steady state where G

represses G

It is instructive to compare this phase-space representation with the normal time

solutions of x(t) showninFig.4.19. In all curves in this ﬁgure we kept y(0) = 2.

Depending on the initial conditions, the variable x(t) tends to the high steady state,

when x(0)>y(0) and to the low state otherwise. The graph does not show y(t),

which would take the steady state x does not take.

Let us now obtain another perspective on the system and consider the stability

properties of the steady state solutions. Based on our numerical examples, we would

expect that the steady state x

∗

is only stable when it is the only solution. If the

parameters allow another stable state x

∗

=y

∗

then we expect that one to be stable.

To ascertain this we ﬁrst need to calculate the Jacobian.

J =

⎡

⎣

−b −

)

−

)

−b

⎤

⎦

(4.48)

4.6 Case Study: Cherry and Adler’s Bistable Switch 181

Let us now analyze the stability of the system using the same parameters as in

Fig. 4.19. We have calculated that this particular choice allows two stable steady

states which we (arbitrarily) assign to x

∗

= 4 and y

∗

= 1 (we could have done

this the other way around as well); Fig. 4.19 shows how these steady states are

approached. To obtain the stability of the ﬁrst steady state, we need to set in the

values of x

∗

= 4 and y

∗

= 1 along with the parameter values K = 2 and b = 0.2.

Calculating the eigenvalues of the resulting matrix then gives: e

=−0.04 and e

−0.36. Both eigenvalues are negative, which conﬁrms that the steady state is stable.

The second steady state where X is repressed gives the same result, as we would

expect.

We still need to check the stability of the steady state given by x

∗

= y

∗

2.229494219. Again, substitution of this value into the Jacobian and calculating the

eigenvalues yields e

≈0.02164 and e

≈−0.42164. Since one of the eigenvalues

is positive, this conﬁrms that the steady state is unstable, as suspected.

In this particular case of a system consisting of two differential equations only,

there is another way to represent the behavior of the system. The nullclines are the

curves obtained by individually setting the expressions on the right hand sides of

the differential equation (4.47) to zero. They essentially show the possible steady

states for each of the two equations separately; the actual steady states are at the

intersections of the nullclines.

x =

b(K

)

x = K



1 −by



Figure 4.20 plots these curves for the particular case of K = 2 and b = 0.2. The

three possible positive and real steady states correspond to intersection points of

the nullclines. From a computational point of view, it is often much easier to plot

the nullclines rather than to explicitly solve the equations to obtain the steady state.

Furthermore, the nullcline equations can also provide a better intuition as to which

parameters inﬂuence the number and location of steady states.

4.22 Formulate the differential equation for a self-activating gene, that is a gene

whose product activates its own expression. Assume that the gene product is broken

down at a rate of b. Write down the differential equation and analyze the number of

steady states.

4.23 Formulate the system of differential equations for the import of a nutrient S

that exists in the environment at a concentration s by a gram-positive bacterium.

Assume that it is taken up through porins into the periplasm ﬁrst and then into the

cytoplasm by different porins. Assume that uptake by porins obeys Hill-dynamics.

Explore different model assumptions, including that ˙s =0.

4.24 Use the previous model, and vary the volume of the periplasm and the cyto-

plasm. What are the effects?

182 4 Differential Equations

Fig. 4.20 The nullclines for the system in (4.47). The parameters are K = 2andb = 0.2. The

horizontal axis represents x and the vertical axis represents y. The intersections between the lines

represent steady states. Compare this with the solutions plotted in Fig. 4.17

4.7 Summary

Differential equations are powerful tools in biological modeling. In this chapter we

have refreshed the reader’s understanding of the basic ideas of differential calculus.

We have also introduced some basic methods of solving the differential equations.

The material presented here necessarily barely scratches the surface of the body of

available knowledge, yet we believe that it should be sufﬁcient to help in formu-

lating a number of biologically interesting models. Eventually, however, the reader

may wish to consider deepening her knowledge of the subject by consulting more

specialist volumes.