Barnes D.J., Chu D. Introduction to Modeling for Biosciences

Подождите немного. Документ загружается.

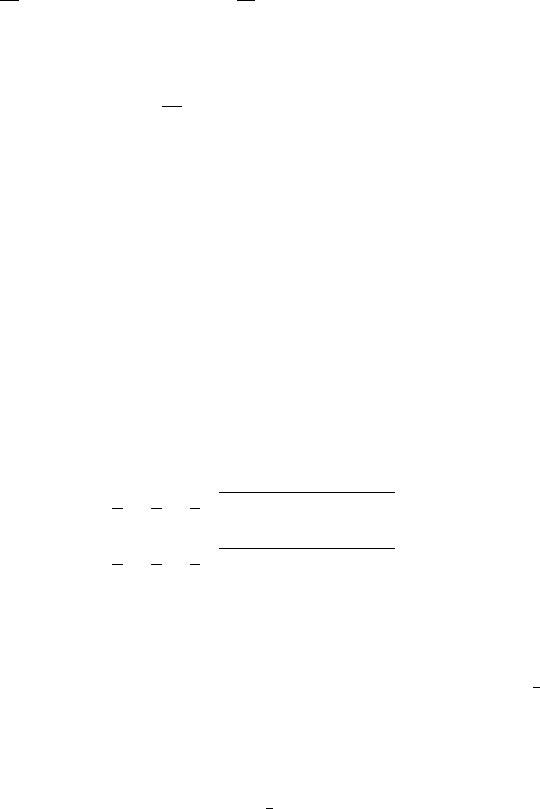
4.4 Case Study: Malaria 163

real parts of the eigenvalues. These can be directly used to classify the stability of

any steady state according to the following two rules.

• If the real parts of all eigenvalues in J(x

∗

) are negative, then x

∗

is stable.

• If at least one eigenvalue in J(x

∗

) is positive, then x

∗

is not stable.

With this new tool in hand, let us analyze the stability of the Malaria model (4.30)

above. Remember that the model was given by

s =a

(

1 −s

)

m −bs,

m =c

(

1 −m

)

s −dm (4.30)

In the Jacobian matrix, the top left entry of the matrix is given by

1,1

∂

∂s

(

a(1 −s)m −bs

)

Following (4.36), the full Jacobian of the system will be:

J(s, m) =



−am −ba

(

1 −s

)

(

1 −m

)

−cs −d



(4.38)

We wish to evaluate the stability of the steady state m

∗

= s

∗

= 0; so we need to

determine the Jacobian at this point.

J(s

∗

) =



−ba

c −d



(4.39)

Using a computer algebra system, we can now determine the eigenvalues of this

matrix and obtain:

=−

−



−2 db +b

+4ca

=−

−



−2 db +b

+4ca

To illustrate the stability of the eigenvalues we must choose speciﬁc parameters

values. Figure 4.11 plots the eigenvalues for the various values of b while keeping

a = 1, c = 1 and d = 2. This is the parameter choice corresponding to Fig. 4.10.

The steady state analysis predicts the existence of a negative steady state if b>

which, however, the system does not seem to approach when we choose positive

initial conditions (luckily). After performing our elementary stability analysis, we

can now explain why not.

Figure 4.11 shows that one of the eigenvalues is positive which means that the

steady state m

∗

= s

∗

= 0 is unstable for b<

. Introducing a small disturbance

will lead to the system moving away from this steady state; hence for this range of

parameters the system will approach the positive steady state. On the other hand, for

164 4 Differential Equations

Fig. 4.11 The eigenvalues of model (4.30) at the steady state s

∗

=0. We used the parame-

ters, a = 1, c = 1, d =2 and we varied b.Forb<0.5 the steady state is unstable, but it is stable

for b>0.5

,Fig.4.11 shows that both eigenvalues are negative, and hence the steady state

is stable. This means that, even after “small disturbances”, the system will revert to

the steady state of m

∗

=0. Incidentally, such small disturbances could, in fact,

be quite large. As we see in Fig. 4.10, if we start from s

=−1ors

= 1, in both

cases, the system reverts to a state where there is no infection.

The stability of the steady state is, in essence, the reason why we need not worry

about our system approaching a negative steady state, as long as we start from pos-

itive initial conditions. A trivial stable steady state is an attractor for all trajectories

starting from positive initial conditions; once at the stable steady state, there is no

more escape from it.

We have now established that for the parameters a = c =1 and d = 2 there is

a stable steady state corresponding to s = m = 0 when b>

. This steady state

is unstable when 0 <b<

. This suggests that, in this case, the other, non-trivial

steady state is in fact the stable one. We can conﬁrm this using our Jacobian. What

we are interested in is the Jacobian at the steady state that we have calculated earlier

for the system.

∗

ca −db

c(a +b)

∗

ca −db

a(c +d)

(4.31)

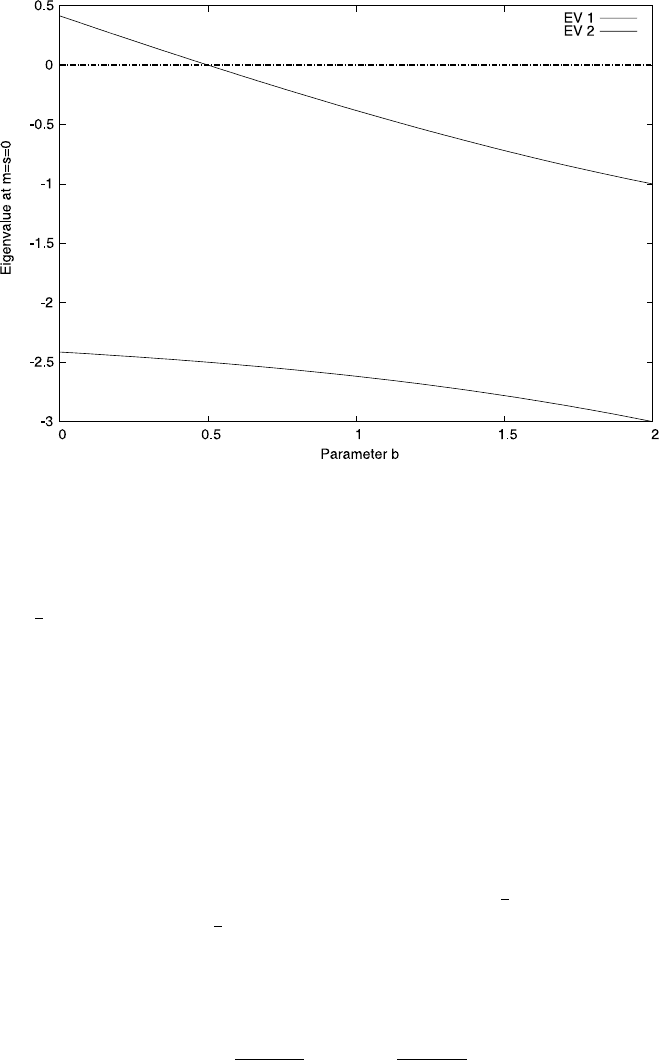
4.4 Case Study: Malaria 165

Fig. 4.12 The eigenvalues of model (4.30) at the steady states deﬁned by (4.31). We used the

parameters, a = 1, c = 1, d = 2 and we varied b.Forb<0.5 the steady states are stable, but

unstable for b>0, 5

We substitute these expressions for s

∗

and m

∗

into the Jacobian in (4.38).

J(s

∗

) =



−

ca−db

c+d

−ba(1 −

ca−db

c(a+b)

)

c(1 −

ca−db

(c+d)a

) −

ca−db

a+b

−d



We replace the symbols a, c and d with the chosen values and obtain the Jacobian.

J(s

∗

) =



−1/3 −b/31−

1−2b

1+b

2/3 +2b/3 −

1−2b

1+b

−2



Using a computational algebra system we can easily calculate and plot the eigenval-

ues for the system. Figure 4.12 shows the corresponding plot. From it is clear that

both eigenvalues are negative for b<

. This indicates stability of the non-trivial

steady states in this area. So at b =

the non-trivial and the trivial steady states not

only coincide, but also swap stability.

In summary, for this particular choice of parameters, the following picture is now

emerging:

• The system has two steady states, namely the trivial steady state (s

∗

= m

∗

= 0)

and the steady state given by (4.31).

• If we choose a =c =1 and d =2 then the non-trivial steady state is positive and

stable for b<

166 4 Differential Equations

• The trivial steady state is stable for b>

With renewed trust in the sanity of differential equation models we can now extend

our analysis to other parts of the parameter space. Without giving the details, we will

ﬁnd that both eigenvalues are negative if b<

. Similarly, the steady state deﬁned

by (4.31) coincides with the trivial steady state when b =

. This can be shown

by setting the right hand sides of (4.31) to zero and solving for b. Since the steady

state equations are strictly decreasing functions of b, this means that the non-trivial

steady state is always positive and stable for b<

and negative and unstable if

. We encourage the reader to work out the details of this argument to sharpen

her grasp of the use of these elementary, but very useful techniques, even if she has

no immediate interest in the spread of Malaria.

4.5 Chemical Reactions

Important targets of biological process modeling are chemical equations. Mathemat-

ical models can be used to analyze signal transduction cascades, gene expression,

reaction diffusion systems and many more classes of biologically relevant systems.

Given the importance of the ﬁeld, we will provide some examples of how chemical

systems can be modeled. However, again the main purpose of the case studies is to

demonstrate how to translate a qualitative understanding of a system into a formal

and quantitative differential equation model. We therefore recommend this section

to the reader even is she harbors no particular interest in chemical process modeling.

Let us start by a simple example. Assume we have two chemical species X and

Y that react to become Z witharateofk

. Let us further assume that the reaction is

reversible, that is, Z decays into its constituent parts with a rate of k

X +Y



In order to describe this set of reactions using differential equations we use the law

of mass action. This simply states that the rate of a reaction is proportional to the

concentration of the reactants. In this particular case, the rate of conversion to Z

is proportional to the concentrations of X and Y . If we denote the concentration X

by x, and similarly for Y and Z, then using the law of mass-action, we obtain a

differential equation for the system.

˙z = k

xy −k

˙y =−k

xy +k

z (4.40)

˙x =−k

xy +k

Taking a second glance at this system of equations with our (now) trained eye, we

see immediately that the equations for ˙x and ˙y are the same. Furthermore, the equa-

tion for ˙z is just the negative of that for ˙x and ˙y. This suggests that we can perhaps

describe the system with a single differential equation only.

4.5 Chemical Reactions 167

Indeed, there is an intrinsic symmetry in the system. Whenever we lose a

molecule of X, then we gain one of Z, and vice versa. Similarly, if we lose a

molecule of Y , then we gain one of Z. In other words, the sum of the concentration

of X and Z and Y and Z respectively, must be constant.

x =X

−z and y =Y

−z

Here X

and Y

correspond to the total concentration of species X and Y in the

system, and comprise both the bound and the free form of the molecule. Note that

the variables x(t) and y(t) only measure the free form. Using these relations we can

re-write the ﬁrst line in (4.40).

˙z =k

−z)(Y

−z) −k

We can solve this differential equation using the separation of variables technique:

z(t) =

θ tan(

tθ +

Cθ)

(4.41)

Here θ is a place-holder for a longer expression:



2 k

−k

−2k

−k

−2k

−k

Thesolutionin(4.41) contains an integration constant, C, that still needs to be de-

termined. We choose the concentration of Z to be vanishing at t =0, thus obtaining:

C =−2θ

−1

arctan





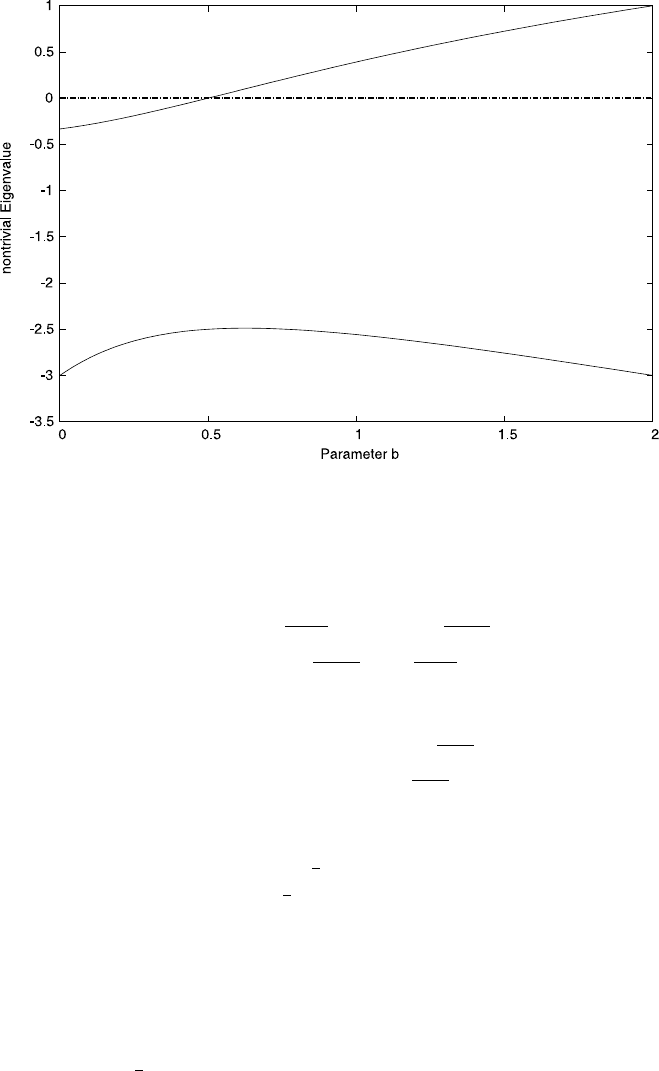
For a set of parameters we have plotted z(t) in Fig. 4.13. As expected, if we start

from z(0) = 0 then the concentration of Z increases relatively rapidly, but then

settles at a steady state. We leave a further exploration of the model as a set of

exercises.

4.11 Calculate the steady state of (4.40), both from the differential equation directly

and from the solution in (4.41).

4.12 Plot the solutions for x(t) and y(t) using the parameters in Fig. 4.13.

4.13 Without explicitly plotting the solution, what would happen if we choose a

vanishing forward reaction rate, i.e., k

=0. What would be the steady state of Z?

What would be the steady states of X and Y ?

4.14 Conﬁrm your conjectures by explicitly checking this in the model.

168 4 Differential Equations

Fig. 4.13 An example solution for z(t) in (4.41). We used the parameters, k

4.5.1 Michaelis-Menten and Hill Kinetics

Let us now modify the chemical system in (4.40) and give X a catalytic property.

X +Y



−→X +Z

In this reaction scheme we have a molecular species X (for example an enzyme)

that catalyses the reaction Y −→Z. The process proceeds in two steps. The ﬁrst step

corresponds to the formation of an intermediate compound W of the catalyst X with

the substrate Y ; after some time this compound decays into the product Z and the

original catalyst X. We could now attempt to formulate and solve the differential

equations corresponding to this system. Before doing this, however, we are going to

simplify the equations so as to be able to express the reactions in a single differential

equation. This will lead to the so-called Michaelis-Menten (MM) kinetics, which are

of fundamental importance for enzyme dynamics and beyond.

Our goal is to formulate the rate of conversion of the substrate Y into Z as a func-

tion of the amount of the enzyme X as a one-step process. A potential bottleneck

in the system is the concentration of the enzyme X. The conversion from Y to Z

has to go through intermediate binding with X; if there are only few X around, then

the availability of free X may limit the conversion rate. The MM-kinetics describes

exactly the nature of the dependence of the conversion rate on the basic system

parameters.

4.5 Chemical Reactions 169

Again using lower-case letters to denote the concentration of the respective

species denoted by upper-case letters, the full system can be described using two

differential equations.

˙w =k

xy −k

w −k

˙z = k

(4.42)

A closer look at the system reveals that the quantity w + x is conserved; that is,

each molecule of X is either free (and counted by x) or bound with a molecule of

W in which case it is counted by w. Adopting a similar notation as above, we have

x =X

−w.

˙w =k

−w)y −k

w −k

˙z = k

(4.43)

Next we will make a so-called quasi steady state approximation. This means that we

assume that the ﬁrst reaction in (4.43) happens much faster than the second. Quasi-

steady-state approximations of this sort can be very useful in systems where parts

operate on different time-scales. They are commonly encountered in the modeling

literature. In this particular case, the quasi steady state approximation is possible

because we assume that the reaction rate k

is very small compared to k

and k

If this condition is fulﬁlled, then we can replace the ﬁrst differential equation by a

normal algebraic equation in that we set its right-hand side to zero. This effectively

decouples the two differential equations. This general procedure can also be used

when the system of differential equations is very large, and is by no means limited

to systems with two equations only. The only condition for its successful applica-

tions is that the quasi-steady state assumption—that parts of the system operate on

different time-scales—is fulﬁlled.

−w)y −k

w −k

w =0 =⇒ w =X

  

The beneﬁt of taking the quasi-steady state approximation becomes immediately

clear now. We have managed to express w, the concentration of the intermediate

product that is of no interest to us, as a function of y and the total amount X

of catalyst in the system, rather than the free amount x(t). We can now substitute

this into the second line of (4.43) to obtain the equation for the Michaelis Menten

equation.

˙z =v

max

K +y

(Michaelis Menten)

Here we have deﬁned v

max

Consider the two components of the rate equation. The Michaelis-Menten func-

tion, h(y) =y/(y +K) changes from 0 to 1 as y goes from 0 to inﬁnity. It describes

170 4 Differential Equations

how increased amounts of y slowly saturate the enzyme. If we assume that the con-

centration of the catalyst, X

, is ﬁxed, then we will see initially an increasing con-

version speed as we add more substrate. However, as we add even more substrate,

the marginal increase in the conversion speed becomes smaller the higher the con-

centration of substrate. At some point, the enzymes are saturated, that is a further

increase of the substrate concentration leads to no increase in the conversion speed

(Fig. 4.14).

The MM function h(y) is actually a family of functions parameterized by the

value of K. Physically, K has a very speciﬁc meaning. The MM-function takes a

value of

when y = K; hence K deﬁnes the point where the conversion speed is

at half its maximum. If the concentration y increases much beyond K then the MM

function saturates.

The basic intuition behind the MM kinetics is easy to understand. The concen-

tration of X is a bottleneck in the system. Conversion of Y to Z takes some time.

As the concentration of y grows, there are fewer and fewer unoccupied copies of X

around and the conversion rate soon reaches capacity.

The situation is very similar to the Delicatessen counter at “Meinl am Graben”

in central Vienna. Let us suppose that there are 5 sales associates working behind

the counter and each can serve 4 customers every 10 minutes, on average. During

late afternoons, it has been observed that there are on average 10 customers arriving

every ten minutes; this means that the total volume of sales during a unit period of

time (say an hour) is about twice as high when compared to early mornings when

there are only about 5 customers every ten minutes. During the morning periods,

there is spare capacity in the system, and sales associates will be idle in between

two customers.

However, during peak times the Delicatessen counter will see 25 new customers

arriving during any period of ten minutes; they all want to buy their Milano salami

or liver paté; yet peak time sales per time unit are not 5 times the morning equivalent

because the system has reached capacity. No matter how many more customers are

arriving, the rate with which the sausages can be cut and the sandwiches prepared

will not increase. Any more customers per minute will just increase the queues, but

not increase delicatessen sales per unit intervals. The solution at this stage would

be, of course, to employ another worker to serve the customers.

In the molecular world, reactions are governed by random collisions between

molecules and there is no queuing for enzymes, yet the basic phenomenon is the

same. Just as a customer will be unlikely to ﬁnd an idle sales associate in Meinl

during peak times, so will a free molecule of Y ﬁnd that the number of collisions it

has with free X molecules become rarer as the concentration of Y increases.

The second component of the MM-kinetics is the term v

max

deﬁning the maximal

speed with which the substrate can be converted into the product. The bare-bones

MM-function h(x) always varies from zero to one. The term v

max

simply scales it

to its desired range.

Empirically, it has been found that enzyme kinetics does not obey the MM-

function, but rather a slightly modiﬁed kinetics. The so-called Hill function is a

4.5 Chemical Reactions 171

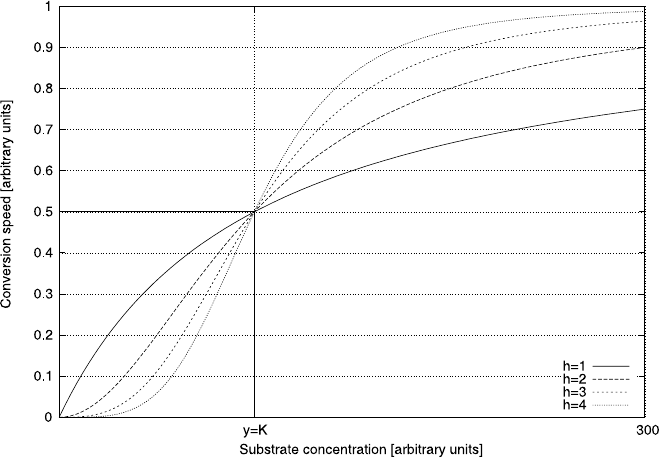
Fig. 4.14 The MM-function for K =100. It describes the speed with which the substrate is con-

verted into the product

direct extension of the MM-function (see also Sect. 2.6.2.4,p.61).

h(y) =

(Hill)

(Note that the MM-function is a Hill function with h = 1, hence we denote both

as h(x).) Just like the MM-function, Hill functions make the transition from 0 to

1 as the substrate concentration goes to inﬁnity. However, a Hill function is a sig-

moid function and makes this transition faster. As the coefﬁcient h is increased,

Hill functions increasingly resemble step functions. Just like the MM-function, Hill

functions take a value of

at y =K no matter what the value of the Hill coefﬁcient.

Figure 4.15 compares some Hill functions with the MM.

In practical modeling applications one cannot normally derive the Hill coefﬁcient

from ﬁrst principles but has to rely on empirical data. In the context of enzyme

kinetics, the Hill coefﬁcient carries some bio-chemical information about the nature

of the interactions at a molecular scale. A value of h>1 is normally interpreted

as indicating cooperativity. This means that the catalyst has more than two binding

sites for the substrate and the binding of one site increases the afﬁnity of other sites

for an additional substrate. Similarly, the inverse effect, negative cooperativity, is

indicated by a Hill coefﬁcient of h<1. It essentially means that the binding of one

site negatively affects the afﬁnity of further receptor sites. We will have more to say

172 4 Differential Equations

Fig. 4.15 Comparing the Hill functions with the MM-function for K =100. The higher the Hill

coefﬁcient the more step-like the function becomes

on this later on in this book (Sect. 6.3.3 on p. 244), when we explicitly derive a

Hill-function for the binding of transcription factors to their operator sites.

For the time being, let us now show how to use the MM/Hill function in dif-

ferential equations. In biological modeling, these functions are almost ubiquitous.

Unfortunately, normally differential equations involving MM or Hill kinetics are

difﬁcult to solve analytically and we have to be content with numerical solutions to

our differential equations.

To consider a concrete example, let us work out the model for the above system

of an enzymatic reaction.

X +Y



−→X +Z

Before we can do anything in terms of modeling, we have to specify how the sub-

strate concentration y(t) and the concentration of the catalyst x(t) change over time.

This is not clear from the above reaction scheme. For simplicity we will assume that

the latter has a ﬁxed concentration throughout, i.e., ˙x = 0 and that the former is

not replenished—the initial concentration is used up over time. At this point this

is an arbitrary decision. In practice, the differential equations for the substrate and

enzyme are normally clear from the modeling context.

Next we have to decide on the kinetic law that we wish to use to describe our

catalysed reaction. For the moment we decide just on a general Hill-kinetic while