Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

11.5 The BSSN formulation 391

−0.05

0.05

0.005

0.05

80 100 120 140

246810

200 400

600

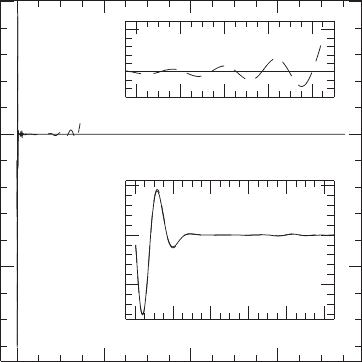
Figure 11.1 Comparison of the evolution of a linearized gravitational wave using the standard 3 + 1 or ADM

equations (dashed lines) and the BSSN equations (solid lines). Shown is the extrinsic curvature component K

as a function of time. A blow-up of the plot at early times is shown in the bottom insert, where both systems

agree very well. The evolution at later times is shown in the top insert, just before the standard 3 + 1system

crashes. For the BSSN system, which remains stable, the quantity K

is constructed from

,φ and K .[From

Baumgarte and Shapiro (1998).]

gravitational waves and the evolution of spacetimes containing black holes and neutron

stars. The BSSN system, or a variation closely related to it, is currently the form of the

Einstein’s equations most commonly used in numerical relativity. With the exception of

some that use the generalized harmonic coordinate approach of Section 11.3, most success-

ful simulations of binary black holes, binary neutron stars and binary black hole-neutron

stars, as well as stellar collapse, use a version of the BSSN system.

Constraint propagation and damping

The improved numerical stability properties of the BSSN system can be understood in terms

of the hyperbolicity criteria discussed in Section 11.1; the BSSN system can be shown to be

strongly hyperbolic, and hence well-posed, while the original 3 + 1 (ADM) formulation is

only weakly hyperbolic, and hence ill-posed.

We can also gain some heuristic insight into

its improved behavior by considering the propagation of the constraints.

Linearizing the

See, e.g., Sarbach et al. (2002); Yoneda and Shinkai (2002); Gundlach and Martin-Garcia (2006a,b), and references

therein.

Frittelli (1997).

392 Chapter 11 Recasting the evolution equations

standard 3 + 1 and BSSN equations on a ﬂat Minkowski background reveals

that modes

that violate the momentum constraint do not propagate in the standard equations. Such

zero-speed modes lead to instabilities when nonlinear source terms are included. However,

when the momentum constraint, which should be zero if the Einstein equations are satisﬁed

exactly, is added to the



evolution equation (11.43) of the BSSN system, the momentum

constraint violating modes now propagate with nonzero speed. Consequently, rather than

growing locally, as in the standard system, constraint violations can now propagate off the

numerical grid,

thereby stabilizing the simulation.

To illustrate this effect in a simple setting, let us return to Maxwell’s equations and

measure the violation of the constraint (11.6) by introducing the variable

C deﬁned

C ≡ D

− 4πρ

. (11.56)

By differentiating the continuity equation D

+ ∂

= 0 and using the evolution equa-

tion (11.5) it is easy to show that the time derivative of this constraint variable vanishes

identically,

∂

C = ∂

− 4πρ

) = D

∂

− 4π∂

=−D

+ D

− 4π(D

+ ∂

) = 0. (11.57)

This result indicates that any violation of the constraint (i.e.,

C = 0) will persist and not

propagate away.

The situation is different in the BSSN-like reformulation of Maxwell’s equations of

Section 11.2.3. In fact, we can use this example to show the effect of adding the constraint

(11.6) in the evolution equation (11.17). Instead of using the constraint to completely

replace the divergence D

aswedidinderivingthe-evolution equation (11.17),

consider adding the constraint violation parameter

C times some constant a

(which we

are always allowed to do, since constraint violations are supposed to vanish),

∂

 = ∂

= D

∂

=−D

− D

 + a

= (a

− 1)D

− D

 − 4π a

. (11.58)

With a

= 1werecoverequation(11.17). We can now reconsider the propagation of the

constraint violations, i.e., the time evolution of the parameter

C.Inderivingequation(11.57)

we used the evolution equation (11.5), but this evolution equation is no longer part of the

new BSSN-like evolution system consisting of equations (11.4), (11.17) and (11.18). For

this system, we can show that the constraint violation parameter now satisﬁes a wave

equation.

Alcubierre et al. (2000).

Provided that appropriate boundary conditions are imposed.

See Knapp et al. (2002), who demonstrate this effect in a numerical example.

11.5 The BSSN formulation 393

Exercise 11.4 Show that in the system (11.4), (11.17)and(11.18) constraint vio-

lations measured by the parameter

C deﬁned in equation (11.56) satisfy the wave

equation

(−∂

+ a

) C = 0. (11.59)

According to equation (11.59), constraint violations measured by C now propagate like

waves with a characteristic speed a.Fora = 0, the constraints again do not propagate, but

with a = 1 they propagate with the speed of light. We thus see that adding the constraint

in equation (11.17) was crucial in achieving this property, in direct analogy to the results

found for the linearized Einstein equations.

If the condition

C = ∂

C = 0 holds initially, then the two systems are equivalent ana-

lytically, since both will guarantee that

C = 0 in the domain of dependence of the initial

spatial hypersurface. However, the two systems behave very differently numerically, since

any numerical (e.g., roundoff) error will lead to a constraint violation |

C| > 0, which will

then evolve differently in the two systems.

The addition of the constraints to the evolution equations, which comes under the general

category of constraint damping or constraint sweeping, is by no means unique to the BSSN

system. We have already discussed in Section 11.1 that adding constraints to the evolution

equations affects the principal part of the system, and hence its well-posedness. This

technique has been applied in the context of MHD, as we mentioned in Chapter 5.2.4.Itwas

pointed out early on

that constraint violations can be controlled by adding additional terms

to the standard 3 + 1 evolution equations. The importance of the propagation of constraints

in unconstrained evolution calculations was demonstrated and shown to be linked to the

addition of the Hamiltonian constraint to the evolution equations.

Several investigators

have also experimented with adding the momentum constraints to the standard equations

and have found stabilizing effects.

We have already mentioned that in the presence of

black holes, the generalized harmonic approach summarized in Section 11.3 requires the

addition of constraints. It also turns out that in some situations the stability properties of

the basic BSSN system itself can be enhanced further by explicitly adding Hamiltonian

and/or momentum constraints.

We will describe some of these enhancements when we

discuss a few speciﬁc applications that employ the BSSN formalism in later chapters.

Detweiler (1987).

Frittelli (1997); see also Kelly et al. (2001).

See, e.g., Yoneda and Shinkai (2001).

See Yoneda and Shinkai (2002); Yo et al. (2002); Duez et al. (2004); Marronetti (2005, 2006).

See, e.g., Chapter 14.2.3.

Binary black hole initial data

In this chapter we wish to construct initial data for quasiequilibrium binary black holes. That

is, we seek solutions corresponding to two black holes in stable, nearly circular orbit about

each other. In contrast to Newtonian theory, a stellar binary in general relativity can never

be in strict equilibrium, with the companions moving in exactly circular orbits at constant

separation for all time. Instead, gravitational radiation emission inevitably leads to loss of

orbital energy and angular momentum, causing the orbit to decay. The resulting trajectory

then traces out an inspiral rather than a perfect circle. For sufﬁciently large separations,

the binary motion is nearly Newtonian, hence the orbit is nearly circular, decaying very

little during one orbital period. If isolated from outside perturbations (e.g., gravitational

encounters with other stars), it is expected that astrophysical binaries composed of compact

stars (i.e., compact binaries) will ultimately evolve to a quasiequilibrium state following

their formation at large separation.

The reason is that gravitational radiation loss drives

orbital circularization as well as decay, as we will discuss in the next section. Only when

the orbits become very close and highly relativistic, just prior to radial plunge and binary

merger, do the deviations from circular motion become large.

The construction of quasiequilibrium binary initial data poses a number of conceptual

challenges. Getting started, however, is fairly straightforward. To ﬁnd solutions we shall

follow the approaches outlined in Chapter 3. Speciﬁcally, we need to solve the constraint

equations (2.132) and (2.133), which can be cast into a convenient form with the help of

the conformal transformation (3.5)ofthespatialmetricγ

= ψ

¯γ

. (12.1)

Recall that ψ is the conformal factor and ¯γ

the conformally related metric. Recall also that

we can separate the trace of the extrinsic curvature from its traceless part and conformally

rescale the latter according to equation (3.35), so that

= ψ

−2

K. (12.2)

Exceptions include extreme-mass-ratio binaries consisting of stellar-mass companions (which may be compact stars)

orbiting supermassive black holes in dense stellar systems. The orbits of the companions, which evolve via gravitational

encounters (scattering) with other stars as well as by gravitational radiation reaction forces, may be highly eccentric.

See Chapter 9.2.2 for discussion and references.

394

12.1 Binary inspiral: overview 395

In terms of these quantities the Hamiltonian constraint then takes the form (3.37),

ψ − ψ

R −

+ ψ

−7

= 0, (12.3)

while the momentum constraint reduces to equation (3.38),

−

¯γ

K = 0. (12.4)

Here we have specialized to the binary black hole problem and assumed that all matter

sources vanish.

In Chapter 3.1 we saw that under the assumption of time-symmetry (where K

0) solutions containing multiple black holes can be constructed remarkably easily (see

equation 3.23). Unfortunately, binary black holes in circular orbit are not time-symmetric,

so that these simple solutions are not useful for purposes of obtaining quasiequilibrium

solutions. In Chapter 3 we discussed two separate decompositions of the traceless part

of the extrinsic curvature

, namely the transverse-traceless decomposition (CTT) in

Chapter 3.2 and the conformal thin-sandwich decomposition (CTS) in Chapter 3.3.We

will follow a very similar approach again in this chapter, adopting CTT in Section 12.2

and CTS in Section 12.3. Before constructing these binary black hole initial data, we ﬁrst

shall review some of the physical characteristics of compact binary inspiral, which will

motivate some of the choices that we will make in later sections.

12.1 Binary inspiral: overview

The evolution of compact binaries – binary black holes, neutron stars, or black hole-

neutron stars – proceeds in several distinct phases. By far the longest epoch is the initial

inspiral phase, followed by the plunge and merger phase when the two objects coalesce,

and ﬁnally the ringdown phase during which the merger remnant settles down to stationary

equilibrium. These different phases are illustrated schematically in Figure 12.1.

As long as the binary is nearly Newtonian, with the orbital separation much larger than

the total mass M, we may model the emitted gravitational waves as small perturbations

propagating on an otherwise ﬂat background spacetime. As reviewed in Chapters 1.1

and 9.1 the losses of orbital energy and angular momentum in the weak-ﬁeld, slow-velocity

regime appropriate to Newtonian binaries are then given to lowest order by the quadrupole

expressions,

≡−



...

 (12.5)

and

=−



ijk



...

. (12.6)

Remember that all barred quantities are associated with the conformally-related metric.

396 Chapter 12 Binary black hole initial data

h(t )

quasi-circular

inspiral

plunge

merger

ringdown

post-Newtonian

techniques

numerical

relativity

perturbation

methods

Figure 12.1 The different phases of compact binary inspiral and coalescence. The gravitational wave amplitude

h(t) is sketched schematically and the analysis technique is identiﬁed for each phase.

Here I

is the reduced quadrupole moment,

≡





−



x =





−



, (12.7)

the bracket denotes an average over several orbital periods, and the triple dot denotes

the third time derivative. For a binary at large separation we may treat the stars as point

masses and insert their stellar masses m

and Newtonian trajectories x

(t) into equa-

tion (12.7) to evaluate equations (12.5) and (12.6). For a binary orbit with eccentricity e the

emission of gravitational radiation always leads to a decrease in the eccentricity,

e < 0.

Put differently, gravitational radiation circularizes elliptical orbits. This result implies

that during the late stages of compact binary inspiral, we may approximate the orbit as

circular.

Exercise 12.1 Consider a Newtonian binary consisting of two point masses m

and

at a binary separation r. Write the binary’s Hamiltonian H (r,φ,P

, P

), which

is equal to its conserved energy E,as

E = H =

µr

−

µM

, (12.8)

where M = m

+ m

is the total mass and µ = m

/M is the reduced mass. Deﬁne



orb

≡

φ to be the orbital angular velocity, and J ≡ P

to be the orbital angular

momentum.

Peters (1964); see also Lightman et al. (1975), Problem 18.7.

See also exercise 12.2, which shows that once they become circular, the orbits remain circular as they shrink in radius.

12.1 Binary inspiral: overview 397

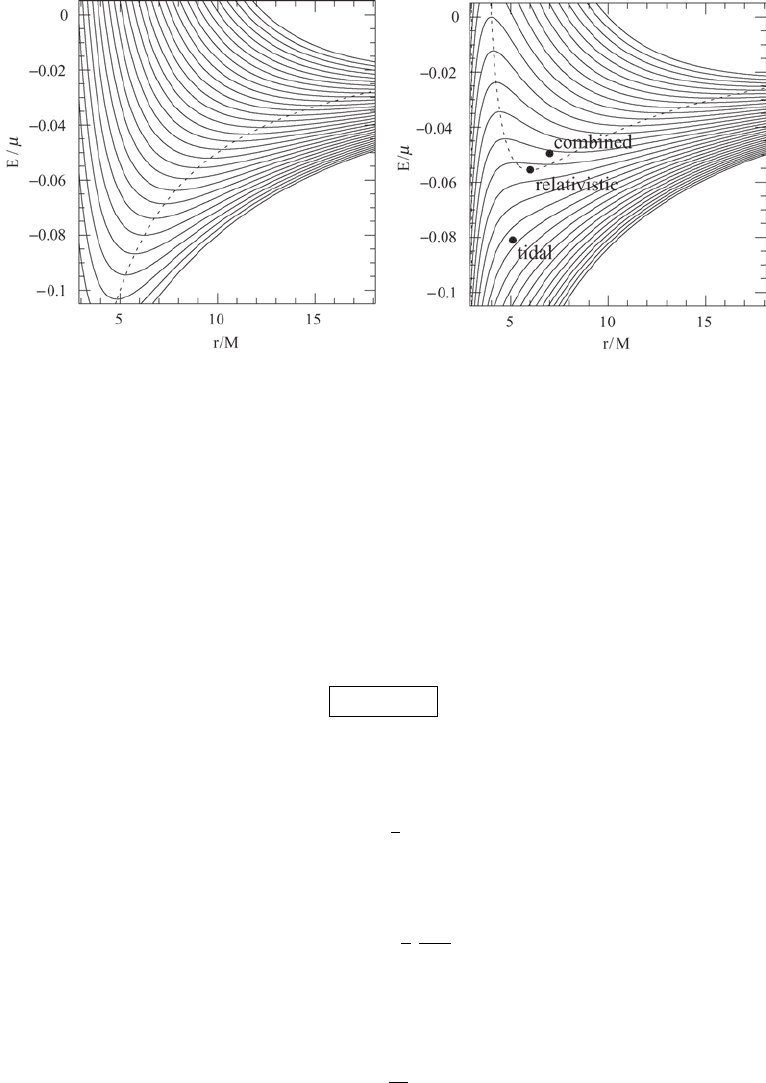
Figure 12.2 The energy E as a function of separation for a point-mass Newtonian binary (left panel), and a toy

model problem that incorporates relativistic effects (right panel). The solid lines are contours of constant angular

momentum J , with the values of J increasing from the bottom to the top. Extrema of these contours correspond

to circular orbits (equation 12.9). The dashed line connects the circular orbits and represents the equilibrium

energy E

. A turning point in this equilibrium energy represents the ISCO (equation 12.13)andismarkedby

dots for relativistic, tidal and combined relativistic and tidal effects. [From Baumgarte (2001).]

(a) Use Hamilton’s equations to show the following: P

= µ

r, J = µr



orb

,andJ

is conserved.

(b) Apply Hamilton’s equations to show that a circular orbit with P

= 0

satisﬁes

∂ E/∂r = 0. (12.9)

the kinetic energy T and potential energy W ,

T =−

W, (12.10)

which implies that the binary’s equilibrium energy is

(r) =−

Mµ

. (12.11)

(d) Use the virial theorem to evaluate 

orb

for circular equilibrium, obtaining Kepler’s

third law,



orb





1/2

. (12.12)

398 Chapter 12 Binary black hole initial data

The condition (12.9) shows that we can identify a circular orbit by ﬁnding an extremum of

the energy at constant angular momentum, which we illustrate in Figure 12.2. A minimum

of the energy corresponds to a stable circular orbit, while a maximum corresponds to an

unstable orbit. The left panel in the ﬁgure plots the Newtonian energy (12.8), for which

circular orbits can be found for arbitrarily small binary separations. The transition between

stable and unstable circular orbits occurs at a turning point in the equilibrium energy curve,

i.e., when

∂ E

/∂r = 0. (12.13)

Equation (12.13)istheturning-point criterion for indentifying marginal stability in an

equilibrium conﬁguration, including a circular binary orbit.

For Newtonian point-mass

binaries, the extrema of the energy are all minima, as seen in the ﬁgure; equivalently, there

are no turning points in the equilibrium energy curve, as indicated by equation (12.11)

and by the shape of the equilibrium energy curve plotted in the ﬁgure. Hence all of these

circular orbits are stable. Condition (12.9), which identiﬁes circular orbits, is equivalent

to imposing the virial theorem (12.10) at every instant of time (and not simply as an orbit

average, which applies for eccentric orbits also). These same general criteria for ﬁnding

quasiequilibrium binaries obeying the virial theorem and identifying the onset of orbital

instability also apply to relativistic systems (see, e.g., exercise 12.4), and they will be used

in Sections 12.2.3 and 12.3.3.

Exercise 12.2 Return to exercise (12.1) and show that changes in the equilibrium

energy E

(r) and the angular momentum J

(r) of Newtonian point-mass binaries

that reside along sequences of circular equilibrium are related according to

= 

orb

. (12.14)

Combined with the results of Exercise 9.3, which shows that the energy and angu-

lar momentum emitted by gravitational radiation satisfy the same relation, equa-

tion (12.14) implies that gravitational wave-driven binary inspiral will leave circular

orbits circular.

As we have mentioned, an exactly circular orbit can only exist in Newtonian gravity,

since in general relativity gravitational radiation makes the orbit shrink.

We can estimate

the orbital decay rate dr/dt and the time dependence of the radial separation r(t) from

equation (12.5), as shown in exercise 12.3.

We apply the same turning-point criterion to identify the onset of radial instability in equilibrium stars in Chapters 1.3

and 14.1.2.

Unless, of course, the loss of energy and angular momentum by gravitational radiation emission is exactly cancelled

by some ad hoc incoming gravitational radiation. In fact, several authors have suggested approaches for modeling

equilibrium relativistic binaries by invoking such a “standing-wave” approximation to maintain exactly circular orbits

(see, e.g., Detweiler 1989; Andrade et al. 2004).

12.1 Binary inspiral: overview 399

Exercise 12.3 (a) Revisit the Newtonian binary of exercise 12.1 and use the results

of exercise 9.3 to show that

(12.15)

for a circular orbit.

(b) Combine equation (12.15) with the binary’s equilibrium energy E

to ﬁnd

/dt

/dr

=−

/dr

=−

. (12.16)

Now integrate equation (12.16) to ﬁnd the binary separation r as a function of time,

r(t) = 4



µM

(T − t)



1/4

, (12.17)

where T is the time of the coalescence when r = 0.

wave quadrupole frequency as a function of time,

(t) =



orb

8π



µM

2/3

(T − t)



3/8

. (12.18)

(d) Gravitational wave interferometers are sensitive to the number of wave cycles

cyc

observed in a given wave frequency interval df

. Show that for the Newto-

nian binary, one obtains a “chirp signal”

cyc

d ln f

≡

/dt

96π

(πM f

)

5/3

, (12.19)

where

M ≡ µ

3/5

2/5

is called the “chirp mass”. Note that post-Newtonian correc-

tions to equation (12.19) can be expressed as a series expansion in the parameter

M f

 1.

In exercise 12.3 we adopted circular orbits to estimate the deviation from circular motion.

This procedure is justiﬁed as long as the deviation from circular motion is small. To assess

the deviation from circularity, we ﬁrst deﬁne the orbital decay time scale τ

due to

gravitational wave emission according to



dr/dt



. (12.20)

Substituting equation (12.16)weﬁnd

. (12.21)

We can now compare this orbital decay time scale with the orbital period,

P =

2π



orb

= 2π





−1/2

, (12.22)

400 Chapter 12 Binary black hole initial data

by forming the dimensionless ratio

128π

5/2

3/2

. (12.23)

For a binary of mass ratio q we can express equation (12.23)as

128π

(q + 1)





5/2

. (12.24)

This ratio increases steeply with r and is greater than unity, thereby justifying the assump-

tion of circular orbits, provided

crit

≡



128π



2/5

(1 + q)

4/5

≤ 5.78. (12.25)

The critical separation r

crit

takes its maximum value of 5.78M for equal-mass binaries

with q = 1. This value suggests that we may indeed approximate the binary orbit during

the inspiral phase as quasicircular up to very small binary separations, on the order of a

few Schwarzschild radii.

At these small binary separations deviations from the simple Newtonian point-mass

potential in equation (12.8) affect the binary’s evolution, both quantitatively and quali-

tatively. Deviations stem from relativistic corrections to the Newtonian interaction and

from ﬁnite-size effects that lead to tidal interaction between the binary companions. Post-

Newtonian techniques can handle the relativistic perturbations to the point-mass inspiral,

furnishing the corrections as a power series in the parameter  ≡ v

∼ GM/r (see

Appendix E). Numerical simulations are required to handle tidal interactions, as well as

the late inspiral, plunge and merger phases when relativistic and, in the case of neutron

stars, hydrodynamic effects become increasingly strong.

Consider how these corrections to the Newtonian point-mass potential lead to qualita-

tively new features in the binary orbit. We can mimic the effect of the relativistic correction

by borrowing a relativistic interaction potential

rel

=−

(12.26)

from the effective potential for test particles in a Schwarzschild spacetime (see exer-

cise 12.4). Adding this term to the Newtonian energy (12.8) and evaluating the circular

equilibrium criterion (12.9) shows that circular orbits now have the equilibrium energy

=−

Mµ

r − 4M

r − 3M

. (12.27)

This relativistic “toy model” is also illustrated in the right panel of Figure 12.2. Without

the new term, the energy curves at constant angular momentum are dominated by the

positive kinetic energy term J

/(2µr

) at small binary separations r . With the addition

of the relativistic correction, however, these curves are dominated by the new negative

term (12.26) for small r. For sufﬁciently large J this correction adds a new maximum to