Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

13.2 Binary black hole inspiral and coalescence 441

−1400 −1200 −1000 −800 −600 −400 −200 0

−0.2

−0.15

−0.1

−0.05

0.05

0.1

0.15

0.2

0.25

time (M)

rh (M)

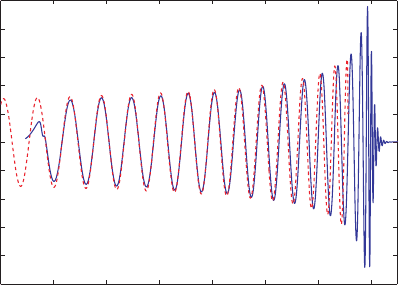
Figure 13.7 Comparison of the gravitational waveform h(t) from an equal-mass, nonspinning black hole binary

as obtained in the numerical simulations of Baker et al. (2007a) (solid line) with the corresponding

post-Newtonian result to order 2.5PN in the amplitude and order 3.5PN in the phasing (dashed line; see Blanchet

2006). Here r is the distance to the source. The gravitational wave strain h is based on the dominant l = 2, m = 2

spin-weighted spherical harmonics of the radiation and represents an observation made in the system’s equatorial

plane, where only the h

polarization contributes to the strain. [From Baker et al. (2007a).]

Figure 13.6 demonstrates mass-energy conservation in the calculations of Baker et al.

(2006a). This calculation used AMR, with a grid resolution of x = M/32 on the ﬁnest

grid, and with the outer boundary at 128M. The comparison is performed for gravitational

wave extraction at both 40M and 50M. Except for some ﬂuctuations at early times, caused

by a transient pulse in the gauge evolution that affects the measurement of the ADM

mass, the agreement is remarkably good, and provides one measure of the accuracy of the

simulation.

In a follow-up study, Baker et al. (2007a) compared their gravitational waveforms

with those obtained from post-Newtonian approximations.

For such a comparison it is

important to start the inspiral from a large binary separation, where one would expect the

two approaches to agree well. Baker et al. (2007a) therefore use as initial data a binary with

an orbital angular frequency of approximately M = 0.0255, which may be compared

with the values at the ISCO listed in Table 12.2. This binary completes about seven

orbits, and hence about 14 gravitational wave cycles, before coalescence. The agreement

with post-Newtonian predictions well into the merger phase is remarkable. Figure 13.7

compares the gravitational waveform generated by the numerical simulations with the the

post-Newtonian prediction to order 2.5PN in the amplitude and to order 3.5PN in the phase.

The numerical simulation uses fourth-order ﬁnite differencing, AMR, and a resolution of

See Appendix E as well as Blanchet (2006).

442 Chapter 13 Binary black hole evolution

approximately M/32 on the ﬁnest grid. While the agreement is not perfect, it is consistent

with the internal error estimates in either one of the two approaches.

Given the different algorithms and implementations used in the simulation of binary

black holes, it is of interest to compare how well predictions from these different codes

agree. This has been addressed by Baker et al. (2007b), who provide a comparison of the

results obtained with the codes of Pretorius (2005a), Campanelli et al. (2006)andBaker

et al. (2006a). If the only differences between these simulations originate in the adopted

formulation of Einstein’s equations, gauge conditions and speciﬁcs of the numerical imple-

mentation, then clearly all of them should yield the same results for physical invariants

in the limit of inﬁnite resolution. However, the simulations differ in other aspects, too.

One difference lies in the initial data. For the calculations presented in Buonanno et al.

(2007), Pretorius adopts the corotational, conformal thin-sandwich binary black hole data

of Cook and Pfeiffer (2004). The other two groups, on the other hand, adopt nonspinning

puncture initial data. Even though the simulations start with quasiequilibrium initial data

describing a binary at quite similar proper separations and angular velocities, they carry

different total angular momenta.

Moreover, the different groups use different algorithms

for the extraction of gravitational waves (see Chapter 9.4). Despite these differences, it is

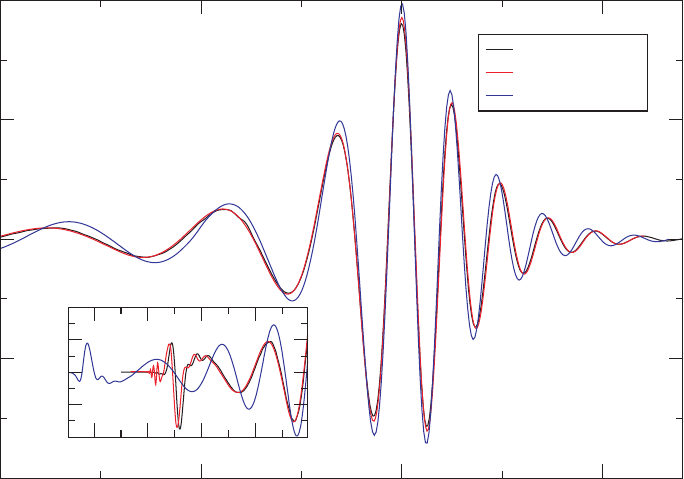
remarkable how well the predictions for the asymptotic gravitational wave signals agree, as

showninFigure13.8. The agreement is particularly convincing for the waveforms emitted

during the merger phase. At earlier times, shown in the inset, especially when the signal is

dominated by noise associated with the initial data, the agreement is worse, as one would

expect.

Figures 13.7 and 13.8 also demonstrate how “simple”, in some sense, the gravitational

wave signal from the merger of a binary black hole system appears. One can easily

identify the familiar “chirp” signal, emitted during the late inspiral phase, during which

both the wave amplitude and frequency increase. The signal terminates, as expected, with

quasinormal ringing, as the merger remnant settles down to stationary equilibrium. The

transition from the chirp to the ringdown part of the signal is rather smooth, and not at

all abrupt. This feature is related to the relatively smooth transition of the binary orbit

from inspiral to merger, as described in Chapter 12. While we have deﬁned and located

the ISCO as the last stable circular orbit for the quasiequilibrium models considered in

Chapter 12, the ISCO does not mark a very sudden transition, but rather a gradual change

from inspiral to plunge. This can be seen in Figure 13.4, which displays no sharp plunge

prior to merger.

In fact, the inspiral is approximated remarkably well by the Newtonian quadrupole

expressions of Exercise 12.3 until late times.

A dynamical instability in the binary orbit

A similar analysis, based on the numerical simulations of Pretorius (2005a), has been presented in Buonanno et al.

(2007).

Even for identical angular momenta, the quasiequilibrium data constructed from the conformal thin-sandwich approach

and the puncture data may not represent slices of identical spacetimes; see the discussion in Chapter 12.

See Buonanno et al. (2007) for a detailed analysis.

13.2 Binary black hole inspiral and coalescence 443

−100

−50

t/M

−0.04

−0.02

0.02

0.04

r ψ

GSFC (R1)

UTB (s00)

Pretorius (d16)

−250

−200

−150

−100

−0.004

−0.002

0.002

0.004

Figure 13.8 Comparison of the gravitational waveforms Re(ψ

) obtained by three independent research groups:

Pretorius (Pretorius 2005a; Buonanno et al. 2007), Goddard Space Flight Center (GSFC, e.g., Baker et al.

(2006a) and University of Texas at Brownsville (UTB, e.g., Campanelli et al. 2006). [From Baker et al. (2007b).]

at the ISCO should be reﬂected in a departure of the waveform from this expression.

However, a common horizon forms sufﬁciently early to absorb much of the radiation

generated during such an epoch and mask any such departure.

Simulations that can track binary black hole inspiral from large separation allow us to

estimate the total energy emitted in gravitational radiation during the entire coalescence

event. Baker et al. (2007b) ﬁnd that approximately 3.5% of the total initial mass-energy

M is radiated away during the late inspiral and merger, starting from a proper horizon

separation of about 10M; other investigations are in reasonable agreement. The amount

of energy radiated during the early inspiral from inﬁnite separation to the separation of

10M can be estimated from the binding energy of the initial data at 10M. Using the

values reported in Caudill et al. (2006)andBuonanno et al. (2007), the radiated energy

is about 1.2% of M.

The total amount of energy radiated during inspiral from inﬁnite

separation is therefore between about 4.5 and 5% of the total initial mass-energy. This value

is signiﬁcantly less than the maximum possible value of 29% allowed by the area theorem

See Tables 12.1 and 12.2, where we list the binding energies at the ISCO, i.e., at slightly smaller binary separation.

444 Chapter 13 Binary black hole evolution

0 1000 2000 3000

−0.002

−0.001

0.001

0.002

Re(r M Ψ

) l=2, m=2

3800 3900 4000

−0.06

−0.03

0.03

0.06

− r

)/M(t

− r

)/M

− r

)/M

0 1000 2000 3000

0.0001

0.0003

0.001

0.003

Re(r M Ψ

) l=2, m=2

| r M Ψ

| l=2, m=2

3800 3900 4000

−5

−4

−3

−2

−1

− r

)/M

Figure 13.9 The gravitational waveform, extrapolated to spatial inﬁnity, for an equal-mass, nonspinning, black

hole binary. The top panel shows the real part of the dominant l = 2, m = 2 mode of ψ

on the linear scale, the

bottom panel on a logarithmic scale. The panels on the right show an enlargement of the data for the merger and

ringdown. [From Scheel et al. (2009).]

(see exercise 7.2), but considerably more than the energy radiated during a head-collision

fromrestatinﬁnity( 1%; see Chapter 10.2.)

Building on these initial successes, many other investigators followed up with their own

simulations of the inspiral and merger of equal-mass binary black holes. As an example

we show results from a highly reﬁned simulation, based on a carefully groomed, pseudo-

spectral implementation of a ﬁrst-order version of the generalized harmonic formalism, in

Figure 13.9.

In Appendix I we present results in greater detail for two simulations of the inspiral and

merger of nonspinning binary black holes. One simulation describes an equal-mass binary

and the other describes a binary with a mass ratio of 3:1 (see the following section). These

particular simulations employ a ﬁnite difference implementation of the moving puncture

method within the BSSN formalism and employ puncture initial data. In the Appendix

we tabulate speciﬁc information about the adopted AMR grid set-up, the ﬁnite difference

implementation, the initial data, and the diagnostics, as well as the emitted gravitational

radiation and the black hole recoil. We also plot the orbital trajectories of the black

holes and the emitted gravitational waveforms. The purpose of this Appendix is twofold:

First, from a practical computational perspective, these two simulations provide handy

See Scheel et al. (2009), as well as Lindblom et al. (2006), for a ﬁrst-order version of the generalized harmonic

formalism.

13.2 Binary black hole inspiral and coalescence 445

test-bed calculations for researchers seeking to perform similar simulations with their

own algorithms and vacuum codes. Second, from a pedagogical perspective, the summary

provided in the Appendix pinpoints where in the course of performing and evaluating a

binary black hole simulation one is required to implement many of the basic concepts and

tools that have been developed in this book. References to the places in the book where

these concepts and tools are introduced are provided throughout Appendix I.

13.2.2 Asymmetric binaries, spin and black hole recoil

In the last section we focused on equal-mass, nonspinning binaries. While this is a very

natural case to study ﬁrst, it clearly is not a generic scenario: binary black holes in nature

are likely to have unequal masses and nonzero spins. It therefore is of great interest to

understand how the ﬁndings of the previous section change for mass ratios different from

unity and how they are affected by black hole spin.

Allowing for unequal masses and black hole spin will certainly alter the gravitational

signal emitted during the inspiral and merger. It is therefore crucial to understand these

effects for the detection of gravitational waves from binaries. In fact, the accurate extraction

of binary parameters from an observed gravitational wave signal requires a large catalog

of templates of theoretical waveforms compiled for binaries with different mass ratios and

spin parameters.

However, the detection and interpretation of gravitational wave signals is not the only

astrophysical motivation for the study of asymmetric binaries. As it turns out, one important

consequence – black hole recoil – is suppressed in the symmetric binary scenarios of

Section 13.2.1, but plays an important role in several different astrophysical contexts, as

we will sketch below.

Black hole recoil can be understood qualitatively as follows. Gravitational radiation gen-

erally carries both energy and momentum. In symmetric binaries, the total linear momen-

tum radiated by the binary must be zero: the contributions to the radiated linear momentum

from the two black holes cancel. This cancelation does not occur in an asymmetric binary,

which therefore radiates a nonzero net linear momentum. Given this linear momentum loss,

the center of mass of the system acquires a linear momentum in the opposite direction.

In a frame in which the binary’s center of mass was originally at rest prior to merger, the

remnant will thus end up with a nonzero “kick” velocity.

Just how large this recoil or kick velocity V

kick

is has important astrophysical and

cosmological implications. For example, supermassive black holes with masses in the

range 10



− 10



are believed to reside at the centers of many, if not most, bulge

galaxies, including the Milky Way. One plausible scenario for their formation is through a

combination of mergers with other black holes and gas accretion. The mass and age of the

initial “seed” black hole is unknown, but it could be in the range 60−600M



if it is the

collapsed remnant of a ﬁrst-generation Population III star,

or much higher than 10



Madau and Rees (2001).

446 Chapter 13 Binary black hole evolution

if it is the remant of a collapsed supermassive star.

Binary black holes can form during

the merger of their host galaxies. This process is believed to be take place in the context of

the cold dark matter (CDM) model of structure formation in the early Universe, where

dark matter halos merge hierachically and black holes are assumed to settle, merge and

accrete in their gaseous centers.

Clearly, for the remnant of such mergers to remain within any host, the kick speed V

kick

has to be less than the escape velocity of that host. In giant elliptical galaxies and spiral

galaxies, the central escape velocities V

esc

are roughly between 500 km/s and 2000 km/s.

If kick speeds routinely exceeded these escape speeds, this would clearly call into question

whether supermassive black holes can form via hierarchical merger,

and might favor

instead growth via pure accretion, or some other mechanism. On the other hand, even a

modest kick speed V

kick

would be sufﬁcient to explain the apparent absence of massive

black holes in dwarf galaxies and globular clusters, for which the central escape speed is

signiﬁcantly smaller than for giant galaxies.

A typical kick speed just below the escape speed should result in a ﬁnite probability of

ﬁnding remnant supermassive black holes displaced from the center of their host galaxies.

Eventually, dynamical friction (gravitational scattering off other stars) will cause the orbit

of the black hole to decay back to the galaxy center, as it transfers kinetic energy to the

other stars in the galactic nucleus.

The ejection of merger remnants from globular clusters reduces the likelihood of further

mergers and thus decreases the probability of observing binary black hole mergers in such

clusters. For the same reason, black hole merger remnants have difﬁculty remaining in

high redshift halos with relatively shallow potential wells.

Another important consequence of black hole mergers is its effect on the spin evolution

of a supermassive black hole. The growth rate of a black hole by gas accretion is a function

of its efﬁciency of conversion of accreted rest-mass into electromagnetic radiation, and

this efﬁciency depends sensitively on the spin parameter a/M of the black hole. Black

holes with smaller spin parameters have lower efﬁciency and thus grow more quickly for

a given luminosity. It is thus a crucial question whether or not the combination of mergers

and gas accretion at the Eddington limiting luminosity

is sufﬁciently rapid to build a

supermassive black hole to power QSO SDSS 1148 + 5251, the quasar with the highest

known redshift (z = 6.4) at the time of the writing of this book. This quasar is believed to

host a 10



black hole, which therefore implies that a seed black hole must be able to

grow to this size within 0.9 Gyr after the Big Bang in the standard CDM cosmology. The

See Rees (1984)andShapiro (2004b) for discussions of supermassive star collapse and alternative scenarios for

forming supermassive black hole seeds. See Chapter 14.2 for simulations of massive star collapse to black holes.

See, e.g., Figure 2 of Merritt et al. (2004) for the central escape speeds of various types of galaxies and star clusters.

We note that the kick speed is independent of the total mass of the binary, a result that is consistent with the fact that,

when expressed in gravitational units, speed is dimensionless.

See Volonteri (2007) and references therein for calculations of the effect of recoil on the formation of supermassive

black holes.

The Eddington limit L

Edd

is the critical luminosity at which the outward force of radiation pressure equals the inward

pull of gravity in an accreting plasma. See, e.g., Shapiro and Teukolsky (1983), Section 13.7 for a derivation.

13.2 Binary black hole inspiral and coalescence 447

existence of this black hole may constrain the spin evolution of its accreting progenitors

and the viability of the merger-accretion scenario for supermassive black hole growth.

We note that each time binary black holes of comparable mass merge (a “major merger”),

the remnant acquires an appreciable spin, arising largely from the orbital angular momen-

tum of the binary near the ISCO. For example, the merger of two equal-mass, nonspinning

black holes results in a remnant with spin parameter a/M ≈ 0.7(seeTableI.4). By con-

trast, the merger of a massive black hole with multiple small-mass companions (“minor

mergers”) that inspiral in isotropically-oriented orbits will spin down the massive black

hole as it grows.

Gaseous disk accretion will drive up the spin of the black hole; spin

equilibrium will be achieved for a value of a/M that depends on precise details of the

accretion process. For example, ignoring radiation loss, accretion from a standard relativis-

tic “thin disk” will drive the spin up to its maximal value, a/M = 1,

while accounting for

photon emission shifts the equilibrium value back down to a/M = 0.998.

Simulations

of relativistic MHD accretion onto Kerr black holes, however, suggest that the disk may

not be so thin and the equilibrium spin value may be signiﬁcantly lower, a/m ∼ 0.9.

The spin of a supermassive black hole at any one time may thus be determined by the

mechanism that has dominated its most recent growth.

Finally, as we will see below, the merger of spinning black holes of comparable mass

may cause the spin axis of the remnant to ﬂip. It has been speculated that this phenomenon

could explain the observation of X-shaped radio jets, in which the orientation of the emitted

jets seems to have changed abruptly in the past.

Unequal masses

Historically, black hole recoil was ﬁrst considered for unequal-mass binaries with non-

spinning companions. In such a binary the less massive star or black hole resides at a

larger separation from the center of mass than the more massive companion, and hence

orbits with a larger orbital speed. The two objects therefore emit gravitational radiation

at different rates, and, in a crude analogy to electromagnetism, the radiation from the

faster object is more highly “beamed” in the forward direction than the radiation from the

slower object. As a consequence the linear momentum emitted from the two companions

no longer cancel, hence the center of mass acquires some linear momentum in the process.

In the absence of spin, the situation is symmetric across the orbital plane, which implies

that the radiation reaction force must lie in this plane. Over the course of one orbit the

direction of the force also completes a full circle – similar to a spinning lawn sprinkler that

See Shapiro (2005)andVolonteri and Rees (2006) for discussion and references.

a/M ∼ M

−7/3

; Hughes and Blandford (2003); Gammie et al. (2004). Spindown occurs because the orbital angular

momenta of counter-rotating companions at their ISCOs are larger in magnitude than those of corotating companions.

Bardeen (1970).

Thorne (1974).

De Villiers et al. (2003); Gammie et al. (2004).

See Berti and Volonteri (2008) and references therein for studies of cosmological black hole spin evolution by mergers

and accretion, with observational implications.

448 Chapter 13 Binary black hole evolution

ejects water in a rotating beam. If the orbit were strictly circular, the motion of the center of

mass would therefore also describe a circle, making the net effect vanish. Instead, however,

the binary orbit inspirals slowly, so that the binary emits slightly more linear momentum

at the end of one orbit than at the beginning. As a consequence, the center of motion does

not follow a perfect circle, but instead describes an outward spiral – which can be pictured

by imagining a spinning lawn sprinkler that emits water at an increasing rate. The process

ends when the binary merges and ceases to emit linear momentum. At that point the center

of mass will follow a rectilinear trajectory, having acquired a kick speed V

kick

in a random

direction in the orbital plane.

The ﬁrst quantitative analysis of this process was performed by Fitchett (1983), who

evaluated the lowest-order multipole moments for a Newtonian point-mass binary to obtain

the emitted linear momentum. He ﬁnds that the kick speed is approximately

kick

≈ 1480 km/s

f (q)

max



term



(13.5)

where q = m

≤ 1 is the mass ratio, M = m

+ m

is the total mass, and r

term

is the

binary separation at which the linear momentum emission terminates.

The function f (q)

is given by

f (q) = q

1 − q

(1 + q)

(13.6)

and assumes a maximum of f

max

 0.0179 at q = (3 −

√

5)/2  0.38. The kick speed

vanishes both for equal-mass binaries (q = 1) and in the test-particle limit, q = 0, as one

would expect. Assuming that r

term

may come close to the gravitational radius 2M,the

above expression predicts large kick speeds that easily exceed 1000 km/s. However, later

analytical estimates, based on perturbation theory or post-Newtonian calculations, revised

the maximum kick speed to smaller values of at most a few hundred km/s.

With the availability of numerical codes that can simulate the inspiral and coalescence of

binary black holes, it is possible to compute the recoil kick speed without approximation.

The ﬁrst such attempt was carried out by Herrmann et al. (2007a),whousedverycrude

initial data. The ﬁrst accurate calculation was presented by Baker et al. (2006b), who found

a kick speed of 105 ± 10 km/s for a mass ratio of q = 0.67.

A more comprehensive and very accurate study has been carried out by Gonz

alez

et al. (2007). The computational methods used in these simulations are similar to those

of Campanelli et al. (2006)andBaker et al. (2006a) described above; in particular they

use the moving puncture method to model the black holes (see Section 13.1.3), the BSSN

Favata et al. (2004).

cf. exercise 13.3 below.

See, e.g., Kidder (1995); Favata et al. (2004); Blanchet et al. (2005); Damour and Gopakumar (2006); Sopuerta et al.

(2007).

While Baker et al. (2006b) was published in a journal before Herrmann et al. (2007a), the latter appeared on the

xxx.arXiv.org preprint server approximately two month before the former.

13.2 Binary black hole inspiral and coalescence 449

300

200

100

(km/s)

∆v

(km/s)

∆v

(km/s)

100

−100

100

200

t(M

ADM

)

t(M

ADM

)

t(M

ADM

)

t(M

ADM

)

300

−200

−300

(h1-h2) (h1-h2)

1.45858*(h2-h3) 1.45858*(h2-h3)

100 200 300

−20

−40

100 200 300

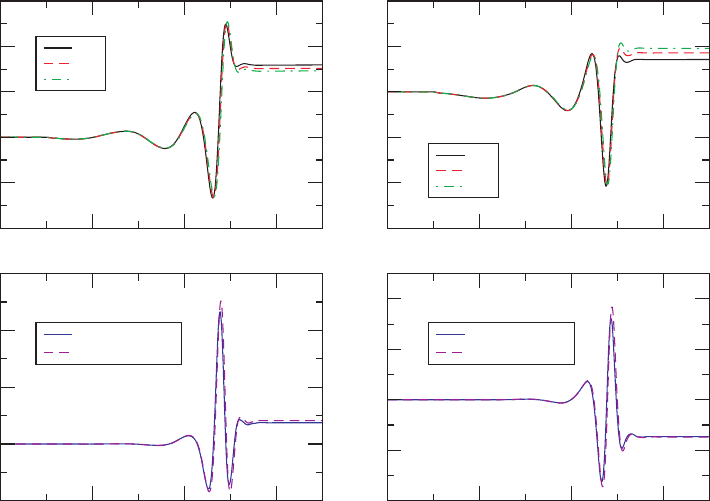
Figure 13.10 Components of the kick velocity as a function of time in the simulations of Gonz

alez et al. (2007)

for a nonspinning binary of mass ratio q = 0.33. The graphs show results for three different resolutions, the

ﬁnest of which are h

= m

/45, h

= m

/51, and h

= m

/58, where m

is the smaller black hole’s irreducible

mass. The convergence test in the lower panels demonstrates second-order convergence. As expected, the kick

velocity oscillates during the inspiral, and then remains constant once the emission of linear momentum ceases.

[From Gonz

alez et al. (2007).]

formulation of Einstein’s equations (Chapter 11.5), and an AMR grid structure.

Gonz

alez

et al. (2007) construct puncture initial data (see Chapter 12.2) describing unequal mass

binaries, ﬁxing binary parameters as obtained in post-Newtonian calculations. These initial

data contain some small amount of spurious gravitational radiation, which propagates

off the numerical grid via an initial pulse. Once this pulse has passed, integration of

equation (9.132), yields the kick momentum P

. In the calculations of Gonz

alez et al.

(2007), the Weyl scalar ψ

is extracted at r

ext

= 50M.

In Figure 13.10 we show the x and y components of the kick velocity V

kick

for a binary

of mass ratio q = 0.33, calculated from the components of the momentum P

by dividing

by the ﬁnal remnant black hole mass. The z component vanishes identically, since it would

describe motion perpendicular to the orbital plane. As we would expect from our discussion

Details of this numerical integration, together with many code tests and benchmarks, can be found in Br

ugmann et al.

(2008).

450 Chapter 13 Binary black hole evolution

0.15

0.2

0.25

100

150

200

250

300

v (km/s)

Baker, et al

Campanelli

Damour and Gopakumar

Herrmann, et al

Sopuerta, et al

Blanchet, et al

Figure 13.11 The kick velocity as a function of the symmetric mass-ratio parameter η = q/(1 +q)

,whereq is

the ratio of irreducible masses. The line connecting the open circles, together with the dashed line marking a 6%

error, denote the results of Gonz

alez et al. (2007). Also plotted are the earlier numerical results of Baker et al.

(2006b), Campanelli (2005), Herrmann et al. (2007a), as well as the analytical results of Blanchet et al. (2005);

Damour and Gopakumar (2006); Sopuerta et al. (2007). [From Gonz

alez et al. (2007).]

above, the kick velocity initially oscillates with an increasing amplitude, until the remnant

experiences a ﬁnal kick during the black hole merger. Shortly after that the emission of

linear momentum ceases, leaving the remnant to coast with a net kick speed V

kick

in a

random direction in the orbital plane.

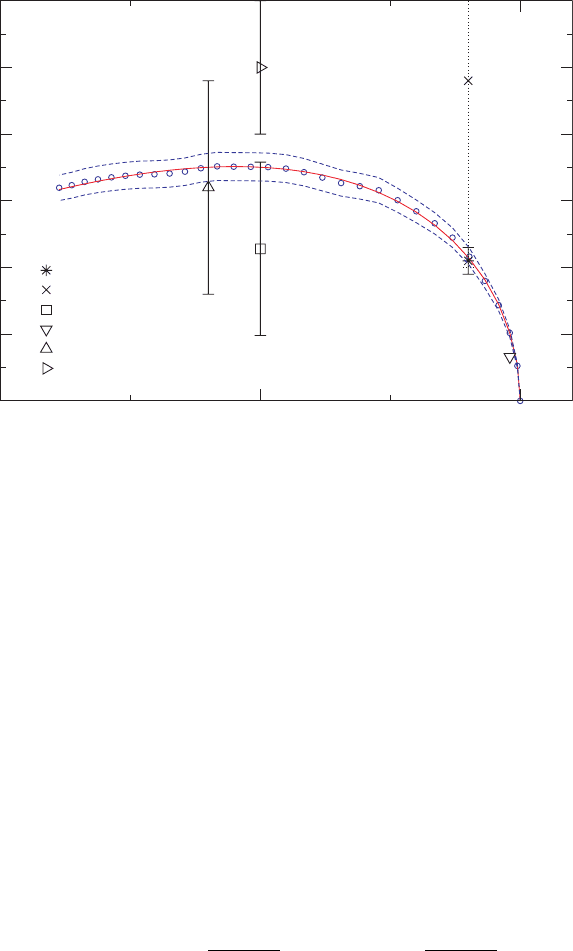
Figure 13.11 shows the ﬁnal kick speed V

kick

for a number of different mass ratios.

The maximum value of V

kick

= 175 ± 11 km/s is obtained for an irreducible mass ratio

of q = 0.36 ± 0.03.

Quite remarkably, this mass ratio is consistent with that of the

maximum value of Fitchett’s expression (13.5). In an extension of the work of Buonanno

et al. (2007), Berti et al. (2007) synthesized numerical calculations of the inspiral, merger

and ringdown of unequal mass binaries. In particular, they ﬁnd that the total energy E

emitted during the merger phase is approximately

E

/M = 0.032661

(1 + q)

+ 0.004458

(1 + q)

(13.7)

where M is the total initial ADM mass of the binary. Note that for equal-mass binaries with

q = 1 we recover a value close to the 3.5% that we stated in Section 13.2.1. Berti et al.

(2007) also ﬁnd that the angular momentum of the remnant black hole is well approximated

See also the simulation for q = 1/3 described in detail in Appendix I.