Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

13.1 Handling the black hole singularity 431

and axisymmetry (see Chapters 8 and 10). Ultimately, however, these coordinate systems

tend to develop “grid stretching” along black hole throats (see Chapter 8.1), another cause

of the premature demise of a numerical calculation.

For simulations of orbiting binaries in

three spatial dimensions it is even harder to identify singularity avoiding coordinates that

might lead to a long-term, stable evolution. As a consequence, most successful simulations

have adopted other strategies for avoiding spacetime singularities.

13.1.2 Black hole excision

The idea of black hole excision goes back to a suggestion by Unruh.

As long as cosmic

censorship holds, any spacetime singularity must be surrounded by an event horizon and

hence must reside inside a black hole. By deﬁnition, no information can propagate from

inside the black hole to the outside, so that none of the exterior spacetime can possibly be

affected by the black hole’s interior.

This suggests that it should be sufﬁcient to simulate

numerically only the exterior of any black holes, and to excise from the computational

domain any region that lies inside an event horizon. This approach is referred to as black

hole excision.

While the underlying idea of black hole excision is very elegant and transparent, some

of the details of its numerical implementation are more involved. To begin with, it is

usually not possible to locate an event horizon during a numerical simulation. It is usually

possible, however, to locate apparent horizons, which in general relativity are guaranteed

to lie inside event horizons.

In practice, therefore, it is the region interior to an apparent

horizon that is excised from the computational domain.

Excision itself can be implemented in different ways. In many applications all gridpoints

within a certain sphere (or ellipsoid) that lies within the apparent horizon are excised,

leaving only a small buffer zone of gridpoints just outside the sphere but inside the

apparent horizon on which valid data can reside.

Grid points within the excised region no

longer contain valid data and therefore cannot be used in equations to determine the values

of ﬁeld quantities in the black hole exterior. This means that the boundary of the excision

region has to be treated in a special way.

We point out another unappealing feature of singularity avoiding coordinate systems. By slowing down the advance

of proper time in areas close to a singularity, large amounts of computational resources are used to cover increasingly

small regions of spacetime. Adopting singularity avoiding coordinates may therefore lead to an uneconomical use of

the computational resources.

Unruh (1984), as quoted in Thornburg (1987).

See also the discussion in Chapter 7.1.

Some early numerical implementations include Seidel and Suen (1992); Scheel et al. (1995a); Alcubierre and Br

ugmann

(2001); Yo et al. (2002); Br

ugmann et al. (2004); Alcubierre et al. (2005); Pretorius (2005a,b).

See Chapter 7, and in particular the discussion in Chapter 7.1.

Recall, however, that in some slicings apparent horizons do not form, even though a black hole is present; see, e.g.,

exercise 8.10.

In Cartesian coordinates, the resulting excised region represents an approximation to the smooth sphere or ellipsoid,

and is often referred to as a “LEGO” sphere.

432 Chapter 13 Binary black hole evolution

Mathematically, no boundary conditions for the evolution equations should be required

on the excision surface, since all characteristics on that surface should be directed inward

(see Figure 6.1 and the surrounding discussion in Chapter 6.1). Numerically, however,

the excision surface may nevertheless require a special treatment. Many ﬁnite difference

applications, for example, use centered differencing (see Chapter 6.2), which, when applied

to a grid point on the surface, requires valid data on excised gridpoints. This problem can

be avoided quite simply, either by using one-sided difference stencils on the excision

surface,

or by extrapolating valid data to excised grid points from the outside before

these points are used in a centered differencing scheme.

When black holes move through a numerical grid, grid points that had previously been

excised may also re-emerge from a black hole, and have to be repopulated with valid

data. In many applications this is done by extrapolating from adjacent exterior points. We

will discuss some successful binary black hole simulations that have adopted black hole

excision in Section 13.2.1.

13.1.3 The moving puncture method

We have already encountered the puncture method in Chapter 12.2.2 for the construction of

black hole initial data. The key idea of the puncture method is to decompose the metric as

a sum or product of one term that contains the singularity, but is analytic, and a correction

term that must be obtained numerically, but is regular. In equation (12.50), for example,

we wrote the conformal factor ψ as a sum of the analytical black hole “punctures” 1/α

and a correction term u. We then found that the Hamiltonian constraint (12.52) becomes

a regular equation for u that can be solved everywhere, without any need for special

boundary conditions at the black hole or excision surface. Clearly, it is tempting to try a

similar approach for dynamical simulations containing black holes.

The ﬁrst attempts to construct such a scheme employed a “ﬁxed” puncture method. For

a single Schwarzschild black hole, for example, we could write the conformal factor as the

product

ψ =



1 +



f. (13.1)

Starting with initial data on a slice of constant Schwarzschild time we have f = 1 initially.

During the evolution, we could then leave the analytic singular part ﬁxed, and evolve

only the regular function f . In a binary evolution using this approach,

the singularities

remain at ﬁxed coordinate locations, given by the “punctures” in the analytical part of ψ.

That means that suitable gauge conditions have to be found that are consistent with this

prescription; i.e., the gauge conditions have to leave the singularities at their prescribed

coordinate locations and have to preserve the nature of their singular behavior, in this

See, e.g., exercise 6.5.

ugmann (1999).

13.1 Handling the black hole singularity 433

case a 1/r divergence. An additional complication arises from the fact that, under these

conditions, an evolution with a lapse that is positive everywhere cannot lead to a stationary

solution, even for a single Schwarzschild black hole.

As a consequence, binary black

hole simulations using the ﬁxed puncture method have not proven very successful, since

they have not led to long-term, stable evolution.

The breakthrough came with the so-called “moving” puncture method, ﬁrst suggested

independently by Baker et al. (2006a)andCampanelli et al. (2006).

In some sense the

moving puncture approach is even easier than the ﬁxed puncture approach. The singular

term in the metric is not factored out; instead, the metric is evolved in its entirety. The

puncture is allowed to move freely in accord with the gauge conditions, except that care is

taken that the singularity never hits an actual grid point. Usually this can be accomplished

quite easily. In situations that feature equatorial symmetry, for example, the punctures

always remain on the (orbital) plane of symmetry. Using a cell-centered ﬁnite difference

scheme

no grid points are located on this plane, so that the punctures can never encounter

a grid point. The moving puncture method is usually implemented in the BSSN formalism,

or some close adaptation. It is sometimes advantageous, in the context of this formalism,

to evolve a variable related to the inverse of the conformal factor, rather than the conformal

factor itself, since the inverse will vanish at puncture singularities rather than diverge.

With a suitable choice of gauge conditions, like the 1+log slicing condition (4.51) and the

Gamma-driver condition (4.83), this prescription leads to remarkably stable evolutions.

Before we summarize some of the details of the solution, we are compelled to address

one obvious question: how is it possible that the presence of puncture singularities in the

computational domain does not spoil the numerical calculations?

Considerable insight and clariﬁcation of this question has been provided by Hannam et al.

(2007, 2008)andBrown (2008). Consider the evolution of a single Schwarzschild black

hole. A puncture evolution of this spacetime could start out with initial data expressing

Schwarzschild geometry in isotropic coordinates at an instant of constant Schwarzschild

time. The conformal factor at this instant is then given by

ψ = 1 +

. (13.2)

As we have seen in Chapter 3, these isotropic coordinates do not penetrate the black

hole interior, but instead cover two copies of the black hole exterior. These two copies

represent a “wormhole” solution, i.e., two sheets of asymptotically ﬂat “Universes” that

are connected by an Einstein–Rosen bridge at the black hole horizon, as illustrated in

Figure 3.1. The singularity at isotropic radius r = 0, where the conformal factor diverges

Hannam et al. (2003); Reimann and Br

ugmann (2004).

Alcubierre et al. (2001); Br

ugmann et al. (2004).

See Br

ugmann et al. (2008)andHannam et al. (2008) for detailed discussions of this method, its numerical imple-

mentation, and geometrical interpretation.

See, e.g., Figure 6.2.

See van Meter et al. (2006) for a comparison of alternative gauge conditions for the evolution of moving punctures.

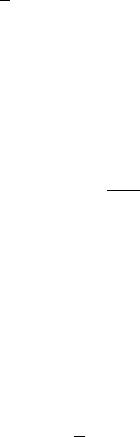
434 Chapter 13 Binary black hole evolution

as 1/r, corresponds to the asymptotically ﬂat end of the “other” Universe, and is therefore

a mere coordinate, and not a curvature, singularity.

Let us now evolve these initial data with the 1+log slicing condition (4.51),

∂

α − β

∂

α =−2αK (13.3)

and the Gamma-driver condition (4.83). These conditions are conditions on the time

derivatives of the lapse and shift only; before we can start the evolution we therefore

have to specify initial data for these variables. We could, for example, choose α = (1 −

M/(2r))/(1 + M/(2r)) and β

= ∂

= 0, which we recognize from the familiar static

form of the Schwarzschild line element in isotropic coordinates (equation 1.60). As we

discussed in the context of equation (2.162), these choices represent the Killing lapse

and shift; since they also satisfy the slicing conditions (4.51) and (4.83) with zero time-

derivatives, the resulting time evolution would leave all metric quantities time-independent

(see also equation 2.145 and the discussion that follows it). Consider instead the initial

choices α = 1andβ

= ∂

= 0. It is easy to see that these choices lead to a nontrivial

time evolution; speciﬁcally, the term D

α no longer cancels out the Ricci tensor α R

in equation (2.127), leading to a nonzero time-derivative of K

(see exercise 2.31).

Even though the spacetime geometry, which is still Schwarzschild, remains static, the

metric quantities now vary with time and thereby constitute a dynamical coordinate system.

Hannam et al. (2007) demonstrate that the solution behaves dynamically only for a brief

period, after which it settles down to a new, time-independent solution that is different from

the initial data. In particular, in the new, time-independent solution the conformal factor

is characterized by a 1/

√

r singularity at r = 0 instead of the original 1/r singularity. As

demonstrated in exercise 13.1, such a slice terminates on a (limit) surface of ﬁnite areal

radius r

Exercise 13.1 Assume a spherically symmetric spatial metric of the form γ

and assume that

ψ →



µM



1/2

as r → 0. (13.4)

Show that the surface r = 0 has an areal radius of r

= µM.

Consider, for a moment, evolving the data with a “nonadvective” version of the 1+log

condition (13.3), i.e., drop the shift term β

∂

α from that equation so that ∂

α =−2αK .The

late-time asymptotic solution, which is also time-independent, must satisfy ∂

α = 0, and

must then be maximally sliced with K = 0. This solution must therefore be a member of the

family of time-independent, maximal slicings (4.23)–(4.25), which are parametrized by C.

Hannam et al. (2007) provide numerical evidence that this late-time solution corresponds

to the particular member C = 3

√

/4, which has a limiting surface at r

= 3M/2. In

See the discussion following equation (3.20).

13.1 Handling the black hole singularity 435

r = ∞

r = M/2

r = 0

Figure 13.1 A schematic embedding diagram of a maximally sliced Schwarzschild geometry with

C = 3

√

/4 (for t = constant and θ = π/2; see equations 4.23–4.25). In contrast to the “wormhole” solution

shown in Figure 3.1, this “trumpet” solution has only one asymptotically ﬂat end, while the other end,

corresponding to r → 0, approaches an inﬁnitely long cylinder of areal radius r

= 3M/2. [After Hannam et al.

(2008).]

Appendix H we analyze this solution in more detail, and, in particular, we show that the

conformal factor for this solution indeed features a 1/

√

r singularity at the isotropic radius

r = 0, corresponding to an areal radius r

= 3M/2 (see equation H.8). In Figure 13.1

we sketch an embedding diagram for this solution, the appearance of which suggests

the name “trumpet” solution for this type of solution. For the “advective” version of the

1+log condition, only parts of the late-time solution can be constructed analytically (see

Appendix H), but qualitatively the results are very similar. In particular, the asymptotic

solution again features a “trumpet” geometry.

The key point is that the singularity at isotropic radius r = 0 is again a mere coordinate

singularity. Since the numerical grid terminates at r = 0andr

> 0, it does not include

the spacetime singularity at r

= 0. This result helps to explain in part the success of the

moving puncture method. In a nut-shell, it can be described as “excision-without-excision”;

instead of excising the spacetime explicitly as in the excision method, the moving puncture

method excises the innermost part of the black hole interior containing the spacetime

singularity with the help of a particular gauge choice.

Further insight into this behavior was provided by Brown (2008), who also performed

moving puncture simulations of Schwarzschild. Starting again with “wormhole” initial

data representing the Schwarzschild solution at an instant of constant Schwarzschild time,

he also evolved the data with the 1+log slicing condition (4.51)andα = 1 initially, but

chose different shift conditions. Evolving with zero shift, Brown (2008) points out that the

spatial slices, which start out connecting the two asymptotically ﬂat ends of the “wormhole”

solution, cannot possibly disconnect from either one of these two asymptotic regions. In

fact, for zero shift the solution has to remain symmetric across the Kruskal–Szekeres

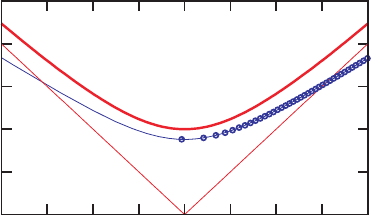
coordinate u = 0 at all times, as shown in Figure 13.2. All spatial slices remain connected

Hannam et al. (2008).

436 Chapter 13 Binary black hole evolution

III

21.510.50

− 0.5−1−1.5−2

2.5

1.5

0.5

Figure 13.2 The spatial slice at t = 3M in a moving puncture simulation of a single Schwarzschild black hole,

plotted in a Kruskal–Szekeres diagram. The solid blue line shows the slice that results from an evolution with

zero shift in equation (13.3), while the dots represent the location of individual grid points when evolved with the

Gamma-driver condition (4.83). The upper red line represents the spacetime singularity at r

= 0. [From Brown

(2008).]

to both asymptotic ends. But since the slicing condition (4.51) is independent of the

shift, the same result must hold for any other shift condition, including the Gamma-driver

condition (4.83). The only difference is that individual spatial coordinate locations, or

numerical grid points, now move on the spatial slices. For the Gamma-driver condition,

the grid points, marked by dots in Figure 13.2, move “away” from the “other” asymptotic

region very quickly, toward the right hand side in a Kruskal–Szekeres diagram. Even

for a very ﬁne grid resolution, and after only a very short time, no grid points remain

in region III of the diagram. It is in this sense that a dynamical evolution approaches

a “trumpet” solution like the one we discussed above. Even though the solutions have

different asymptotic behavior, the Gamma-driver condition moves all grid points into a

region where the two solutions converge towards each other.

Moreover, the grid points

drift safely away from the coordinate singularity at large negative u.

Figure 13.2 also illustrates that the spatial slices again do not encounter the black hole

spacetime singularity. In fact, these slices have properties similar to those of “singularity

avoiding” coordinates, except that the gauge conditions used in moving puncture simu-

lations avoid the coordinate pathologies (e.g., “grid stretching”) often encountered when

using other singularity avoiding coordinates.

13.2 Binary black hole inspiral and coalescence

In this section we will review some of the earliest successful simulations of binary black

hole inspiral and coalescence. In Section 13.2.1 we focus on the ﬁrst complete simula-

tions, which marked an important breakthrough in the numerical evolution of strong-ﬁeld,

We refer to Hannam et al. (2008) for a more detailed discussion.

13.2 Binary black hole inspiral and coalescence 437

vacuum spacetimes. These simulations were performed for equal-mass binaries with zero

spin. In Section 13.2.2 we will then discuss simulations of binaries containing black hole

companions with mass ratios different from unity and with nonzero spin, as well as the

calculation of black hole recoil. These results have important implications for black hole

astrophysics and gravitational wave astronomy.

13.2.1 Equal-mass binaries

The simulation of binary black hole inspiral, plunge and merger had been a long-standing

goal of numerical relativity. A vacuum problem in pure geometry, with no other compli-

cating sources or physical interactions, this two-body scenario remained one of the most

important unsolved problems in classical general relativity. In addition, theoretical tem-

plates of gravitational waveforms from binary black holes are of crucial importance for

the identiﬁcation and subsequent interpretation of such signals in the data of the new gen-

eration of gravitational wave interferometers. With the construction of these detectors, the

solution of the binary black hole problem had become very urgent. Nevertheless, solving

the problem, sometimes called the “holy grail” of numerical relativity, had resisted the

efforts of numerous researchers for many years. It is not surprising, then, that Pretorius’s

announcement of his successful simulation of a binary black hole inspiral and merger at a

workshop hosted by the Banff International Research Station in April 2005 was met with

great excitement.

Pretorius (2005a) uses the generalized harmonic formalism described in Chapter 11.3,

and eliminates black hole singularities with an excision method described in Section 13.1.2.

In his initial calculations Pretorius created a black hole binary from nonsingular initial data

by letting a scalar ﬁeld (see Chapter 5.4) undergo gravitational collapse. By boosting the

initial scalar ﬁeld conﬁguration, he generated a binary system in an approximate circular

orbit. The companions each then collapsed to black holes prior to merger. While these

calculations were not meant to simulate a realistic astrophysical scenario, they did provide

the ﬁrst calculation that could stably evolve a binary black hole from inspiral through

merger to ﬁnal ringdown, with the remnant settling down to a stationary Kerr black hole.

Figure 13.3 shows contours of the lapse function α in the orbital plane during one of

these simulations. In these calculations, Pretorius adopts a compactiﬁed coordinate system

in which the outer boundaries correspond to spatial inﬁnity. He also uses adaptive mesh

reﬁnement (AMR, see Chapter 6.2.5) to achieve sufﬁcient grid resolution close to the black

holes. In his original calculations, the ﬁnest resolution is placed in the vicinity of each

black hole and is approximately M/20.

In later work, Pretorius replaced the scalar ﬁeld initial data with conformal thin-

sandwich, binary black hole initial data as described in Chapter 12.3.

This choice

signiﬁcantly reduces the eccentricity of the resulting orbit and allowed Pretorius to follow

Here and below M is the total intial ADM mass of the binary system.

Speciﬁcally, he used the initial data of Cook and Pfeiffer (2004)andCaudill et al. (2006).

438 Chapter 13 Binary black hole evolution

t=30 M

0.50 1.00

t=321 M

0.50 1.00

t=80 M

0.50 1.00

t=114 M

0.50

1.00

t=115 M

0.50 1.00

t=129 M

0.50 1.00

Figure 13.3 Evolution of the lapse function α in the orbital plane during the merger of an equal-mass,

nonspinning binary black hole in the calculation of Pretorius (2005a). The black regions are the excised domains

in the black hole interior. The apparent horizons merge between the times of 114M and 115M,whereM is the

total initial ADM mass of the binary, and the initially distorted remnant subsequently settles down to an

axisymmetric stationary Kerr black hole. [From Pretorius, private communication.]

the inspiral for several orbits prior to merger.

In Figure 13.4 we plot the orbital evolution

of such an equal-mass binary, together with the location of the apparent horizons at several

key instants of time.

Pretorius’ success was quickly followed by another breakthrough that employed a com-

pletely independent approach. Both Campanelli et al. (2006)andBaker et al. (2006a)

adopted versions of the BSSN formalism described in Chapter 11.5, together with the

moving puncture approach of Section 13.1.3, and were also able to follow binary black

hole coalescence through merger to ringdown.

The original implementations of Campanelli et al. (2006)andBaker et al. (2006a)differ

in some of the details. Baker et al. (2006a) use the BSSN formalism and the moving

puncture approach very similar to our descriptions in Chapter 11.5 and Section 13.1.3.

As did Pretorius, they also use AMR to achieve sufﬁcient grid resolution. Campanelli

et al. (2006) implement a slight variation of the BSSN formalism. Instead of evolving the

conformal exponent φ in the standard BSSN formulation (see equation 11.46), they evolve

the inverse of the conformal factor, χ = exp(−4φ), which vanishes at the punctures.

Given suitable gauge conditions it is possible, with this choice, to keep all quantities

regular during the evolution. This approach has the advantage that the punctures may now

encounter grid points without causing numerical difﬁculties. Also, Campanelli et al. (2006)

See Buonanno et al. (2007).

13.2 Binary black hole inspiral and coalescence 439

−4 −2

024

−4

−2

initial pre-merger AH shapes

final pre-merger AH shapes

initial enveloping AH shape

late time AH shape

est. late time corotating light ring

Figure 13.4 The evolution in the orbital plane of an equal-mass, nonspinning binary black hole, showing the

coordinate locations of the apparent horizons (AH) at several key moments during the inspiral and merger. [From

Buonanno et al. (2007).]

adopt a uniform numerical grid (as opposed to AMR), but introduce “multiple transition

ﬁsheye” spatial coordinates

as well as fourth-order ﬁnite differencing to provide sufﬁcient

resolution for the black holes. In many of the other aspects the two approaches are very

similar. In particular, both Campanelli et al. (2006)andBaker et al. (2006a) adopt the

puncture initial data described in Chapter 12.2 – a natural choice for evolution with the

moving puncture method – to describe a quasiequilibrium binary conﬁguration close to

the ISCO.

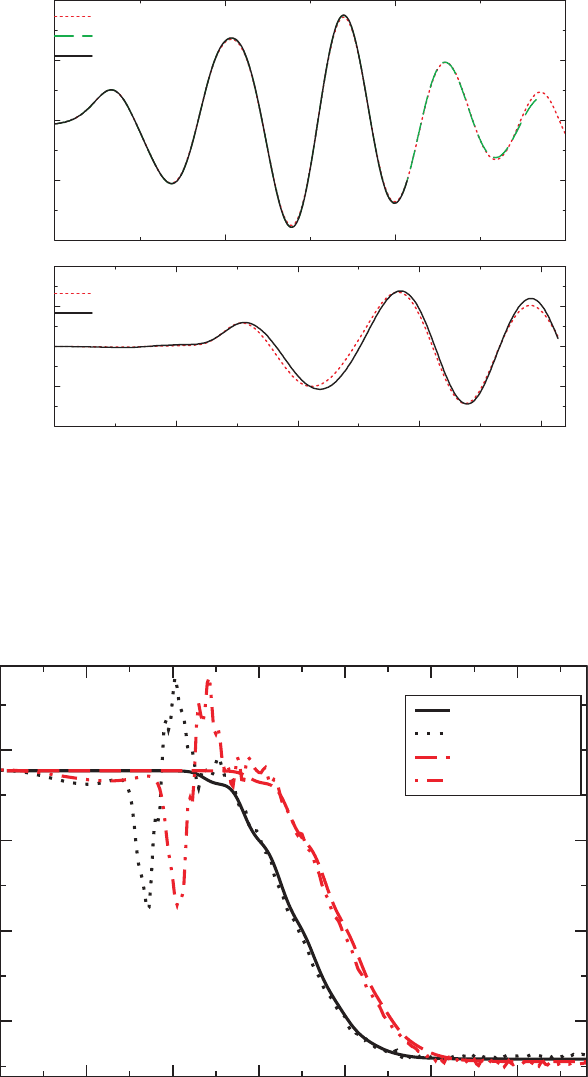
Figures 13.5 and 13.6 illustrate some of the results of Campanelli et al. (2006)and

Baker et al. (2006a). Figure 13.5 shows the gravitational waveform Re(ψ

) (i.e., the real

part of the Newman–Penrose scalar ψ

, see Chapter 9.4.2)ofCampanelli et al. (2006). In

this particular calculation the grid extends to an outer boundary of 60M, and Re(ψ

)is

extracted at 5M.

The calculation is then performed with three different grid resolutions,

x = M/16, M/24, and M/36 in the innermost region, where the resolution is the ﬁnest.

The comparison of results suggests that the simulation is fourth-order accurate, as expected

from a fourth-order ﬁnite difference implementation (see Chapter 6.4).

See Chapter 14.2.3 for a brief description.

To obtain waveforms measured by a distant observer, one must extract them at a much larger separation from the

binary. In this implementation, however, the waveforms are affected by the outer boundaries. Consequently, for the

purposes of the convergence test plotted in this ﬁgure, Re(ψ

) is determined at a smaller radius, so that it remains

causally disconnected from the outer boundary until a later time.

010203040

t/m

−0.0004

−0.0002

0.0002

0.0004

(M/16) ψ

(M/24)

(ψ

(M/24) ψ

(M/36))

(81/16)

0204060

−0.02

−0.01

0.01

0.02

(Re part of (l=2,m=2))

M/16

M/24

M/36

−

Figure 13.5 The gravitational waveform Re(ψ

) for an equal-mass, nonspinning binary black hole merger in the

calculation of Campanelli et al. (2006). Results are plotted for different grid resolutions. This convergence test

suggests fourth-order convergence, as expected from a fourth-order ﬁnite difference implementation. [From

Campanelli et al. (2006)].

02040

80 100 120

0.98

0.99

1.01

M - E, r

=40M

ADM

, r

=40M

M - E, r

=50M

ADM

, r

=50M

Figure 13.6 Demonstration of energy conservation in the calculation of Baker et al. (2006a). The initial total

energy (the initial total ADM mass) M minus the energy E carried off in gravitational radiation agrees with the

instantaneous total energy M

ADM

to high accuracy. [From Baker et al. (2006a).]