Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

17.1 Initial data 571

0.08 0.1 0.12 0.14 0.16 0.18

Ω

tid

Mass ratio (

irr

/ M

ADM,0

)

= 0.12

= 0.13

= 0.14

= 0.15

= 0.16

= 0.17

Figure 17.3 The tidal break-up limit. The lines represent the estimate (17.17) with A = 0.27 for different

neutron star compactions, while the other symbols show the corresponding numerical results. The quantity

denotes the dimensionless (baryon) rest mass of the neutron star and is larger for higher compactions; the

maximum isolated mass corresponds to

= 0.18. [From Taniguchi et al. (2008).]

the tidal separation is larger than the ISCO separation, i.e., if the compaction is sufﬁciently

small, the neutron star breaks apart before encountering an ISCO. The post-Newtonian

curve cannot capture this behavior, since it ignores the neutron star’s internal structure.

Finally, we note that the “leading-order spin approximation”, which amounts to setting



spin

to the orbital angular speed in the boundary condition (17.13), evidently introduces

some numerical error. This curve shows a larger deviation from the post-Newtonian result

than the corresponding curve for which the black hole’s quasilocal spin is set to zero, and

the minimum in the binding energy no longer coincides with a minimum in the angular

momentum – exactly as for the nonspinning black hole binaries of Chapter 12.4.

It is of interest to see how well the estimate (17.3) predicts the actual numerical results.

Instead of expressing the latter in terms of the binary separation, which is a gauge-

dependent quantity, it is more natural to parametrize the separation in terms of the orbital

angular speed .Inequation(17.3) we can eliminate r

tid

with the help of Kepler’s law





+ M

(17.16)

(where equality holds for Newtonian point masses). Combining equations (17.3)and

(17.16)weﬁnd



tid

= A





3/2



1 + q



1/2

, (17.17)

where

A is a yet-to-be-determined constant of order unity.

In Figure 17.3 we show a comparison between the estimate (17.17) and the actual

numerical results for a number of different neutron star compactions M

. Choosing

572 Chapter 17 Binary black hole–neutron stars

A = 0.27 in the estimate (17.17) captures the numerical tidal break-up results rather well,

although we caution that these results cover only a very small part of parameter space – and,

in particular, only n = 1 polytropes. Using equation (17.17) to estimate the characteristic

gravitational wave frequency f

= /π at tidal break-up yields

 730 Hz



1.4M





1/2



15 km



−3/2



(1 + q)/q

4/3



1/2

. (17.18)

As mentioned earlier, this frequency resides within the LIGO band.

Having identiﬁed

A = 0.27 in equation (17.17), we can now reﬁne equation (17.3)to

obtain

tid

 2.4 q

−2/3

. (17.19)

Assuming a typical neutron star compaction of M

 0.15 we can now estimate the

critical mass ratio at which tidal separation occurs at the ISCO by setting the left-hand side

of equation (17.19) equal to r

ISCO

 6, which yields

crit

 4. (17.20)

Evidently, neutron stars are tidally disrupted only in binaries with black holes of comparable

mass. The tidal disruption of the neutron star and the subsequent formation of a gaseous

disk may be necessary ingredients for a GRB model based on the merger of a black

hole–neutron star binary. As these estimates suggest, and as we discuss in greater detail

in Section 17.2, it is difﬁcult to form such a disk for nonspinning black holes. For rapidly

rotating black holes, however, the ISCO occurs at a smaller binary separation, enhancing

the possibility of tidal break-up and the formation of a disk.

17.1.2 The conformal transverse-traceless approach

Shibata and Ury

u (2006, 2007) adopt an alternative approach to construct black hole–

neutron star binaries. Instead of using the conformal thin-sandwich decomposition of the

Einstein’s constraint equations, as in the previous section, they employ the conformal

transverse-traceless decomposition to construct the extrinsic curvature.

Following Chapter 3.2, we can split

into a transverse-traceless piece and a longitudi-

nal piece. We may assume the former to vanish, and write the latter as the vector gradient

of a vector W

= (

LW)

(17.21)

(see equation 3.50). Assuming maximal slicing K = 0, the momentum constraint then

reduces to

(



W )

= 8πψ

(17.22)

17.1 Initial data 573

(see equation 3.53). Given the linear nature of this equation, we can write its solution as

the sum of a particular and a homogeneous solution. We may choose the latter, which

satisﬁes the homogeneous equation

= 0, to describe the black hole, in which case

the former accounts for the neutron star only.

As in Chapter 12.2, where we constructed binary black holes in exactly the same way,

we may adopt conformal ﬂatness ¯γ

= η

and take the boosted Bowen–York black hole

solution (3.80) as the homogeneous solution



+ P

− (η

− n



. (17.23)

The coordinate distance r from the black hole’s center and the normal vector n

are

deﬁned in the context of equation (3.80) (see also Chapter 12.2.1), and for circular orbits,

the momentum P

of this solution has to point in a direction perpendicular on the axis

connecting the black hole and the center of the neutron star (see Chapter 12.2.3). This

analytical homogeneous solution to equation (17.22) then accounts for the black hole of

the black hole–neutron star binary.

Given a matter source S

, we can now solve equation (17.22) with appropriate asymptotic

fall-off boundary conditions to ﬁnd the neutron star contribution

. This can be done

by solving equation (17.22)forW

, using one of the decompositions of W

described in

Appendix B, and then computing

from equation (17.21). Adding this result to the

black hole contribution yields

. (17.24)

We can now insert this extrinsic curvature into the Hamiltonian constraint (17.4), which,

given the matter source ρ, we can solve via the “puncture” method (12.50) described in

Chapter 12.2.2. This completes the construction of the initial data, assuming we know the

matter sources ρ and S

Of course, we do not know these matter sources a priori. Instead, we need to determine

them self-consistently with the gravitational ﬁeld variables, so that they describe the neutron

star in quasiequilibrium circular orbit about its black hole companion. This determination

entails solving the ﬂuid equations above, either equation (17.8) for corotating stars, or

equations (17.10) and (17.11) for irrotational stars. Since the notion of an equilibrium

ﬂuid ﬂow involves a condition on the ﬂuid 4-velocity u

, i.e., a 4-dimensional object, it

is clear that we need information about the spacetime not only on the initial slice, but in

a neighborhood of this slice. This observation is one of the reasons why the conformal

thin-sandwich decomposition, which automatically introduces the lapse and shift that are

needed in the above ﬂuid equations, is more commonly used for the construction of

quasiequilibrium ﬂuid initial data (see also the discussion in Chapter 15.2).

The conformal transverse-traceless decomposition, by contrast, only provides the metric

and extrinsic curvature of the initial slice, meaning that we now need to construct a lapse

and shift independently. This cannot be just any lapse and shift, of course – instead they

574 Chapter 17 Binary black hole–neutron stars

must describe the coordinate system in which the binary appears momentarily stationary, as

assumed in the derivation of the ﬂuid equations. In other words, we require the 4-velocity of

the resulting coordinate-observer to be aligned with the approximate helical Killing vector

describing the binary orbit. We can construct such an approximate “Killing” lapse and shift

by solving equations (17.5) and (17.6) of the conformal thin-sandwich decomposition.

Unlike we did in the previous section, however, we do not express

in these equations in

terms of the shift as in equation (17.7), but instead use the transverse-traceless expression

(17.24). The latter is based on equation (17.21) instead of equation (17.7), and does not

result from, and therefore does not self-consistently embody, the assumption of a helical

Killing vector. In this case, the solutions of equations (17.5) and (17.6) do not require

excision: all terms in equation (17.5) are regular, and the singular terms in equation (17.6)

can be treated analytically by writing

αψ = 1 +

+ v (17.25)

in complete analogy to the puncture approach (12.50) for the conformal factor.

The

resulting equation for the new variable v is then regular, and the constant C can be

determined by imposing a virial relation, namely by equating the Komar mass (3.179) with

the ADM mass (3.145) as in equation (12.108).

Given the lapse and shift, we can ﬁnally solve the ﬂuid equations, which in turn provide

the matter sources ρ and S

in equations (17.4) and (17.22). A self-consistent solution

can then be found by solving all of the above equations iteratively until convergence has

been achieved. These solutions have been used as initial data for dynamical simulations,

which we will describe in Section 17.2.2 below.

17.2 Dynamical simulations

17.2.1 The conformal ﬂatness approximation

The merger of a black hole-neutron star binary, focusing on the tidal disruption of the

neutron star, has been investigated in a number of Newtonian

and semirelativistic sim-

ulations.

Some of the ﬁrst dynamical simulations of merging binaries that attempted

to evolve the black hole–neutron star spacetime self-consistently in a general relativistic

framework were performed by Faber et al. (2006a,b) in the conformal ﬂatness approxima-

tion. We have already discussed in Chapter 16.2 the application of this approximation to

track binary neutron star mergers. However, the conformal ﬂatness approximation is not

cf. Tichy et al. (2003).

See also Hannam et al. (2003); Tichy et al. (2003); Hannam and Cook (2005); Hannam (2005).

Shibata and Ury

u (2006, 2007); Shibata and Taniguchi (2007); Yamamoto et al. (2008).

See, e.g., Lee and Klu

zniak (1999); Janka et al. (1999); Rosswog (2005).

See, e.g., Rantsiou et al. (2007), who studied merging black hole–neutron star systems with high mass ratios q ∼10

by evolving neutron stars in a ﬁxed Kerr background metric, treating the self-gravity of the matter by a Newtonian

potential in the hydrodynamic equations.

17.2 Dynamical simulations 575

well suited to handle an arbitrary black hole–neutron star spacetime since it contains a

moving, vacuum black hole containing an interior singularity. The metric ﬁeld equations

in the conformal approximation are not evolution equations but spatial elliptic equations,

identical to the conformal thin-sandwich equations (17.4)–(17.6) used to solve the initial

value problem. Consequently they do not involve time and cannot be used to determine the

motion of the black hole or track the changing position of its interior spacetime singularity.

Nor can these ﬁeld equations encounter the singularity without blowing up. The one limit

in which the conformal approximation can be applied to the binary black hole–neutron

star problem is the case in which the black hole mass is considerably larger than the mass

of the neutron star. In this situation, the black hole remains nearly ﬁxed in space and the

spacetime near the black hole is dominated by the massive hole. This limit enables one to

determine the metric by avoiding the black hole singularity while still accounting for the

strong-ﬁeld contributions from both the black hole and neutron star matter.

Consider the Hamiltonian equation (17.4) used to solve for the conformal factor ψ.

Embed the neutron star in a computational spatial domain whose characteristic size d

satisﬁes M

 d  M

. Exploiting this inequality makes it possible to construct a

computational grid that encompasses the neutron star matter but avoids the black hole

horizon. Decompose ψ according to ψ = ψ

+ ψ

,whereψ

= 1 + M

/2r may be

taken to be the exact solution for a stationary, isolated, nonspinning Schwarzschild black

hole in isotropic coordinates as a function of the radius from the black hole. Since ∇

0, equation (17.4) results in a nonlinear elliptic equation for ∇

. This equation can

be solved on the computational grid by considering all the source terms inside the grid

interior and imposing suitable asymptotic conditions on ψ

at the outer boundary of

the grid, where ψ

falls off to zero. The resulting metric solution for ψ then accounts

self-consistently for the ﬁeld that arises from the combined nonlinear contributions of the

black hole and the neutron star matter sources inside the grid. The (small) contribution

from ψ

in the region outside the computational grid can be obtained analytically by a

suitable multipole expansion involving multipole moments of the interior source. As long

as the metric outside the computational grid is dominated by the black hole, the solution

remains roughly valid even if some of the matter ﬂows out into this region. The solutions

to the lapse and shift equations are obtained by similar considerations.

The approach described above was developed by Faber et al. (2006a) to handle binaries

with large black hole-to-neutron star mass ratios in conformal gravitation. They used a

spheroidal spectral routine based on the LORENE code to solve the ﬁeld equations and a

relativistic SPH code to evolve the hydrodynamics.

Subsequently, Faber et al. (2006b)

switched to an FFT convolution-based scheme to solve the ﬁeld equations, whereby they

linearized the nonlinear terms in the Hamiltonian about a previous guess for ψ

and

iterated until convergence. The SPH approach for the hydrodynamics has the advantage

See Chapter 16.2, where similar tools were used for the treatment of binary neutron star mergers in the conformal

approximation.

576 Chapter 17 Binary black hole–neutron stars

that, given the metric ﬁeld, SPH does not require a grid on which to evolve the matter, hence

the matter can be followed everywhere, even in the region in exterior to the computational

grid constructed to solve the ﬁeld equations.

For initial data Faber et al. (2006b) consider both corotational and irrotational neutron

star companions, modeled as polytropes.

One of the goals of Faber et al. (2006b)isto

delineate regimes of stable vs. unstable mass transfer and to identify the point of onset

of tidal disruption for different neutron star compactions, EOS stiffness, and binary mass

ratios. Their simulations reveal that whenever mass transfer begins while the neutron star

orbit is still outside the ISCO the transfer is more unstable than predicted by earlier analytic

formalisms. The reason is that mass transfer causes the orbital separation to increase and

the neutron star radius to expand, both on a dynamical time scale. Models of mass transfer

that assume the orbit remains quasicircular are thus not applicable. The unstable mass loss

drives the evolution of the binary orbit and leads to the disruption of the neutron star in a

few orbital periods. Most of the mass is accreted promptly by the black hole. Some matter

is shed outward, becomes gravitationally unbound and is ejected from the system. The

remaining matter forms an accretion disk around the black hole.

As a representative example, Faber et al. (2006b) consider the evolution of an irrota-

tional binary in which the mass ratio is q = M

= 10, the neutron star compaction

is M

= 0.09 and the polytropic index is n = 1. The initial separation is chosen

to be r/M

= 5.5, just outside the ISCO at r

ISCO

≈ 5 in the adopted (isotropic)

coordinates. The initial data for this simulation describe a relativistic, irrotational BHNS

model calculated in the conformal thin-sandwich formalism by Taniguchi et al. (2005).

According to equation (17.19) the tidal break-up radius is at r

tid

≈ 5.8. Not surpris-

ingly, the simulation shows that tidal disruption occurs. Rapid angular momentum transfer

during the disruption ejects a signiﬁcant fraction of the matter back outside the ISCO, part

of which forms an accretion disk.

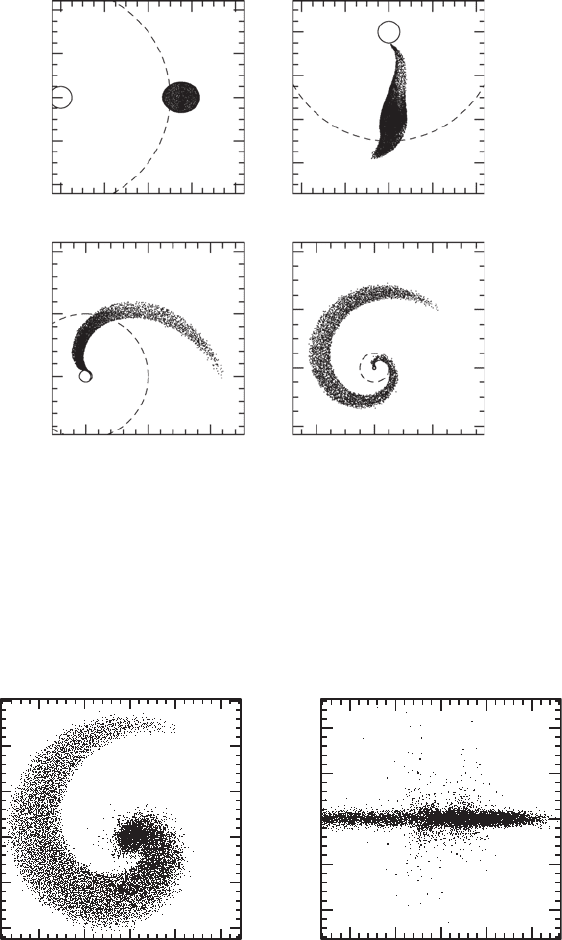
The simulation is depicted in Figures 17.4 and 17.5. The rapid redistribution of angular

momentum during the tidal disruption of the neutron star near the ISCO causes an outwardly

directed spiral arm to form, sending some of the matter outside the ISCO. By the end of

the simulation, the black hole accretes ∼75% of the total neutron star rest mass, while

∼12% of the matter forms a disk and ∼13% is ejected completely from the system. Here

bound and unbound matter trajectories are distinguished by the sign of u

+ 1, where u

is the time component of the matter 4-velocity. Note that the quantity u

remains nearly

constant in time for the (low pressure) outﬂowing gas streaming along quasigeodesic

worldlines in the nearly static spacetime that forms following the accretion of the bulk of

the disrupted star. The bound matter in the disk, while cold at ﬁrst and ejected into the

Neutron star binaries are likely to be irrotational since the magnitude of the viscosity required to synchronize the stars

is unphysically large (Bildsten and Cutler, 1992; Kochanek, 1992a). By the same reasoning, typical black hole–neutron

star binaries are also likely to be irrotational, since the required viscosity to synchronize a neutron star increases as the

primary mass increases.

see Chapter 17.1 for discussion.

17.2 Dynamical simulations 577

t /M

= 0

t / M

= 200

t / M

= 262

x / M

y / M

t /M

= 168

510

−20

−2

−4

−6

Figure 17.4 Snapshots of the disruption of a neutron star at selected times, projected into the orbital plane of the

black hole–neutron star binary, as computed assuming conformally ﬂat gravitation. The neutron star is an n = 1

polytrope with a compaction at inﬁnite separation of M

= 0.09; the binary mass ratio is M

= 10.

The neutron star, represented by approximately 60 000 SPH particles, disrupts near the ISCO (dashed curve) to

produce a mass-transfer stream that eventually wraps around the black hole horizon (solid curve) to form a torus.

The initial orbital period is P/M

= 105. [After Faber et al. (2006b).]

100

−50

−100

200

300

100

x/M

y/M

z/M

−100

−200

Figure 17.5 Snapshots of the same simulation depicted in Figure 17.4 at late time, t/M

= 990, projected

onto the orbital (left panel) and meridional (right panel) planes. A hot torus at r/M

∼

50 is evident. Bound

ﬂuid elements satisfying u

+ 1 < 0 are shown as heavy dots, unbound elements as light dots. [From Faber et al.

(2006b).]

578 Chapter 17 Binary black hole–neutron stars

spiral arm without strong shock heating, eventually undergoes shock heating as it falls

back and wraps around the black hole forming a torus. The torus extends to a radius

r/M

∼50 within a time t/M

∼1000 (corresponding to ∼0.07s for typical neutron

star masses). The characteristic temperature in the inner part of the torus is estimated to

be T ∼3 − 10 MeV ∼ (2–7) × 10

K. Faber et al. (2006b) point out that this system is a

plausible model for the central engine of a short-hard GRB. Among its other attributes, a

funnel is cleared out along the polar axis along which a GRB jet can presumably propagate

(no “baryon pollution”). Also, the high temperatures can produce an appreciable thermal

neutrino luminosity, L

∼ 10

ergs

−1

, which in turn can produce an appreciable electron

pair annihilation luminosity required by some GRB models to generate the observed

gamma-ray ﬂux.

However, there are other scenarios involving neutron stars and compact

binary mergers that are possible progenitors of short-hard GRBs.

We have thus seen that the main virtue of binary black hole–neutron star simulations

in conformal gravitation is that, to ﬁrst approximation, they can track the bulk motion of

matter in a relativistic gravitational ﬁeld, at least in the case when the black hole-to-neutron

star mass ratio is large. In particular, such similations can follow the tidal-break up of the

neutron star by a black hole when break-up occurs, and they can trace the subsequent

dynamical ﬂow of the matter, including possible disk formation about the black hole. But

since the spatial metric is restricted to be conformally ﬂat, the simulations described here

are only qualitatively reliable at best. In particular, the predictions of disk masses and

ejected mass fractions are not very trustworthy, especially when the black hole is rapidly

spinning. Moreover, because the metric is not dynamical, these simulations do not convey

any direct information about the emitted gravitational wave content of the spacetime.

At best, information about gravitational waves can be estimated by evaluating the wave

components of the metric perturbatively, after the simulation is completed. We did this in

Chapter 16.2 for binary neutron stars when we adopted the quadrupole approximation to

calculate gravitational waveforms. Here we shall postpone a discussion of the gravitational

waves generated by black hole–neutron star mergers to the next section, where we will

describe fully relativistic treatments of the evolution.

17.2.2 Fully relativistic simulations

As we mentioned earlier, simulations of binary black hole–neutron star mergers provide the

ultimate challenge of evolving compact binaries in full general relativity: they involve all of

the complications of relativistic hydrodynamics, including shocks, in a strong, dynamical

See, e.g., Aloy et al. (2005); Piran (2005) and references therein.

For high-mass binary neutron stars containing unequal mass companions with q ∼ 0.7, prompt collapse to a black

hole following merger also leads to the formation of a substantial, hot, neutrino-radiating accretion disk for which

the polar axes are also free of intervening matter (Shibata and Taniguchi, 2006). However it is not clear whether such

unequal mass binaries exist, since all observed systems containing pulsars that yield reliable mass measurements have

∼

0.9. Lower-mass binary neutron stars produce hypermassive neutron stars upon merger which undergo delayed

collapse to a black hole. Simulations show that substantial, hot accretion disks with collimated magnetic ﬁelds are also

formed in this case, so hypermassive neutron stars are also possible progenitors of short-hard GRB central engines.

See Chapters 14 and 16 and Figure 16.12 for more extensive discussion.

17.2 Dynamical simulations 579

ﬁeld, together with all of the hurdles of tracking moving black holes without encountering

their interior spacetime singularities. It is not surprising that progress in this area has been

achieved by adapting and extending many of the tools and techniques used to evolve binary

black holes and binary neutron stars. In this section we will summarize some of the earliest

simulations that have tackled this problem successfully.

Corotational neutron stars and nonspinning black holes

Shibata and Ury

u (2006, 2007) performed some of the earliest simulations of black hole–

neutron star mergers in full general relativity. Their initial data consist of corotational

neutron stars in quasiequilibrium circular orbit about nonspinning black holes and are deter-

mined using the conformal transverse-traceless approach discussed in Section 17.1.2.

The black hole is modeled by a moving puncture with no spin and the neutron star by a

-law EOS, with  = 2 (i.e., polytropic index n = 1), and a corotating velocity ﬁeld. The

approach of treating the black hole by moving punctures, which has worked so well in

the case of vacuum binary black hole mergers (see Chapter 13.1.3), again proves to be a

robust technique for tracking the motion and determining the evolution of the black hole

without enountering singularities. Handling a moving black hole puncture in the presence

of relativistic matter turns out to be straightforward. In fact, the ability of the moving

puncture method to incorporate matter without imposing black hole excision has been

bolstered by independent test-bed simulations.

The evolution code employed by Shibata and Ury

u (2006, 2007) is based on the BSSN

scheme for the gravitational ﬁeld, with a few reﬁnements, and an HRSC scheme for the

hydrodynamic matter. One of the reﬁnements concerns the function φ appearing in the

BSSN conformal factor (recall equation 11.46). They choose to evolve φ

−6

instead of φ,

since φ diverges at the puncture.

Note, however, that for the binaries considered here, the

location of the puncture remains in the orbital plane and, with a cell-centered Cartesian

grid, never encounters a grid point.

Exercise 17.2 Show that the evolution equation for φ

−6

∂

−6

= ∂

(φ

−6

) + (α K − 2∂

)φ

−6

. (17.26)

Another reﬁnement deals with the handling of the advective terms in the ﬁeld evo-

lution equations, which have the form (∂

− β

∂

)Q,whereQ is one of the ﬁeld vari-

ables. Shibata and Ury

u (2006, 2007) recast these terms in “conservative” form as

See L

ofﬂer et al. (2006) for simulations in general relativity of head-on collisions between neutron stars and black

holes of comparable mass.

See, e.g., Faber et al. (2007), who treat relativistic Bondi accretion onto a moving black hole puncture to test their

algorithm.

Campanelli et al. (2006)andBaker et al. (2006a) employed a similar substitution for handling puncture binary black

hole simulations. Marronetti et al. (2007) advocate evolving the variable W ≡ exp(−2φ): not only is W regular

everywhere, varying linearly with radius near black hole punctures, but it enters other ﬁeld equations only as W

Hence even if numerical errors drive W slightly negative this will not cause other ﬁeld variables to change sign and

cause codes to crash.

580 Chapter 17 Binary black hole–neutron stars

∂

Q − ∂

(Qβ

) + Q∂

and then adopt the same high-resolution, conservative scheme

to evolving the ﬁeld equations as they use for the hydrodynamic equations. They sur-

mise that this technique proves important because, like many of the other ﬁeld variables,

the term β

∂

Q varies sharply near the puncture. As in other puncture calculations, they

choose an advective “1+log” time slicing condition for the lapse,

∂

ln α = β

∂

ln α − 2K. (17.27)

Their shift condition is a modiﬁed parabolic “Gamma-driver” condition,

∂

= 0.75 ¯γ

+ t∂

), (17.28)

where ¯γ

is the inverse conformal 3-metric and F

≡ δ

∂

¯γ

.Heret is the time step in

the simulation and the second term on the right-hand side of equation (17.28) is employed

to stablize the integration.

Exercise 17.3 Discuss the role of the advective term in equation (17.27).

Hint: ∂

punct

=−β

punct

Exercise 17.4 Recast equation (17.28) in terms of the conformal connection func-

tion



=−∂

¯γ

and compare with the usual Gamma-driver condition (4.82).

In their simulations, Shibata and Ury

u (2006, 2007) adopt equatorial symmetry and a

nonuniform cell-centered Cartesian grid (x, y, z) with a total grid size (2N, 2N, N ). The

inner grid domain has a size (2N

, 2N

, N

) and is uniform, while the outer domain is

nonuniform with gradually increasing grid separation. To test convergence they vary the

resolution, choosing N = 160 − 220, N

= 105 − 150, with a grid spacing in the inner

domain of size x/

M = 1/8 − 7/120, where M ≈ M

irr

is the puncture mass parameter.

The outer boundary falls at L/λ = 0.46–0.83, where λ is the wavelength of the initial

gravitational waveform (λ/M ≈ 50, where M ≈ 5 is the total ADM mass).

They study three cases for low-mass mergers (q

∼

3) in which the initial black hole

irreducible masses are in the range M

= 3.2–4.0M



and the neutron stars at inﬁnite

separation have ADM masses M

= 1.3M



and radii R = 13–14 km, corresponding

to compactions M

= 0.14–0.15. The total ADM masses of the systems are M =

4.5–5.3M



and the total angular momenta are J/M

= 0.65–0.73, corresponding to close,

circular orbits with periods P/M = 110–120.

In all the cases studied, the neutron star is tidally disrupted near the ISCO. Most of the

matter (80–90%) is swallowed by the black hole, with the remainder going into a disk. The

ﬁnal state is a rotating black hole of spin J

≈ 0.4–0.6 surrounded by a disk of mass

∼0.1–0.3M



. An appreciable fraction of the initial angular momentum of the system is

deposited in the disk. As we will discuss below, these disk masses are unrealistically large,

in part because of the assumption of corotation and in part because of the (nonadaptive)

grid structure used in the calculation. Nevertheless, they strengthen the argument that,

since a rotating black hole with an ambient disk could serve as the central engine for a