Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

16.3 Fully relativistic simulations 561

magnetic ﬁeld proﬁle. Such a ﬁeld is small enough to be dynamically unimportant initially,

but large enough to reveal any effects of a ﬁeld once the stars merge. For low-mass cases

in which the remnant is a hypermassive neutron star, Liu et al. (2008) ﬁnd small, but

measurable differences in both the amplitude and phase of the gravitational waveforms

following the merger when compared to the unmagnetized cases. For these cases they again

ﬁnd no appreciable disk. For high-mass cases in which the remnant is a rotating black hole,

they ﬁnd that the hole is surrounded by a disk, and that the disk mass and the gravitational

waveforms are about the same as in the corresponding unmagnetized cases.

The simulation of a magnetized, unequal-mass binary with a total rest mass equal to

1.76 times the Oppenheimer–Volkoff limit is shown in Figure 16.14. The merger leads to

prompt collapse to a black hole surrounded by a disk containing about 2% of the initial

rest mass at the end of the simulation, as in the unmagnetized case.

A comparison of gravitational waveforms is plotted in Figure 16.15 for the merger of

binaries with three different pairs of neutron star companions. Each binary is evolved

both with and without interior magnetic ﬁelds. The quantities plotted are the l = 2, m =

2, s =−2 spin-weighted spherical harmonics of the Weyl tensor ψ

, which may be related

to the wave amplitudes h

and h

using equations (9.126) and (9.133). In particular,

Re (ψ

) =

. The upper panel corresponds to a merger leading to a hypermassive

remnant. The difference in waveforms between the magnetized and unmagnetized mergers

is more pronounced for this case than for the other two, which involve prompt collapse

to black holes. The simulation involving a hypermassive remnant was terminated after the

remnant reached a quasistationary state, but before “delayed collapse” occurs.

Following binary merger and relaxation to a quasistationary state, the magnetic ﬁeld in

a hypermassive remnant can grow substantially by winding and instabilities like MRI. As

a consequence, magnetic ﬁelds can drastically affect the long-term, secular evolution of a

hypermassive remnant. As demonstrated in Chapter 14.2.5, such magnetic ﬁeld ampliﬁ-

cation and turbulence can trigger delayed collapse to a black hole and subsequently drive

gas accretion from the ambient disk onto the hole. The preliminary simulations summa-

rized here suggest that, for coalescing binary neutron stars with astrophysically realistic

magnetic ﬁeld strengths, it is during this secular evolution phase in hypermassive remants

that magnetic ﬁelds may play their most important role.

Binary black hole–neutron

stars: initial data and

evolution

Binary black hole–neutron stars have received signiﬁcantly less attention than binary

black holes or binary neutron stars. No black hole–neutron star binary has been identiﬁed

to date. However, stellar population synthesis models suggest that such systems represent

a signiﬁcant fraction of all compact binary mergers ultimately visible in gravitational

waves by the LIGO detector.

In addition, the study of black hole–neutron star mergers is

important in light of the localizations of short-hard gamma-ray bursts.

These GRB sources

are found in galactic regions of low star-formation devoid of supernovae associations,

ruling out massive stars as progenitors: massive stars have very short lifetimes and would

need to be replenished more rapidly than is possible in low star-formation regions to

account for these bursts. A more plausible progenitor for a short-hard GRB is a compact

binary containing a neutron star, i.e., either a binary neutron star or binary black hole-

neutron star.

The short-hard burst time scales and energetics are consistent with GRB

models based on the coalescence of such compact binaries, and the evolution time scale

of over 1 Gyr between formation and merger is consistent with the low star-formation

rate.

Black hole-neutron star binaries can merge in two distinct ways. The neutron star may

either be tidally disrupted by the black hole companion before being consumed, or it may

be swallowed by the black hole more or less intact. Which one of these two scenarios is

realized depends on whether the tidal disruption occurs sufﬁciently far outside the ISCO,

which, in turn, depends largely on the binary mass ratio

q ≡ M

and the neutron

star compaction

C ≡ M

. To understand the qualitative dependence we can invoke

a very simple Newtonian argument. Consider a particle of mass m on the surface of the

neutron star. The inward gravitational force F

grav

exerted by the neutron star on this mass

grav

. (17.1)

Kalogera et al. (2007).

See, e.g., Berger (2006) and references therein for the physical parameters measured or inferred from Swift and HETE-2

gamma-ray satellite observations.

Paczynski (1986); Narayan et al. (1992).

Belczynski et al. (2002); but note that other GRB models have been proposed.

Note that some authors deﬁne the mass ratio q as the inverse of our convention.

562

Chapter 17 Binary black hole–neutron stars 563

The outward tidal force on m caused by the presence of the black hole companion is

approximately

tid

≈

, (17.2)

where r is the binary separation. We can now estimate the tidal separation r

tid

at which the

star is tidally disrupted by equating these two forces, which yields

tid

 q

−2/3

 q

−2/3

−1

. (17.3)

For a sufﬁciently massive black hole (and thus large q) r

tid

is smaller than the ISCO of

the black hole, so that the neutron star plunges through the ISCO without being disrupted.

For a typical neutron star of compaction

C ≈ 0.15, the critical mass ratio at which tidal

disruption occurs at the ISCO is q

crit

≈ 4 (see equation 17.20 below).

Exercise 17.1 (a) Consider a binary black hole–white dwarf. Use equation (17.3)to

estimate the critical mass of the black hole above which a typical white dwarf can be

swallowed by the hole without disruption. Take M

= M



and R

= 10

−2



(b) Repeat the above calculation for a binary consisting of a black hole and a main

sequence star like the Sun.

Neutron stars with stellar-mass black hole companions are likely to be formed through

normal stellar binary evolution at a rate that depends on the distribution of binary mass

ratios, common-envelope dynamics, the magnitude of imparted supernovae kicks, and

other effects, many of which remain uncertain.

For sufﬁciently tight binaries, merger will

occur within a Hubble time and the orbit will circularize by the time the binary enters

the LIGO gravitational wave detector band. As we can see from the estimate (17.3), the

neutron star will be tidally disrupted before being swallowed if the black hole mass is

sufﬁciently small.

Binaries consisting of neutron stars orbiting very massive black holes form quite differ-

ently from those orbiting stellar-mass black holes. As we have already noted, there is strong

evidence from astrometric observations that massive, compact, “dark” objects reside in

the cores of every bulge galaxy, including the Milky Way. These objects are believed to

be supermassive black holes with masses in the range 10

–10



. Such objects are also

believed to be the engines that power quasars and active galactic nuclei.

Conservative,

N -body gravitational encounters (small-angle, Coulomb scattering) between stars in the

dense cores of galaxies can inject stars, including neutron stars and stellar-mass black

holes, into orbits that move close to the central supermassive black hole. If they pass

sufﬁciently close, these stars may be captured by the hole and subsequently spiral inward

due to the emission of gravitational waves.

The estimate (17.3) shows that neutron stars

See, e.g., Kalogera et al. (2007) and references therein for a discussion.

Rees (1998).

Shapiro (1985); Sigurdsson (2003); Merritt and Poon (2004); Hopman and Alexander (2005).

564 Chapter 17 Binary black hole–neutron stars

captured in this way will be consumed by supermassive black holes before undergoing

tidal disruption. In fact, the internal structure of the neutron star has very little effect on

the orbital evolution of these extreme-mass-ratio inspiral binaries (“EMRIs”). They are,

however, subject to a host of relativistic effects, including periastron and Lense–Thirring

precession, and these strong-ﬁeld effects will leave an imprint on the gravitational wave

signals. For central black holes in the mass range 10

∼

M/M



∼

the emitted waves

will peak in the low frequency band near ∼ 10

−3

Hz, close to the lower limit anticipated

for the LISA gravitational wave interferometer.

Rough estimates suggest that LISA might

be able to detect EMRIs out to a redshift z ∼ 1 and that as many as 10

EMRIs might be

observed during its lifetime. The measured waveforms will be able to chart the spacetime

of the black hole, trace its multipolar structure and conﬁrm that it obeys the Kerr solution.

The orbital dynamics and the expected gravitational waveforms of EMRIs can be treated

by black hole perturbation techniques in the stationary Kerr ﬁeld of the central hole.

However, in this chapter we shall be primarily interested in tight stellar-mass BH-NS

binaries. These systems ultimately inspiral in quasistationary, nearly circular orbits as

the neutron stars approach the horizon. The neutron stars are subject to appreciable tidal

distortion and, in some cases, disruption prior to merger. The strong-ﬁeld spacetime is

dynamical, nonstationary and nonperturbative. For these systems the full machinery of

numerical relativity is necessary to follow the evolution.

As in the case of a binary neutron star merger, a black hole-neutron merger, if observed,

could potentially provide insight into the physics of matter at nuclear densities. For exam-

ple, the onset of mass transfer from the neutron star to the black hole depends on the

neutron star radius, given the stellar masses. The stability and nature of the mass transfer

provides information about the stiffness of the EOS.

Whereas for binary neutron stars the

characteristic frequencies of gravitational wave emission during the merger and formation

of a remnant (either a black hole or hypermassive neutron star) fall beyond the peak sen-

sitivity of an advanced LIGO detector (100–500 Hz), the characteristic frequencies of the

onset of neutron star mass transfer and tidal disruption occur at a lower values, closer to

LIGO’s most sensitive band. Should a gravitational wave signal from a merger be observed

in coincidence with a short-duration GRB, one can determine its distance, luminosity and

characteristic beaming angle.

Black hole–neutron star merger calculations have in common with binary neutron star

calculations the challenge of solving relativistic hydrodynamics in a strong, dynamical,

gravitational ﬁeld. They have in common with binary black hole calculations the additional

complications associated with the presence of a spacetime singularity inside the black hole

from the onset of the simulation. The combination of these two effects helps explain why

See Chapter 9.2.2.

Collins and Hughes (2004).

See, e.g., Babak et al. (2007) and references therein.

Faber et al. (2006a).

See Kobayashi and M

esz

aros (2003) for a discussion.

17.1 Initial data 565

progress on simulating black hole–neutron star mergers has come later than the progress

achieved on the other two problems. But the situation is advancing rapidly, as the techniques

that proved successful in simulating binary neutron stars and black hole binaries have been

adapted successfully to handle black hole–neutron star binaries.

17.1 Initial data

As we found for the other binary systems considered in this book, constructing initial

data serves two independent purposes. Clearly, we need such solutions as initial data for

dynamical simulations, as discussed in Section 17.2 below. In addition we can construct

sequences of constant mass, parametrized by the binary separation, to mimic evolutionary

sequences, and to locate the ISCO or the onset of tidal disruption. The approximate scaling

of the tidal separation r

tid

with the mass ratio and the neutron star compaction is given by

(17.3), but clearly a fully relativistic calculation is required to obtain a more reliable result.

Constructing initial data that model black hole–neutron star binaries basically requires

three ingredients: a solution for the gravitational ﬁelds, a solution for the relativistic

ﬂuid proﬁles inside the neutron star, and a suitable description of the black hole. Fortu-

nately, we can assemble these ingredients from previous sections in this book: we have

developed decompositions of Einstein’s initial value equations in Chapter 3, derived the

equations governing relativistic, stationary ﬂuid solutions in Chapter 15, and modeled

binaries containing black holes in Chapter 12. As in the case of binary black hole initial

data, black hole–neutron star initial data have also been constructed using both the con-

formal transverse-traceless decomposition of Einstein’s constraint equations (Chapter 3.2)

and the conformal thin-sandwich decomposition (Chapter 3.3). We shall begin with the

latter approach in Section 17.1.1, and will then brieﬂy review the former in Section 17.1.2.

17.1.1 The conformal thin-sandwich approach

A systematic study of quasiequilibrium, black hole–neutron star binary initial data has

been carried out by the group at the University of Illinois.

Their hierarchical treatment,

which is based on the conformal thin-sandwich approach, started with several simplifying

assumptions, including extreme mass ratios and corotating neutron stars, and then relaxed

these assumptions one at a time. Here we will focus on their models of irrotational bina-

ries, by which we mean irrotational neutron stars orbiting nonspinning black holes, with

companions of comparable mass. They have also generated initial data by this method

to describe binaries of comparable mass containing irrotational neutron stars and spin-

ning black holes. They have used these initial data sets to evolve representative binary

conﬁgurations,

and these simulations will be discussed in Section 17.2.2.

Baumgarte et al. (2004); Taniguchi et al. (2005, 2006, 2007, 2008); see also Grandcl

ement (2006) for a similar

approach.

See, e.g., Etienne et al. (2008, 2009) and references to earlier work.

566 Chapter 17 Binary black hole–neutron stars

The gravitational ﬁeld equations

In Chapter 3.3 we introduced the conformal thin-sandwich decomposition of Einstein’s

constraint equations and saw how it is well suited for the construction of equilibrium

initial data (see Box 3.3 for a summary). To describe an equilibrium binary we assume the

existence of an approximate, helical Killing vector. In a corotating coordinate system we

may then set to zero the time derivative of both the conformally related metric and the mean

curvature, i.e.,

= ∂

¯γ

= 0and∂

K = 0. If we further adopt maximal slicing K = 0

and conformal ﬂatness ¯γ

= η

, the equations reduce to the Hamiltonian constraint

ψ =−

−7

− 2πψ

ρ, (17.4)

the momentum constraint

(



β)

= 2

(αψ

−6

) + 16παψ

, (17.5)

and the condition ∂

K = 0, which, from equation (2.137), yields

(αψ) = αψ



−8

+ 2πψ

(ρ + 2S)



. (17.6)

Here

=∇

is the ﬂat Laplace operator,



the ﬂat vector Laplacian deﬁned in equa-

tion (3.51),

and

is given by

2α

(

Lβ)

, (17.7)

where the vector gradient

L is deﬁned in equation (3.50). For given matter sources and

boundary conditions these equations can be solved as in Chapters 12 and 15.

Relativistic equations of stationary equilibrium

We can determine the matter sources appearing in equations (17.4)–(17.6) by solving

the relativistic hydrodynamic equations in stationary equilibrium, which we derived in

Chapter 15. In particular, we need to ﬁnd stationary solutions of the Euler equation (15.34)

and the continuity equation (5.7).

For a corotational star, which is static as viewed in a corotating coordinate system, the

continuity equation is satisﬁed identically, and the Euler equation can be integrated once

to yield the algebraic equation (15.46),

= C. (17.8)

Here h is the ﬂuid’s enthalpy, u

is the time-component of the ﬂuid’s 4-velocity, and

C is a constant of integration that has to be determined as part of the iteration. Using

See exercise 3.8 for an example.

17.1 Initial data 567

the normalization of the 4-velocity u

=−1, we can express u

in terms of its spatial

components (see equation 15.47) and, hence, in terms of the binary’s orbital angular velocity

. The solution for h, which can expressed in terms of the matter source proﬁles once we

specify an equation of state, depends on the gravitational ﬁelds through this normalization

condition. The ﬁeld and ﬂuid equations therefore have to be solved simultaneously, as

outlined in Chapter 15.2.

For more realistic irrotational stars,

we can express the 4-velocity in terms of a gradient

of a velocity potential  as in equation (15.65),

=∇

. (17.9)

Deﬁning B

as the shift vector in the corotating coordinate system (15.70), we can again

integrate the Euler equation to ﬁnd an algebraic equation for the enthalpy h

(C + B

)

− D

D

, (17.10)

where C is again a constant of integration (see equation 15.76). The continuity equation,

however, is no longer satisﬁed identically, and now results in an elliptic equation for the

velocity potential ,

 − D



C + B







C + B



− D





αρ

(17.11)

(see equation 15.78). As in the case of corotational stars, these ﬂuid equations have to

be solved simultaneously with the constraint equations (17.4)–(17.6). Before we can do

that, though, we have to impose appropriate boundary conditions on the gravitational ﬁeld

variables.

Quasi-equilibrium black hole boundary conditions

Assuming asymptotic ﬂatness, we may impose the asymptotic fall-off conditions (12.73)

at inﬁnity, or at a large separation from the binary. To avoid the black hole singularity, we

excise the black hole interior, usually taken to be a coordinate sphere, and impose black

hole equilibrium boundary conditions on the surface of this excised region. We derived

these boundary conditions in Chapter 12.3.1 from the notions of apparent and isolated

horizons (see Chapters 7.3 and 7.4).

To formulate these boundary conditions it proved convenient to split the shift vector

into parts that are normal and tangential to the excision surface, β

⊥

and β



(see

equation 12.82). The normal component must then satisfy condition (12.84)

⊥

= α, (17.12)

See Faber et al. (2006a), who show why binary black hole-neutron stars are likely to be irrotational, or footnote 27 for

a brief summary.

568 Chapter 17 Binary black hole–neutron stars

while the tangential components β



must form a conformal Killing vector of the the induced

metric on the excision surface (see equation 12.106), which can be constructed from



= 

spin

(17.13)

(see equation 12.107). Here ξ

= 

ijk

is the Killing vector of a unit sphere, where

is a unit vector aligned with the axis of rotation,

the unit normal on the sphere’s

surface, and 

spin

is a yet undetermined parameter associated with the black hole’s spin.

We furthermore found that the conformal factor ψ has to satisfy the Neumann boundary

condition (12.90), while the lapse α can be chosen arbitrarily.

We can now construct an iterative algorithm to solve the above equations self-

consistently. In Chapter 15.2 we outlined such an algorithm for an equal-mass, corotating

neutron star binary, and we have discussed the construction of irrotational binaries in

Chapter 15.3. Here the situation is more complicated, because we have replaced one of the

two neutron stars with a black hole, and we can no longer assume the two masses to be

equal. Allowing for these differences therefore entails several additional nested iterations.

One of these new iterations adjusts the location of the binary’s axis of rotation – assumed to

intersect the coordinate axis connecting the centers of the black hole and the neutron star –

until the binary’s total linear momentum vanishes. Another iteration adjusts the coordinate

radius of the excised sphere until the black hole’s irreducible mass (7.2) equals its desired

value. This still leaves undetermined the spin parameter 

spin

in the boundary condition

(17.13). A corotating black hole would be nonspinning in a corotating coordinate system,

which corresponds to 

spin

= 0. More interesting are nonspinning black holes. We might

attempt to construct such binaries by setting 

spin

equal to the orbital angular speed, which

we called the “leading-order spin approximation” in Chapter 12.4. As we discussed there,

however, it is more accurate to iterate over 

spin

until the black hole’s quasi-local spin

(7.74) vanishes. To treat spinning black holes, we iterate over 

spin

until the black hole

spin equals the desired value.

Numerical results

Taniguchi et al. (2008) solve the above equations with the spectral methods of the

LORENE

package to construct irrotational black hole–neutron star binaries. As we

discussed in the context of binary neutron stars in Chapter 15.3, it is again useful to split

all gravitational ﬁeld variables into parts that are associated with one or the other com-

panion star (see equation 15.81). The resulting two equations can then be solved on two

separate computational domains, one centered on the black hole, and one on the neutron

star. Only the equation associated with the black hole needs to be excised, if all source

terms affected by those excised quantities are moved into the black hole equation.

See http://www.lorene/obspm.fr/.

See the discussion following equation (15.81); also see Appendix A in Taniguchi et al. (2007) for a detailed treatment.

17.1 Initial data 569

X / M

Y / M

−5

Figure 17.1 Contours of the conformal factor ψ in the orbital plane for an irrotational binary black

hole–neutron star close to tidal break-up. This binary has a mass ratio of q = 3, and the neutron star, governed by

a polytropic equation of state with polytropic index n = 1, has a compaction of M

= 0.1452, where M

the ADM mass that the star would have in isolation and R

its areal radius. The circle on the left marks the black

hole’s apparent horizon. The interior of this coordinate circle is excised from the computational grid. The other

thick line on the right marks the neutron star’s deformed surface. The cross “×” indicates the position of the

rotation axis. [From Taniguchi et al. (2008).]

Taniguchi et al. (2008) adopt a polytropic equation of state (5.18) with  = 2 (i.e., poly-

tropic index n = 1) to describe the neutron star matter. They consider mass ratios

1 ≤ q ≤ 10, where q ≡ M

is the ratio of the irreducible mass of the black hole to

the ADM mass of a spherical, isolated neutron star. The neutron stars in isolation would

have a compaction in the range 0.1088 ≤ M

≤ 0.1780, where R

is the areal radius.

The most compact neutron star model has a rest mass that corresponds to 94% of the

maximum allowed rest mass for a nonrotating,  = 2 polytrope in isolation. A typical

conﬁguration, close to the formation of a cusp in the neutron star’s surface that marks the

onset of tidal disruption,

isshowninFigure17.1.

We can mimic inspiral sequences by constructing constant-mass sequences of black

hole-neutron stars, parametrized by the binary separation. In this case, the conserved

masses are the rest mass M

of the neutron star and the irreducible mass M

irr

of the black

hole. For these sequences we can measure the total angular momentum J as well as the

binding energy E

, deﬁned as

≡ M

ADM

− M

. (17.14)

Here M

is the total ADM mass of the system at inﬁnite binary separation, i.e., the sum of

the black hole’s irreducible mass and the neutron star’s ADM mass in isolation,

= M

+ M

. (17.15)

The spectral methods used in these calculations break down when the stellar surface forms a cusp – see our discussion

in Chapter 15.3. The authors therefore introduce a “mass-shedding indicator” χ as in equation (15.82) and use

extrapolation to locate the onset of tidal disruption.

570 Chapter 17 Binary black hole–neutron stars

0.44 0.46 0.48

0.5 0.52

J / M

−0.011

−0.01

−0.009

−0.008

−0.007

−0.006

/ M

= 0.13

= 0.14

= 0.15

= 0.16

= 0.17

3PN approximation

Old results in Paper I

= 0.15

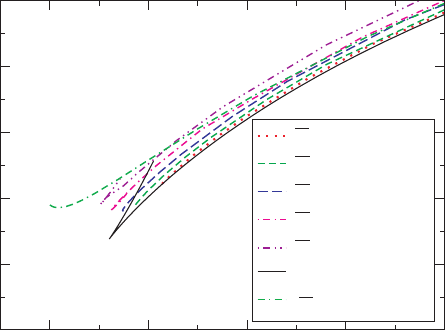
Figure 17.2 Binding energy E

vs. the total angular momentum J for a polytropic n = 1 binary with mass ratio

q = 5. The “old results in Paper I” refer to results obtained with the “leading-order spin approximation” for the

parameter 

spin

in the black hole boundary conditions. The quantity

denotes the dimensionless (baryon)

rest mass of the neutron star and is larger for higher compactions; the maximum isolated mass corresponds to

= 0.18. [From Taniguchi et al. (2008).]

In Figure 17.2 we show the binding energy as a function of angular momentum for

binaries of mass ratio q = 5. The graph includes results for several different neutron star

compactions, the post-Newtonian point-mass result (which is independent of neutron star

compaction; see Appendix E), as well as a “leading-order” spin result that we return to

below. We ﬁrst observe that the numerical results agree with the the post-Newtonian result

to very high precision for low neutron star compactions; for larger compactions, which

imply stronger gravitational ﬁelds, the deviation increases slightly.

A simultaneous turning-point in the binding energy E

and the angular momentum J

marks the onset of an orbital instability; we therefore identify the corresponding orbit

with the ISCO. When we plot E

vs. J , as in Figure 17.2, such a simultaneous turning

point results in a cusp. The post-Newtonian curve, for example, displays such a cusp

very clearly. For the numerical results, however, only those with the larger compaction

feature a cusp. This is because the numerical results terminate just before the onset of

tidal disruption. For small neutron star compactions, the tidal separation is larger than the

ISCO separation, so that the corresponding curves never reach an ISCO. We anticipated

this ﬁnding qualitatively from equation (17.3), which demonstrates that, for a given binary

mass ratio, a smaller compaction

C = M

leads to a larger tidal separation r

tid

.If

The cusp in the E

vs. J curve, identifying an ISCO, should not be confused with the cusp in the stellar surface at the

onset of tidal disruption.