Bhushan B. Handbook of Micro/Nano Tribology, Second Edition

Подождите немного. Документ загружается.

magnetic ﬁlm and 20-nm-thick sputtered hydrogenated, DLC ﬁlm) are compared in Figure 10.49.

Figure 10.49 also includes the friction force proﬁle for a single-crystal silicon substrate for comparison.

SEM images of two regions of 500-µm-long scratches made at 1 to 12 mN normal load on various samples

are compared in Figure 10.50. The upper images in the sets of two images for each sample correspond

to a region where friction increased abruptly. These are the points indicated by “A” in Figure 10.50. The

lower images in each set correspond to the region that is very close to the end of a scratch. These are the

points indicated by ‘B’ in Figure 10.50. The extent of a damage in a scratch is estimated by the width and

depth of the scratch and by the amount of debris generated toward the end of the scratch.

Single-crystal silicon exhibited the lowest friction with little plowing at a low load and cracking at

higher loads. This observation suggests that scratching of silicon took place primarily by brittle defor-

mation. In the case of the Ni–P-coated Al–Mg substrate, friction increase was continuous from the

beginning of the scratching, Figure 10.49. SEM images of the Ni–P-coated Al–Mg substrate presented in

Figure 10.50, show the material removal occurred by plowing with formation of curly ductile chips. It is

evident that scratching took place primarily by plastic deformation typical of ductile materials. Plowing

is responsible for the continuous increase in the friction for this substrate. Glass and glass–ceramic

substrates and corresponding disks and the Ni–P-coated Al–Mg disk exhibited relatively low friction with

a sudden increase at higher load. The glass substrate exhibited the lowest friction followed by the

glass–ceramic substrate. In the case of the Ni–P-coated Al–Mg disk, the load at which friction increased

was lower than that of the glass and glass–ceramic substrates. SEM images of these samples exhibit

plowing in addition to the formation of ﬁne debris. There is no evidence of cracking of ceramic substrates

or the ceramic overcoats used in all disks at magniﬁcations as high as 50,000¥. Glass is chemically

strengthened in order to produce signiﬁcant compressive stresses in the glass surface. Glass–ceramic

consists of ﬁne-grained polycrystalline material in a glass matrix. Chemical strengthening and the crystals

add to the fracture toughness of the material. Thus, both ceramic substrate materials are expected to

deform with ductile and brittle deformation modes. Ductile deformation results in plowing, whereas

brittle deformation aids in debris generation. Lower values of the coefﬁcient of friction before a sudden

increase, as compared with Ni–P-coated Al–Mg substrate, suggest that brittle fracture contributes to

overall deformation. Hard overcoats generally consist of signiﬁcant compressive residual stresses. It is

these compressive stresses that allow ductile deformation with little cracking. We further note that a

sudden increase in the coefﬁcient of friction for ceramic substrates and for all disks at some load results

from signiﬁcant damage to the bulk material or to the coating surface (Figure 10.50).

Based on the friction data, the width and depth of scratches, the amount of debris generated, and

scratch morphology, glass substrates and corresponding disks exhibit a lower coefﬁcient of friction against

a diamond tip and a superior resistance to scratch, followed by glass–ceramic substrates and correspond-

ing disks.

This example clearly suggests that deformation modes and critical load to failure can be identiﬁed

using the scratch technique.

10.6 Nanoindentation and Microscratch Techniques

for Adhesion Measurements, Residual Stresses,

and Materials Characterization of Thin Films

Adhesion describes the sticking together of two materials. Adhesion strength, in a practical sense, is the

stress required to remove a coating from a substrate. Indentation and scratch on the micro- and nanoscales

are the two commonly used techniques to measure adhesion of thin hard ﬁlms with good adhesion to

the substrate (>70 MPa)(Campbell, 1970; Mittal, 1978; Blau and Lawn, 1986; Bhushan, 1987; Bhushan

and Gupta, 1997). Nearly all coatings, by whatever means they are produced, and surface layers of treated

parts are found to be in a state of residual (intrinsic or internal) stress. These are elastic stresses that exist

in the absence of external forces and are produced through the differential action of plastic ﬂow, thermal

contraction, and/or changes in volume created by phase transformation. Microindentation and nanoin-

FIGURE 10.50 SEM images of two regions on 500-µm-long scratches made at 1 to 12 mN load on (a) various ceramic

substrates and corresponding magnetic disks and (b) single-crystal silicon. The scratching direction was from left to

right. The upper images in the sets of two images for each sample correspond to a location or normal load where the

friction increased abruptly and/or damage began to occur. These are the points indicated by “A” in Figure 10.49. The

lower images correspond to a location close to the end of the scratch (~11 mN). These are the points indicated by “B”

in Figure 10.49. (From Bhushan, B. and Gupta, B.K., 1995, Adv. Info. Storage Syst. 6, 193–208. With permission.)

dentation techniques are also used to measure residual stresses (Bhushan and Gupta, 1997). Microscratch

and nanoscratch techniques (using nanoindenter) are also used to measure scratch resistance of surfaces

of bulk materials (Bhushan and Gupta, 1995; Bhushan et al., 1996). The nanoindenter has also been

modiﬁed to conduct microwear studies (Wu and Lee, 1994).

In this section, we describe adhesion measurements, residual stress measurements, and microwear

measurements using nanoindentation and microscratch apparatuses. We also present typical examples.

10.6.1 Adhesion Strength and Durability Measurements

Using Nanoindentation

In the indentation test method, the coating sample is indented at various loads. At low loads, the coating

deforms with the substrate. However, if the load is sufﬁciently high, a lateral crack is initiated and

propagated along the coating–substrate interface. The lateral crack length increases with the indention

load. The minimum load at which the coating fracture is observed is called the critical load and is

employed as the measure of coating adhesion (Figure 10.51). For relatively thick ﬁlms, the indentation

is generally made using a Brinell hardness tester with a diamond sphere of 20-µm radius (Tangena and

Hurkx, 1986), Rockwell hardness tester with a Rockwell C 120° cone with a tip radius of 200 µm (Mehrotra

and Quinto, 1985) or a Vickers pyramidal indenter (Chiang et al., 1981; Lin et al., 1990; Alba et al., 1993).

However, for extremely thin ﬁlms, a Berkovich indenter (Stone et al., 1988) or a conical diamond indenter

with a tip radius of 5 mm and 30° of included angle (Tsukamoto et al., 1992) is used in a nanoindenter.

It should be noted that the measured critical load W

is a function of hardness and fracture toughness

in addition to the adhesion of coatings. Chiang et al. (1981) have related the measured crack length

during indentation, the applied load, and the critical load (at which coating fracture is observed) to the

fracture toughness of the substrate–coating interface. A semianalytical relationship derived between the

measured crack length c and the applied load W:

(10.23)

where

is a numerical constant, t

is the coating thickness, H is the mean hardness, and (K

)

interface

is the

fracture toughness of the substrate–coating interface. Mehrotra and Quinto (1985) used this analysis to

calculate fracture toughness of the interface.

FIGURE 10.51 Schematic illustration of the indentation method for adhesion measurement.

W=−













α 1

32 12

()

interface

Marshall and Oliver (1987) estimated adhesion of composites by measuring the magnitude of shear

(friction) stresses at ﬁber/matrix interfaces in composites. They used a Berkovich indenter to push on

the end of an individual ﬁber, and measured the resulting displacement of the surface of the ﬁber below

the matrix surface (due to sliding). The shear stress was calculated from the force–displacement relation

obtained by analysis of the frictional sliding. The force and displacement measurements were obtained

only at the peak of the load cycle, and the sliding analysis was based on sliding at constant shear resistance

at the interface. These experiments provided measurements of average shear stresses at individual ﬁbers.

10.6.2 Adhesion Strength and Durability Measurements

Using Microscratch Technique

Scratching the surface with a ﬁngernail or a knife is probably one of the oldest methods for determining

the adhesion of paints and other coatings. In 1822, Friedrich Mohs used resistance to scratch as a measure

of hardness. Scratch tests to measure adhesion of ﬁlms was ﬁrst introduced by Heavens in 1950 (Heavens,

1950). A smoothly round chrome-steel stylus with a tungsten carbide or Rockwell C diamond tip (in the

form of 120° cone with a hemispherical tip of 200-mm radius) (Perry, 1981, 1983; Mehrotra and Quinto,

1985; Valli, 1986; Steinmann et al., 1987) or Vickers pyramidal indenter (Burnett and Rickerby, 1987a;

Bull and Rickerby, 1990) for macro- and microscratching a conical diamond indenter (with 1 or 5 µm

of tip radius and 60° of included angle) for nanoscratching (Wu et al., 1989, 1990b; Wu, 1991) is drawn

across the coating surface. A normal load is applied to the scratch tip and is gradually increased during

scratching until the coating is completely removed. The minimum or critical load at which the coating

is detached or completely removed is used as a measure of adhesion (Benjamin and Weaver, 1960;

Campbell, 1970; Greene et al., 1974; Ahn et al., 1978; Mittal, 1978; Perry, 1981, 1983; Laugier, 1981;

Jacobson et al., 1983; Mehrotra and Quinto, 1985; Je et al., 1986; Valli, 1986; Burnett and Rickerby, 1987a;

Steinmann et al., 1987; Sekler et al., 1988; Wu et al., 1989, 1990b; Wu, 1990, 1991; Bull and Rickerby,

1990; Cheng et al., 1990; Julia-Schmutz and Hintermann, 1991; White et al., 1993; Bhushan et al., 1995,

1998; Gupta and Bhushan, 1995a,b; Patton and Bhushan, 1996; Bhushan and Patton, 1996; Bhushan and

Li, 1997; Li and Bhushan, 1998b,c). It is a most commonly used technique to measure adhesion of hard

coatings with strong interfacial adhesion (>70 MPa).

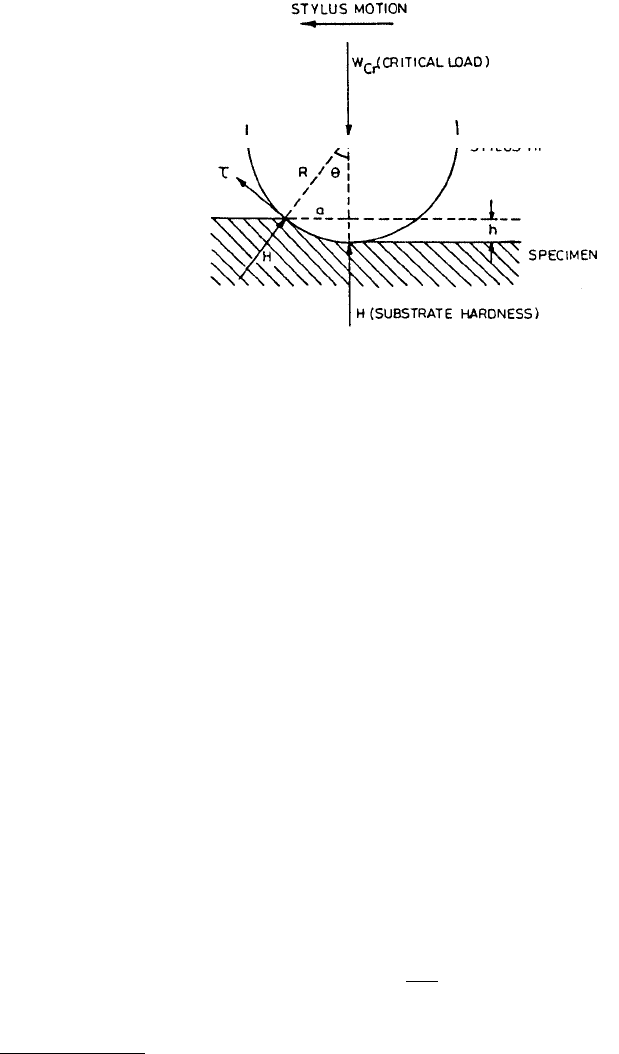
For a scratch geometry shown in Figure 10.52, surface hardness H is given by

(10.24)

FIGURE 10.52 Geometry of the scratch.

and adhesion strength t is given by (Benjamin and Weaver, 1960)

(10.25a)

(10.25b)

where W

is the critical normal load, a is the contact radius, and R is the stylus radius.

Burnett and Rickerby (1987a) and Bull and Rickerby (1990) analyzed the scratch test of a coated

sample in terms of three contributions: (1) a plowing contribution which will depend on the indentation

stress ﬁeld and the effective ﬂow stress in the surface region, (2) an adhesive friction contribution due

to interactions at the indenter–sample interface, and (3) an internal stress contribution since any internal

stress will oppose the passage of the indenter through the surface, thereby effectively modifying the

surface ﬂow stress. They derived a relationship between the critical normal load W

and the work of

adhesion W

(10.26)

where E is the Young’s modulus of elasticity and t is the coating thickness. Plotting of W

as a function

of a

1/2

should give a straight line of the slope π(2EW

/t)

1/2

/2 from which W

can be calculated. Bull

and Rickerby suggested that either the line slope (interface toughness) or W

could be used as a measure

of adhesion.

An accurate determination of critical load W

sometimes is difﬁcult. Several techniques, such as (1)

microscopic observation (optical or SEM) during the test, (2) chemical analysis of the bottom of the

scratch channel (with electron microprobes), and (3) acoustic emission, have been used to obtain the

critical load (Perry, 1981, 1983; Je et al., 1986; Valli, 1986; Steinmann et al., 1987; Sekler et al., 1988; Wu

et al., 1990b; Wu, 1991). In some instruments, tangential (or friction) force is measured during scratching

to obtain the critical load (Jacobson et al., 1983; Valli, 1986; Wu et al., 1990b; Wu, 1990, 1991; Anonymous,

1991; Bhushan et al., 1995, 1997; Gupta and Bhushan, 1995a,b; Patton and Bhushan, 1996; Bhushan and

Patton, 1996; Bhushan and Li, 1997; Li et al., 1998b,c). The AE and friction force techniques have been

reported to be very sensitive in determining critical load. AE and friction force start to increase as soon

as cracks begin to form perpendicular to the direction of the moving stylus.

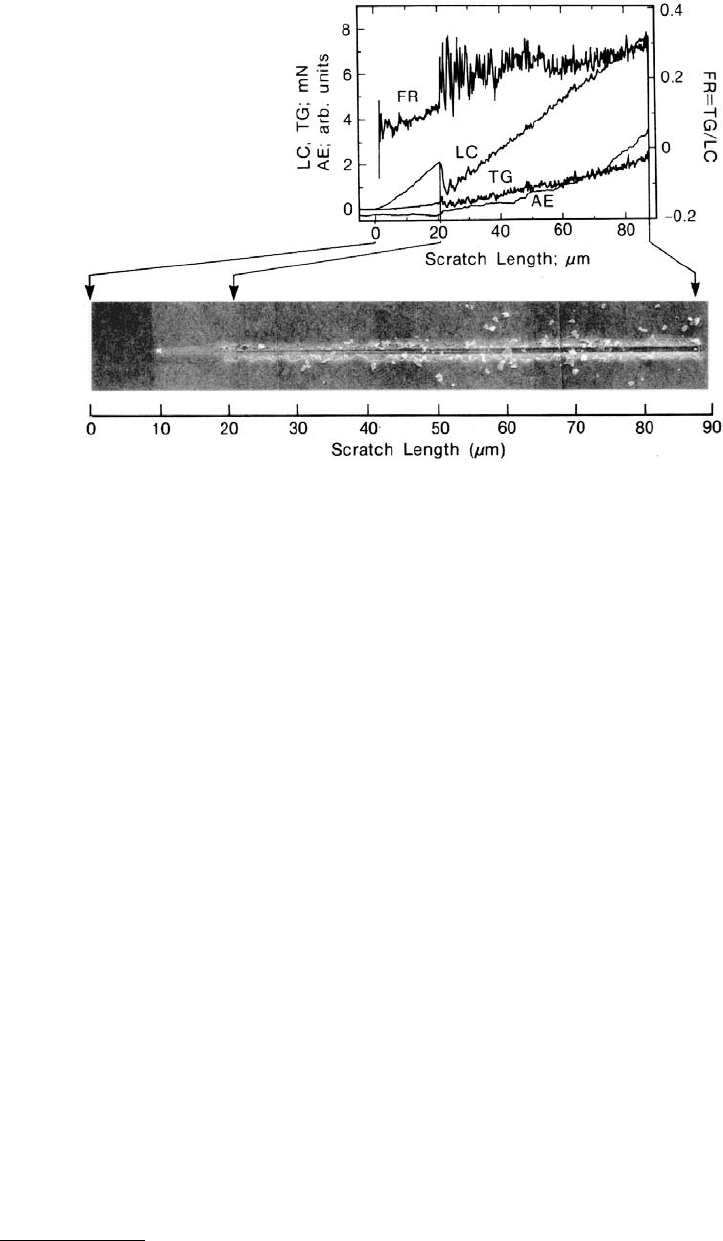
Wu (1991) has used the scratch technique to study the adhesion and scratch resistance of diamondlike

carbon and zirconia coatings deposited on Si(100) substrates. Figure 10.53 shows the scratch morphology

at increasing normal loads and typical scratch data (normal load, tangential load and acoustic emission

as well as calculated apparent coefﬁcient of friction). We note that all three monitored outputs (LC, TG

and AE) detected the ﬁrst spallation event of the carbon coating by showing sudden changes in their

output signals.

Bhushan et al. (1995, 1997), Bhushan and Li (1997), Gupta and Bhushan (1995a,b), Patton and

Bhushan (1996), and Li and Bhushan (1998b,c) have used the scratch technique to study adhesion and

scratch resistance (mechanical durability) of various ceramic ﬁlms. Scratch tests conducted with a sharp

diamond tip simulate a sharp asperity contact. Bhushan et al. have also conducted accelerated friction

τθ=

−

()













tan

τ=

if 













and wear (ball-on-coated disk) and functional tests and have found a good correlation between the

scratch resistance and wear resistance measured using accelerated tests (Bhushan et al., 1995a, 1997;

Gupta and Bhushan, 1995b; Patton and Bhushan, 1996; Bhushan and Patton, 1996; Bhushan and Li,

1997; Li and Bhushan, 1998b,c) and functional tests (Patton and Bhushan, 1996; Bhushan and Patton,

1996; Bhushan et al., 1997). Based on this work, scratch tests can be successfully used to screen materials

and coatings for wear applications.

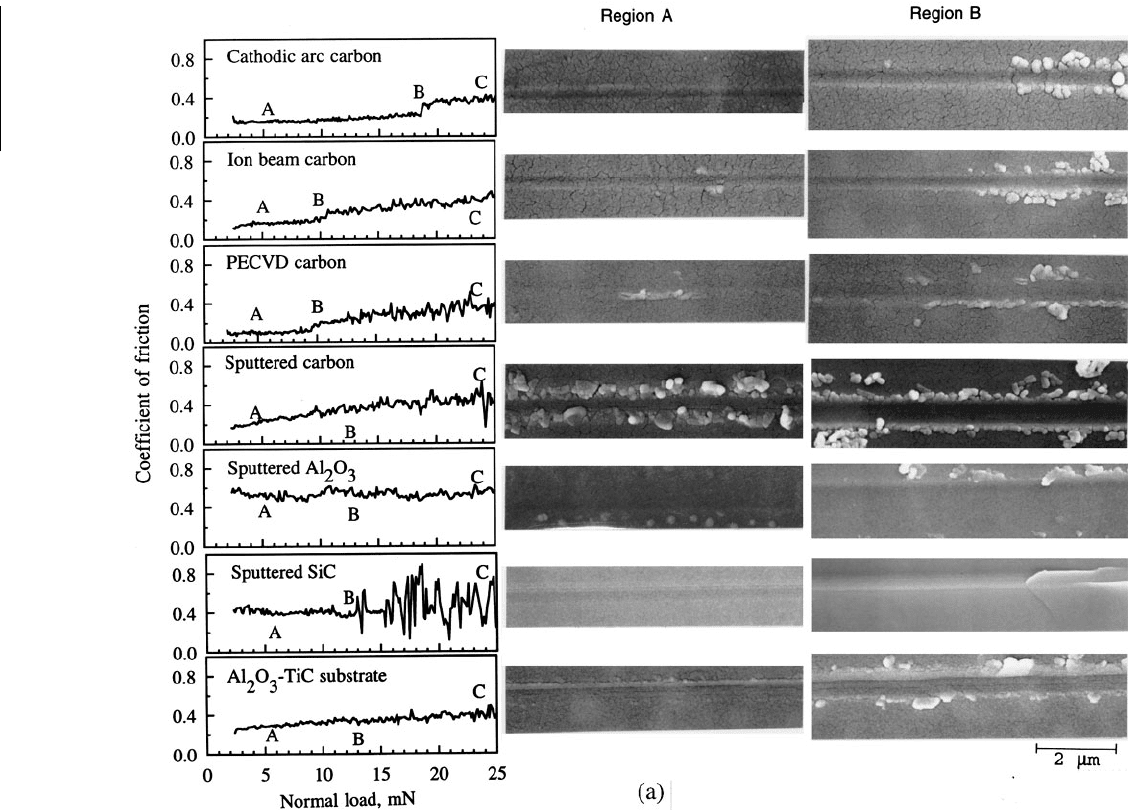
Gupta and Bhushan (1995b) conducted scratch tests on 20-nm-thick DLC ﬁlms deposited by several

deposition techniques and sputtered Al

and sputtered SiC ﬁlms on Al

–TiC (70–30 wt%) substrate.

Films were scratched using a 1-µm-radius conical tip at ramping loads ranging from 2 to 25 mN with a

scratch length of 500 µm. The friction proﬁles as a function of increasing normal load and SEM images

of three regions over scratches — at the beginning of the scratch (indicated by A on friction proﬁle), at

the point of initiation of damage at which coefﬁcient of friction increases abruptly to a very high value

(indicated by B on friction proﬁle), and toward the end of scratch (indicated by C on friction proﬁle) —

made on various carbon, ion beam-sputtered Al

, and DC-sputtered SiC ﬁlms on Al

–TiC substrates

and uncoated substrate are compared in Figure 10.54. The cathodic arc carbon ﬁlm exhibits a low

coefﬁcient of friction of about 0.20 during scratch and a critical load of about 19 mN. All ﬁlms except

cathodic arc carbon on Al

–TiC substrates exhibit a continuous increase in the coefﬁcient of friction

during scratching and were damaged at much lower normal loads. Cathodic arc carbon ﬁlm exhibited

scratches with a width of about 0.9 µm (at about 22 to 25 mN normal load) comparable to that of ion

beam carbon and sputtered carbon coating but lower than that PECVD carbon coating. A qualitative

comparison of the amount of debris generated during scratching reveals that minimum debris was formed

in the case of cathodic arc carbon coating, Table 10.6. These observations suggest that cathodic arc carbon

coating on Al

–TiC substrate has a superior scratch resistance compared with other coatings. The RF-

sputtered SiC coating on Al

–TiC exhibited lower scratch resistance than that of cathodic arc carbon

coating on Al

–TiC and higher scratch resistance than that of all other carbon coatings, Table 10.6.

FIGURE 10.53 Scratch morphology and typical scratch data of 0.11-µm-thick DC-sputtered DLC ﬁlm on an Si

substrate. The monitored outputs are the normal load (LC), tangential load (TG), acoustic emission (AE). The

apparent coefﬁcient of friction (FR = TG/LC) is also shown. (From Wu, T.W. et al., 1990, in Symp. Proc., Vol. 188,

pp. 207–212, Materials Research Society, Pittsburgh. With permission.)

Accelerated friction tests were conducted by sliding a diamond tip (20-µm radius) and a single-crystal

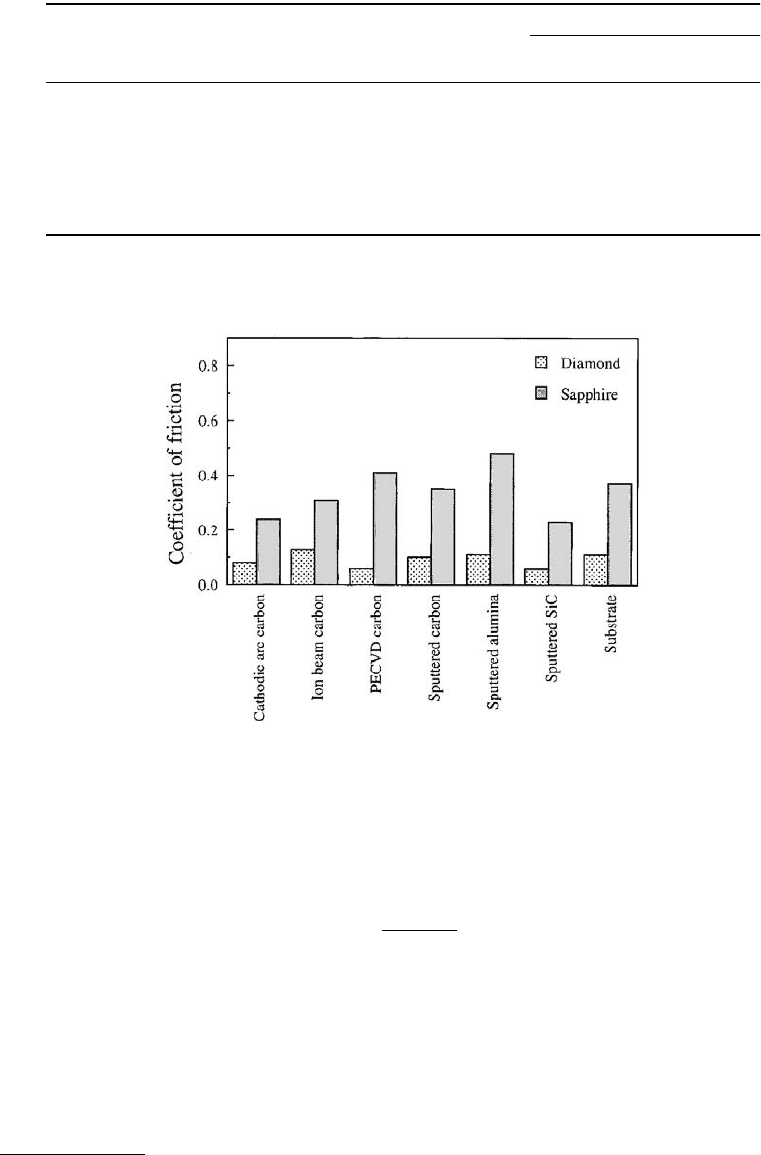
sapphire ball (3-mm diameter) against the ﬁlms. The data are compared in Figure 10.55. We note that

the coefﬁcients of friction of all of the coatings are low (≈0.06 to 0.13) when these were slid against a

diamond tip, whereas these coatings exhibited higher coefﬁcients of friction from 0.20 to 0.50 when slid

against a sapphire ball. SiC coating exhibited the lowest coefﬁcients of friction among other coatings,

when it was slid against a sapphire ball. Based on optical examination of worn samples, there were no

wear tracks formed when cathodic arc carbon, ion beam carbon, PECVD carbon, and SiC coatings were

slid for 2 h against a diamond tip at 10 mN load. Sputtered carbon and sputtered Al

coatings exhibited

a small amount of wear debris, because of their lower scratch resistance. On the other hand, for the

coatings slid for 2 h against a sapphire ball, the cathodic arc carbon and SiC coatings on Al

–TiC

substrate did not form any wear track, Figure 10.56. The higher wear performances of cathodic arc carbon,

ion beam carbon, and SiC coatings are attributed to their high resistance to scratch and high hardnesses

and elastic moduli.

Magnetic thin-ﬁlm head sliders made with Al

–TiC substrate are used in magnetic storage applica-

tions (Bhushan, 1996). Multilayered thin-ﬁlm pole-tip structure present on the head slider surface wears

more rapidly than the Al

–TiC substrate, which is much harder. Pole-tip recession (PTR) is a serious

concern in magnetic storage. Two of the DLC coatings superior in mechanical properties — ion beam

and cathodic arc carbon — were deposited on the air bearing surfaces of Al

–TiC head sliders. The

functional tests were conducted by running a metal-particle (MP) tape in a computer tape drive. Average

PTRs as a function of sliding distance data are presented in Figure 10.57. We note that PTR increases for

the uncoated head, whereas for the coated heads there is a slight increase in PTR in early sliding followed

by little change. Thus, coatings provide protection.

This example clearly suggests that material characterizations (hardness, elastic modulus, and scratch

resistance) are powerful ways of screening materials and the data correlates well with the functional

friction and wear performance.

10.6.3 Residual Stress Measurements Using Nanoindentation

Indentation measurements similar to those used to determine the hardness and elastic modulus of a ﬁlm

can also be used to measure the residual stresses in it. When a compressive force on a biaxially stressed

ﬁlm during indentation is applied in a direction perpendicular to the ﬁlm, yielding will occur at a smaller

applied compressive force while a ﬁlm is stressed in biaxial tension as compared with the unstressed ﬁlm.

Thus, the biaxial tension decreases hardness and the biaxial compression increases hardness (Swain et al.,

1977; Vitovec, 1986). LaFontaine et al. (1990c, 1991) used the nanoindentation technique to measure the

effect of residual stresses on the hardness of thin ﬁlms. For samples that do not undergo large structural

changes, changes in hardness with time reﬂect a change in residual stress in the ﬁlm (LaFontaine et al.,

1990c, 1991). LaFontaine et al. (1991) measured the stress relaxation in thin aluminum ﬁlms and the

residual stresses on identical ﬁlms using an X-ray stress measurement technique. Results of the indenta-

tion and X-ray stress measurements compared closely, implying that decrease in hardness with time

resulted from the relaxation of residual stresses. Thus, the indentation measurements can be used to

investigate stresses in thin ﬁlms. Due to the presence of a stress gradient in thicker (>1 µm) ﬁlms, the

technique is not applicable.

Tsukamoto et al. (1987) measured the deﬂection at the center of the bent beam (bent as a result of

residual stresses in the ﬁlm) by pressing the beam ﬂat with a nanoindenter. The bent beam is placed on

a ﬂat glass surface supported by two fulcrums, and a load–deﬂection curve is generated (Figure 10.58).

The distance h

can be estimated from the inﬂection point in the curve. Because of limited ﬂatness of

most substrates, the ﬁlm is removed from the substrate, and then the initial deﬂection is measured. The

true deﬂection resulting from residual stresses in the ﬁlm equal to h

– h

. The curvature (1/R) of the

substrate can then be calculated by the geometric relationship,

FIGURE 10.54 (a) Coefﬁcient of friction proﬁles as

a function of normal load and SEM images of three

regions over scratches; at the beginning of the scratch

(indicated by A on friction proﬁle), at the point of

initiation of damage at which coefﬁcient of friction

increases abruptly to a very high value (indicated by

B on friction proﬁle) and (b) toward the end of

scratch (indicated by C on friction proﬁle), made on

various DLC, Al

, and SiC ﬁlms on Al

–TiC sub-

strates and uncoated Al

–TiC substrate. (From

Gupta, B.K. and Bhushan, B., 1995, Wear 190,

110–122. With permission.)

(10.27)

where L is the span.

Hong et al. (1990) used another deﬂection measurement technique. In this technique, a circular section

of the substrate is removed from beneath the ﬁlm to produce a drum-headlike membrane and the load

is applied at its center. The stiffness of the membrane (ﬁlm) is a sensitive function of the biaxial tension

in it. The deﬂection h is related to load W as

TABLE 10.6 Coefﬁcient of Friction (at the beginning), Critical Load Estimated from an Abrupt Increase

in Friction during Scratching, and Width of Scratches at about 23–25 mN Normal Load, Measured

from SEM Images, and Qualitative Comparison of the Amount of Debris Generated during Scratching

for Various 20-nm-Thick Coatings on Al

–TiC Substrates

Coating Critical Load (mN)

Coefﬁcient

of Friction

during Scratching

SEM Observations of Scratches

Width of

Scratch (µm)

Amount of

Debris Generated

Cathodic arc carbon 19.0 0.20 0.9 Low

Ion beam carbon 10.5 0.15 0.9 Medium

PECVD carbon 9.0 0.13 1.0 Medium

DC-sputtered carbon 6.0–9.0 0.20 0.9 Medium

Ion beam–sputtered Al

Plowing

0.55 1.6 Very large

RF-sputtered SiC 12.5 0.40 1.1 Medium

–TiC substrate 7.0 0.30 1.5 Large

Tip plowed into the coating right at the beginning.

A qualitative comparison of debris generated toward the end of the scratch after catastrophic damage.

FIGURE 10.55 Initial coefﬁcient of friction of various DLC, ion beam–sputtered Al

, and RF-sputtered SiC ﬁlms

deposited on Al

–TiC substrates and the substrate, against a diamond tip (tip radius = 20 µm) and a single-crystal

sapphire ball (diameter = 3 mm) at a 10 mN normal load, 3.5 mm stroke length, 0.1 Hz frequency, 0.7 mm s

–1

average

linear speed, and under ambient temperature of 22 ± 1°C and humidity of 45 ± 5% RH. (From Gupta, B.K. and

Bhushan, B., 1995, Wear 190, 110–122. With permission.)

−

()