Bhushan B. Handbook of Micro/Nano Tribology, Second Edition

Подождите немного. Документ загружается.

where h is the vertical deﬂection, W is the force applied, l is the effective length, n is Poisson’s ratio, b

is the width, t is the thickness, and E is the Young’s modulus of the beam. As mentioned previously, the

nanoindenter records the load required to displace its own spring and the microbeam. Consequently,

the load required by the springs of the nanoindenter must be substrated from the total applied load to

determine the load on the beam. For good accuracy, the spring constant of the microbeam must be

approximately equal to or greater than 10% of the spring constant of the nanoindenter.

The application of simple beam theory to the load deﬂection data of beams also enable one to determine

the yield strength of the microbeam material. For a homogeneous cantilever beam under load, the strain

in the beam varies linearly through the thickness such that the maximum strain at a given length occurs

at the top and at the bottom of the beam. For the loading shown in Figure 10.30, the top of the beam is

in tension and the bottom of the beam is in compression. In addition, the maximum stress in the beam

is located at the ﬁxed end of the beam (B) where the applied moment is greatest. When this maximum

stress reaches the yield strength of the material, the beam begins to deform plastically. The onset of such

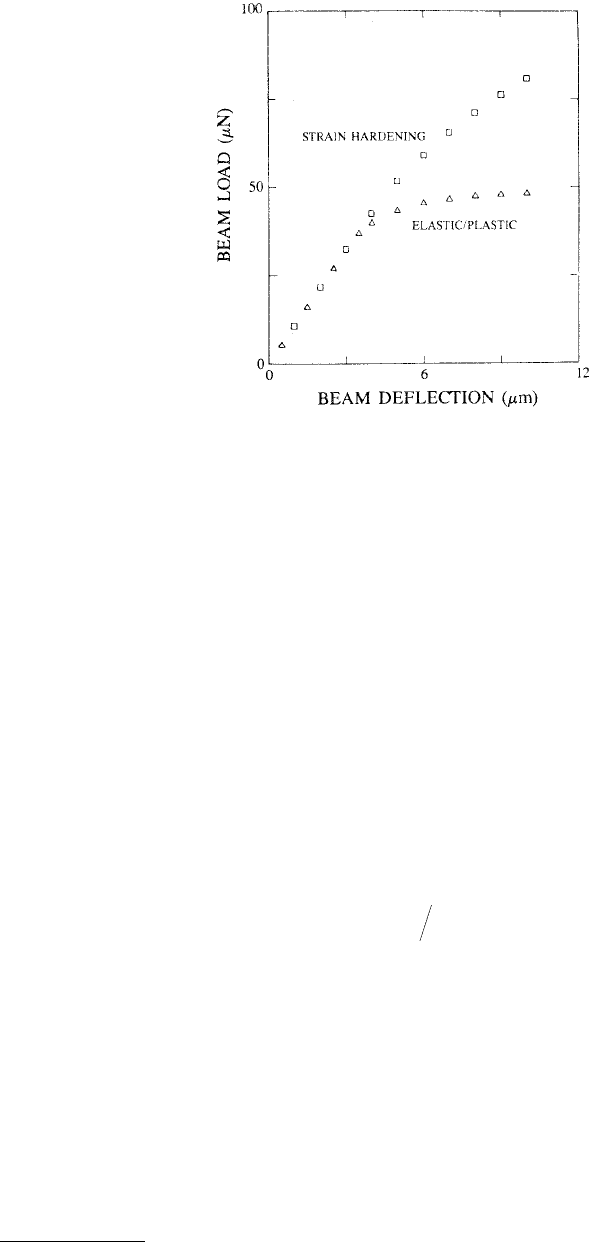
deformation can be recognized in the plot of load vs. deﬂection by a deviation from linearity, Figure 10.31.

The load that marks this deviation is deﬁned as the yield load W

, and the yield strength is given by

(10.18)

Following yielding, the beam continues to bend as more load is applied, and some of the strain in the

beam is plastic and thus unrecoverable during unloading. The shape of the load vs. deﬂection curves

after yielding and prior to unloading depends on the elastic and plastic properties of the material.

10.3.7 Determination of Hardness and Modulus of Elasticity of Thin

Films from the Composite Response of Film and Substrate

As mentioned previously, for a thin ﬁlm on a substrate, if the indentation exceeds about 30% of the ﬁlm

thickness, measured hardness is affected by the substrate properties. A number of researchers have

FIGURE 10.31 Theoretical load–deﬂection curves for cantilever beam deﬂections. The lower and upper curves

represent an elastic–plastic material and a material that strain hardens, respectively. (From Weihs, T.P. et al., 1988,

J. Mater. Res. 3, 931–942. With permission.)

Wbt=

()

attempted to derive expressions that relate thin-ﬁlm hardness to substrate hardness, composite hardness

(measured on the coated substrate) and ﬁlm thickness, and so allow the calculations of these quantities

given the remaining three (Buckle et al., 1973; Jonsson and Hogmark, 1984; Sargent, 1986; Burnett and

Rickerby, 1987b; Bhattacharya and Nix, 1988a,b; Bull and Rickerby, 1990). Here we discuss two models

based on the volume law of mixtures (volume fraction model) and ﬁnite-element simulation.

Sargent (1986) suggested that the hardness of a ﬁlm/substrate composite is determined by a weighted

average of the volume of plastically deformed material in the ﬁlm (V

) and that in the substrate (V

(10.19)

where V = V

+ V

. The deformed volumes of ﬁlm and substrate can be calculated using the expanding

spherical cavity model (Johnson, 1985). Burnett and Rickerby (1987b) found it necessary to incorporate

a further weighting factor to deforming volume to obtain a reasonable ﬁt to experimental data. This

factor accounts for the differences in relative sizes of the plastic zones in the ﬁlm and substrate.

Equation 10.19 is modiﬁed as for a soft ﬁlm on the hard substrate,

(10.20a)

and for the hard ﬁlm on the soft substrate,

(10.20b)

where X is the ratio of plastic zone volumes given as

(10.20c)

They found that n, determined empirically, ranged from ½ to ⅓.

Bhattacharya and Nix (1988a) modeled the indentation process using the ﬁnite-element method to

study the elastic–plastic response of materials. Bhattacharya and Nix (1988b) calculated elastic and plastic

deformation associated with submicron indentation by a conical indenter of thin ﬁlms on substrates,

using the ﬁnite-element method. The effects of the elastic and plastic properties of both the ﬁlm and

substrate on the hardness of the ﬁlm/substrate composite were studied by determining the average

pressure under the indenter as a function of the indentation depth. They developed empirical equations

for ﬁlm/substrate combinations for which the substrate is either harder or softer than the ﬁlm. For the

case of a soft ﬁlm on a harder substrate, the effect of substrate on ﬁlm hardness can be described as

(10.21a)

where E

and E

are the Young’s moduli, s

and s

are the yield strengths, and H

and H

are the hardnesses

of the ﬁlm and substrate, respectively. H is the hardness of the composite, h

is the contact indentation

depth, and t

is the ﬁlm thickness. Similarly, for the case of a hard ﬁlm on a softer substrate, the hardness

can be expressed as

HHX













=+ −













−

()













exp

σσ

(10.21b)

Composite hardness results were found to depend only very weakly on Poisson’s ratio (n), and for

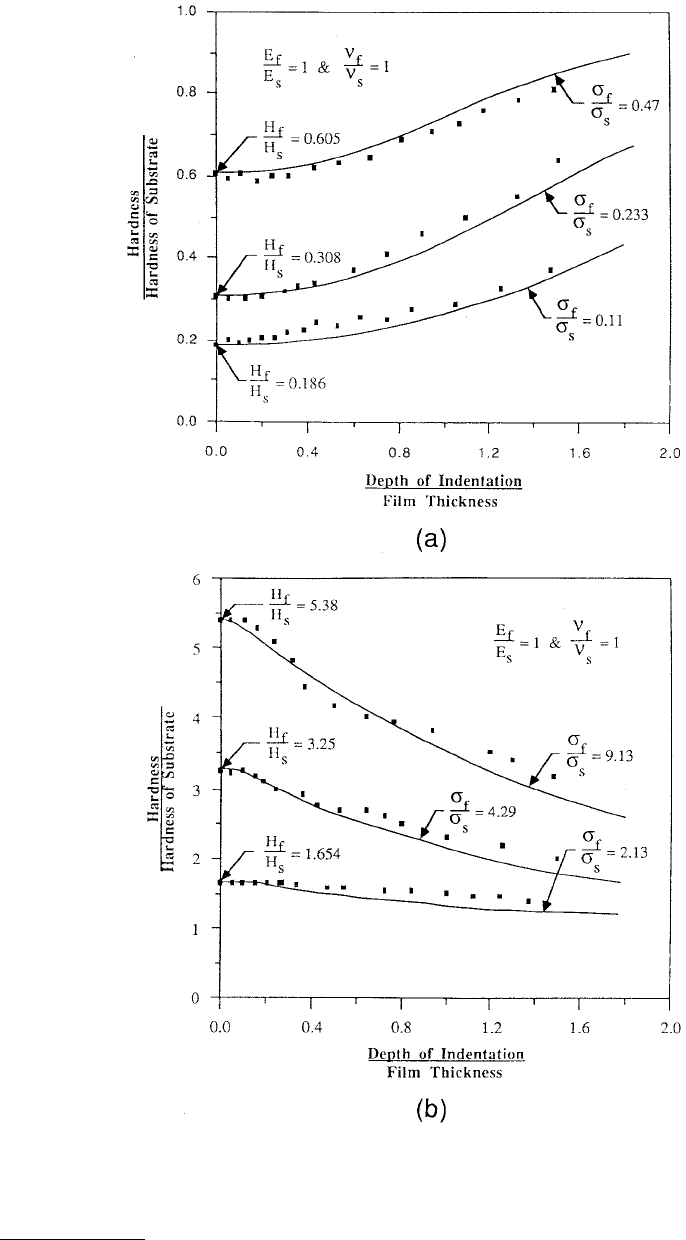
this reason, this factor was not considered in the analysis. In Figure 10.32, they show the composite

hardness results as a function of (h

) for cases in which the ﬁlm and substrate have different yield

strengths. We note that hardness is independent of the substrate for indentation depths less than about

0.3 of the ﬁlm thickness, after which the hardness slowly increases/decreases because of the presence of

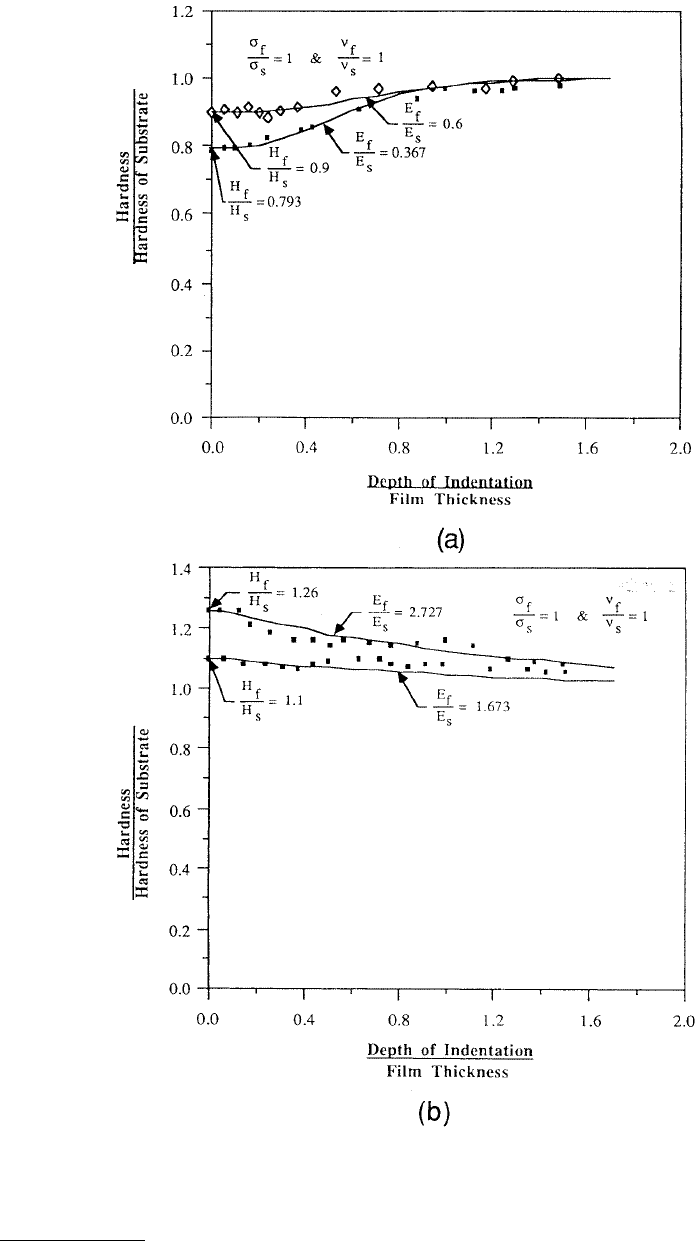
the substrate. In Figure 10.33, they show the composite hardness results for cases in which the ﬁlm and

substrate have different Young’s moduli. It is observed that the variation of hardness with depth of

indentation in these cases is qualitatively similar to cases in which the ﬁlm and substrate have different

yield strengths, although the hardness changes more gradually than in the previous cases. Burnett and

Rickerby (1987c) and Fabes et al. (1992) have applied Equations 10.19 through 10.21 to calculate the

ﬁlm hardness from the measured data for various ﬁlms and substrates.

Doerner and Nix (1986) empirically modeled the inﬂuence of the substrate on the elastic measurement

of very thin ﬁlm in an indentation test using the following expression for the compliance:

(10.22)

where the subscripts f, s, and i refer to the ﬁlm, substrate, and indenter, respectively. The term is

equal to (24.5)

1/2

for the Vickers or Berkovich indenter. The ﬁlm thickness is t

, and b is the y-intercept

for the compliance vs. 1/depth plot, obtained for the bulk substrate, which can be neglected in most

cases. The weighing factors [1 – exp(at

/ ] and exp(–at

/ ) have been added to account for the

changing contributions of the substrate and ﬁlm to the compliance. The factor a can be determined

empirically.

King’s analysis (1987) veriﬁed that Equation 10.22 is an excellent functional form for describing the

inﬂuence of the substrate and theoretically determined the values of a for various indenter shapes. The

value of a was found to depend on the indenter shape and size and ﬁlm thickness and was found to be

independent of E

. The values of a as a function of /t

for Berkovich (triangular) indenters are

shown in Figure 10.34. The values of a are found to be similar for square and triangular indenters.

Bhattacharya and Nix (1988b) analyzed the deformations of a layered medium in contact with a conical

indenter using the ﬁnite-element method. Their analysis also veriﬁed the relationship given in

Equation 10.22.

10.4 Examples of Measured Mechanical Properties

of Engineering Materials

To illustrate the usage of nanoindentation techniques, we present typical data obtained on various

materials, coatings, and surface treatments.

10.4.1 Load — Displacement Curves

A variety of mechanical phenomena, such as transition from elastic to plastic deformation, creep defor-

mation, formation of subsurface cracks, and crystallographic phase transition, can be studied by the

load–displacement curves obtained at different loading conditions (Pethica et al., 1983; Doerner and Nix,

1986; Stone et al., 1988; LaFontaine et al., 1990c, 1991; Pharr et al., 1990; Page et al., 1992; Oliver and

fsfs

=+ −













−

()

()()

()













exp

σσ

dW A E













−

























−













−





















να

exp exp

A A

FIGURE 10.32 Effect of relative yield strengths of the ﬁlm and the substrate on the composite hardness for (a) a

soft ﬁlm on a hard substrate and (b) a hard ﬁlm on a soft substrate. (From Bhattacharya, A.K. and Nix, W.D., 1988,

Int. J. Solids Struct. 24, 1287–1298. With permission.)

FIGURE 10.33 Effect of relative Young’s moduli of the ﬁlm and the substrate on the composite hardness for (a) a

soft ﬁlm on a hard substrate and (b) a hard ﬁlm on a soft substrate. (From Bhattacharya, A.K. and Nix, W.D., 1988,

Int. J. Solids Struct. 24, 1287–1298. With permission.)

Pharr, 1992; Pharr, 1992; Whitehead and Page, 1992; Gupta et al., 1993, 1994; Gupta and Bhushan, 1994,

1995a,b; Bhushan et al., 1995, 1996, 1997; Bhushan and Gupta, 1995; Patton and Bhushan, 1996; Bhushan

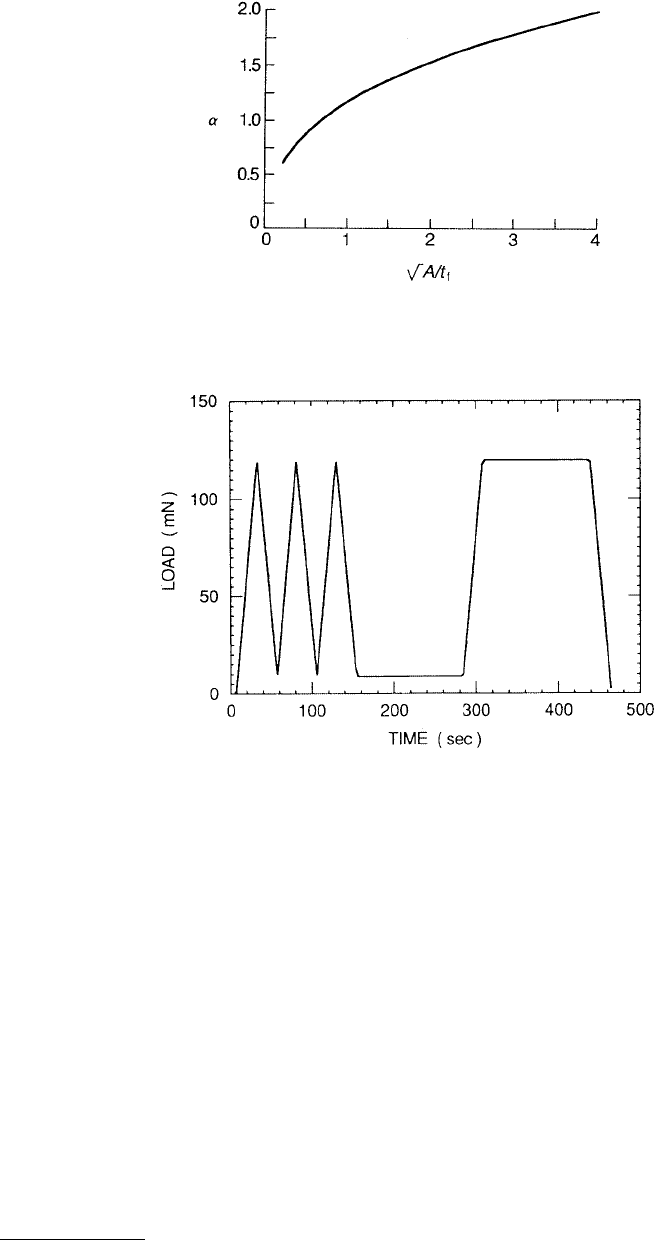
and Li, 1997; Li and Bhushan, 1998b, c). The load–time sequence used by Oliver and Pharr (1992) for

study of various materials included three loading–unloading cycles, hold for 100 s at 10% of the peak

load, reload, hold for 100 s, and unload, Figure 10.35. Load–displacement curves for mechanically

polished single-crystal aluminum, electropolished single-crystal tungsten, soda lime glass, fused silica

and (110) single-crystal silicon are shown in Figures 10.36 through 10.40. Silicon included only two

loading–unloading cycles (Figure 10.40). The softest material is aluminum, with peak depth of almost

5000 nm at 120 mN load, while the hardest is silicon which was penetrated to a depth of only about

800 nm. Both the aluminum and tungsten data are typical of materials in which the hardness is relatively

small compared to the modulus, as is observed in most metals; most of the indenter displacement in

these metals is accommodated plastically and only a small portion is recovered on unloading. Soda lime

glass, fused silica, and silicon are harder which show larger elastic recovery during unloading, the largest

being that for fused silica.

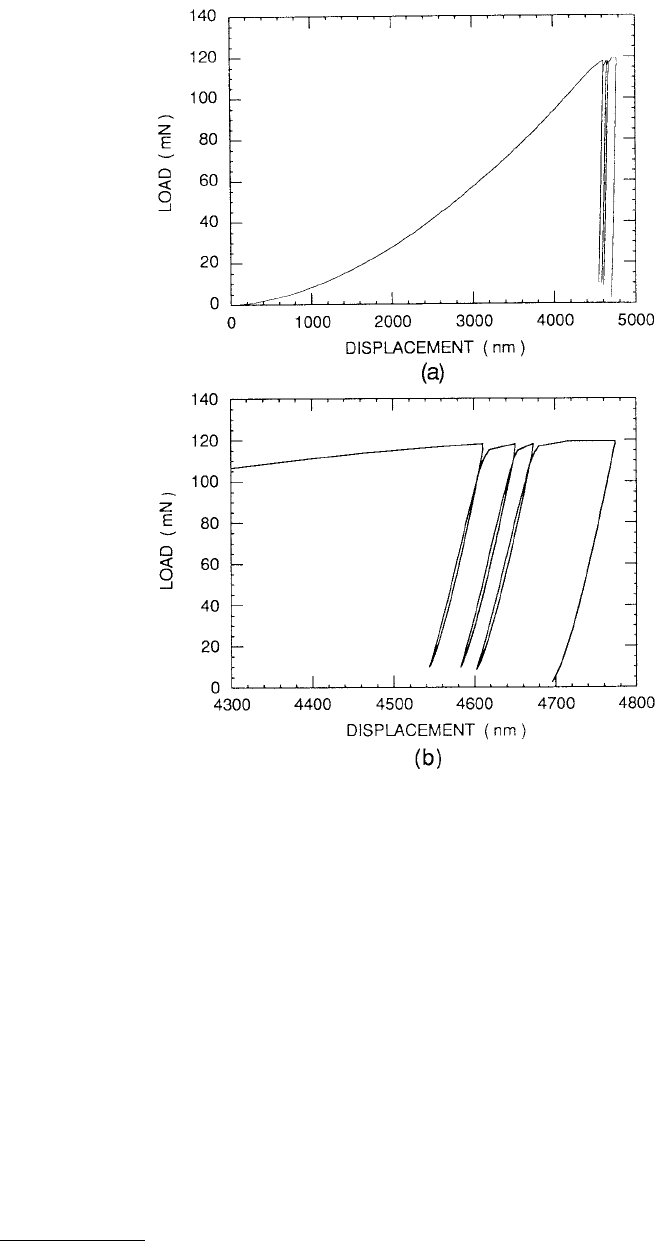
The unloading/reloading behaviors of the various materials are different. For aluminum, the expanded

view in Figure 10.36b shows that the peak load displacements shift to higher values in successive

FIGURE 10.34 Parameter a as a function of normalized indenter size for a Berkovich indenter indenting a layered

solid surface. (From King, R.B., 1987, Int. J. Solids Struct. 23, 1657–1664. With permission.)

FIGURE 10.35 A typical load–time sequence; peak load = 120 mN. (From Oliver, W.C. and Pharr, G.M., 1992,

J. Mater. Res. 7, 1564–1583. With permission.)

loading/unloading cycles. In addition, the relatively large displacement just prior to ﬁnal unloading is

due to creep during the 100-s hold period at peak load. At 120 mN, the indentation depth in tungsten

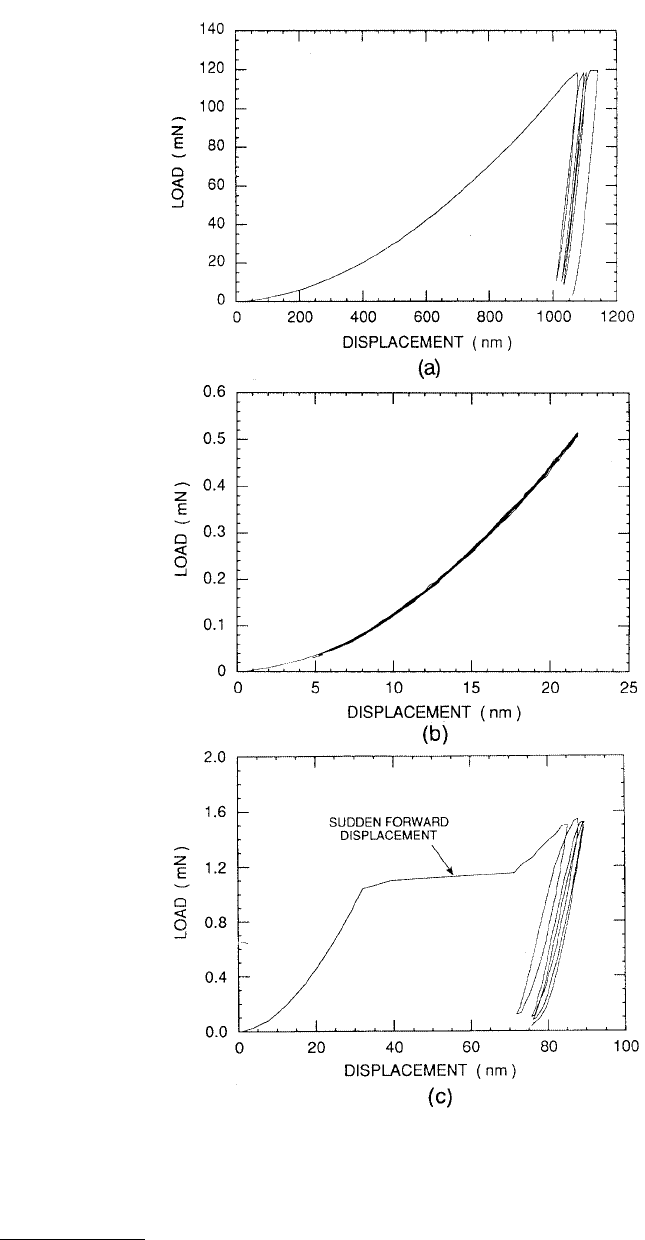
is about one fourth of that in aluminum, Figure 10.37a. However, the behavior of tungsten is similar to

that of aluminum. Indentation at a very low load of 0.5 mN caused only elastic displacements,

Figure 10.37b. At higher peak loads, the indentation is not just elastic, Figure 10.37c. When a threshold

load of about 1 mN is reached, a sudden jump in displacement corresponding to the onset of plasticity

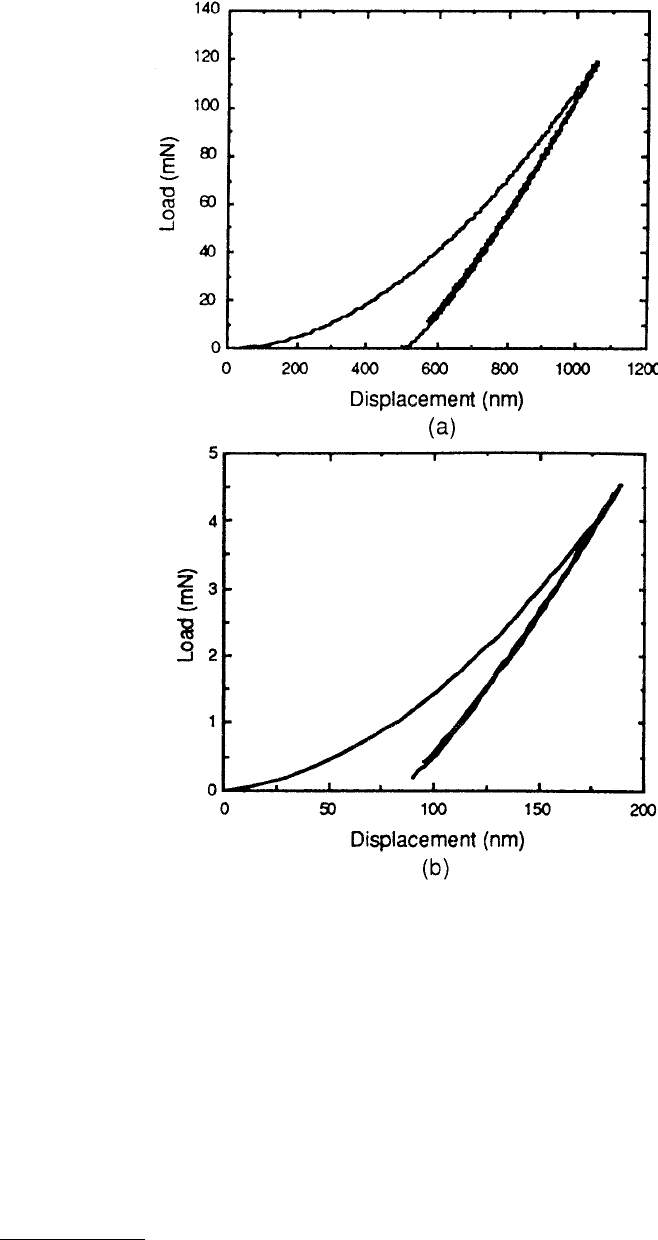
is observed, and a permanent hardness impression is formed. Soda lime glass (Figure 10.38) and tungsten

at low loads (Figure 10.37c) exhibit distinct hysteresis loops, as might be expected if there were a small

amount of reverse plasticity upon loading. However, the looping degenerates with cycling after three or

four cycles, the load–displacement behavior is largely elastic. The unloading/reloading curves for fused

silica are nearly the same, Figure 10.39. The near-perfect reversibility suggests that at peak loads of 120

and 4.5 mN, deformation after initial unloading is almost entirely elastic.

The behavior of silicon shown in Figure 10.40, is in sharp contrast to other materials (e.g., fused silica

data shown in Figure 10.39) (Pharr et al., 1989, 1990; Page et al., 1992; Pharr, 1992). The data presented

FIGURE 10.36 (a) Load vs. displacement plot for an mechanically polished single-crystal aluminum, (b) an

expanded view of the unloading/reloading portion of the load vs. displacement data. (From Oliver, W.C. and Pharr,

G.M., 1992, J. Mater. Res. 7, 1564–1583. With permission.)

FIGURE 10.37 Load vs. displacement plot for an electropolished single-crystal tungsten (a) at a peak load of

120 mN, (b) at a peak load of 0.5 mN (elastic contact), and (c) at a peak load of 1.5 mN showing the yield point.

(From Oliver, W.C. and Pharr, G.M., 1992, J. Mater. Res. 7, 1564–1583. With permission.)

in Figure 10.40 were taken over two cycles of loading and unloading. At high peak loads, the initial

unloading curve for silicon is not at all smooth, but exhibits a sharp discontinuity caused by the surface

of the specimen being suddenly thrust outward, Figure 10.40a. At lower peak loads, the behavior changes,

and below some critical value the discontinuity is no longer observed, Figure 10.40b. However, at this

load the load–displacement behavior shows another anomalous feature — a large hysteresis which shows

no sign of degeneration through several cycles of deformation. The fact that the curves are highly

hysteretic implies that deformation is not entirely elastic. The discontinuity at high loads and the

nondegenerative hysteresis at low loads are quite unique to silicon and are observed in each of the (100),

(110), and (111) orientations. The load below which the discontinuity disappears and the hysteresis

becomes apparent is generally in the range 5 to 20 mN. Pharr (1992) concluded that larger hysteresis

observed in the unloading curve at low loads is due to a pressure-induced phase transformation from

its normal diamond cubic form to a b–tin metal phase (Figure 10.41). At some point in the transforma-

tion, an amorphous phase is formed whose evidence is reported by Callahan and Morris (1992). The

FIGURE 10.38 (a) Load vs. displacement plot for a soda lime glass and (b) an expanded view of the unload-

ing/reloading portion of the load vs. displacement data. (From Oliver, W.C. and Pharr, G.M., 1992, J. Mater. Res. 7,

1564–1583. With permission.)

discontinuity in displacement observed during unloading at peak loads of greater than about 15 mN is

due to formation of a lateral crack which forms at the base of the median crack (Figure 10.41). Lateral

cracking is aided by the phase transformations.

Weihs et al. (1992) indented Si(100) with 120 mN of load. The load–displacement curve is shown in

Figure 10.42a and the ﬁrst AE signal that was recorded for this test is shown in Figure 10.42b. The AE

signals were sharp and they correlated with small jumps in tip displacement. The rise time for the signal

in Figure 10.42b is 1.5 µs. After testing, radial cracks were visible at the corners of indentation. AE events

such as the one shown in Figure 10.42b were recorded at applied load as low as 48 mN on loading. In

the ﬁnal stages of unloading, small AE signals that had an inverted shape compared with Figure 10.42b

FIGURE 10.39 Load vs. displacement plots for fused silica (a) at a peak load of 120 mN and (b) at a peak load of

4.5 mN. (From Pharr, G.M., 1992, in Thin Film: Stresses and Mechanical Properties III, W.D. Nix et al., eds., Vol. 239,

pp. 301–312, Materials Research Society, Pittsburgh. With permission.)