Birge J.R., Louveaux F. Introduction to Stochastic Programming

Подождите немного. Документ загружается.

394 9 Monte Carlo Methods

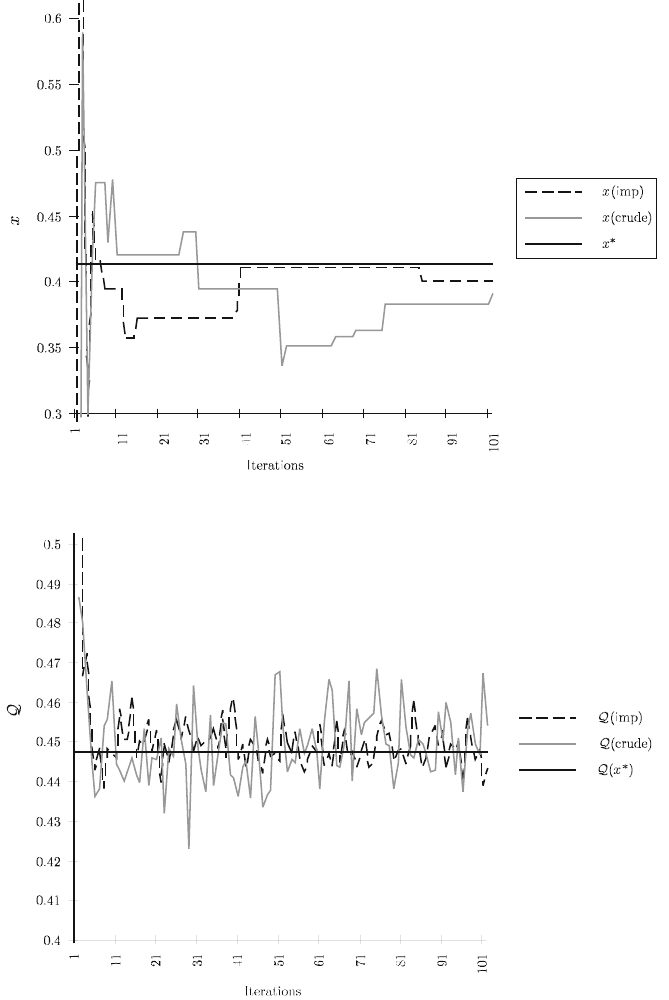
Fig. 1 Solutions for crude Monte Carlo and importance sampling.

Fig. 2 Objective values for crude Monte Carlo and importance sampling.

9.2 Stochastic Decomposition 395

The results in Figures 1 and 2 indicate that sampled cuts in the L -shaped method

can produce fairly accurate results but that convergence to optimal values may re-

quire large numbers of samples for each cut even for small problems and may yield

inaccurate results with independent samples for each cut due to the bias issue. This

difﬁculty is particularly an issue if initial cuts are generated with small numbers

of samples since these may be particularly inaccurate and limit convergence unless

they are removed in favor of more accurate cuts. A procedure to avoid this problem

is gradually to remove initial cuts as the algorithm progresses. This is the intent of

the approach in the next section.

Exercises

1. Show how to sample from the density g

(

) as the sum of the absolute values

|x −

|, i = 1,2 for Example 1.

2. Consider Example 1 in Section 5.1 with ξ uniformly distributed on [1,5] .Ap-

ply the crude Monte Carlo L -shaped method to this problem for 100 iterations

with 100 samples per cut. What would the result be with importance sampling

in this case?

3. Apply both the crude Monte Carlo and importance sampling approaches to

Example 1 with both x

and x

decision variables. First, use 100 samples for

each cut for 100 iterations and then compare to results with an increase to 500

samples per cut.

9.2 Stochastic Decomposition

An alternative approach to using cuts produced with multiple samples in the L -

shaped method is to use cuts constructed from small but increasing numbers of

samples. This approach from Higle and Sen [1991b] generates many cuts with small

numbers of additional samples on each cut and adjusts these cuts to drop away as the

algorithm continues processing. The method is called stochastic decomposition.We

will give a basic development here and refer to Higle and Sen [1996] for more de-

tails. For simplicity, we assume complete recourse, a known (probability one) lower

bound on Q(x,

) (e.g., 0 ), and a bounded set of dual solutions to the recourse

problem (3.1.1). We also assume that K

and

are compact.

With these assumptions, the basic stochastic decomposition method generates

iterates, x

, and observations,

. We can state the basic stochastic decomposition

method in the following way.

Basic Stochastic Decomposition Method

Step 1.Set

= 0,

,andlet x

solve

396 9 Monte Carlo Methods

min

Ax=b,x≥0

x + Q(x,

)} . (2.1)

Step 2.Let

+1andlet

be an independent sample generated from ξ .Find

∑

s=1

Q(x

∑

s=1

(

)

(

−Tx

) .Let E

∑

s=1

(

)

and e

∑

s=1

(

)

Step 3. Update all previous cuts by E

←

−1

and e

←

−1

for s = 1,...,

−

Step 4.Solvethe L -shaped master problem as in (1.8) to obtain x

.GotoStep2.

This method differs slightly from the basic method in Higle and Sen [1991b] in

our assuming

to be optimal dual solutions in each iteration. Higle and Sen allow

a restricted set of dual optima that may decrease the solution effort (with perhaps

fewer effective cuts).

The main convergence result is contained in the following theorem.

Theorem 1. Assuming complete recourse, Q(x,

) ≥ 0 , bounded dual solutions to

(3.1.1), K

and

compact, there exists a subsequence, {x

}, of the iterates of the

basic stochastic decomposition method such that every limit point of {x

} solves

the recourse problem (3.1.1) with probability one.

Proof: We follow the proof of Theorem 4 in Higle and Sen [1991b]. We use their

Theorem 3 (Exercise 1), which gives the existence of a subsequence of {x

} such

that

lim

→∞

− max

l=1,...,

−1

−E

−1

)=0 . (2.2)

Suppose {x

} is a subsequence of the subsequence achieving (2.2) such that

lim

= ˆx where A ˆx = b , x ≥ 0 . This occurs for some subsequence by com-

pactness. From x

∗

optimal,

∗

+ Q(x

∗

) ≤c

ˆx + Q( ˆx) . (2.3)

Note that because Q(x,

) ≥ 0forall

∈

and Q(x,

) ≥

−Tx) for any

W ≤ q and any sample

,forany 1≤ s ≤

∑

i=1

Q(x,

) ≥

∑

i=1

−Tx) , (2.4)

where

is any feasible multiplier in the recourse problem for

.From(2.4), it

follows that

∑

i=1

Q(x,

) ≥ e

−E

x for all l and

,where E

and e

are

the components of Cut l on Iteration

. Therefore,

9.2 Stochastic Decomposition 397

x + max

l=1,...,

−E

x) ≤ c

x +

∑

i=1

Q(x,

) . (2.5)

increases,

∑

i=1

Q(x,

) → Q(x) ,so

limsup

∗

+ max

l=1,...,

−E

∗

)] ≤ c

∗

+ Q(x

∗

) , (2.6)

with probability one. We can also show that (Exercise 2)

lim

+ max

l=1,...,

−E

)=c

ˆx + Q( ˆx) , (2.7)

with probability one. Thus, (2.6), (2.7), and the fact that x

minimizes c

x +

max

l=1,...,

−1

−E

−1

x) over feasible x yield

∗

+ Q(x

∗

) ≤ c

ˆx + Q( ˆx)

≤ limsup

∗

+ max

l=1,...,

−E

∗

)]

≤ c

∗

+ Q(x

∗

) , (2.8)

which proves the result.

One difﬁculty in this basic method is that convergence to an optimum may only

occur on a subsequence. To remedy this, Higle and Sen suggest retaining an in-

cumbent solution that changes whenever the objective function falls below the best

known value so far. The incumbent is updated each time a sufﬁcient decrease in the

th iteration objective value is obtained. They also show that the sequence of in-

cumbents contains a subsequence with optimal limit points, and then show how this

subsequence can be identiﬁed. Various approaches may be used for practical stop-

ping conditions, such as the statistical veriﬁcation tests for optimality conditions in

Higle and Sen [1991a].

Example 1 (continued)

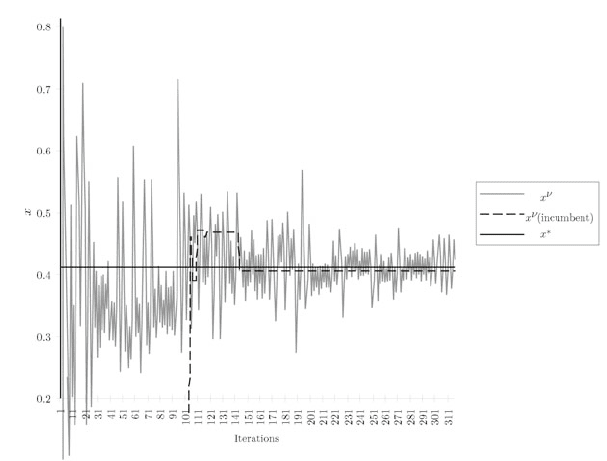
We again consider Example 1 from Section 8.2. The basic stochastic decomposition

method results appear in Figures 3 and 4. In Figure 3, both the basic result x

and the incumbent solution, x

(incumbent), which is adjusted whenever a solution

after the ﬁrst 100 iterations improves the previous best estimate by 1%. Figure 3

also gives the optimal solution, x

∗

. The total number of iterations yields about

50,000 subproblem solutions, which is approximately equal to the total number of

iterations in Figures 1 and 2. Note that the raw solutions x

oscillate rapidly, while

the incumbent solutions settle close to x

∗

quite quickly after their initiation at

100 .

398 9 Monte Carlo Methods

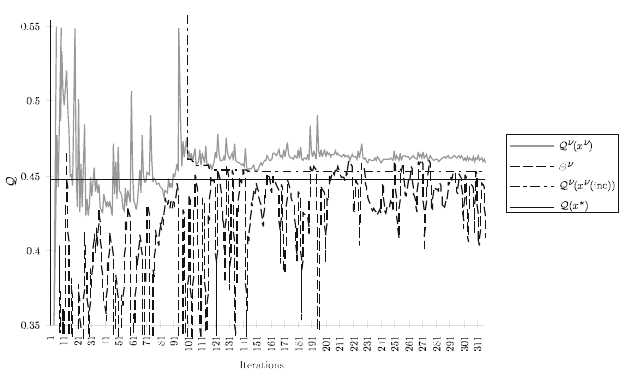
The objective value estimates,

, Q

,and Q

(inc)) for the incumbent,

and the optimal objective value, Q(x

∗

) , appear in Figure 4. Note that the

values

from the master problem have wide oscillations. The Q

) values have lower but

signiﬁcant variation. The incumbent objective values, however, show low variation

that begins to approach the optimum.

Fig. 3 Solutions for the stochastic decomposition method.

Exercises

1. Prove Theorem 1. Show ﬁrst that eventually the objective value of (1.8)for x

at iteration

is the same as the objective value of (1.8)for x

at iteration

n−1

2. Prove that there exists a subsequence of iterates {x

} in the basic stochastic

decomposition method with the assumptions so that (2.2) holds.

3. Suppose a subsequence of iterates x

→ ˆx in the basic stochastic decomposi-

tion method. Prove that (2.7) holds.

4. Apply the basic stochastic decomposition method to Example 1 in Section 5.1

with ξ uniformly distributed on [1,5] . Record the sequence of iterations until

10 consecutive iterations are within 1% of the optimal objective value.

9.3 Stochastic Quasi-Gradient Methods 399

Fig. 4 Objective values for the stochastic decomposition method.

9.3 Stochastic Quasi-Gradient Methods

Stochastic quasi-gradient methods represent one of the ﬁrst computational devel-

opments in stochastic programming. They apply to a broad class of problems and

represent extensions of stochastic approximation methods (see, e.g., Dupaˇc [1965]

and Kushner [1971]). Our treatment will be brief because the emphasis in this book

is on methods that exploit the structure of deterministic equivalent or approximation

problems. Ermoliev [1988] provides a more complete survey of these methods.

Stochastic quasi-gradient methods (SQG) apply to a general mathematical pro-

gram of the form:

min

x∈X⊂ℜ

(x)

s. t. g

(x) ≤ 0 , i = 1,...,m , (3.1)

where we assume that each g

is convex. We suppose that an initial point, x

∈ X ,

is given. The method generates a sequence of points, {x

}, that converges to an

optimal solution of (3.1).

Given a history at time

, (x

,...,x

) , the method selects function estimates,

(

) , and subgradient estimates, β

(

) , such that

E[η

(

) | (x

,...,x

)] = g

)+a

(

) (3.2)

and

E[β

(

) | (x

,...,x

)] + b

(

) ⊂

∂

) , (3.3)

400 9 Monte Carlo Methods

where a

(

) , b

(

) may depend on (x

,...,x

) but must satisfy

(

) → 0andb

(

)→0 . (3.4)

When b

(

) = 0, β

(

) is called a stochastic quasi-gradient.Otherwise, β

(

) is

a stochastic subgradient.

We ﬁrst consider the method when all constraints are deterministic and repre-

sented in X. Thus, Problem 3.1 becomes

min

x∈X⊂ℜ

(x) . (3.5)

The method requires a projection onto X represented by

∏

(y)=argmin

{x −y

| x ∈ X} .

In the basic method, a sequence of step sizes {

} is given. The stochastic quasi-

gradient method deﬁnes a stochastic sequence of iterates, { x

},by

∏

−

(

)] , (3.6)

where we interpret the projection as operating separately on each element

∈

so that x

(

∏

[(x

(

) −

(

)(

))] .

To place all these results into the two-stage recourse problem as in (1.1.2), let

X = {x |Ax = b, x ≥0} , g

(x)=



(x,ξ)P(dξ) where

(x,ξ)=inf

y |W y = h−Tx, y ≥ 0} .

Thus, we can use β

(x) such that β

(x)

− T

x)=g

(x,ξ

) ,

(x) ≤ q

for a sample ξ

composed of the components, h

, T

,and q

The stochastic quasi-gradient method takes a step in this direction and then projects

back onto X . In the following example and the exercises, we explore the use of this

approach.

For these examples, we use an estimate of the objective value by taking a moving

average of the last 500 samples, Q

−ave

∑

499

i=0

Q(x

−i

)/500 . Changes

in this estimate (or the lack thereof) can be used to evaluate the convergence of

stochastic quasi-gradient methods. Gaivoronski [1988] discusses various practical

approaches in this regard.

Example 1 (continued)

We consider the same example and apply the stochastic quasi-gradient method. On

each step

, a random sample

is taken with

(

) ∈

∂

Q(x

) .For X = {x |

0 ≤x ≤1}, the projection operation yields x

= min(1,max(x

(

),0)) .

9.3 Stochastic Quasi-Gradient Methods 401

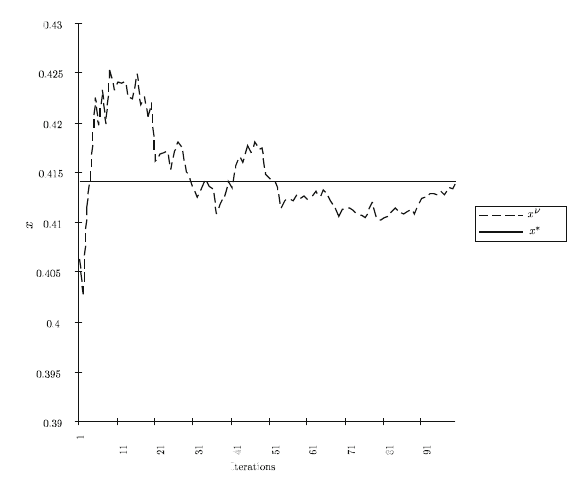
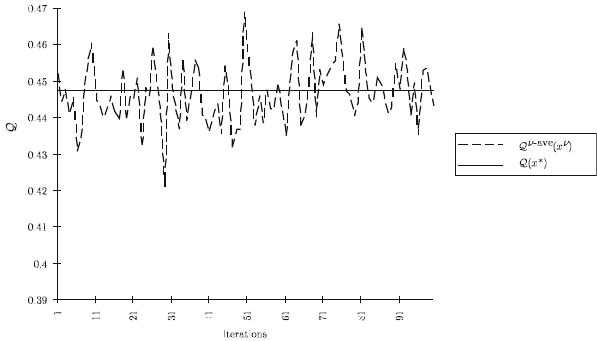
Figures 5 and 6 show these iterations for solutions x

and objective estimates,

−ave

for every multiple of 500 iterations up to 50,000 so that total numbers of

recourse problem solutions are the same as in Figures 1 to 4.

Fig. 5 Solutions for the stochastic quasi-gradient method.

Note that the iterations in Figure 5 appear to approach x

∗

much more quickly

than the results in Figures 1 to 4. They also seem to show lower variances in the

objective estimates in Figure 6, although these results are not converging to zero

variance because the sample length 500 is not changing. To achieve convergence

or greater conﬁdence in a solution, the number of samples in the estimate must

increase.

While the results in Figures 5 and 6 indicate that stochastic quasi-gradient meth-

ods may be more effective than the decomposition methods, we should note that

this example is quite low in dimension. For higher dimensions, the results are often

quite different. In general, stochastic quasi-gradient methods exhibit similar behav-

ior to subgradient optimization methods that often have slow convergenceproperties

in higher dimensions. They are, nonetheless, easy to implement and can give good

results, especially in small problems.

In the rest of this section, we discuss the theory behind the stochastic quasi-

gradient method convergence. The exercises consider examples for using SQG.

The basic method in (3.6) traces back to the unconstrained methods of Robbins-

Monro [1951]. The main device in demonstrating convergence of {x

} to a point

402 9 Monte Carlo Methods

Fig. 6 Objective values for the stochastic quasi-gradient method.

in X

∗

is the use of a stochastic quasi-Feyer sequence (see Ermoliev [1969]), a

sequence of random vectors, {w

},deﬁnedin (

,P) such that for a set W ⊂

ℜ

,E[w



] < +∞ ,andany w ∈W ,

E{w −w



| w

,...,w

}≤w −w



+ γ

= 0,1,... ,

≥ 0 ,

∞

∑

E[γ

] < +∞ . (3.7)

The following result shown in Ermoliev [1976] is the basis for the convergence

results.

Theorem 2. If {w

} is a stochastic quasi-Feyer sequence for a set W , then

(a) {w −w



} converges with probability one for any w ∈W , and E[w −



] < c < +∞ ;

(b) the set of limit points of {w

(

)} is nonempty for almost all

∈

;

(

) and ¯w

(

) are two distinct limit points of {w

(

)} such that

¯w

(

) ∈ W, ¯w

(

) ∈ W,then W⊂ H , a hyperplane such that

= {w |

w =

},  ¯w

(

) −

∏

( ¯w

(

)) =  ¯w

(

) −

∏

( ¯w

(

)),where

∏

denotes projections onto

With this result, we can obtain the most basic convergence result, given below

without proof.

Theorem 3. Given the following:

9.3 Stochastic Quasi-Gradient Methods 403

(a) g

(x) is convex and continuous,

(b) X is a convex compact set,

, and γ

(

)= inf

∗

∈X

∗

(

)

−x

∗

) , satisfy with proba-

bility one,

> 0 ,

∞

∑

=+∞ ,

∞

∑

| γ

(

) | +(

)

β

(

)

] < ∞ , (3.8)

then, with probability one, for any ¯x(

)=lim

(

) , ¯x(

) ∈ X

∗

The general method can be ampliﬁed in a variety of ways. Condition (c) can

be relaxed to remove the ﬁniteness of

∞

∑

when

(

)=0forall

,butthe

convergence is for

∑

(see Uriasiev [1988]).

Two important aspects of stochastic quasi-gradient implementations are the de-

terminations of step sizes and stopping rules. Various adaptive step sizes are consid-

ered by Mirzoachmedov and Uriasiev [1983]. For stopping rules, we refer to Pﬂug

[1988], where details appear. The results describe the use of stopping times {

to yield uniform asymptotic level

conﬁdence regions,deﬁnedby

lim

→0

inf

P{x

−x

∗

≤

}≥1 −

. (3.9)

Deterministic step size rules do not, unfortunately, produce such uniform conﬁdence

intervals. Instead, Pﬂug shows that an oscillation test stopping rule does obtain such

conﬁdence regions. In this rule, a test is performed to check whether the iterates are

oscillating without objective improvement. The key is building consistent estimates

of the objective Hessian at x

∗

and the covariance matrix of objective errors. For

other issues concerning implementation, we refer to Gaivoronski [1988].

The use of sample subgradients can also produce results for efﬁcient computation

with some conﬁdence level. Nesterov and Vial [2008] give one of these results for

a stochastic subgradient method in which the values of multiple algorithm paths are

combined to achieve efﬁcient computation. Dyer,Kannan, and Stougie [2002] and

Shmoys and Swamy [2006] both use stochastic subgradients in a different way to

deﬁne regions of improvement over which the ellipsoid optimization method can be

applied. Combining this approach and a search step can for many stochastic linear

programs in fact ﬁnd a solution within

of optimal with effort on the order of

and a factor depending on the problem input size (Shmoys and Swamy [2006]).