Blank L., Tarquin A. Engineering Economy (McGraw-Hill Series in Industrial Engineering and Management)
Подождите немного. Документ загружается.


SECTI
ON
14.
2 Pr
ese
nt Worth
Ca
lc
ul
ations Adjust
ed
for Infla
ti
on
TABLE
14-1
Inflation Calc
ul
ations Using Constant-Value Do
ll
ars
(f=
4%, i = 10%)
Cost
Increase
Cost
in
Future
Cost
in
Present
Worth
Year
Due
to
4%
Future
Constant
-Value
at
Real
n Inflation Dollars
Dollars
;=10%
(1
)
(2)
(3)
(4)
= (3}/ 1.
04
n
(5)
= (4)(P/ F,10%,n)
0 $5000 $5000 $5000
$5000(0.04)
= $200 5200 5200/(1.04)1 = 5000 4545
2
5200(0.04) = 208 5408
5408
/(
1.
04i = 5000
4132
3
5408(0.04) = 216 5624 5624
/(
1.04)3 = 5000
3757
4
5624(0.04)
= 225 5849 5
849/(
1.04
)4
= 5000 3415
shows
the
present
worth
of
future
amounts
of
$
5000
at
a real
interest
rate
of
i =
10
% per year.
Two
conclusions
ca
n be made.
Atf
= 4%, $
5000
today
inflates to
$5849
in
4 years. And $
5000
four years from
now
has a
PW
of
only
$3
415
constant
-value
dollars
at
a real interest rate
of
10
%
per
year.
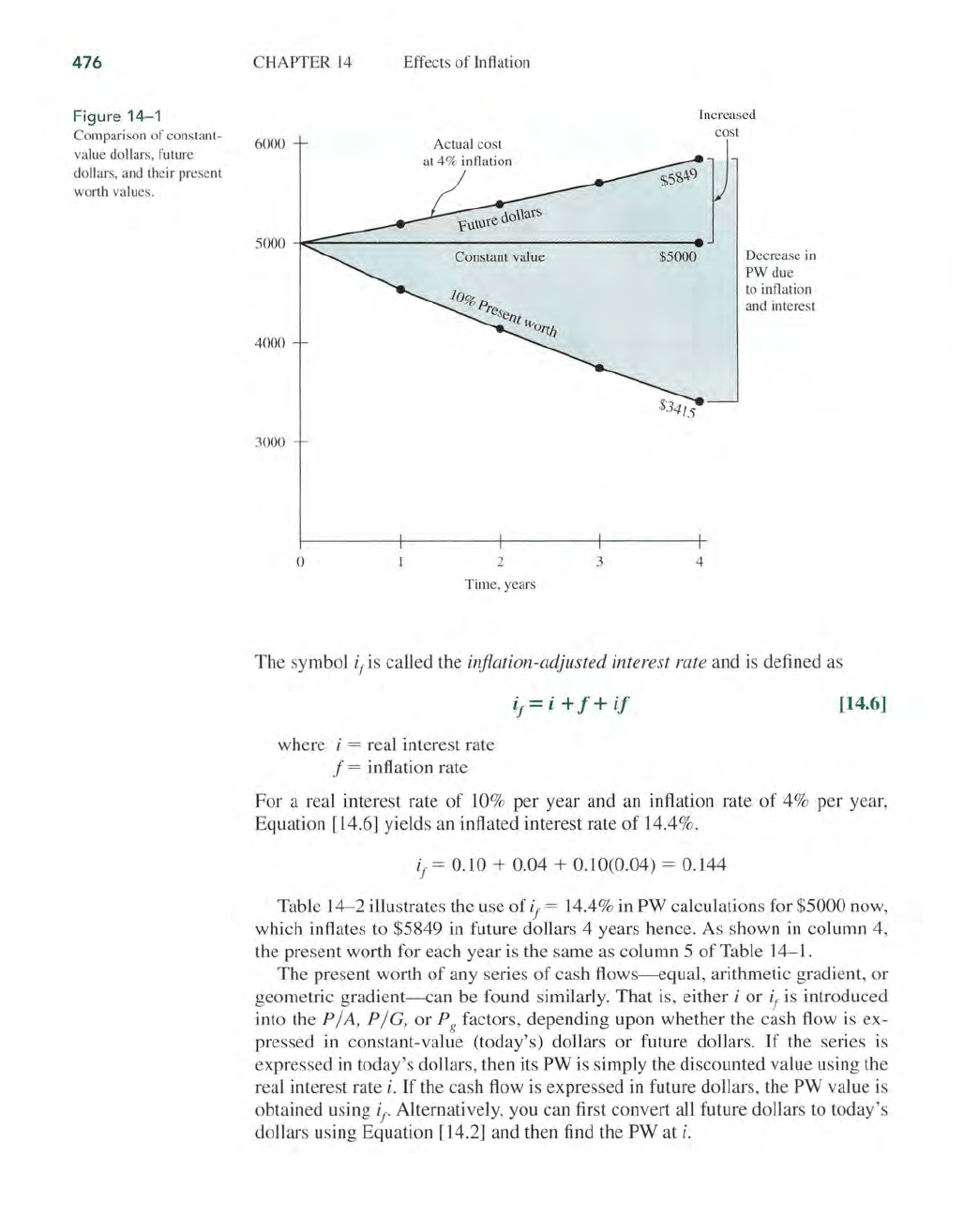
Fi
gure
14
- 1
shows
the differences
over
a
4-year
period
of
the
constan
t
-va
lue
amount
of
$5000
, the future-dollar costs at 4% inflation, and the
present
worth
at
10% real interest with inflation
considered.
The
effect
of
compounded
inflation
and
intere
st rates is large, as
you
can
see
by the s
haded
area.
An al
ternative
, and l
es
s
co
mplic
ated,
method
of
accounting
for
inflation in
a
present
worth
analys
is involves
adjusting
the
interest
formulas
themselve
s to
account
for
inflation.
Con
sider the P / F formula,
where
i is the real i
nterest
rate.
P = F
---
(I
+ i)"
The F is a future-dollar
amount
with inflation built in.
And
F
can
be
converted
into today's
do
llars by us
in
g Equation [14.2].
P = F 1
(J +
f)"
(l
+ i)"
= F
------
--
-----
(1 + i + f + i
n"
[14.4]
If
the term i + f +
if
is defined as iI' the
equation
become
s
1
P = F =
F(P
/ F,iI,n)
(1
+
9"
[14.5]
475
( Ch3
P
-)
2
476
Figure 14-1
Compa
ri
son of
co
ns
ta
nt
-
value do
ll
ars, fut ure
do
ll
ars, a
nd
th
eir present
wor
th
va
lu
es.
CH
APTER
14
6000
Effects of Inflation
Actual cost
at
4%
in
fl
ation
In
creased
co
st
$5
\',
49
l )
5000
~~--------
--------------
-------------e
J'
Constant value
4
000
3
000
o
2
Ti me, yea
rs
$
5000
3
4
Decrease
in
P
Wdu
e
to
in
fl
a
ti
on
and interest
The symbol if is called the
infl
a
ti
on-a
djus
ted
int
erest
ra
te and is de
fin
ed as
where
i = real interest rate
f = inflation rate
[14.6]
F
or
a re
al
interest rate of 10% per year and an inflation rate of 4% per year,
Equation [14.6] yields an inflated interest rate
of
14.4
%.
if = 0.
10
+ 0.04 + 0.
10
(0.
04
) = 0.144
Table
14-
2 illustrates the use
of
if = 14.4% in
PW
calcula
ti
ons for $5000 now,
which inflates to $5849 in future dollars 4 years hence. As shown
in
column 4,
the present worth for each year is the s
am
e as column 5
of
Table
14-1.
The present worth
of
any series
of
cash
fl
ows-e
qual, arithme
ti
c gradient, or
geometric gradient
-ca
n be found similarl
y.
That is, either i
or
if is introduced
into the
Pi A, p
iG,
or
P
g
factors, de
pe
nding upon whether the cash flow is ex-
pressed
in
constant-value (today's) dollars
or
future dollars.
If
the se
ri
es is
expressed
in
today's dollars, then its
PW
is simply the discounted value us
in
g the
real interest rate
i.
If
the cash
fl
ow is expressed in future do
ll
ars, the
PW
va
lu
e is
obtained using
i
f'
Alternat
ive
l
y,
you can
fir
st convert all future dollars to today's
dollars us
in
g Equation [14.2] and then find the
PW
at i.

SECTION
14.
2 Present Worth Calculations Adjusted for
Infl
ation
TABLE
14-2
Present Worth Calculation Using an Inflated
In
tere
st
Ra
te
Year
Cost
in
n
Future
Dollars
(P
/ F,14.4%,n) PW
(1
)
(2) (3)
(4)
0 $5000
$5000
5200
0.8741 4545
2
5408
0.7641 4132
3 5624
0.6679 3757
4
5849 0.5838 3415
EXAMPLE
14.1
.
A former student
of
an engineering department wishes to donate
to
the department's
scholarship fund. Three options are available:
Plan A.
$60,000 now.
Plan
B.
$15,000 per year for 8 years beginning 1 year from
now.
Plan
C. $50,000 three years from now and another $80,000, five years from now.
From the department's perspective,
it
wants to select the plan that maximizes the
bu
y-
ing power
of
the dollars recei ved. The department head asked the engineering professor
evaluat
in
g the plans to account for inflation
in
the calculations.
If
the donation earns a
re
al
10
% per year
an
d the
infl
at
ion
rate
is
expected
to
average 3% per year, which plan
should be accepted?
Solution
The quickest evaluation method is to calculate the present worth
of
each plan
in
today's
dollars. For
pl
ans
Band
C, the easiest way to obtain the present worth
is
through the use
of
the inflated interest rate. By Equation [14.6],
if = 0.10 + 0.03 + 0.10(0.03) = 0.133
PW A = $60,000
PW
B
= $
15
,000(P/A,13.3%,
8)
= $15,000(4.7508) = $71,262
PW
c
= $50,000(P/F,13.3%,3) +
80
,
000(P/F
,
13.3
%,5)
= $50,000(0.68756) + 80,000(0.53561) = $77,227
Since
PW c
is
the largest
in
today's dollars, select plan
C.
For spreadsheet analysi
s,
the PV function
is
used to
find
PW
Band
PW c:
PV(l3
.3
%,
8, - 15000)in one ce
ll
, and PV(13.3
%,
3"
- 50000) + PV(13.3
%,
5
,,-
80000)
in
another ce
ll.
Comment
The present worths
of
plans B and C can also be found by first converting the cash flows
to today's dollars
using!
= 3%
in
Equation [14.2] and then using the real i
of
10%
in
the P / F factors. This procedure is more time-consuming, but the answers are the same.
477
Q-Solv

478
CHAP
TER
14
Effects
ofl
nfl
ation
EXAMPLE
14.2
;~';'.
Q-Solv
A
IS
-year $50,000 bond
th
at has a dividend rate o
fl
0% per year, paya
bl
e semiannually, is
currently for sale.
If
th
e expected rate
of
return of the purchaser is 8% per year, com-
pounded se
mi
annua
ll
y,
and if
th
e inflation rate is expected to be 2.5% each 6-month pe
ri
od,
what is the bond worth now
(a) without an adjustment for
infl
a
ti
on and (b) when
infl
a
ti
on
is
cons
id
ered? Perform b
ot
h hand and computer so
lu
tions.
Solution by
Hand
(a) Without inflation adjustment: The semiannual dividend is I = [(50,000)(0.
10
)]
/2
=
$2500. At a nominal 4% per 6 months for 30 periods,
th
e
PW
is
PW
=
25
00(P / A,4%
,3
0) + 5
0,
000(P / F,4%,30) = $58,645
(b) With in
fl
a
ti
on: Use
th
e
infl
ated rate if '
if = 0.
04
+ 0.025 + (0.
04
)(0.025) = 0.066 per se
mi
annual pe
ri
od
PW = 2500(P
/A,
6.6%,30) + 50,000(P/ F,6.6%,30)
= 2500( 12.9244) + 50,000(0.1470)
= $39,660
Solution by
Computer
(a) a
nd
(b) These bo
th
require simple, s
in
gle-ce
ll
func
ti
ons on a spreadsheet (Figure 1
4-2)
.
Without inflation adjusted for,
th
e
PV
function is developed
in
B2 at the nominal 4% rate
for
30 pe
ri
od
s;
with
infl
a
ti
on the rate is if = 6.6%, as determined above. See the ce
ll
tags
for
th
e formats.
X Microsoft Excel 0 I!lliIl3
(b) PWvvith
in
fl
ation
6
Ready
Figure
14-2
$
$
58,646
----I
PV(4%,30
,-
2500
,-
50000) I '
39,660
----1
PV(6.6%,30, - 2500, - 50000) I
Present
wo
rth of a bo
nd
w
ith
out a
nd
w
ith
infl
a
ti
on adjus
tm
e
nt
, Exa
mp
le
14.
2.

SECTION
14
.2
Present Worth Calculations Adjusted for Inflation
Comment
The $18,985 difference
in
PW values illustrates the tremendous negative impact made by
only 2.5% inflation each 6 months (5.06% per year). Purchasing the
$50,000 bond means
receiv
in
g $75,000
in
di
vidends over 15 years and the $50,000 principal
in
year
15
. This
is
worth o
nl
y $39,660
in
constant-value (today's) dollars.
EXAMPLE
14.3
;'.
A self-employed chemical engineer
is
on contract with Dow Chemical, current
ly
work-
in
g
in
a relatively
hi
gh-inflation country. She wishes
to
calculate a project's
PW
with
estimated costs
of
$35,000 now and $7000 per year for 5 years beginning 1 year from
now with increases
of
12
% per year thereafter for the next 8 years. Use a real interest
rate of 15% per year to make the calculations
(a) without an adjustment for inflation and
(b) cons
id
er
in
g inflation at a rate
of
11
% per year.
Solution
(a) Figure
14
-3
presents the cash
flow
s.
The PW without an adjustment for inflation
is
fo
und using i =
15
% and g = 12%
in
Equations [2.23] and [2.24] for the geo-
metric series.
PW = - 35,000 - 7000(P/A,
15
%,
4)
_ { 7000 [
1
-
(WsrJ
} (P/ F,
15
%,
4)
0.15 - 0.12
PW = ?
o 1
$35
,000
PWg = ?
2 3
4 5
0
1
=
-35,0
00 -
19
,985 - 28,247
= $- 83,232
i =
15
% per year
6 7 8
9
10
11
12
13
2 3
4
5 6 7 8 9
----
--'---'
t t
$7000 $7840
I
j
I
I
$
17
,331
12% increase
I
I~"---
per year
---I~~
Fi
gure
14-3
Cash
fl
ow diagram, Exam
pl
e 14.
3.
Year
Geometric se
ri
es year
479

480
CHAPTER
14
Effects of Inflation
In
the P / A factor, n = 4 because the $7000 cost in year
5is
dle
Al
term
in
Equa-
tion [2.23].
(b)
To
adjust for inflation, calculate the inflated interest rate by Equation [14.6].
i
f
= 0.15 + 0.
11
+ (0.15)(0.11) = 0.2765
PW = - 35,000 - 7000(P/A,27.65%,4)
_
{7000
[1
-
(#hrJ
}(P
/F,27.65%,4)
0.2765 - 0.
12
= - 35,000 - 7000(2.2545) - 30,945(0.3766)
=
$-62,436
This result demonstrates that
ill
a high-inflation economy, when negotiating the amount
of
the payments to repay a loan, it
is
economically advantageous for the borrower to
use future (inflated) dollars whenever possible
to
make the payments. The present value
of
future inflated dollars is significantly less when the inflation adjustment is included.
And
lie
hi
gher the inflation rate, the larger the discounting because the P / F and P / A
factors decrease in size.
The last two examples seem to add credence to the "buy now, pay later" phi-
lo
sophy
of
financial management. However, at some point,
th
e debt-ridden com-
pany or individual will have to
payoff
the debts and the accrued interest
wi
th
the
inflated dollars.
If
cash is not readily available, the debts cannot be repaid. This
ca
n
happen, for example, when a company unsucce
ssf
ully launches a new product,
when there
is
a serious downturn in the economy, or when an individual loses a
salary. In the longer term, this "buy now, pay later" approach must be tempered
with sound financial practices now, and in the future.
14.3
FUTURE
WORTH CALCULATIONS
ADJUSTED
FOR
INFLATION
In future worth calculations, a future amount F can have
anyone
of
four different
interpretation
s:
Case
1.
The
actual amount
of
money that will be accumulated at time n.
Case
2.
The
pur
chasing power
of
the actual amount accumulated at time n,
but stated in today's (constant-value) dollars.
Case
3.
The
number
of
future dollars requir
ed
at time n to maintain the same
purchasing power as a dollar today; that is, inflation is considered, but
in
-
terest
is
not.
Case
4.
The
number
of
dollars required at time n to maintain
pur
chasing
po
wer
and
ea
rn
a stated real interest rate.

SECTION 14.3 Future Worth Calculations Adjusted for Inflation
Depending upon which interpretation is intended, the F value
is
calculated
dif
-
ferently,
as
described below. Each case is illustrated.
Case 1:
ActualAmount
Accumulated
It should be clear that
F,
the actual amount
of
money accumulated, is obtained using the inflation-adjusted (market) interest
rate.
F = P(1 + 9" =
P(F
/
P,if,n)
[14.7]
For example, when we are quoted a market rate
of
10%, the inflation rate is in-
cluded.
Over a 7-year period, $1000 will accumulate to
F = 1000(F/P,10%,7) = $1948
Case
2:
Constant-Value with
Purchasing
Power The purchasing power
of
future dollars is determined by first using the market rate
if
to calculate F and
then deflating the future amount through division by
(1
+ f)fl.
_ P(1 + 9" _
P(F
/
P,i"n)
F - (1 +
f)"
-
(1
+
f)"
[14.8]
This relation, in effect, recognizes the fact that inflated prices mean $1 in the fu-
ture purchases less than
$1
now. The percentage loss in purchasing power is a
measure
of
how much less. As an illustration, consider the same $1000 now, a
10% per year market rate, and an inflation rate
of
4% per year. In 7 years, the pur-
chasing power has risen, but only to $1481.
F = 1000(F/P,10%,7) = $1948
=$1
481
(1.04?
1.3159
This
is
$467 (or 24%) less than the $1948 actually accumulated at 10% (case 1).
Therefore, we conclude that 4% inflation over 7 years reduces the purchasing
power
of
money
by
24%.
Also for case 2, the future amount
of
money accumulated with today's buying
power could equivalently be determined by calculating the real interest rate and
using it
in
the F / P factor to compensate for the decreased purchasing power
of
the dollar. This real interest rate
is
the i in Equation [14.6].
if = i + f +
if
= i(1 +
f)
+ f
. i
f
-
f
l = 1 + f
[14.9]
The real interest rate
i represents the rate at which today's dollars expand with their
same purchasing
power
into equivalent future dollars. An inflation rate larger than
the market interest rate leads to a negative real interest rate. The use
of
this inter-
est rate
is
appropriate for calculating the future worth
of
an investment (such as a
savings account or money market fund) when the effect
of
inflation must be re-
moved. For the example
of
$1000 in today's dollars from Equation [14.9]
0.10 - 0.04
i = = 0.0577, or 5.77%
1
+ 0.04
F = 1000(F/P,5.77%,7) = $1481
481

482
SettingMARR
CHAPTER
14
Effects
of
Inflation
The market interest rate
of
10% per year has been reduced to a real rate that is
less than 6% per year because
of
the erosive effects
of
inflation.
Case
3:
Future
Amount
Required, No Interest This case recognizes that prices
increase when inflation is present. Simply put, future dollars are worth less, so
more are needed. No interest rate is considered at all in this case. This is the situ-
ation present
if
someone asks, How much will a car cost
in
5 years
if
its current
cost is
$20,000 and its price will increase by 6% per year? (The answer is
$26,765.)
No
interest rate, only inflation, is involved. To find the future cost, sub-
stitute
ffor
the interest rate in the F / P factor.
F =
P(l
+
f)"
= P(F /P,J,n)
[14.10]
Reconsider the $1000 used previously.
If
it is escalating at exactly the inflation
rate
of
4% per year, the amount 7 years from now will be
F = 1000(F/P,4%,7) = $1316
Case
4:
Inflation
and
Real Interest This
is
the case applied when a MARR is
established. Maintaining purchasing power and earning interest must account for
both increasing prices (case 3) and the time value
of
money.
If
the growth
of
capital is to keep up, funds must grow at a rate equal to or above the real interest
rate
i plus a rate equal to the inflation rate f Thus, to make a real rate
of
return of
5.77
% when the inflation rate is 4%, if is the market (inflation-adjusted) rate that
must be used. For the same
$1000 amount,
if = 0.0577 + 0.04 + 0.0577(0.04) = 0.10
F = 1000(F / P,10%,7) = $1948
This calculation shows that $1948 seven years in the future will be equivalent
to
$1000 now with a real return
of
i = 5.77% per year and inflation
off
= 4% per
year.
Table
14-3
summarizes which rate is used in the equivalence formulas for
the different interpretations
of
F.
The calculations made in this section reveal
that
$1000 now at a market rate
of
10% per year would accumulate to $1948 in
7 years; the $1948 would have the purchasing power
of
$1481
of
today's dollars
iff
= 4% per year; an item with a cost
of
$1000 now would cost $1316 in 7 years
at an inflation rate
of
4% per year; and it would take $1948
of
future dollars to be
equivalent to the
$1000 now at a real interest rate
of
5.77% with inflation con-
sidered at 4%.
Most corporations evaluate alternatives at a MARR large enough to cover
inflation plus some return greater than their cost
of
capital, and significantly
higher than the safe investment return
of
approximately 3.5% mentioned earlier.
Therefore, for case 4, the resulting MARR will normally be higher than the ma
r-
ket rate if ' Define the symbol
MARR
f
as the inflation-adjusted MARR, which is
calculated in a fashion similar to
if '
MARR
f
= i + f +
i(f)
[14.11]

SECTION 14.3 Future Worth Calculations Adjusted for Inflation
TABLE
14-3
Calculation Methods for Various Future Worth Interpretations
Future
W
or
th
Desired
Case I: Actual dollars
accumulated
Case 2: Purchasing power
of
accumulated dollars
in
terms
of
today's
dollars
Case 3: Dollars required
for same purchasing
power
Case 4: Future dollars to
maintain purchasing
power and to earn a
return
Method
of
Calcu
lat
i
on
Use stated market
rate
ij'in equivalen
ce
fo
rm
ul
as
Use market rate
if
in
equivalence and
divide by
(I
+
f)"
or
Use
real i
Usefin
place
of
i in
equivalence
formulas
Calculate
if and use in
equivalence
formulas
Example
for
P =
$1000
, n = 7,
i
f
=
10%
,
f=
4%
F = 1000(F/P,10%,7)
F =
_lO_O_O('-.F:.-/
P-,,-=lO_o/t...:.o,
7-"-)
(1.04/
or
F = 1000(F/P,5.77%,7)
F = 1000(F / P,4%,
7)
F = 1000(F/P,1O%,7)
The real rate
of
return i used here is the required rate for the corporation relative
to its cost
of
capital.
Now
the future worth F,
or
FW, is calculated as
F = P(1 +
MARRl
' =
P(F
/
P,MARR
f,
n)
[14.12]
For
example, if a company has a WACC (weighted average cost
of
capital)
of
10% per year and requires that a project return 3% per year above its WACC, the
real return
is
i =
13
%. The inflation-adjusted
MARR
is calculated by including
the inflation rate
of
, say, 4%
per
year. Then, the project PW, A
W,
or
FW
will
be
determined at the rate obtained from Equation [14.11].
MARR
j
= 0.
13
+ 0.
04
+ 0.13(0.04) =
17
.52%
A similar computation can be made for an individual using
i as the expected
real rate that
is
above the safe investment rate. When an individual is satisfied with
a required real return equal to a safe investment rate, approximately
i = 3.5%,
or
a corporation
is
satisfied with a real return equal to a safe investment rate,
Equa
-
tions [14.
11]
and [14.6] have the same result; that is, MARRr =
if'
for the corpo-
ration
or
the individual.
Abbott Mining Systems wants to determine whether
it
should
"buy"
now
or
"buy"
later
for upgrading a piece
of
equipment used in deep mining operations
in
one
of
its inter-
national operations.
If
the company selects plan
A,
the equipment w
il
l be purchased
now for
$200,000. However,
if
the company selects plan I, the purchase will be deferred
483
(
Chap]
10
t
/
0
[
WACC

484
CHAPTER 14 Effects
of
Inflation
for 3 years when the cost is expected to rise rapidly to
$340,000. Abbott is ambitious;
it
expects a real MARR
of
12% per year. The inflation rate
in
the country has averaged
6.75% per year. From only an economic perspective, determine whether the company
shou
ld
purchase now or later (a) when inflation
is
not considered and (b) when inflation
is considered.
Solution
(a) Inflation not considered: The real rate, or MARR, is i =
12
% per year. The cost
of
plan I
is
$340,000 three years hence. Calculate the FW value for plan A three
years from now and select the lower cost.
FW
A =
-200
,000(F / P,
12
%,
3)
=
$-280
,986
FW,
=
$-340,000
Select plan A (purchase now).
(b) Inflation considered: This
is
case
4;
there
is
a real rate (12%), and inflation
of
6.75% must be accounted
for.
First, compute the inflation-adjusted MARR
by
Equation [14.11].
i
f
= 0.12 + 0.0675 + 0.12(0.0675) = 0.1956
Use if to compute the FW
va
lu
e for plan A in future dollars.
FW
A
= -200,000(F/P,19.56%,3) =
$-341,812
FW, =
$-340,000
Purchase later (pl
an
I)
is
now selected, because
it
requires fewer equivalent
future dollars.
The
inflation rate
of
6.75% per year has raised the equivalent
future worth
of
costs
by
21.6%
to
$34 J
,8
12.
This is the same
as
an
increase
of
6.75% per year, compounded over 3 years, or (1.0675)3 - J = 21.6
%.
Most countries have inflation rates in the range
of
2% to 8% per year, but hy-
perinflation
is a problem in countries where political instability, overspending
by the government, weak international trade balances, etc., are present. Hyper-
inflation rates may be very
high-10
% to 100%
per
month. In these cases, the
government may take drastic actions: redefine the
CUlTency
in terms
of
the cur-
rency
of
another country, control banks and corporations, and control
th
e flow
of
capital into and out
of
the country in order to decrease inflation.
In a hyperinflated environment, people usually spend all their money immedi-
ately since the cost will be so much higher the next month, week, or day. To ap-
preciate the disastrous effect
of
hyperinflation on a company's ability
to
keep up,
we can rework Example
14.4b using an inflation rate
of
10%
per
month, that is, a
nominal
120% per year (not considering the compounding
of
inflation). The
FW
A
amount skyrockets and plan I is a clear choice.
Of
course, in such an environment
the
$340,000 purchase price for plan I three years hence would obviously not be
guaranteed, so the entire economic analysis is unreliable. Good econolnic
decisions
in
a hyperinflated economy are very difficult to make using traditional
engineering economy methods, since the estimated future
va
lues are totally
unreliable and the future availability
of
capital is uncertain.
