Blank L., Tarquin A. Engineering Economy (McGraw-Hill Series in Industrial Engineering and Management)
Подождите немного. Документ загружается.


SECTION 16.2 Straight Line (SL) Depreciation
balance for tax
or
book purposes.
Because
of
the continuing importance
of
the
SL
and
DB
methods, they are explained in the
next
two sections
prior
to
MACRS.
Tax law revisions
occur
often,
and
depreciation rules are
changed
from time to
time in the
United States and
other
countries.
For
example,
in 2003 and 2004, a
special depreciation
allowance
of
either
30%
or
50%
of
a new
asset's
first
cost
could
be
taken in its initial
year
in
service.
That
was in addition to the Section 179
Deduction.
This
was an
effort
to
promote
capital investment. Although the tax
rates and depreciation guidelines
at
the time you read this material
may
be
slightly
different, the general principles and equations are applicable to all
U.S.
corpora
-
tions.
For
more depreciation
and
tax law information,
consult
the U.S.
Department
of
the Treasury, Internal
Revenue
Service (IRS), website at www.irs.gov. Perti-
nent publications can
be
downloaded
via
Acrobat
Reader. Publication 946,
How
to
Depreciate
Property, is especially applicable to this chapter.
MACRS
and most
corporate tax depreciation laws are discussed in it.
16.2
STRAIGHT LINE
(SL)
DEPRECIATION
Straight line depreciation derives its
name
from the fact that the
book
value de-
creases linearly with time.
The
depreciation rate d =
lin
is
the
same
each
year
of
the recovery period n.
Straight line
is
considered the standard against which any depreciation model
is compared.
For
book depreciation purposes,
it
offers an excellent representa-
tion
of
book
value for any asset that is used regularly
over
an estimated
number
of
years.
For
tax depreciation, as mentioned earlier, it is not used directly in the
United States, but it
is
commonly
used in
most
countries for tax purposes. However,
the
U.S.
MACRS
method includes a version
of
SL
depreciation with a larger n
value than that allowed by regular
MACRS
(see Section 16.5).
The
annual
SL
depreciation is determined by multiplying the first
cost
minus
the salvage value by
d.
In equation form,
D/
=
(B
- S)d
B-S
n
where t =
year
(t =
I,
2,
...
, n)
D, = annual depreciation
charge
B = first
cost
or
unadjusted basis
S = estimated salvage value
n = recovery period
d = depreciation rate = 1
In
[16.1]
Since the asset
is
depreciated by the
same
amount
each year, the
book
value after
t years
of
service, denoted by
BY"
will
be
equal to the first
cost
B minus the an-
nual depreciation times
t.
[16.2]
Earlier
we
defined
d,
as a depreciation rate
for
a specific
year
t.
However, the
SL
model has the
same
rate for all years, that is,
d = d =
1..
[16.3]
t n
"
::>
~
..:.:
o
o
ill
535
B
S
-------1
Time
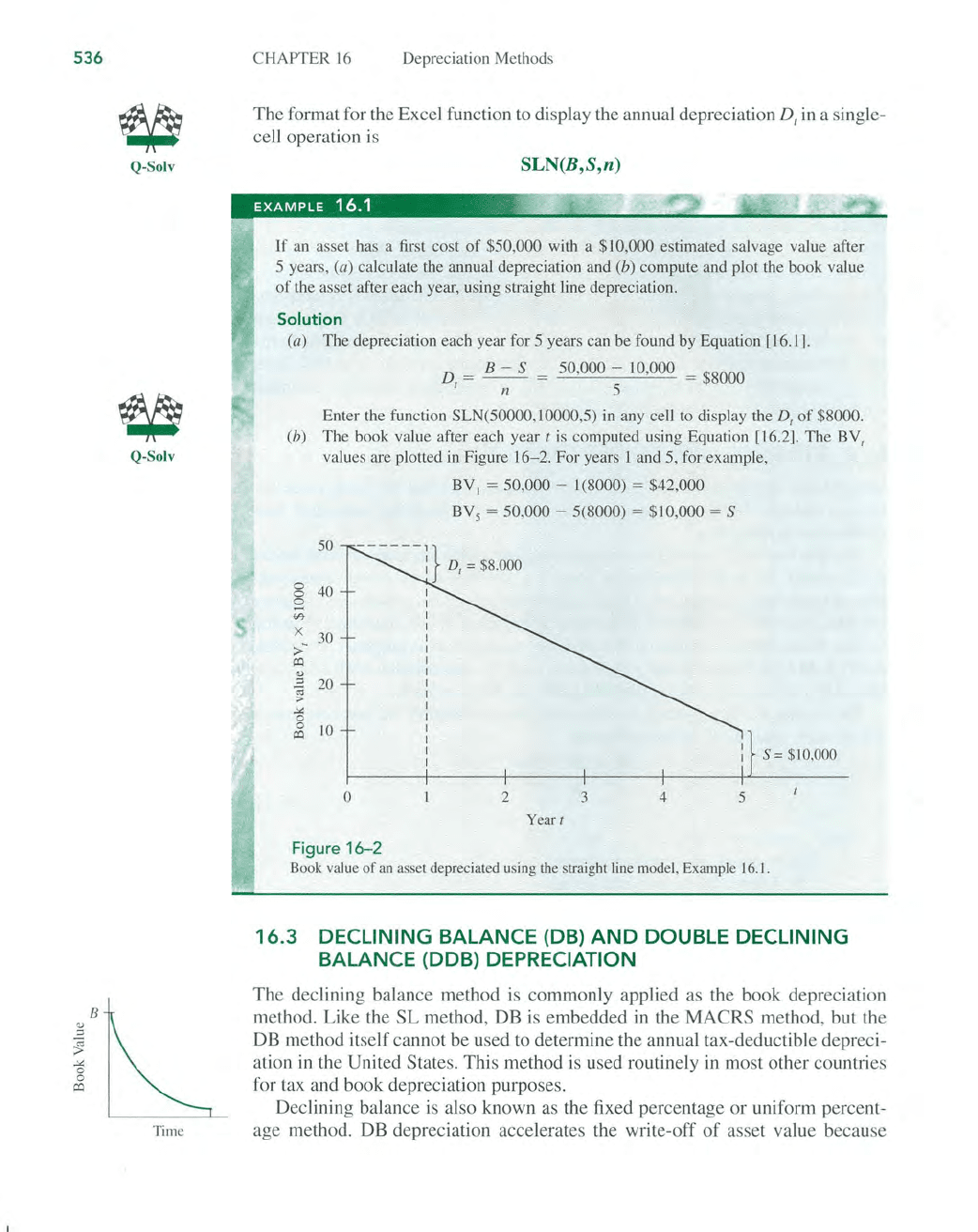
536
Q-Solv
Q-So
lv
B
Time
CHAPTER
16
Depreciation Methods
The
format for the Excel function to display the annual depreciation D,
in
a single-
cell operation is
SLN(B
,S,n)
EXAMPLE 16.1 '
If
an
asset has a first cost
of
$50,000 with a $10,000 estimated salvage value after
5 years,
(a) calculate the annual depreciation and (b) compute and plot the book
va
lue
of
the asset after each year, using straight line depreciation.
Solution
(a) The depreciation each year for 5 years can be found by Equation [16.
I]
.
D = B - S = 50,000 -
10
,000 = $8000
'n
5
Enter the function
SLN(50000,10000,5)
in
any cell to display the
D,
of
$8000.
(b) The book value after each year t is computed using Equation [16.2]. The BY,
values are plotted
in
Figure
16-2
. For years 1 and 5, for example,
BY
,
= 50,000 - [(8000) = $42,000
BY
s
= 50,000 - 5(8000) = $10,000 = S
50
0
40
0
S
'"
x
>-
30
o:!
(!)
::s
20
-;;;
>
-"
0
0
10
o:!
s=
$
10
,000
o
2
3
4
5
Yeart
Fi
gure
16- 2
Book value
of
an asset depreciated using the straight line model, Example
16
.
1.
16
.3 DECLINING BALANCE (DB)
AND
DOUBLE DECLINING
BALANCE (DDB) DEPRECIATION
The
declining balance method is commonly applied as the book depreciation
method. Like the
SL
method,
DB
is embedded in the
MACRS
method,
but
the
DB method itself
cannot
be used to determine the annual tax-deductible depreci-
ation
in
the United States. This method is used routinely in most other countries
for tax and book depreciation purposes.
Declining balance
is
also
known
as the fixed percentage
or
uniform percent-
age method. DB depreciation accelerates the write-off
of
asset value because

SECTrON
16.
3 Declining Balance and Double Declining Balance Depreciation
the annual depreciation is determined by multiplying the book value
at
the be-
ginning
ofa
year
by a fixed (uniform) percentage d, expressed in decimal form.
If
d = 0.1, then 10%
of
the book value
is
removed each year. Therefore, the de-
preciation amount decreases each year.
The
maximum annual depreciation rate for the DB method is twice the straight
line rate, that is,
d
max
= 2/ n [16.4]
In this case the method
is
called double declining balance (DDB).
If
n =
10
years, the DDB rate is
2/
to = 0.2; so 20%
of
the
book
value is removed an-
nually. Another commonly used percentage for the DB method is
150%
of
the
SL
rate, where d = l.5/ n.
The depreciation for year t
is
the fixed rate d times the book value at the end
of
the previous year.
D
t
= (d )
BV
t
_
1
The actual depreciation rate for each year
t,
relative to the first cost B, is
d,
=
d(1
-
dy
- I
[16.5]
[16.6]
If
B
V,
_I
is
not known, the depreciation in year f can be calculated using
Band
d,
from Equation [16.6].
[ 16.7]
Book
value
in
year t is determined
in
one
of
two ways: by using the rate d and
first cost
B,
or
by subtracting the current depreciation charge from the previous
book
value.
The
equations are
BV
t
= B(l - d )t
BV
/ =
BV
t
-
I
-
D
t
[16.8]
[16.9]
It
is
important to understand that the book value for the DB method never goes
to zero, because the book value is always decreased by a fixed percentage.
The
implied salvage value after n years
is
the BV
II
amount, that is,
Implied salvage value
=
impliedS
= BV
n
= B(1 -
d)"
[16.tO]
If
a salvage value is estimated for the asset, this estimated S value
is
not
Llsed
in the DB
or
DDB
method to calculate annual depreciation. However,
if
the im-
plied
S < estimated S, it
is
correct to stop charging further depreciation when the
book value is at
or
below the estimated salvage value. In most cases, the esti-
mated
S
is
in
the range
of
zero to the implied S value. (This guideline is important
when the DB method can be used directly for tax depreciation purposes.)
If
the fixed percentage d is not stated, it
is
possible to determine an implied
fixed rate using the estimated
S value,
if
S > O.
The
range for d is 0 < d < 2/
n.
Implied d = 1 _ ( ! ) I/
Il
[16.11]
~
The Excel functions
DDB
and DB are used to display depreciation amounts for
ISl
specific years (or any other unit
of
time).
The
function is repeated in consecutive E-Solve
537

538
DB
andDDB
functions
CHAPTER
16
Depreciation Methods
spreadsheet cells because the depreciation amount
D,
changes with
t.
For the dou-
ble declining balance method the format is
DDB
(B,S,n,t,d)
The entry d is the fixed rate expressed as a number between 1 and 2.
If
omitted,
this optional entry is assumed to be 2 for DDB. An entry
of
d = 1.5 makes the
/ DDB function display
150% declining balance method amounts. The DDB func-
'------,------"
I tion automatically checks to determine when the book value equals the estimated
t S value. No further depreciation
is
charged when this occurs. (In order to allow
(
AfP.
J
full
depreciation charges to be made, ensure that the S entered is between zero
and the implied
S from Equation [16.10].) Note that d = 1 is the same as the
straight line rate
l/n,
but D, will
not
be the
SL
amount
because declining balance
depreciation is determined
as
a fixed percentage
of
the previous year's book
value, which is completely different from the
SL
calculation in Equation [16.1].
Q-Solv
The DB function must be used carefully. Its format is DB(B,S,n,t). The fixed
rate
d
is
not entered in the DB function; d is an embedded calculation using a
spreadsheet equivalent
of
Equation [16.11]. Also, only three significant digits are
maintained for
d,
so the book value may go below the estimated salvage value
due to round-off errors. Therefore,
if
the depreciation rate is known, always use
the
DDB
function to ensure correct results. The next two examples illustrate DB
and DDB depreciation and these spreadsheet functions.
EXAMPLE
16.2
A fiber optics testing device is to be DDB depreciated. It has a first cost of $25,000 and
an
estimated salvage
of
$2500 after 12 years. (a) Calculate the depreciation and book
value for years 1 and 4. Write the Excel functions to display depreciation for years 1 and
4. (b) Calculate the implied salvage value after 12 years.
Solution
(a) The DDB fixed depreciation rate
is
d = 21n =
2/12
= 0.1667 per year. Use
Equations [16.7] and [16.8].
Year
1:
DI = (0.1667)(25,000)(1 - 0.1667)1 - 1 = $4167
BV
1
= 25,000(1 - 0.1667)1 = $20,833
Year
4:
D4
= (0.1667)(25,000)(1 - 0.1667)4-1 = $2411
BV
4
=
25
,000(1 - 0.1667)4 = $12,054
The DDB functions for
DI and
D4
are, respectively, DOB(25000,2500,
12
,
1)
and
00B(25000
,2500,12,4).
(b) From Equation [16.10], the implied salvage value after
12
years is
Implied
S =
25
,000(1 - 0.1667)12 = $2803
Since the estimated
S = $2500 is less than $2803, the asset
is
not fully depreci-
ated when its 12-year expected life is reached.

SECTION
16.
3 Declining Balance and Double Declining Balance Depreciation
EXAM
PL
E 16.3 .
Freeport-McMoRan Mining Company has purchased a computer-controlled gold ore grad-
ing unit for
$80,000. The unit has
an
anticipated life
of
10 years and a salvage value
of
$10,000. Use the
DB
and DDB methods
to
compare the schedule
of
depreciation and book
values for each year.
Solve
by
hand and
by
computer.
Solution by Hand
An
implied
DB
depreciation rale
is
determined
by
Equation [16.11].
d = I _ (
10
,000
)1
/
10
= 0.1877
80,000
Note that 0.1877 < 2/ n = 0.2, so this DB model does not exceed twice the straight !lne
rate. Table
16
- 1 presents the D{ values using Equation [16.5] and the
BY{
values from
Equation [16.9] rounded
to
the nearest dollar. For example,
in
year t = 2, the DB results are
D2
=
ci(BY
I
)
= 0.1877(64,984) = $12,
197
BY
2 = 64,984 - 12,197 = $52,787
Because we round off to even dollars, $2312
is
calculated for depreciation in year
10,
but
$2318
is
deducted
to
make
BY
IO
= S = $10,000 exactly. Similar calculations for DDB
with
d = 0.2 result
in
the depreciation and book value series
in
Table 16-1.
TABLE 16-1 D{ and BV{
Val
ues for
DB
and DDB Depreciation.
Example 16.3
Declining Balance Double Declining
Year
t D
t
BV
t
D
t
BV
t
0
$80,000
$80,000
1
$15,016 64,984 $16,000 64,000
2
12
,
197
52,787
12
,800
51
,200
3
9,908 42,879
10
,240 40,960
4 8,048 34,831 8,192 32,768
5
6,538 28,293 6,554
26,214
6
5,
311
22,982 5,243 20,972
7 4,314 18,668
4,194
16,777
8
3,504 15,164 3,355
13,422
9
2,846
12,318
2,684
10,737
10
2,318 10,000 737
10,000
Solution by Computer
The spreadsheet
in
Figure
16
- 3 displays the results for the DB and DDB methods.
Thexy
~
scatter chart plots book values for each year. Since the fixed rates are
close-O.1877
for DB
~
and 0.2 for DDB- the annual depreciation and book value series are approximately equal E·Solve
for
the two methods.
539

540
CHAPTER 16
Depreciation Methods
X M,crosoft Excel
!!Ira
Ei
JZZ
_ D X
A
1
2
First
co
st 80,000
3
Sa
lv
age
10,000
4
Reco
very
pd
.
10
5
6
Oeclininq
balan
ce
$80,000
7 Year, I
01
DB
book
va
lu
e
$70,000
8
1
$ 15,016 $ 64
,98
4 $
..
$&0,000
9
2
$ 12,197 $ 52,787 $
:;
$50,000
10
3
$ 9,908 $ 42,878 $
..
$4
0,
000
.
11
4 $ 8,048 $
34
,830
$
..
$30
,0
00
0
12
5
$ 6,538
$
28
,29
3 $
0
$2
0,000
"
lY
6
$
5,31
1 $ 22,982 $
$ 10,000
'\
"-
'"
'"
14
7 $ 4
,31
4 $ 18
,668
$
$-
15
8
$ 3,
50
4 $ 15,164 $
16
9
$ 2,846 $
12
,
318
$
17
10
$ 2,312 $ 10,006 $
18
19
'20
21
= DDB(B$2,B$3,B$4, I 0, 1
_877)
2
I~
~
~
~I
Sheet!
-Sheet2
Sheet3
Sheet4
Ready
Figure
16-3
Spreadsheel solution for annual depreciation and book values for DB and
DDB
depreciation,
Example
16
.3_
Comment
Note
in
the cell tags that the DDB function is used
in
both columns
Band
D to determine an-
nual depreciation.
The
DDB function for the declining balance method has the d rate entered
asl
,877. This
is
done for accuracy. As mentioned earlier, the DB function automatically cal-
culates the implied rate by Equation [16.l1] and maintains it to only three significant di
gi
ts.
Therefore,
if
the
DB
function were used
in
column B (Figure
16-3)
, the fixed rate applied
would be 0.188.
The
resulting Dr and BV! values for years 8, 9, and 10 would be as follow
s:
t
8
9
10
$3,501
2,842
2,308
$15,120
12,277
9,969
Also noteworthy is the fact that the DB function uses the implied rate without a check to
halt the book value at the estimated salvage value. Thus,
BV
10
will go slightly below
S
= $10,000, as shown above. However, the DDB function uses a relation different from
that
of
the DB function to determine annual
depreciation-one
that correctly stops depre-
ciating at the estimated salvage value, as shown in Figure
16
-3,
cell E17.

SECTION 16.4 Modified Accelerated Cost Recovery System (MACRS)
16.4
MODIFIED
ACCELERATED COST RECOVERY
SYSTEM (MACRS)
In the 1980s, the U.S. introduced MACRS as the required tax depreciation
method for
all depreciable assets. Through
MACRS,
the 1986 Tax Reform Act
defined statutory depreciation rates that take advantage
of
the accelerated DB
and
DDB
methods. Corporations are free to apply any
of
the classical methods
for book depreciation.
Many aspects
of
MACRS
deal with the specific depreciation accounting as-
pects
of
tax law. This chapter covers only the elements that materially affect
after-tax economic analysis. Additional information on how the
DDB
, DB, and
SL
methods a
re
embedded into
MACRS
and how to derive the
MACRS
depre-
ciation rates is presented and illustrated in the chapter appendix, Sections 16A.2
and 16A
.3
.
MACRS determines annual depreciation amounts using the relation
[16.12]
where the depreciation rate
d,
is
provided
in
tabulated form. As for other meth-
ods, the book value
in
year t is determined by subtracting the depreciation
amount from the previous
year's
book value,
[16.13]
or
by subtract
in
g the total depreciation from the first cost.
BV
t
= first cost - sum
of
accumulated depreciation
j=t
= B - I
_P
i
[16.14]
j=1
The first cost B is always completely depreciated, since
MACRS
assumes that
S = 0, even though there may be a positive salvage that is realizable.
The MACRS recove
ry
periods are standardized to the values
of
3,5
, 7, 10,
15
,
and
20
years for personal property.
The
real property recovery period for struc-
tures is commonly 39 years, but it is possible to justify a 27.5-year recovery for
residential rental property. Section 16.5 explains how to determine an allowable
MACRS recovery period. The
MACRS
personal property depreciation rates
(d,
values) for n =
3,5,7,
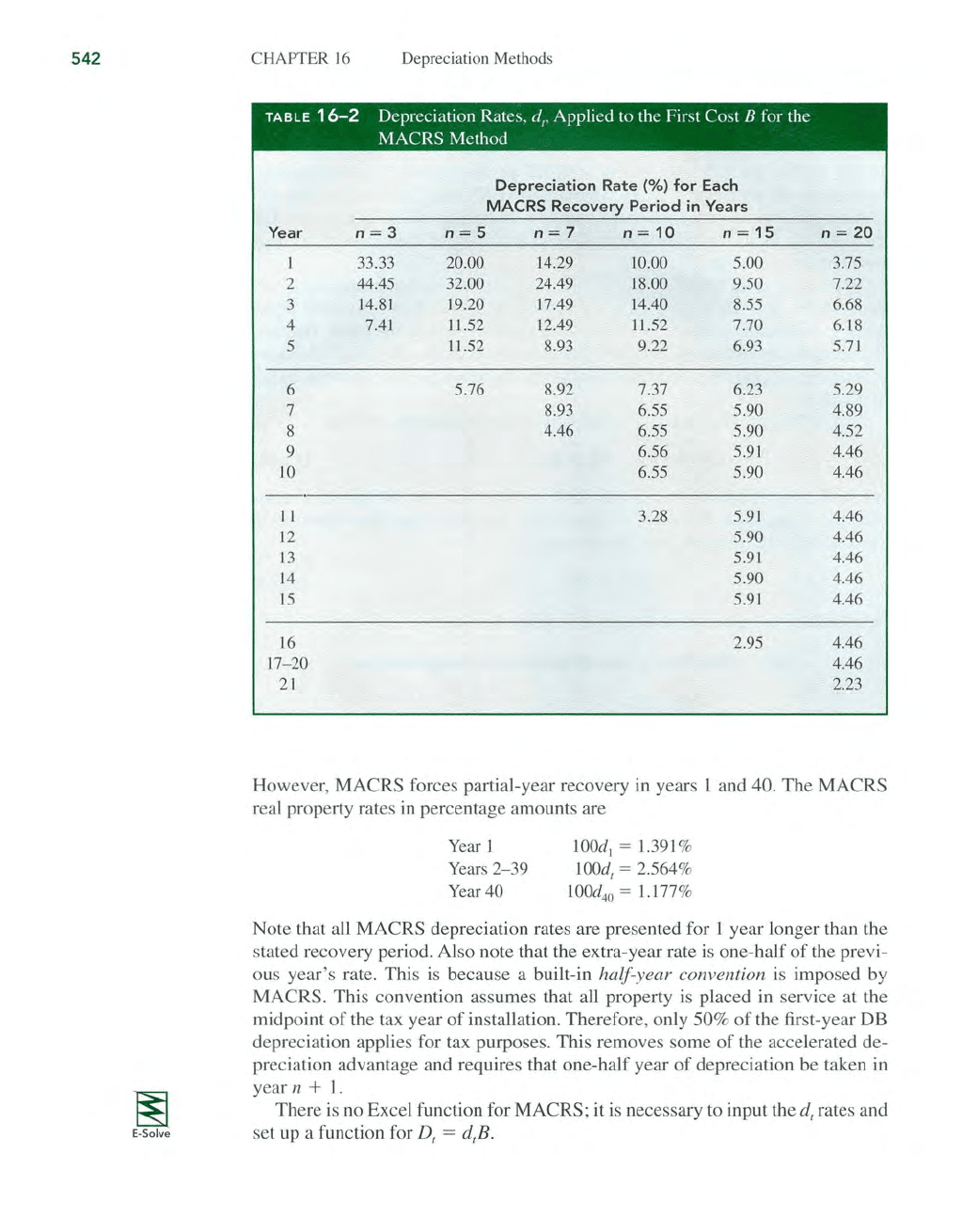
10, IS, and 20 for use in Equation [16.12] are included
in
Table 16
-2.
(These values are used often throughout the remainder
of
this text,
so you may wish to tab this page.)
MACRS
depreciation rates incorporate the DDB method
Cd
= 2/ n) and
switch to
SL
depreciation during the recovery period as an inherent compo-
nent for person.al prope
rt
y depreciation.
The
MACRS
rates start with the
DDB rate
or
the 150% DB rate and switch when the
SL
method offers faster
write-off.
For real property, MACRS utilizes the
SL
method for n = 39 throughout the
recovery period. The annual percentage depreciation rate is
d =
1/39
= 0.02564.
541
542
~
E-Solve
CHAPTER
16
Depreciation Methods
T
AB
LE
16
- 2 Depreciation Rates, d
t'
Applied
to
the First Cost B
for
the
MACRS Method
Depreciat
ion
Rate
(%) for Each
MACRS
Recove
ry
Period
in
Y
ears
Ye
ar
n = 3
n=5
n = 7
n =
10
n =
15
33.33 20.00 14.29
10.00 5.00
2 44.45 32.00 24.49 18.00 9.50
3
14
.81 19.20 17.49 14.40 8.55
4 7.41 11.52 12.49 11.52
7.70
5
11.52 8.93 9.22 6.93
6
5.76 8.92 7.37 6.23
7 8.93 6.
55
5.90
8
4.46
6.55
5.90
9
6.56 5.91
10
6.
55
5.90
II
3.28
5.91
12
5.90
13
5.
91
14
5.90
J5
5.
91
16
2.95
17
- 20
21
n =
20
3.75
7.22
6.68
6.18
5.7J
5.29
4.89
4.52
4.46
4.46
4.46
4.46
4.46
4.46
4.46
4.46
4.46
2.23
However, MACRS forces partial-year recovery in years 1 and 40. The MACRS
real property rates in percentage amounts are
Year I
Years
2-39
Year
40
100d
i
= 1.391 %
IOOd
t
= 2.
564
%
100d
4o
= 1.177%
Note that all MACRS depreciation rates are presented for 1 year longer than the
stated recovery period. Also note that the extra-year rate is one-half
of
the previ-
ous year's rate. This is because a built-in
half
-
year
convention is imposed by
MACRS. This convention assumes that all property is placed
in
service at the
midpoint
of
the tax year
of
installation. Therefore, only 50%
of
the first-year DB
depreciation applies for tax purposes. This removes some
of
the accelerated de-
preciation advantage and requires that one-half year
of
depreciation be taken
in
year n + I.
There
is
no Excel function for MACRS; it is necessary to input the d
t
rates and
set up a function for
D
t
= dtB.

SECTION 16.4 Modified Accelerated Cost Recovery System (MACRS)
EXAMPLE
16.4
~~
Baseline, a nationwide franchise for environmental engineering services, bas acquired new
workstations and 3D modeling software for its
100 affiliate sites at a cost
of
$4000 per site.
The estimated salvage for each system after 3 years is expected to be 5%
of
the first cost.
The franchise manager
in
the home office in San Francisco wants to compare the depreci-
ation for a 3-year MACRS model (tax depreciation) with that for a 3-year DDB model
(book depreciation). He is especially curious about the depreciation over tbe next 2 years.
Using hand and computer solution,
(a) Determine which model offers the larger total depreciation after 2 years.
(b) Detemline the book value for each model after 2 years and at the end
of
the recov-
ery period.
Solution by Hand
The basis
is
B = $400,000, and the estimated S = 0.05(400,000) = $20,000. The MACRS
rates for
n = 3 are taken from Table
16-2,
and the depreciation rate for DDB
is
d
max
=
2/3
= 0.6667. Table
16
-3
presents the depreciation and book values. Year 3 depreciation for
DDB would be $44,444(0.6667)
= $29,629, except that this would make BV
3
< $20,000.
Only
the remaining amount
of
$24,444
is
removed.
(a) The 2-year accumulated depreciation values from Table 16-3 are
MACRS:
DDB:
D
J
+ D2 = $133,320 + 177,800 = $311,120
D
J
+ D
z
= $266,667 + 88,889 = $355,556
The DDB depreciation is larger. (Remember that for tax purposes, Baseline does not
have the choice
in
the United States
of
the DDB model
as
applied here.)
(b) After 2 years the book value for DDB at $44,444 is 50%
of
the MACRS book value
of
$88,880. At the end
of
recovery (4 years for MACRS due to the built-in half-year
convention, and 3
yeaTS
for DDB), the MACRS book value is BV
4
= 0 and for
DDB, BY
3 = $20,000. This occurs because MACRS always removes the entire first
cost, regardless
of
the estimated salvage value. This is a tax depreciation advantage
of
the MACRS method (unless the asset is disposed
of
for more than the MACRS-
depreciated book value, as discussed
in
Section 17.4).
TABLE
16-3
Comparing MACRS and DDB Depreciation, Example 16.4
MACRS DDB
Tax
Book Book
Book
Year Rate Depreciation Value Depreciation Value
0 $400,000 $400,000
0.3333
$133,320 266,680
$266,667 133,333
2
0.4445 177,800
88
,880 88,889
44,444
3
0.1481 59,240
29,640
24,444 20,000
4 0.0741 29,640
0
543

544
CHAPTER
16
Depreciation Methods
"'"
Micro
soft Excel
1!!Ir;]
f3
ij
Example164
1!!I~f3
17
1
2
3
4
Figure
16-4
MACRS
Rate
Depreciation
0.3333
0.4445
o
14
81
0.
0741
10000
DDS
Sookvalue
Depreciation Sook value
$266,680 $266,667 $133,333
$88,880 $88,889
$44.444
$29,640
$24.4441
$20,000
-----..r-1
F6-
E7
1
$0
= DDB(B
$l
,
F$1
,3
,A 7)
Comparison
of
MACRS
and DDB depreciation methods using a spreadsheet, Example 16.4.
Solution by
Computer
Figure
16-4
presents the spreadsheet solution using the DDB function, in column E,
th
e
MACRS rates
in
column B, and Equation [16.12]
in
column C.
(a)
The
2-year accumulated depreciation values are
MACRS
, add cells
C6
+ C7:
DDB, add cells
£6
+ E7:
(b) Book values after 2 years are
MACRS, cell D7:
DDB, cell F7:
$133,320
+ 177,800 = $311,120
$266,667
+ 88,889 = $355,556
$88,880
$44,444
The
book values at the end
of
the recovery periods are
in
cells
D9
and F8.
Comment
It
is advised to set up a spreadsheet template for use with depreciation problems
in
this and
future chapters.
The
format and functions
of
Figure
16-4
are a good template for MACRS
and
DDB
methods.
