Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

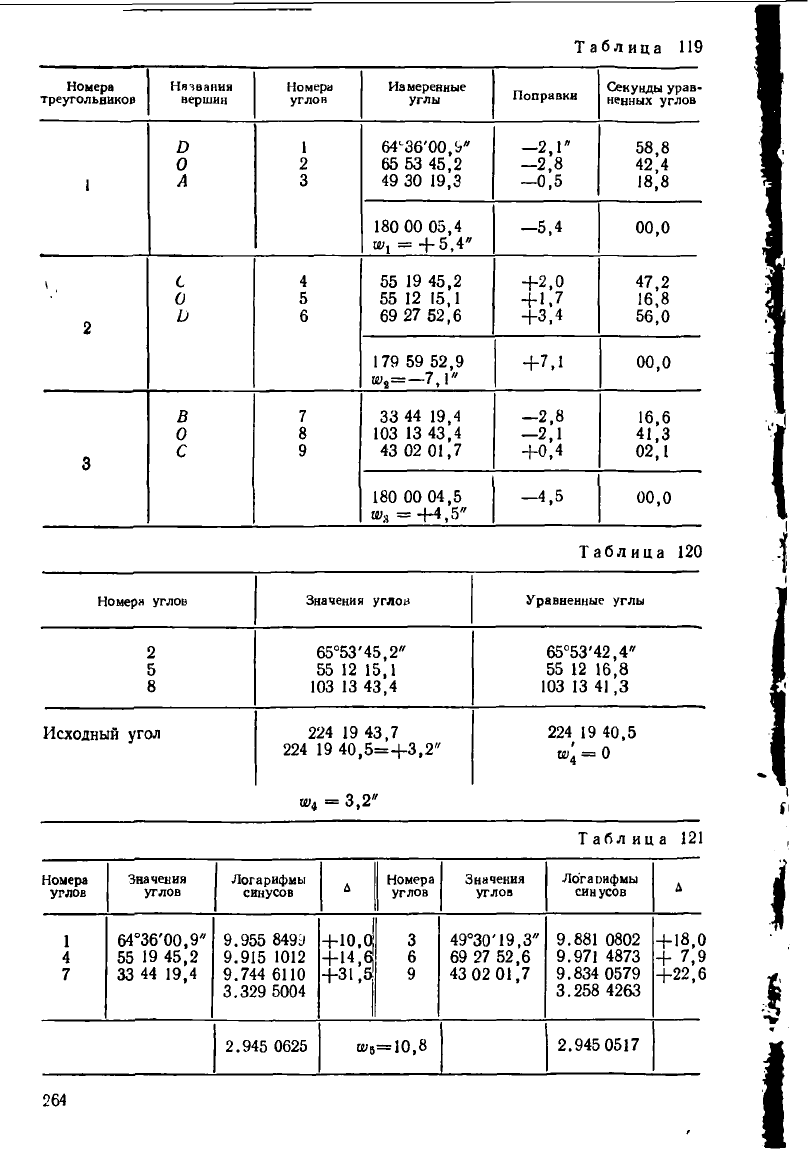
Таблица 118

Номера

треугольников

Начвання

вершин

Номера

углов

Измеренные

углы

Поправки

Секунды урав-

ненных углов

64^36'ОО.Ь"

65 53 45,2

49 30 19,3

—2,1"

-2,8

-0,5

58,8

42,4

18,8

180 00 05,4

ш, = +5,4"

-5,4 00,0

55 19 45,2

55 12 15,1

69 27 52,6

+2.0

+ 1.7

+3,4

47,2

16,8

56,0

179 59 52,9

7,1"

+Л1

00,0

33 44 19,4

103 13 43,4

43 02 01,7

-2,8

-2,1

+0,4

16,6

41.3

02,1

180 00 04,5

«и, =+4,5*

—4,5

00,0

Таблица 120

Номера углов

Значения углов

Уравненные углы

65°53'45,2"

55 12 15,1

103 13 43,4

65°53'42,4"

55 12 16,8

103 13 41,3

Исходный угол

224 19 43,7

224 19 40,5=+3,2"

224 19 40,5

О>4 = 0

= 3,2"

Таблица 121

Номера

углов

Значения

углов

Логарифмы

синусов

Номера

углов

Значения

углов

Ло'гаоифмы

син усов

64°36'00,9"

55 19 45,2

33 44 19,4

9.955 8499

9.915 1012

9.744 6110

3.329 5004

+Ю.0

+14,3

+31,5

49°30'19,3"

69 27 52,6

43 02 01,7

9.881 0802

9.971 4873

9.834 0579

3.258 4263

+18,0

+ 7,9

+22,6

2.945 0625

= 10,8 2.945 0517

264

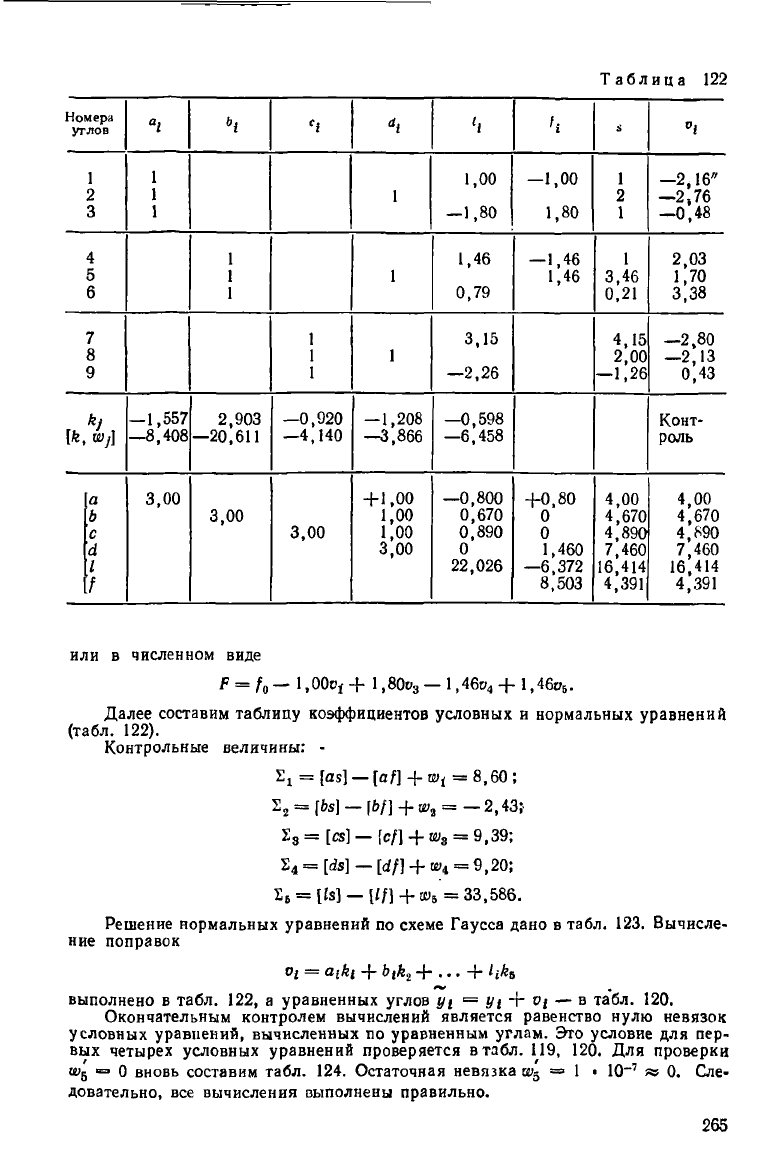
Таблица

118

Номера

углов

1,00

—1,80

—1,00

1,80

—2,16"

—2,76

—0,48

1,46

0,79

— 1,46

1,46

3,46

0,21

2,03

1,70

3,38

3,15

—2,26

4,15

2,00

—1,26

—2,80

—2,13

0,43

—1,557

—8,408

2,903

—20,611

—0,920

—4,140

-1,208

—3,866

—0,598

—6,458

Конт-

роль

д.

3,00

+1,00

1,00

3,00

—0,800

0,670

0,890

22,026

+0,80

1,460

—6,372

8,503

4,00

4,670

4,890

7,460

16,414

4,391

4,00

4,670

4,890

7,460

16,414

4,391

или в численном виде

Р = !

— 1,00Р( + 1,80о

— 1,46Р

+ 1,46о

Далее составим таблицу коэффициентов условных и нормальных уравнений

(табл. 122).

Контрольные величины: -

1 =

[05] — [аЯ+0^ = 8,60;

= [6«]_[&Л+Ш

= -2,43;.

= И-[сЛ +^8 = 9,39;

= № — ЫП + Щ = 9,20;

= — [Щ + = 33,586.

Решение нормальных уравнений по схеме Гаусса дано в табл. 123. Вычисле-

ние поправок

<цк1

+ Ь

{

+ ... +

выполнено в табл. 122, а уравненных углов У1 = У( + — в табл. 120.

Окончательным контролем вычислений является равенство нулю невязок

условных уравнений, вычисленных по уравненным углам. Это условие для пер-

вых четырех условных уравнений проверяется в табл. 119, 120. Для проверки

и>

•= 0 вновь составим табл. 124. Остаточная невязка = 1 • Ю

-7

да 0. Сле-

довательно, все вычисления выполнены правильно.

265

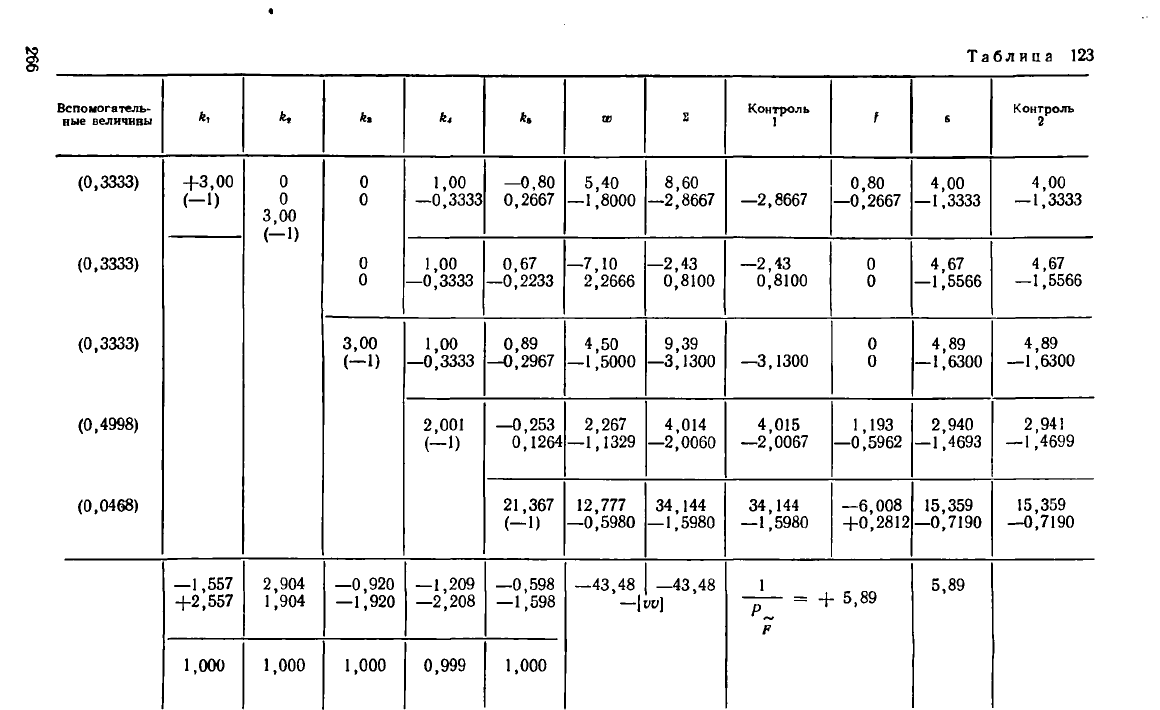
Таблица

143

Вспомогатель-

ные

величины

к,

к.

Контроль

(0,3333)

+3,00

(-1)

3,00

(-1)

1,00

—0,3333

—0,80

0,2667

5,40

—1,8000

8,60

—2,8667

0,80

—0,2667

4,00

—

1,3333

4,00

-1,3333

(0,3333)

3,00

(-1)

1,00

—0,3333

0,67

—0,2233

-7,10

2,2666

—2,43

0,8100

—2,43

0,8100

4,67

—1,5566

4,67

—1,5566

(0,3333)

3,00

(—П

1,00

—0,3333

0,89

—0,2967

4,50

—1,5000

9,39

—3,1300

4,89

—1,6300

4,89

—1,6300

(0,4998)

2,001

(-1)

—0,253

0,1264

2,267

—1,1329

4,014

—2,0060

4,015

—2,0067

1,193

—0,5962

2,940

—

1,4693

2,941

—1,4699

(0,0468)

21,367

(-1)

12,777

—0,5980

34,144

—1,5980

34,144

—1,5980

—6,008

+0,2812

15,359

—0,7190

15,359

—0,7190

-1,557

+2,557

2,904

1,904

—0,920

—1,920

—1,209

—2,208

—0,598

—1,598

—43,48

-1

—43,48

IV]

—= + 5,89

5,89

1,000 1,000 1,000

0,999

1,000

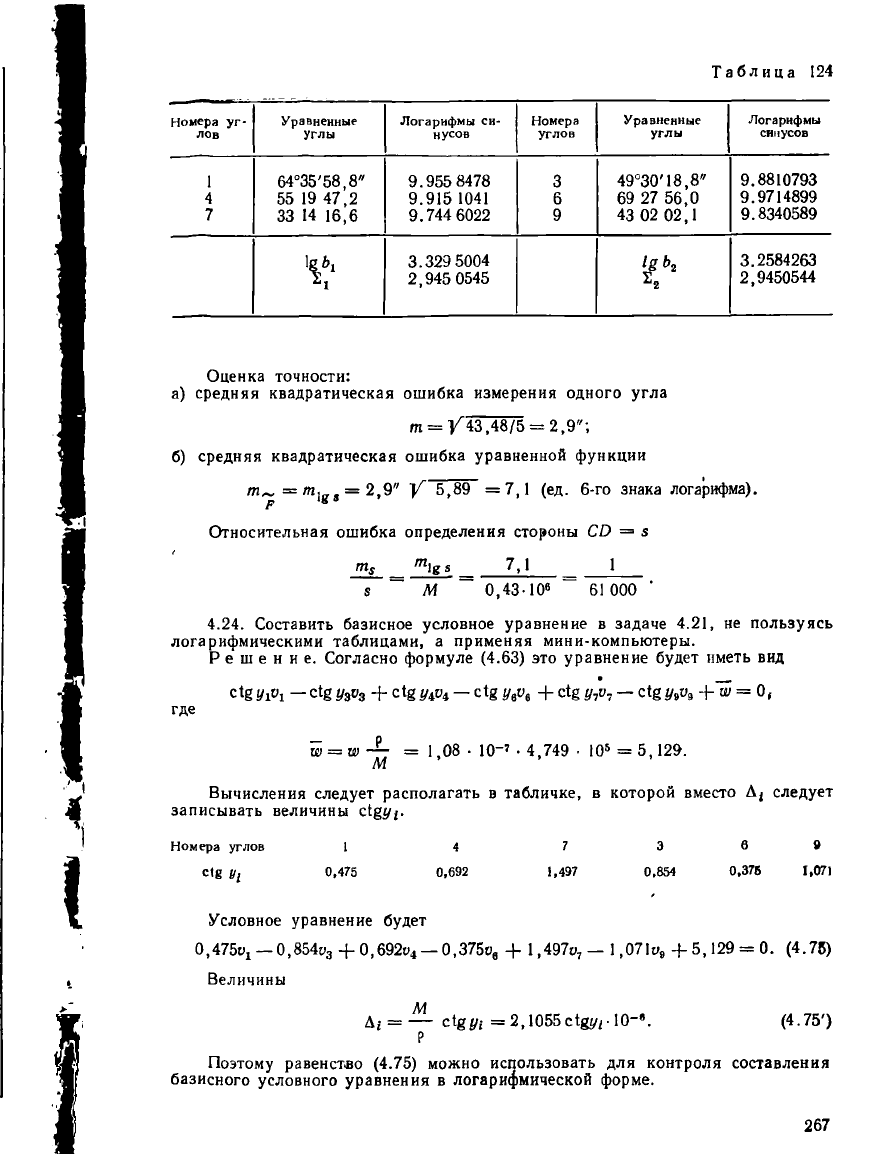
Таблица

118

Номера уг-

лов

Уравненные

углы

Логарифмы си-

нусов

Номера

углов

Уравненные

углы

Логарифмы

синусов

64°35'58,8"

55 19 47,2

33 14 16,6

9.955 8478

9.915 1041

9.744 6022

49°30'18,8"

69 27 56,0

43 02 02,1

9.8810793

9.9714899

9.8340589

3.329 5004

2,945 0545

"г

3.2584263

2,9450544

Оценка точности:

а) средняя квадратическая ошибка измерения одного угла

т =/43,48/5 = 2,9";

б) средняя квадратическая ошибка уравненной функции

= т,

8а

= 2,9" / 5,89 =7,1 (ед. 6-го знака логарифма).

Относительная ошибка определения стороны СО = з

т,е$

'' _

8 М 0,43-10

61000 '

4.24. Составить базисное условное уравнение в задаче 4.21, не пользуясь

логарифмическими таблицами, а применяя мини-компьютеры.

Решение. Согласно формуле (4.63) это уравнение будет иметь вид

• .

с*8 УЛ

—

с!§ (/

с1§

уьщ — с1§ УЛ +

с1§

у^. — с1§ + т = 0,

где

ш = а> — = 1,08 • 10"'• 4,749 • 10

= 5,129.

Вычисления следует располагать в табличке, в которой вместо Д

следует

записывать величины с^ёУг-

Номера углов 1 4 7 3 в в

с!в У

0,475 0,692 1,497 0,854 0,37В 1,071

Условное уравнение будет

0,475о

— 0,854о

+ 0,692о

— 0,375о

+ 1,497о

—

,071у

+ 5,129 = 0. (4.75)

Величины

д, = — сЪп = 2,1055 с1й(//

•

_в

. (4.75')

Поэтому равенство (4.75) можно использовать для контроля составления

базисного условного уравнения в логарифмической форме.

267

Таблица

118

Номера

треугольников

Номера уг-

лов

Измеренные углы

«1

Поправки

Уравненные углы

147°40'06,2"

12 48 113,6

19 31 44,9

—0,3"

—6,4

+1.9

147°40'06,0"

12 48 07,2

19 31 46,8

180 00 04,7

01,=+4,7

73 43 55,2

58 36 48,8

47 39 15,8

-4,7

—0,8"

+0,5

180 00 00,0

73 43 54,4

58 36 49,3

47 39 16,3

III

179 59 59,8

ш,=—0,2

67°23'18,7

67 16 22,0

45 20 20,7

+0,2

—1,5

-0,0

+0,1

180 00 000

67 23 17,2

67 16 22,0

45 20 20,8

180 00 01,4

=+1,4

43 24 13,4

86 26 43,0

50 09 06,5

—1.4

-2,4

—2,2

-0,3

180 00 00 0

43 24 11,0

86 26 42,8

50 09 06,2

18000 02,9

цу

=+ 2,9

-2,9

180 00 00 0

4.25. Выполнить уравнивание углов коррелатны.м способом'по одному из

вариантов задачи 3.29. Исходные данные: Ь

= 2637,070, Ь

= 2273,075, ^А =

^ 192°56'57,5". Оценить точность уравненной стороны СГ>.

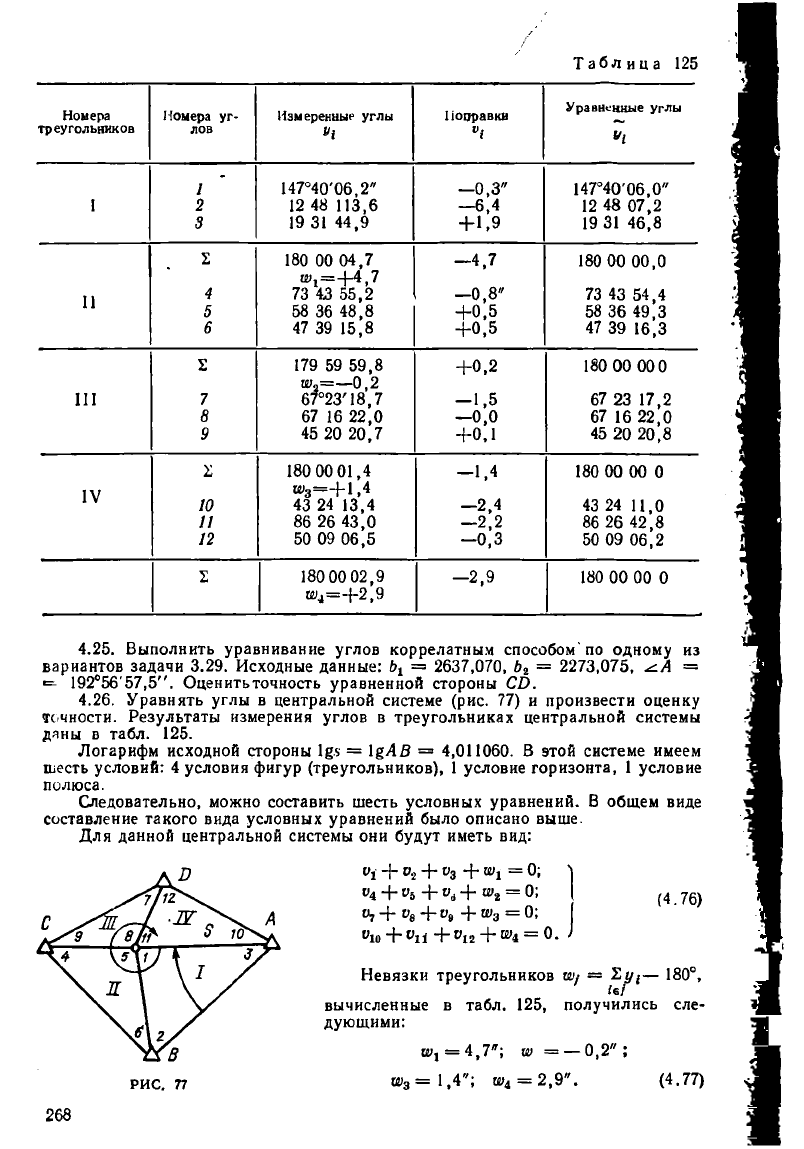
4.26. Уравнять углы в центральной системе (рис. 77) и произвести оценку

точности. Результаты измерения углов в треугольниках центральной системы

дяны в табл. 125.

Логарифм исходной стороны = 16-4В = 4,011060. В этой системе имеем

шесть условий: 4 условия фигур (треугольников), 1 условие горизонта, 1 условие

полюса.

Следовательно, можно составить шесть условных уравнений. В общем виде

составление такого вида условных уравнений было описано выше.

Для данной центральной системы они будут иметь вид:

+ °з + Щ = 0; 1

04 + +

+ Щ = 0; I

0? + 0

+0» + ^з = о; |

010

011

+012 + ^4 = 0- 1

(4.76)

РИС. п

Невязки треугольников ау = — 180°,

вычисленные в табл. 125, получились сле-

дующими:

ш, = 4,7"; т = — 0,2";

и>

= 1,4"; щ = 2,9". (4.77)

268

Таблице 126

Значения

углов

Логарифмы

синусов углов

Номера

углов

Значения

углов

Логарифмы

синусов углав

12°48'13,6"

73 43 55,2

67 23 18,7

43 24 13.4

9.3455948

9.9822540

9.9652644

9.8370419

19°31'44,9"

47 39 15,8

45 20 20,7

50 09 06,5

9.5241185

9.8687003

9.8520401

9.8852169

=Э. 1301551 2„=9.1300758

о), = —Е

= -{- 793 ед. 7-го знака логарифма.

Свободный член условного уравнения горизонта (углы при точке О) вычис-

лен ниже.

Номера углов Измеренные значения углов

1 147°40'06,2*

5 58 36 48,8

8 67 16 22,0

11 86 26 43.0

Е 360 00 00,0, «г,=0,0

Значения свободного члена щ и коэффициентов при поправках получены

в табл. 126 при использовании семизначных таблиц логарифмов.

Коэффициенты и свободный член полюсного уравнения выразим в единицах

пятого знака логарифма. Окончательное полюсное условное уравнение получит

вид

+ 0,926а, — 0,593о

+ 0,061 о

— 0,192о

+ 0,087», — 0,208о

+ О,223о

— 0, 175О

+ 7,93 =0.

Учитывая выражения (4.76) и (4.77), в окончательном виде условные урав-

нения поправок запишутся так:

V1 +р2 + «3+

= 0; »10+

'и + "п +2,9 = 0;

«4+"5 +"в —°.2 = 0; + »в + »в + =0:

+»»++1.

= о;

0,926о

— 0,593о

+ 0,061 о

— 0,192о

+ 0,087о, — 0,208о

+ 0,223о

Х0

—

— 0, 175в

+ 7,93 = 0.

Центральная система, изображенная на рис. 77, опирается на исходную

сторону АВ = 5. После уравнивания углов этой системы можно вычислить дли-

ны всех сторон треугольников. Длины сторон являются функциями уравненных

углов и исходной стороны АВ. Пусть требуется определить относительную ошиб-

ку стороны ОА = 5. Выбрав направление подхода к стороне ОА, показанное на

рис. 77, получим Р = Р

— Д

+ Д

С учетом того, что изменение логарифма синуса первого угла на 1" будет

равно —3,32 ед. 6-го знака логарифма, так как величина угла больше 90

(147°40'06,2"), функция будет иметь вид Р = 3,320, + 9,26У

+ Р

Далее составим табл. 127, 128 коэффициентов условных и нормальных

уравнений.

269

Таблица 118

Номера

углов

г 3

1 1

0,332

2,332

—0,28

2 1

0,926

2,852

—6,40

3 1

—0,593

0,926

0,407

1,94 —0,593

—4,74

+0,061 1,061

—0,85

5 1

+0,061

2,000

0,50

—0,192 0,808

0,55

0,808

0,20

1 +0,087

1,087

1,51

2,000 —0,02

1 —0,208

0,792

+0,13

—1,40

+0,223

1,223

—2,45

2,000

—0,20

1 —0,175

0,825

—0,25

О)

—1,290

4,7

—0,512

-6,2

— 1,026

1,4

—1,215

2,9

1,011

—5,577

7,93

М=54,61

+54,75

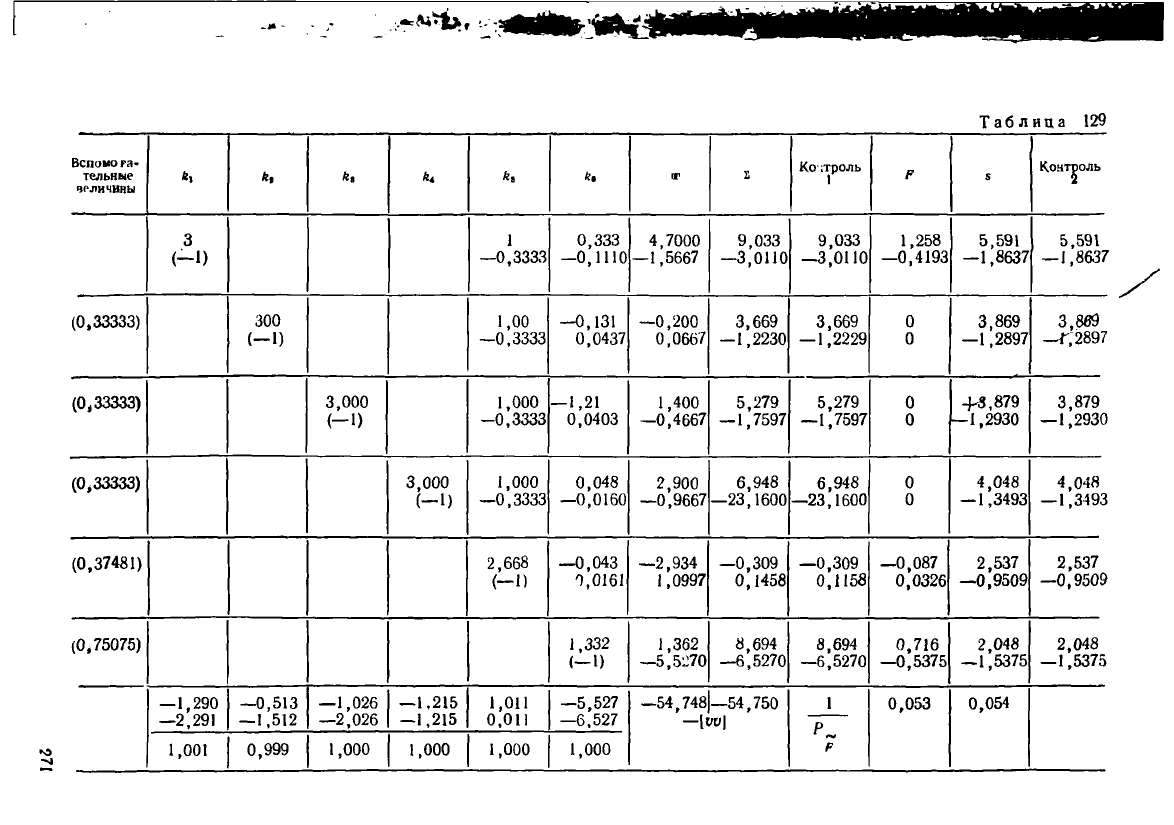
Решение нормальных уравнений коррелат выполнено в табл. 129 по схеме

Гаусса. Поправки приведены в табл. 127. Окончательный контроль вычислений

здесь опущен (остаточную нрвязку полюсного условного уравнения вычислить

самостоятельно).

Таблица 128

я]

Ь] с]

«1

Конт-

роль

(2* л

0,333

—0,131

—0,121

0,048

1,382

1,258

0,332

0,857

5,591

3,869

3,879

4,048

8,332

2,368

5,591

3.86Л

3,879

4,048

8,332

2,368

4 7

-0,2

1,4

2,9

7,93

9,033

3,669

5,279

6,949

8,000

9,441

0,967

3,414

Нормальные уравнения коррелат

I- 3*, +А

+0,333 А,+ 4,70=0,

2. 3*

_ о, 131 А, -0,20=0,

3- З*

0,121 6,+1,40=0,

+ 0,048 *

+ 2.90=0,

5. А, + й

+ /г

+ + 0 6„ + 0,00=0,

6. +0,333^—0.131А,—0,121Аз + 0,048Й

+ 0Й

+ 1,382 *„+7.93=0.

270

Таблица

129

Вспомога-

тельные

величины

к,

к, к.

к.

(Г

Ко- ;троль

Контроль

(-1)

—0,3333

0,333

—0,1110

4,7000

—

1,5667

9,033

—3,0110

9,033

—3,0110

1,258

—0,4193

5,591

—1,8637

5,591

—

1,8637

(0,33333)

300

(-1)

1,00

—0,3333

—0,131

0,0437

-0,200

0,0667

3,669

—1,2230

3,669

—

1,2229

3,869

—1,2897

3,8в9

—Г,2897

(0,33333)

3,000

(-1)

1,000

-0,3333

— 1,21

0,0403

1,400

—0,4667

5,279

—

1,7597

5,279

—1,7597

4-3,879

—1,2930

3,879

—1,2930

(0,33333)

3,000

(-1)

1,000

—0,3333

0,048

—0,0160

2,900

—0,9667

6,948

—23,1600

6,948

—23,1600

4,048

—

1,3493

4,048

—1,3493

(0,37481)

2,668

(-1)

—0,043

0,0161

—2,934

1,0997

—0,309

0,1458

—0,309

0,1158

—0,087

0,0326

2,537

—0,9509

2,537

—0,9509

(0,75075)

1,332

(-1)

1,362

—5,51:70

8,694

—6,5270

8,694

—6,5270

0,716

—0,5375

2,048

—1,5375

2,048

—1,5375

—1,290

—2,291

—0,513

— 1,512

—1,026

—2,026

— 1,215

—1,215

1,011

0,011

—5,527

—6,527

—54,748|—54,750

-М

0,053

0,054

1,001

0,999

1,000

1,000 1,000

1,000

Оценка/точности:

Средняя квадратическая ошибка резуль- .

тата непосредственного измерения (одного

угла) 7

т = = У 54,56/6 = 3,0".

ТочносН. определения средней квадрати-

ческой ошибки

^ М _

. т

= 0,Ь/ .

У 2 г У12

Средняя квадратическая ошибка лога-

рифма стороны 5 •= ОА

1ев

= т

>° КМ53 = 0,69;

=т

= 0,87 х /0,053 = 0,20.

Относительная ошибка определения стороны 5 = О А

т,

10"

0,69

0,434

10"

63 000

т„

"18 8

217 000

4.27. Уравнять коррелатным способом углы в геодезическом четырехуголь-

нике (рис. 78) и оценить точность определения диагонали ВО, принимая вторую

диагональ АС за безошибочную.

В этом построении возникает четыре условных уравнения:

фигур

+ + «з +

+ = 0;

о»

1>„

+ ш

= 0;

+ Ч + щ + ^ + щ = 0:

полюсное, составленное в виде (4.63),

2 2 с1ёу

+ щ = 0.

I" 1,3,5,7 1—2, 4, 6,8

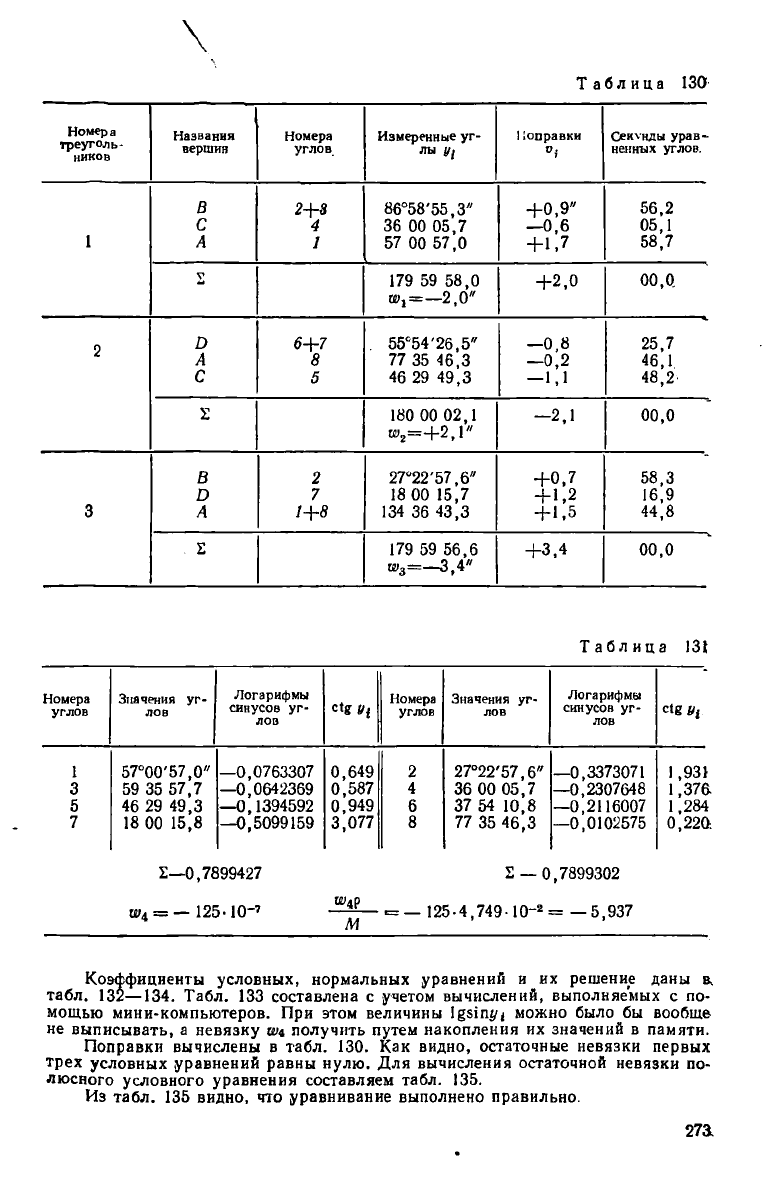
Вычисление невязок и величин выполнено в табл. 130 и 131.

Полюснор условное уравнение имеет вид:

0.649&, — 1,931о

+ 0,587о

—

,376У

+ 0,949О

— 1,284ц, +

+ 3,077к, — 0,22(Ь

— 5,937 = 0.

Оцениваемая функция имеет вид

Р = Р

+ УЛ ~

с1

(Уг

Уз)

(«2 + °з) + (у

Уъ)

(»4 + «в) — у

если диагональ вычислять по треугольникам А ВС и ВСО, или

Р = Р

+ 0,649»! — 0,053а, — 0,053о

+ 0,132о

— 1,284о„.

272.

Таблица

118

Номера

треуголь-

ников

Названия

вершин

Номера

углов

Измеренные уг-

лы у

{

] [оправки Сек\'нды урав-

ненных углов.

2+8

86°58'55,3"

36 00 05,7

57 00 57,0

+0,9"

-0.6

+1,7

56,2

05,1

58,7

179 59 58,0

щ=—2,0"

+2,0

00,0.

6+7

. 55°54'26,5"

77 35 46,3

46 29 49,3

—0,8

—0,2

— 1,1

25,7

46.1

48.2

180 00 02,1

=+2,1"

—2,1

00,0

1+8

27°22'57,6"

18 00 15,7

134 36 43,3

+0,7

+1.2

+1.5

58,3

16,9

44,8

179 59 56,6

в,=-3,4"

+3,4 00,0

Таблица 131

Номера

углов

Значения

лов

уг-

Логарифмы

синусов уг-

лов

с<8

Номера

углов

Значения уг-

лов

Логарифмы

синусов уг-

лов

57°00'57,0"

59 35 57,7

46 29 49,3

18 00 15,8

—0,0763307

—0,0642369

—0,1394592

—0,5099159

1—0,7899427

щ = — 125-10"'

0,649

0,587

0,949

3,077

Щ?

27°22'57,6"

36 00 05,7

37 54 10,8

77 35 46,3

—0,3373071

—0,2307648

—0,2116007

—0,0102575

1 — 0,7899302

: — 125-4,749-Ю-

= —5,937

1,931

1,376

1,284

0,220.

Коэффициенты условных, нормальных уравнений и их решение даны в.

табл. 132—134. Табл. 133 составлена с учетом вычислений, выполняемых с по-

мощью мини-компьютеров. При этом величины 1§51Ш/| можно было бы вообще

не выписывать, а невязку ш получить путем накопления их значений в памяти.

Поправки вычислены в табл. 130. Как видно, остаточные невязки первых

трех условных уравнений равны нулю. Для вычисления остаточной невязки по-

люсного условного уравнения составляем табл. 135.

Из табл. 135 видно, что уравнивание выполнено правильно.

270