Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

Контроль вычислений:

[аЛ] = [ч] = 0; [ай] = [й = 0.

Примечание. Центральные координаты достаточно вычислять с точ-

ностью до 1 м. Поэтому а

(

и 5; в таблице приведены с точностью до 0,1 и 1 м.

5.6. Доказать справедливость формул

Р1

(*, _

у = \рх*]-х[рхг] = А,

1=1

2] Р1 (У1 — у)

= [РУ

]—УШ = В,

(5 25>

Р1

(*» —

)(У1 — у) = [рху] — X [ру] = [рху] — у[рх] = С.

1=1

Формулы (5.25) запрограммированы для калькулятора «Электроника БЗ-21»

(см. прил. XIII.15). По этой программе можно выполнить обработку равноточ-

ных и неравноточных измерений, вычислить коэффициент корреляции г

ху

и вто-

рые слагаемые в формуле (4.70).

5.7. Доказать, что при Р( = 1 справедлива формула (см. задачу 5.6)

__С

АВ ~

Гху

где г,у — коэффициент корреляции между случайными величинами X и К.

5.8. Доказать, что -цхг = [Н.г-Л, т.е. что обратный вес предварительно

уравненных измерений является весом до уравнивания в группе 2. Убедиться

в этом для функции 1§« (в = СО) в задаче 5.2.

§ 45. СПОСОБ КРЮГЕРА — УРМАЕВА

Как мы уже отмечали, цель применения двухгруппового способа

уравнивания заключается в уменьшении числа совместно решаемых

уравнений. При этом общая система уравнений распадается на две

не связанные между собой системы. Это дает возможность распреде-

лить вычисления на нескольких исполнителей или сэкономить память

ЭВМ. Вместе с тем, двухгрупповое уравнивание требует преобразо-

вания коэффициентов условных уравнений второй группы. Поэтому

его применение будет эффективным, если этот процесс не требует трудо-

емких вычислений. Учитывая это, в первую группу относят те услов-

ные уравнения, которые не содержат общих поправок. Тогда уравни-

вание в первой группе сводится к независимому решению каждого

условного уравнения и применению простых формул для вычисления

преобразованных коэффициентов условных уравнений второй группы.

Наиболее прост двухгрупповой способ применительно к уравни-

ванию сетей триангуляции, в которых измерены отдельные углы (его

называют способом Крюгера — Урмаева). В самом деле, если в пер-

вую группу отнести условные уравнения фигур треугольников, не со-

держащих общих углов, то для каждого /-го треугольника будем иметь

условное

284.

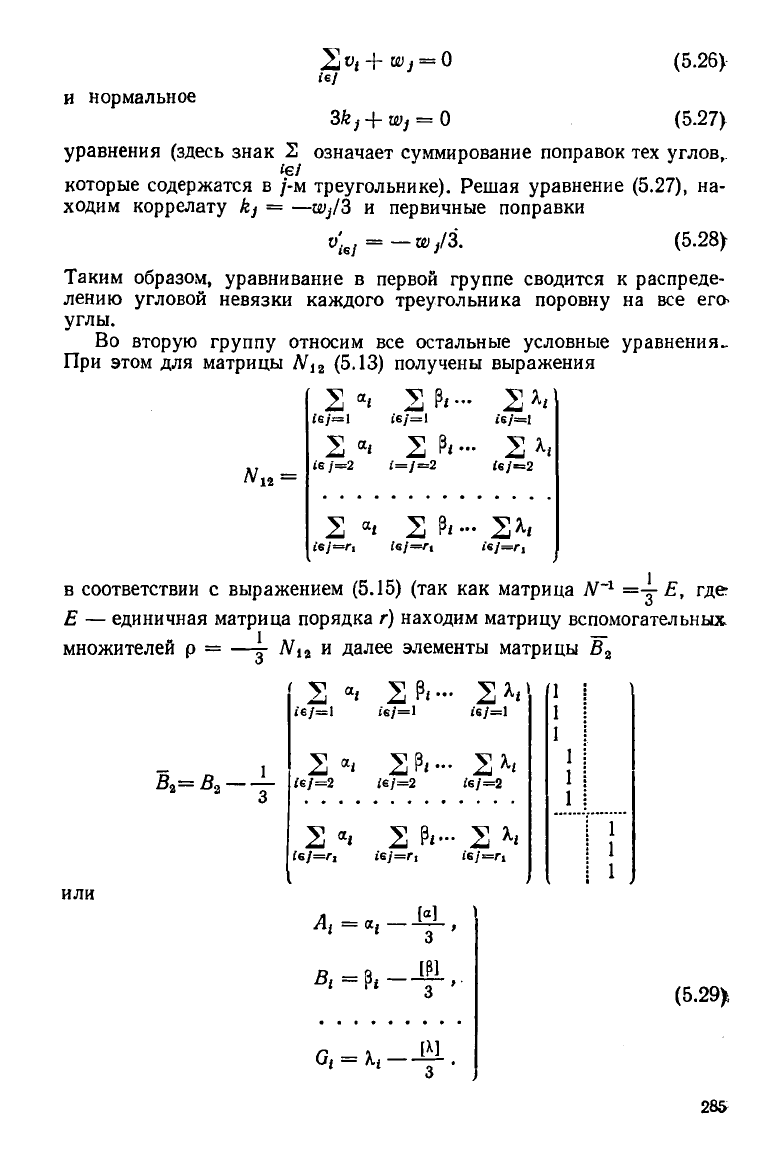
и нормальное

ы>,

— О

+ Ш) = О

(5.26)

(5-27)

уравнения (здесь знак 2 означает суммирование поправок тех углов,

(е/

которые содержатся в /-м треугольнике). Решая уравнение (5.27), на-

ходим коррелату к

}

= —щ/3 и первичные поправки

= — до уз.

(5.28)

Таким образом, уравнивание в первой группе сводится к распреде-

лению угловой невязки каждого треугольника поровну на все его-

углы.

Во вторую группу относим все остальные условные уравнения-

При этом для матрицы УУ

(5.13) получены выражения

2 »1

2 Р« -

2М

ге/=1

('е/=|

("б/=1

2 Р|...

2 я,

»е /=2 1=1=2

1е)=2

2 <ч

2 ?! ...

2 л,

<б/=Г,

1е!=Г1

'«/=/• 1

в соответствии с выражением (5.15) (так как матрица /V"

=у Е, где

Е — единичная матрица порядка г) находим матрицу вспомогательных

множителей р = —^ Ы

хг

и далее элементы матрицы В

Д>= 5, —

2 Р«-

2 V

<"е/=1

Ы]'=\

1б/=1

< 2Р< -

1е}=2 1*1=2 1ч 1=2

2 «1 2 й-

1е/=г,

16 /=Г,

или

А -а -М.

(5.29>

285.

Опустив здесь индексы у сумм, мы предполагаем, что они вычис-

ляются отдельно в каждом треугольнике, а [а], [Р], ..., [Я] означают

сумму коэффициентов а

, р

, ..., при поправках углов, которые

входят в этот треугольник. Аналогично для оцениваемой функции

получены преобразованные коэффициенты р

= — Контролем

вычислений служат равенства [А] = [В] = ... = [О] == [/"Ч = 0, вы-

текающие из условия (5.6). Выполнение этих равенств сразу следует

из (5.29), так как коэффициенты А

{

, ..., суть уклонения от

простой арифметической средины (см. § 20).

При уравнивании геодезического четырехугольника условные

уравнения фигур, которые относят в первую группу, имеют вид (см.

рис. 72).

+ V

-\-V•

+ Ы)

= 0,

в + Щ + 1>

+ Щ — 0.

В этом случае первичная поправка будет равна

°(Ч

~ "Т"' <

°)

а коэффициенты условных уравнений второй группы (фигуры и по-

люсного) в отличие от (5.29) необходимо вычислять по формулам

4 = 5, = ?,--Ш-. (5.31)

Двухгрупповой коррелатный способ уравнивания применяют при

уравнивании одиночных полигонометрических ходов и сетей с исход-

ными дирекционными углами на узлах. В этом случае первичная по-

правка в каждый угол хода равна у/ = /(/1+1), а преобразование

условных уравнений второй группы сводится к вычислению централь-

ных координат отдельно в каждом ходе (см. § 44).

5.9. Выполнить двухгрупповое уравнивание углов, измеренных в централь-

ной системе, по условиям задачи 4.26.

Решение. Воспользуемся результатами вычислений, выполненных в за-

даче 4.26. Отнеся в первую группу четыре условных уравнения фигур, согласно

(5.28) получаем первичные поправки:

»1 = = »'з= —

"' °7 = »в = "9 = — -^— = —0,47",

^ = Ч = V, = = 0,07",

[

= с-п = 4 = - = - 0,97'.

Предварительно уравненные углы приведены в табл. 140.

Коэффициенты условных уравнений второй группы (горизонта и полюсно-

го), очевидно, будут теми же, что и в задаче 4.26. Для вычисления преобразован-

ных невязок этих условных уравнений воспользуемся предварительно уравнен-

ными углами (см. табл. 140 и 141)

286.

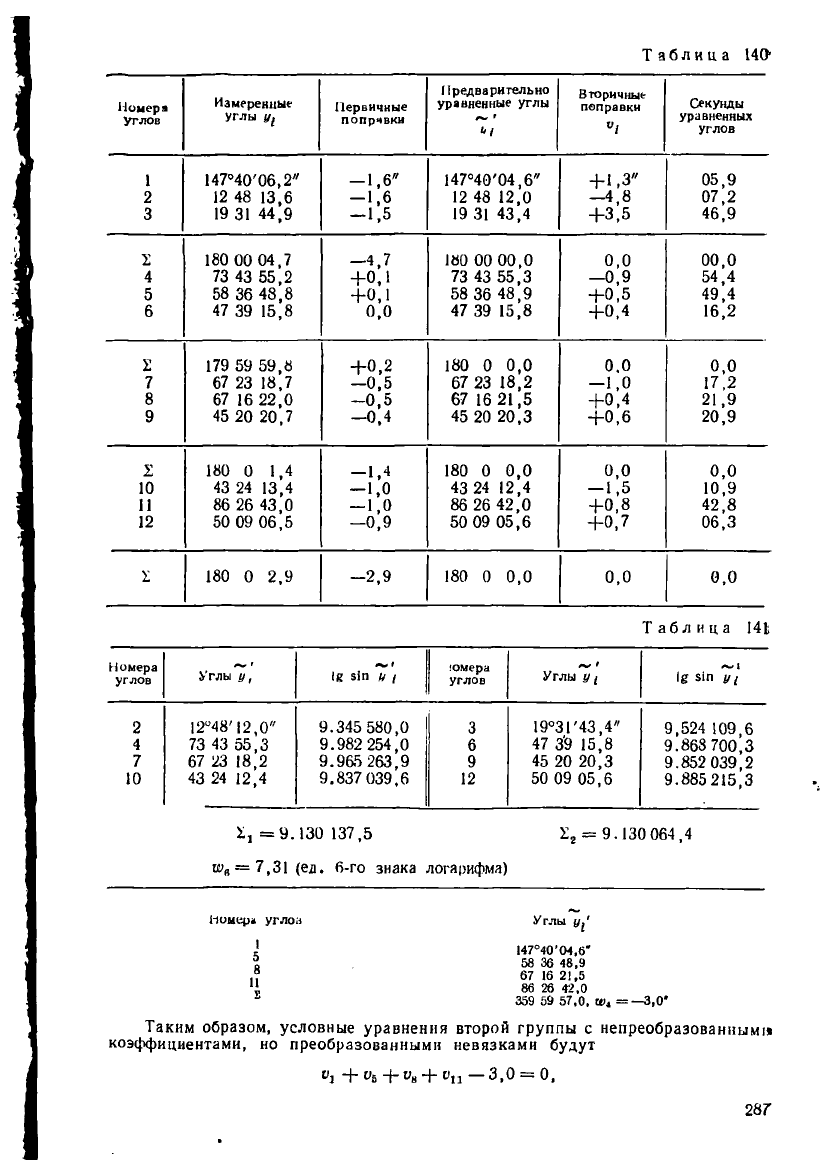
Таблица 143

Номера

Углов

Измеренные

Углы у

Первичные

попрчвки

Предварительно

уравненные углы

•<1

Вторичные

поправки

Секунды

уравненных

углов

147°40'06,2"

12 48 13,6

19 31 44,9

— 1,6"

-1,6

-1,5

147°40'04,6"

12 48 12,0

19 31 43,4

+ 1,3"

—4,8

+3,5

05,9

07,2

46,9

180 00 04,7

73 43 55,2

58 36 48,8

47 39 15,8

-4,7

+0,1

0,0

180 00 00,0

73 43 55,3

58 36 48,9

47 39 15,8

0,0

—0,9

+0,5

+0,4

00,0

54,4

49,4

16,2

179 59 59,8

67 23 18,7

67 16 22,0

45 20 20,7

+0,2

—0,5

-0,5

-0.4

180 0 0,0

67 23 18,2

67 16 21,5

45 20 20,3

0.0

-1,0

+0,4

+0,6

0,0

17,2

21,9

20,9

180 0 1,4

43 24 13,4

86 26 43,0

50 09 06,5

-1.4

—1,0

— 1,0

—0,9

180 0 0,0

43 24 12,4

86 26 42,0

50 09 05,6

0,0

-1,5

+0,8

+0,7

0,0

10,9

42,8

06,3

X 180 0 2,9 —2,9 180 0 0,0

0,0

Таблица 141

Номера

углов

Углы у,

18 з'ч и

юмера

углов

Углы у 1

л- 1

1е 5'

12"48' 12,0"

73 43 55,3

67 23 18,2

43 24 12,4

9.345 580,0

9.982 254,0

9.965 263,9

9.837 039,6

19°31'43,4"

47 3'9 15,8

45 20 20,3

50 09 05,6

9,524 109,6

9.868 700,3

9.852 039,2

9.885215,3

=9.130 137,5 Г„ = 9.130 064,4

= 7,31 (ед. 6-го знака логарифма)

Номер» углоа Углы

} 147°40'(М,6"

о 58 36 48,9

° 67 16 2!,5

'' 86 26 42,0

359 59 57,0, о>

= —3,0*

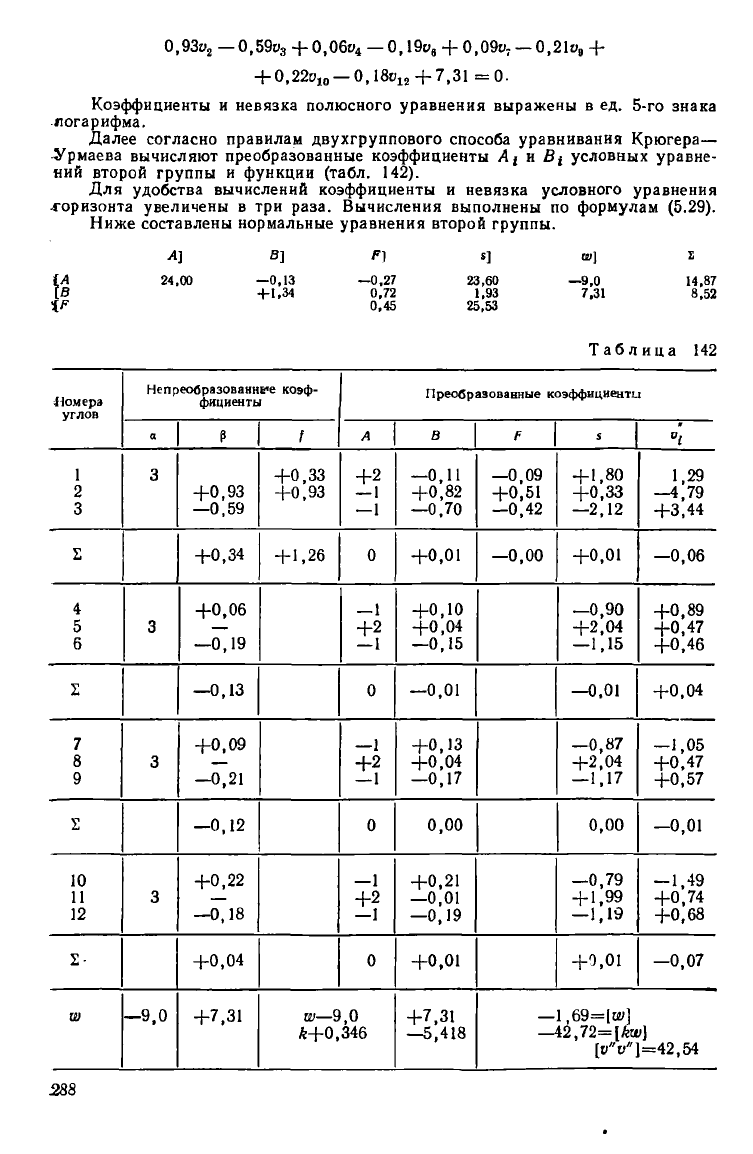
Таким образом, условные уравнения второй группы с непреобразованным!»

коэффициентами, но преобразованными невязками будут

+Св+«8 + Оц—3.0 = 0,

0,93о

— 0,59о

+ о, 06о

— 0,19к

+ 0,09о

— 0,21 о

+ 0,22о

1о

— 0,18о

+ 7,31 =0.

Коэффициенты и невязка полюсного уравнения выражены в ед. 5-го знака

логарифма.

Далее согласно правилам двухгруппового способа уравнивания Крюгера—

Урмаева вычисляют преобразованные коэффициенты и условных уравне-

ний второй группы и функции (табл. 142).

Для удобства вычислений коэффициенты и невязка условного уравнения

•горизонта увеличены в три раза. Вычисления выполнены по формулам (5.29).

Ниже составлены нормальные уравнения второй группы.

А] В] Щ 5] со] Е

(Л 24,00 —0,13 —0,27 23,60 —9,0 14,87

[В +1,34 0,72 1,93 7,31 8,52

0,45 25,53

Таблица 142

Ломера

углов

Не преобразованное коэф-

фициенты

Преобразованные коэффициента

Ломера

углов

°1

+0,93

—0,59

+0,33

+0,93

— 1

-0,11

+0,82

—0,70

—0,09

+0,51

—0,42

+1,80

+0,33

—2,12

1,29

—4,79

+3,44

I +0,34

+ 1,26

0 +0,01

—0,00

+0,01

—0,06

+0,06

—0,19

— 1

+0,10

+0,04

—0,15

—0,90

+2,04

-1,15

+0,89

+0,47

+0,46

—0,13

—0,01 —0,01 +0.04

+0,09

—0,21

—1

+0,13

+0,04

—0,17

—0,87

+2,04

— 1,17

—1,05

+0,47

+0,57

—0,12

0,00 0,00

—0,01

+0,22

—0,18

—1

+0,21

—0,01

—0,19

—0,79

+ 1,99

-1,19

—1,49

+0,74

+0,68

+0,04

0 +0,01

+0,01

—0,07

-9,0

+7,31

он—9,0

й+0,346

+7,31

—5,418

—1,69=[ш]

—42,72=[йш]

[и"1>"]=42,54

288.

Таблица 143

Е Р г

Контроль

24,00

— 1

(0,41(67)

—0,13

+0,0054

1,34

—1

—9,00

+0,375

+7,26

—5,418

14,87

—0,620

8,60

—6,418

—0,27

+0,0112

+0,72

—0,537

23,60

—0,9833

+2,06

—1,537

23,60

—0,9833

2,06

—1,537

к 0,346

к—0,654

—5,418

—6,418

—42,71

[V"

—42,70

+0,050

РР

Нормальные уравнения второй группы будут:

24,00^—0,13^—9,0 = 0,

— 0,136,, + 1,34й

+7,31 =0.

Их решение представлено в табл. 143.

Вторичные поправки вычислены по формуле = А + В

(

в табл.

142 и с округлением перенесены в табл. 140. Контролем их вычисления является

выполнение в пределах точности вычислений для каждого треугольника равенств

[[>"] = 0. В ней же вычислены окончательно уравненные углы.

Окончательный контроль вычислений здесь опущен, так как он выполнен

в задаче 4.26. Это же относится и к оценке точности измерений и их функций

Здесь вычислим лишь величину

[и>] = [о'р'] + [1>"0"] = 10,80 + 42,54 = 53,34.

5.10. В задаче 5.9 убедиться в справедливости равенства (5.23), вычислив

[от] непосредственно.

5.11. Решить двухгрупповым способом задачу 4.27.

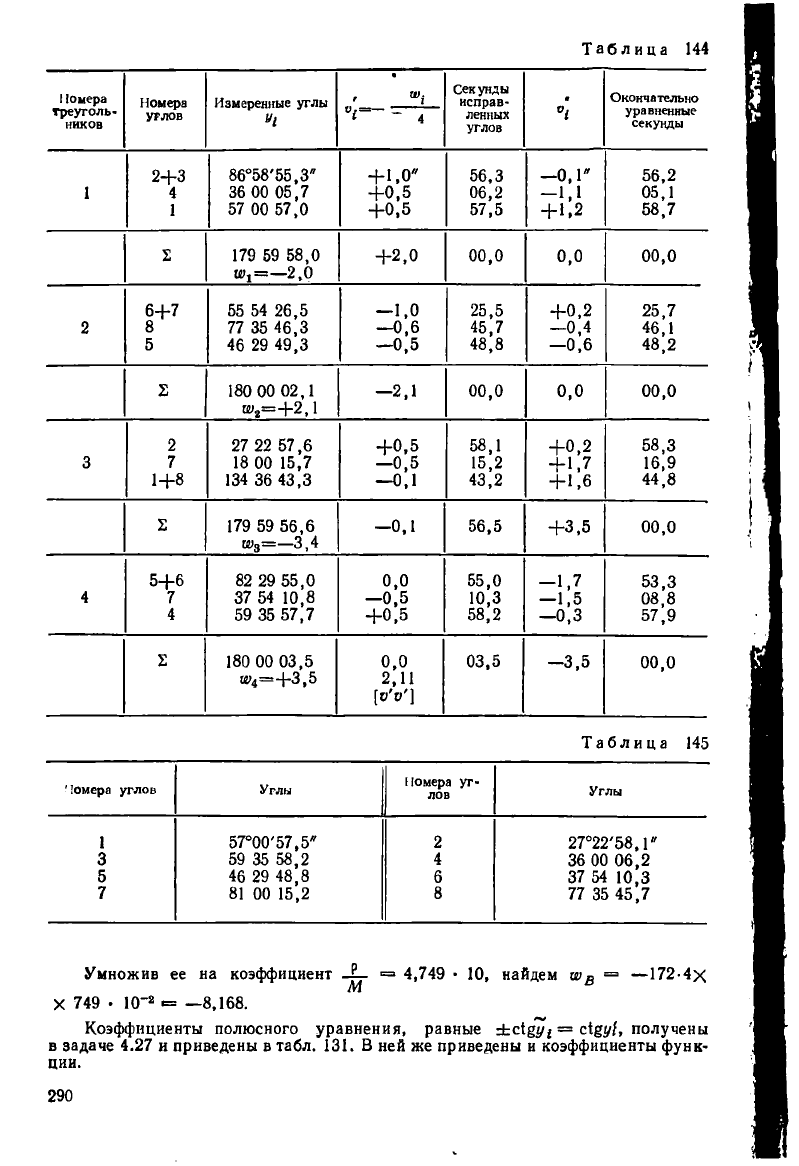
Решение. Вычисления начинаем с составления табл. 144, в которой

вычисляем первичные поправки углов по формуле (5.30), относя в первую груп-

пу условные уравнения фигур треугольников 1 и 2, не содержащих общих углов

Эти поправки находят из любых двух неперекрывающихся треугольников,

например из первого и второго. Для одиночных углов этих треугольников пер-

вичная поправка равна одной четверти невязки треугольника, взятой с обратным

знаком. На двойные углы берется сумма поправок углов, входящих в двойной

угол. Поправка, не равная точно одной четверти невязки, вносится в наиболь-

ший угол. Например, во втором треугольнике, невязка которого оказалась

+2,1", поправка в первый (наибольший) угол равна —0,6", во второй —0,5"

и для суммы углов 7+8 взята —1,0".

В третьем и четвертом треугольниках для углов уже найдены первичные по-

правки при распределении невязок первого и второго треугольников, остается

их только ввести. После этого невязки второй пары смежных треугольников не

устранятся, а лишь изменятся.

Условие фигуры для одного из этих треугольников, например 3, относят

во вторую группу условных уравнений.

Свободный член полюсного уравнения вычислим с помощью вспомогатель-

ной табл. 145 на калькуляторе, применяя метод накопления, или по программе,

приведенной в прил. XIII.7. Она получена равной ш

= —172 • 10~

10-

258

289

Таблица

118

]Омера

треуголь-

ников

Номера

углов

Измеренные углы

«1

'Л- -

Секунды

исправ-

ленных

углов

Окончательно

уравненные

секунды

2+3

86°58'55,3"

36 00 05,7

57 00 57,0

+ 1,0"

+0,5

56,3

06,2

57,5

—0,1"

-1,1

+1.2

56,2

05,1

58,7

179 59 58,0

ш,=—2,0

+2,0 00,0

0,0 00,0

6+7

55 54 26,5

77 35 46,3

46 29 49,3

—1,0

—0,6

-0,5

25,5

45.7

48.8

+0,2

—0,4

-0,6

25,7

46.1

48.2

180 00 02,1

оу=+2,1

—2,1

00,0 0,0 00,0

1+8

27 22 57,6

18 00 15,7

134 36 43,3

+0,5

-0,5

-0,1

58.1

15.2

43,2

+0,2

+1,7

+1,6

58,3

16,9

44,8

179 59 56,6

о>з=—3,4

—0,1 56,5

+3,5 00,0

5+6

82 29 55,0

37 54 10,8

59 35 57,7

0,0

-0,5

+0,5

55,0

10,3

58,2

-1,7

-1,5

—0,3

53,3

08,8

57,9

180 00 03,5

«>4=+3,5

0,0

2,11

[о'о']

03,5

-3,5

00,0

Таблица 145

'Юмера углов

Углы

Номера уг-

лов

Углы

57°00'57,5"

59 35 58,2

46 29 48,8

81 00 15,2

27°22'58,1"

36 00 06,2

37 54 10,3

77 35 45,7

Уииожив ее на коэффициент Л- = 4,749 • 10, найдем о»

= —172-4Х

X 749 • 10

-г

•= —8,168.

Коэффициенты полюсного уравнения, равные ±с1ду

= с получены

в задаче 4.27 и приведены в табл. 131. В ней же приведены и коэффициенты функ-

ции.

290

Таблица 146

Номера

• углов

В р §

0,649

—1,931

0,587

—1.376

+0,649

—0,053

0,132

—1

1,167

—1,413

1,105

—0,858

0,480

—0,221

—0,037

2,647

—0,634

—0,116

—1,895

1,20

0,19

—0,31

—1,08

+0,001 0,001

0,949 1

0,318

0,420

—0,262

—0,65

Далее составляем табл. 146 преобразования коэффициентов условных урав-

нений второй группы и под ней — таблицу коэффициентов нормальных уравне-

ний. Левая и правая части первого условного уравнения увеличены в 2 раза с

целью избежать дробных чисел. Невязка а>

вычислена в табл. 130.

5.12. Сделать то же самое в условиях задачи 4.28.

§46. ПАРАМЕТРИЧЕСКИЙ СПОСОБ С ЗАВИСИМЫМИ ПАРАМЕТРАМИ

В главах 3 и 4 мы рассмотрели два основных способа уравнивания —

параметрический и коррелатный. В практике уравнительных вычисле-

ний встречаются случаи, когда с целью упрощения вычислений применя-

ют комбинации этих способов. Одним из них является параметрический

способ с зависимыми параметрами (условиями). В отличие от мате-

матической постановки задачи уравнивания параметрическим спосо-

бом пусть теперь в качестве параметров выбраны не к необходимых

неизвестных, не связанных никакими точными математическими за-

висимостями, а т~> к неизвестных блг

Ьх

&х

, образующих век-

тор А*, который должен удовлетворять матричному условию В Ах +

+ 1Р = 0.

Таким образом, теперь мы имеем приведенную к линейному виду

систему уравнений поправок и условных уравнений

V = ААх+ Ц (5.32)

ВАх + ха = 0. (5.33)

_ Ясно, что число г условных уравнений должно быть равно разности

г = т — к (оно, конечно, не равно числу избыточных измерений).

Например, если в полигонометрическом ходе в качестве параметров

выбрать не поправки координат определенных пунктов, а поправки

приращений координат, то последние будут связаны двумя простыми

условными уравнениями

10*

291

здесь 7=2 (5 + 1) — 25 = 2.

Уравнения поправок для результатов измерений проще составить

относительно поправок приращений координат, чем координат, хотя

в этом случае и добавляются уравнения (5.34).

Решая уравнения (5.32) и (5.33) под условием Ф = V

РУ = ппп,

составляем функцию

ф = у

РУ — 2 К

{В Ах + Г),

где К — вектор коррелат, а после дифференцирования ее по Ах для

определения минимума приходим к уравнению 2УРА — 2К*В = О,

откуда находим*

РУ + В

К = 0 (5.35)

или с учетом (5.32)

ЯАх + В?К + А

РЬ = 0, (5.36)

где, как и ранее, матрица Я = А

РА.

Объединяя (5.36) и (5.33), получаем систему уравнений

ЯАх + В

К + А'РЬ = 0, |

ВАх + № = 0. |

В подробной записи, обозначив коэффициенты и свободные члены

уравнений поправок (5.32) через а

, Ъ

1г

..., а коэффициенты ус-

ловных уравнений — через Л

, ..., О

будем иметь систему урав-

нений (приняв для простоты р1 = 1):

[аа] Ьх

+ [аЬ] Ьх

+ •.. + [а*] Ьх

+ А& +

+ Я,/г

+ • • • + О

+ [а/] = 0;

[аЬ] Ьх

+ [ЬЬ] 8л:

+ |- Ш Ьх

+ А

+ В

+ • • • +

+ 0

+ [Ы] = 0;

[а*] Ьх

+ [Ь

] Ьх,+ --- + Ш Ьх

+ А

+ В

+ • • • +

+ о

К + Ш = о;

+ А

Ьх

+ (- А

Ьх

+ щ = 0;

В^х, + В

Ьх

+ Ь В

Ьх

+ ш

= 0;

Ъх

+ 0

Ьх

Н + О

Ьх

+ т = 0.

Обобщение леммы Гаусса А

РУ = 0.

292.

Как видно, эта система из-за наличия нулевого блока перед корре-

лятами в г последних уравнениях не является нормальной гауссовой

системой, но обладает свойством симметричности коэффициентов и

может быть решена в схеме Гаусса или метода квадратных корней

(в последнем случае придется иметь дело с мнимыми числами). С при-

менением ЭВМ систему (5.37) целесообразно решать следующим об-

разом. Из первого уравнения находим вектор

Ах = — СГ^К — ОА^РЬ = — О (В

К + А

РЦ, (5.38)

где О = Я"

Подставив выражение (5.38) во второе уравнение (5.37), найдем

— ВОВ

К + № — ВОА'РЬ = О

или ЫК + V? = О, (5.39)

где матрица N = В<2В

, а вектор № = — № +

Заметим, что такая форма уравнивания известна как двухгруппо-

вой способ Бесселя. При этом сначала решают нормальное уравнение

КАх + А

РЬ — 0, не обращая внимания на коррелаты в (5.37), на-

ходят вектор Дл: и матрицу ф, как рассмотрено в § 28, затем^по исправ-

лении измерения вычисляют вектор невязок, совпадающий с вектором

и матрицу N (см. также § 47).

Оценка точности. Необходимая для вычисления средней

квадратической ошибки единицы веса квадратическая форма Ф =

= ]/

РУ = [риь] вычисляется по формуле [рхю\ = [рИ- т\ +

Оценка точности приведенной к линейному виду функции урав-

ненных неизвестных Р — [Ах 4- /

, как и в параметрическом способе,

выполняется по формуле

причем все коэффициенты /

т+1

= /

т+2

= ... = }

+?+1 = 0.

При решении задачи на ЭВМ для оценки ТОЧНОСТИ всех уравненных

неизвестных х

}

(/ = 1, 2, ..., т) находят матрицу весовых коэффици-

ентов

= 0-0ЕГЫ-

В0, (5.40)

которая является также верхним левым блоком обратной матрицы

** ~ [В

0 ) '

Тогда обратный вес любой функции можно найти по формулам

или

= (

)

I р р

для совокупности нескольких функций, аналогичных (3.49). Для ил-

люстрации теории способа решим следующую задачу.

293.