Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

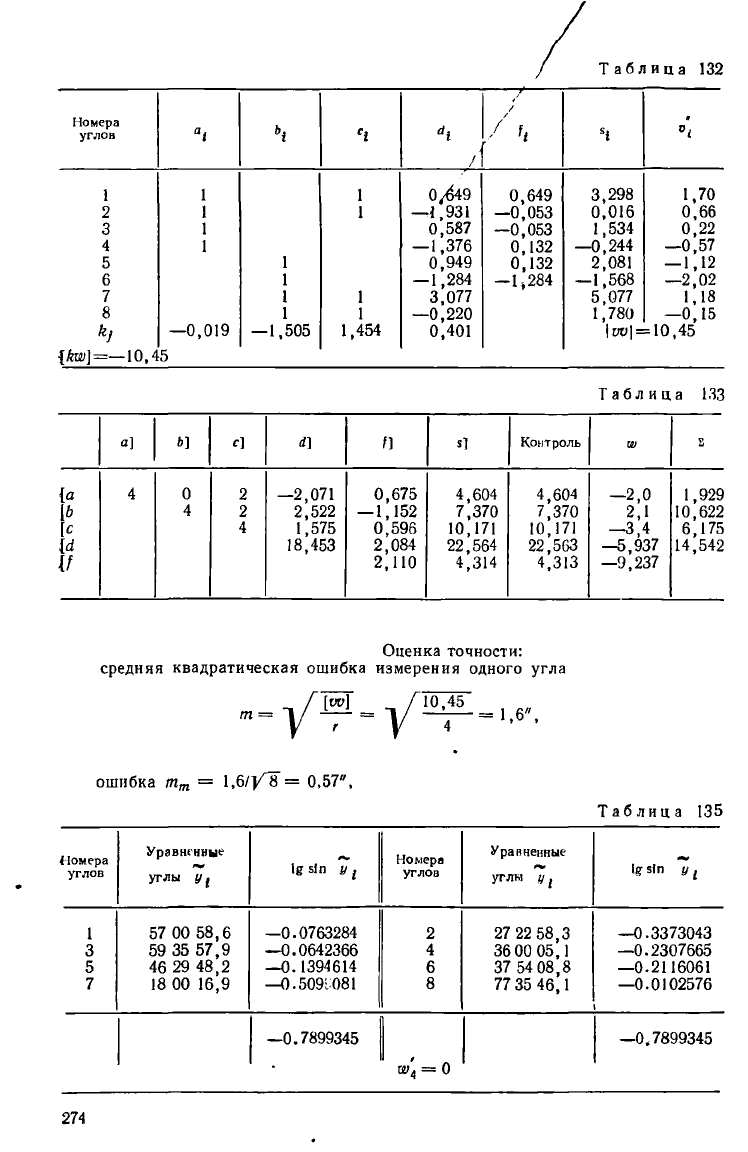
Таблица 118

Номера

углов

к,

—0,019

-1.505

{кш]=—10,45

1,454

0^49

-1,931

0,587

-1,376

0,949

-1,284

3,077

-0,220

0,401

0,649

-0,053

—0,053

0,132

-1,284

3,298

0,016

1,534

-0,244

2,081

-1,568

5,077

1,780

Ш--

Таблица

133

Ь]

О <0

П Я

Контроль

ш>

5»

4 0

—2,071

2,522

1,575

18,453

0,675

—1,152

0,596

2,084

2,110

4,604

7,370

10,171

22,564

4,314

4,604

7,370

10,171

22,563

4,313

-2,0

2,1

—5,937

—9,237

1,929

10,622

6,175

14,542

Оценка точности:

средняя квадратическая ошибка измерения одного угла

Г~йк\ Г 10,45

— у V-

у-т-=

ошибка

1,6/}/~8

0,57",

Таблица

135

Номера

углов

Уравненные

углы

1е

У 1

Номера

углов

Уравненные

угли

у!

1(? З1п

57 00 58,6

59 35 57,9

46 29 48,2

18 00 16,9

—0.0763284

—0.0642366

—0.1394614

—0.5091081

27 22 58,3

3600

05,1

37 54 08,8

7735

46,1

—0.3373043

—0.2307665

—0.2116061

—0.0102576

—0.7899345

274

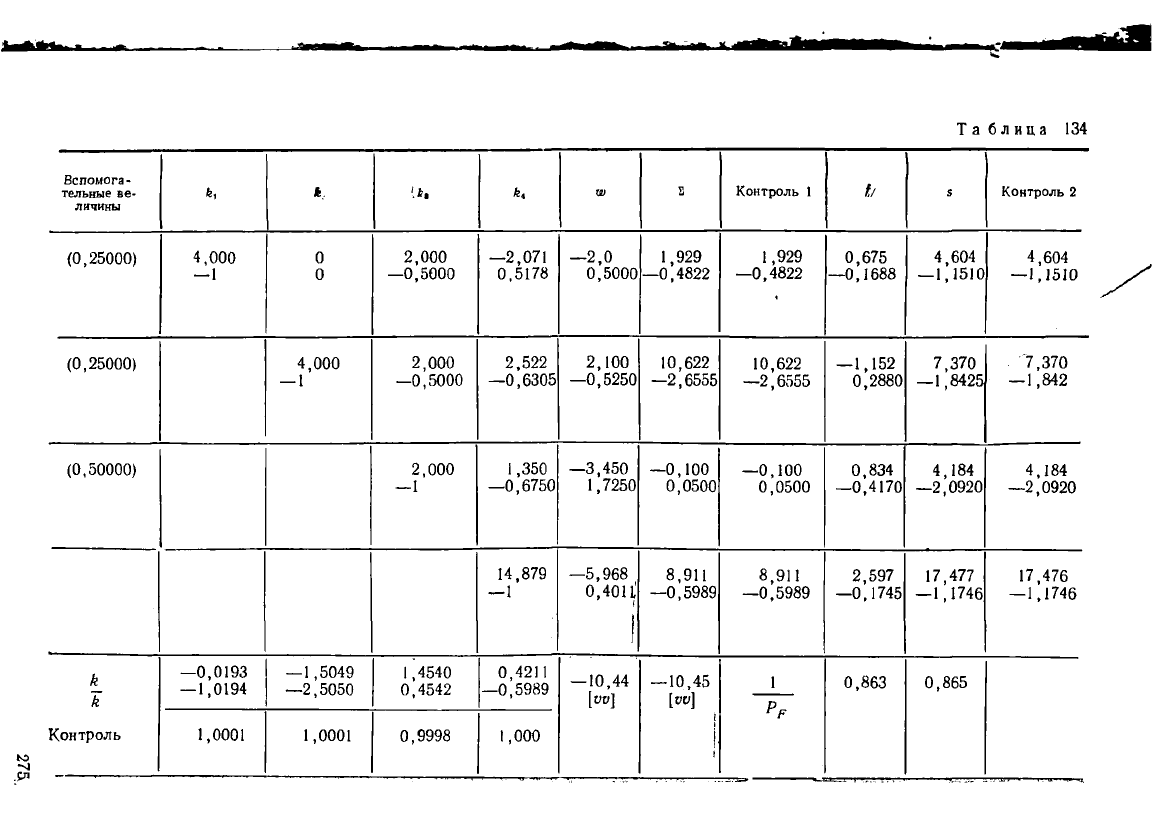
Таблица 129

Вспомога-

тельные

ве-

личины

Контроль

(0,25000) 4,000

— 1

2,000

-0,5000

—2,071

0,5178

-2,0

0,5000

1,929

-0,4822

1,929

—0,4822

0,675

-0,1688

4,604

-1.1510

4,604

—1,1510

(0,25000) 4,000

-1

2,000

-0,5000

2,522

-0,6305

2,100

-0,5250

10,622

—2,6555

10,622

-2,6555

—1,152

0,2880

7,370

-1,8425

7,370

—1,842

(0,50000)

2,000

-1

1,350

-0,6750

—3,450

1,7250

-0,100

0,0500

14,879

—1

-5,968

0,4011;

8,911

-0,5989

—0,100

0,0500

0,834

—0,4170

4,184

-2,0920

4,184

-2,0920

8,911

—0,5989

2,597

—0,1745

17,477

—

1,1746

17,476

-1,1746

Контроль

-VI

.С

—0,0193

1,0194

1,0001

-1,5049

-2,5050

1,4540

0,4542

0,4211

-0,5989

— 10,44

1,0001 0,9998

1,000

-10,45

0,863

0,865

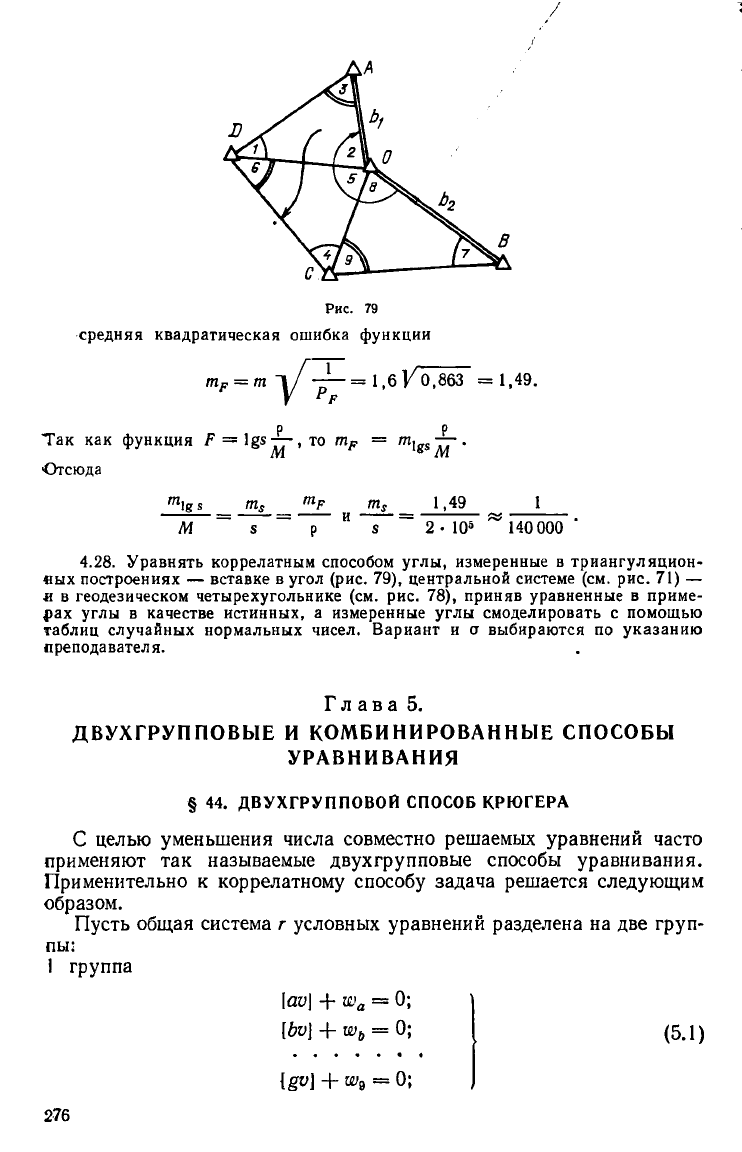
Рис. 79

средняя квадратическая ошибка функции

= т = 1,6 1/0,863 = 1,49.

Р Р

Так как функция Р = —, то т

= т,

. — .

М М

Отсюда

1ез _ Щ _

р т, _ 1,49 1_

М ~ я ~~ р

5 2 - 10

^ 140000 '

4.28. Уравнять коррелатным способом углы, измеренные в триангуляцион-

«ых построениях — вставке в угол (рис. 79), центральной системе (см. рис. 71) —

и в геодезическом четырехугольнике (см. рис. 78), приняв уравненные в приме-

рах углы в качестве истинных, а измеренные углы смоделировать с помощью

таблиц случайных нормальных чисел. Вариант и а выбираются по указанию

преподавателя.

Глава 5.

ДВУХГРУППОВЫЕ И КОМБИНИРОВАННЫЕ СПОСОБЫ

УРАВНИВАНИЯ

§ 44. ДВУХГРУППОВОЙ СПОСОБ КРЮГЕРА

С целью уменьшения числа совместно решаемых уравнений часто

применяют так называемые двухгрупповые способы уравнивания.

Применительно к коррелатному способу задача решается следующим

образом.

Пусть общая система г условных уравнений разделена на две груп-

пы:

I группа

[ао] + о>

= 0;

[Ьо\ + ш

= 0;

+ ^э = о;

(5.1)

276

2 группа

1«|] + иу

= 0;

[Н + щ = 0;

М + ш, =0

(5.2)

с числом г 1 и г

уравнений в каждой. Выполним эквивалентное преоб-

разование системы (5.2) таким образом, чтобы преобразованная сис-

тема

[Ао\ + и>

= 0;

[&>] + т

= 0;

[Си] + = 0,

(5.3)

решаемая совместное (5.1), привела к таким же значениям поправок,

что и совместное решение систем (5.1) и (5.2), и так, чтобы соответст-

вующая (5.1) и (5.3) система нормальных уравнений распалась на две

не связанные общими коррелатами системы (для случая равноточных

измерений):

\аа\ к

+ \аЬ\ к

|аЬ\ к

+ [ЬЬ] к„ +

. + [ад] + =

• + [Ьц\ к

+ ш, = 0,

К + Ш

ь +

. + [я*] К + ТВ. = о

(5.4)

[АА]к

+[АВ\к

\АВ\ к

+ [55] к

. + [АО\к

+и)

= 0,

, + №к

'+т

= 0,

[АО\к

+ [ВО]к

+ . + [00]к

=0.

Очевидно, что для этого необходимо выполнение условия

'[аА\ [аВ] . . . [аО\

ЗУ I [ЬА] [ЬВ] . . . [ЬО\ | _ о,

\1ВА] 1вВ\ №1

(5.5)

(5.6)

т. е. каждый элемент матрицы должен быть равен нулю. Для полу-

чения системы (5.3) согласно правилам эквивалентных преобразований

прибавим к первому уравнению системы (5.2) уравнения (5.1), умно-

женные каждое на вспомогательные множители р

а/

(I = 1, 2, ...,

ко второму — эти же уравнения, умноженные на р^ и т. д., к послед-

нему — умноженные на р^.

В результате несложных действий получим преобразованные коэф-

фициенты

277.

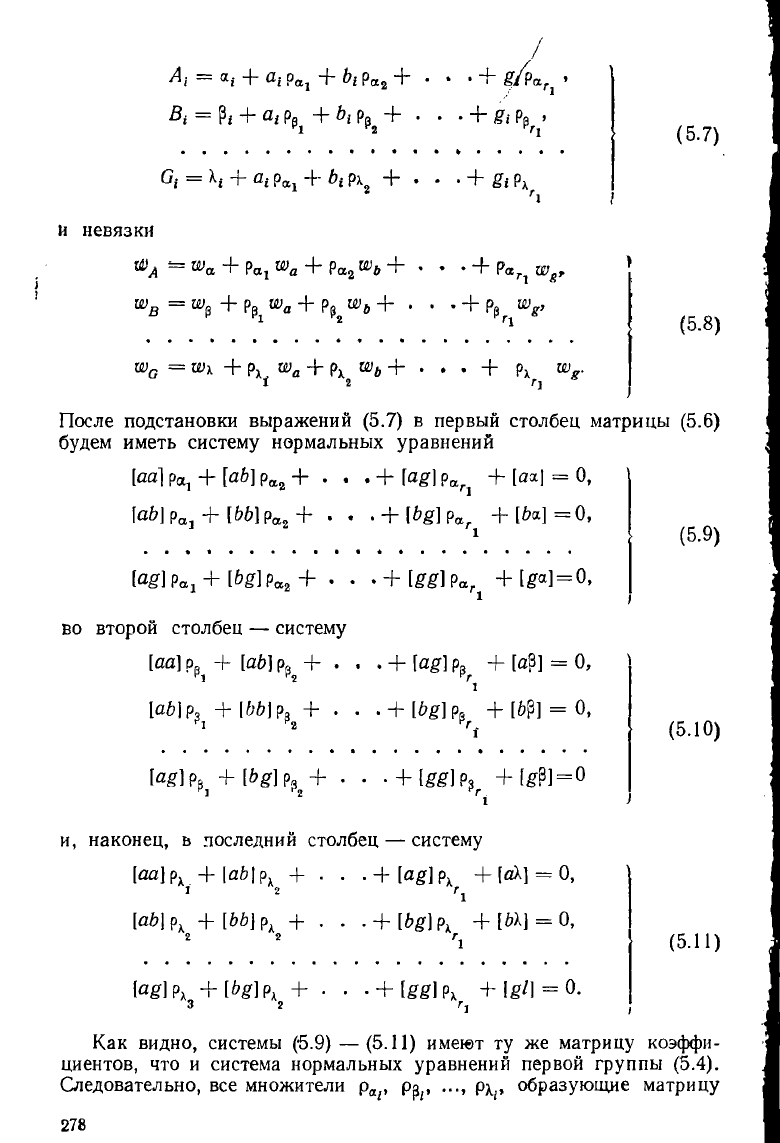
= а, + Ра, + Ь

р«

= р| + а*

Р»

+ Й, Р

+ .

• + й/Ра- •

+ Ра >

о» = +

1 Ра! + Ьг рх

и невязки

Х0

*=О>а + Ра, + Ра

Щ +

ХЮ

=и)

Ъ + Ра + Ря + •

+ ЙРл

• + Р

«V

(5.7)

= шх + р

хю

+ р

хю

{ 2

+ Рх

(5.8)

После подстановки выражений (5.7) в первый столбец матрицы (5.6)

будем иметь систему нормальных уравнений

[И р

Л]

+ [аЬ] р

аг

+ . . . + р

^ + [аа] = О,

\аЬ\

Ра]

+ [ЬЬ] Ра

+ • - • + \Ь§] Р

+ [Ьа\ = О,

[а^1 Р«, + [Ь§]р

а2

+ - • • + [ИГ] Ра

+ [*«] = 0,

(5.9)

во второй столбец — систему

[aa] р^ + [аЬ] + .

[ab]

Р?

+\ЬЬ\ Р

+ .

+ Ш Р

?г

+ [аЗ] = 0,

+ 1Ьд] р

?г

+ №] =

о,

РЙ +\Ь§] Р, + • • - + [ёё}Р

+№ = 0

П '2

и, наконец, в последний столбец — систему

[aa]р

+[аЬ\

Рк

+ . . . + [а^]р

+ [аХ] = 0,

1 2 г

[ab]

Рх

+ [ЬЬ] р

+ . . . + [Ь

]

Рх

+ [Л] = 0,

(5.10)

(5.11)

Как видно, системы (-5.9) — (5.11) имеют ту же матрицу коэффи-

циентов, что и система нормальных уравнений первой группы (5.4).

Следовательно, все множители р

а/

, р^, ..., р^, образующие матрицу

278

Р«1

• • \

Ра

(5.12)

•

размера л

х г

, могут быть вычислены попутно с решением системы

уравнений (5.4), если к ней в схеме Гаусса присоединить дополнитель-

ные столбцы свободных членов

[аа], [ф], . . ., [аХ],

[Ьа], [Ь$], . . [&],

[2®]. [г?]» • •

(5.13)

образующие матрицу Л/

Можно также написать совокупность всех систем (5.9) — (5.11)

в виде

Л^Р + Л/

= 0, (5.14)

где через N1 обозначена матрица коэффициентов уравнений (5.4).

Решая (5.14) путем обращения матрицы Л^, напишем

Р = (5.15)

Если матрицу коэффициентов системы условных уравнений второй

группы (5.2) обозначить через В

, а преобразованной системы (5.3) —

через В

, то вместо (5.7) будем иметь выражение

А = В

г + Р

Хп

1гХп

, (5.16)

г,Хл г

Хп

где В

— матрица коэффициентов условных уравнений группы 1.

Точно так же вектор невязок

= + (5-17)

где вектор = (ш

, т

... щ)

. Вместо (5.16) можно применять

формулу

= В

(Е — Я* Л/7

) = В

Р-

(5.18)

где

Р~

= Е—В

Ы~

В, (5.19)

V' 1 »

V '

согласно (4.51) есть матрица обратных весов предварительно урав-

ненных измерении.

Из независимого решения нормальных уравнений первой и второй

групп находим коррелаты и далее

первичные

I»; =• а,Л

+ + • . • + (5.20)

279.

и вторичные поправки. /

о, = А

+В,к

+ . . . + 0

{

. (5.21)

Величины

у\ = У1+*

{

(5.22)

называют предварительно уравненными измерениями. По этим вели-

чинам можно вычислить преобразованные невязки условных уравне-

ний второй группы ог>А, И>в. и т. д., минуя формулы (5.8) или (5.17).

Общая поправка VI = о* + о^, а величина

[го] = [о'о'] + [о"о"], (5.23)

причем справедливы контрольные формулы

> — = К®а + к

щ + . • • + V*'

_ = к

+ к

хю

+ . . . + к

ы>

Для оценки точности функций при двухгрупповом уравнивании

используется формула рх = [//•/"], которая приобретает вид

/Р~=[РР.г

], (5.24)

где Р

+ а1р

+Ь$

+ . . .+ &Р/ ,

1 2 'г

или Р = [Р~

— преобразованные аналогично (5.7) коэффициенты функции. Из

формулы (5.24) следует, что обратный вес функции вычисляется при

решении нормальных уравнений только второй группы. Вспомога-

тельные множители р^ находят из решения системы уравнений

[aa]

+ [аЬ] р + . . . + [а

\ р + [а/] = О,

1 'г

{

[ab] р +[ЬЬ] р + . . . + [айР, +[Ь/1 = 0,

'1 •'О

Ш Р, + Ш р + . . . + [§§] р + [я/] = о.

При этом справедливо

/[оЛ\

/ [&Л 1

Г-\ ; =0.

Ясно, что средняя квадратическая ошибка одного измерения

280

а функции

~ V ' г

1+г

> '

Ш/г /г

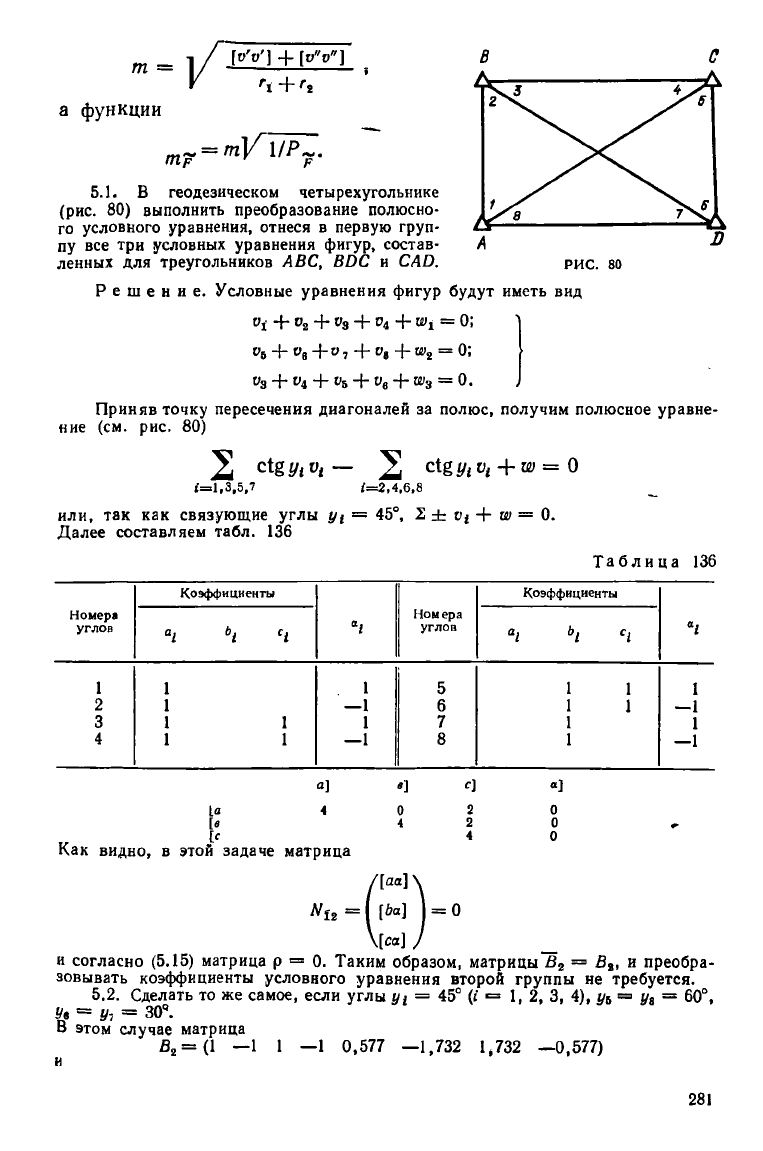
5.1. В геодезическом четырехугольнике

(рис. 80) выполнить преобразование полюсно-

го условного уравнения, отнеся в первую груп-

пу все три условных уравнения фигур, состав-

ленных для треугольников АБС, ВйС и САй. РИС. 80

Решение. Условные уравнения фигур будут иметь вид

+ + ^з + +

ч>1

= 0;

Ч + о

+°7 + + Щ = о;

Vэ-^•V

+ V

+ Щ = 0.

Приняв точку пересечения диагоналей за полюс, получим полюсное уравне-

ние (см. рис. 80)

*=1,3,5,7 /=2,4,6,8

или, так как связующие углы = 45°, 2 ± + т = 0.

Далее составляем табл. 136

Таблица 136

Коэффициенты

Номера

Ном ера

углов

1 Н

углов

1 1 1

1 —1 6

1 1 —1

1 1 1

1 1 —1

—1

Как видно, в этой задаче матрица

N 1

«]

= 0

и согласно (5.15) матрица р = 0. Таким образом, матрицы В

= В,, и преобра-

зовывать коэффициенты условного уравнения второй группы не требуется.

5.2. Сделать то же самое, если углы у

= 45° (< = 1, 2, 3, 4), у

= у

= 60°,

У» ~

У<

— 30°.

В этом случае матрица

= (1 —1 1 —1 0,577 —1,732 1,732 —0,577)

281.

Для матрицы

по способу Ганзена в схеме Гаусса

(0,2500)

(0,500)

(-1)

/ о,;

+о,

\—о,:

0,375

,125

250

+0,125

0,375

—0.250

—0,500

(-1)

—0,260

—дои.

—0,2501

0,500/

вычисляем обратную матрицу Л^ и согласно (5.15) находим матрицу

/ 0,375 0,125 —0,250 \ / 0 \ /—0,289

р = —I 0,125 0,375 —0,250 )•{ —1,155 ) = [ —0,289

\ —0,250 —0,250 0,500 / \ 0 / \ +0,578

и с помощью табл. 137 — матрицу р

и В

по формуле (5.16).

Выполняем контроль:

[аЛ]=0; [М]=0; [сЛ]=0,001.

5.3. В задаче 5.2 выполнить преобразование коэффициентов условных урав-

нений — полюсного и базисного, которое возникает, если в геодезическом четы-

рехугольнике дополнительно измерены базисы А В и АО.

5.4. Применительно к задаче 5.2 с помощью таблиц нормально распреде-

ленных случайных чисел смоделировать измеренные углы с точностью а — 2"

(в качестве истинных значений углов принять ух = 45° ((' = 1, 2, 3, 4), у

= у

—

Таблица 137

Номера

углов

»1 Ч

1 1

—0,289

+0,289

— 1

+0,711

— 1,289

1,289

—0,711

1 1

+0,289

—0,289

0,577

— 1,732

1,732

—0,577

0,866

-1,413

+ 1,443

—0,866

т = (_о, 289 —0,289 +0,578)

282.

Таблица 118

Номера

ходоа

«1

5»

Номера

ходов

«1

«а

11762 10558

8916

9299

11807

9176

10670 9504

10866

5 12334

12404

8382

11868

9020 14303

= 60

и у

= у, = 30°. Выполнить уравнивание углов в группе 1 и в группе 2.

Показать, что формула (5.17) дает такие же значения невязки, какие получатся,

если ее вычислить по уравненным в группе 1 углам.

5.5. Вычислить преобразованные коэффициенты при Ор условных уравнений

координат полигонометрических ходов в задаче 3.53, в которой получены пред-

варительно уравненные дирекционные углы сторон. Измеренные длины сторон

в метрах всех ходов (с учетом их направлений) приведены в табл. 138.

Решение. Так как матрица В = (1 1 ... 1),

а матрица IX"'

[см. (4.66)], то = п',

I Ух Уг • • -Уп'

Р \—Х-} —#2 • • •—Хц'

| (\у] [*]

Поэтому

р = — . , ..

1X2 П \Р"

_ „ \ Лх Чг

• • •

Р" V-

! -6..-.-«„'У

где

[*1 . Ш

п п

— центральные координаты точек хода.

Вычисления на примере хода 1 выполняем в табл. 139.

Таблица 139

Номера

сторон

Дирекцион-

ные углы а

Длины

сторон

Ал^

Ьу

Условные

координаты

1 *1

162°55,0'

185 58,8

156 53,2

11762

10558

8916

—11243

— 10500

—8200

3455

— 1100

3500

0 0

— 11243 3455

—21743 2355

+4489 539

—6011 —561

— 14211 +2939

—29943 5855

= — 15732, 1/

= 2916

283